圆柱形推拉式电磁铁的电磁力数值算法

鲁梦昆,张俊洪,易祥烈*,袁志方

(1.海军工程大学电气工程学院,武汉 430033; 2.湖北工程学院机械工程学院,孝感 432000)

推拉式电磁铁是一种典型的电磁能与机械能能量转换装置,当给线圈中施加励磁电流时,形成的电磁场将使线圈内部软磁性材质的铁芯磁化,在电磁力的作用下,铁芯和推杆会对外输出推力和直线运动。在一些需求短距离直线运动控制的领域,相比于旋转电机及配套运动转换装置结合的方案,螺线管电磁铁装置在制造成本、体积、质量、响应速度等性能方面具有明显优势。鉴于这些特点,推拉式电磁铁被广泛应用于工业自动化领域,包括电磁阀、继电器、电磁振动器等多种形式,在各种应用种准确的电磁力控制都是至关重要的[1-2]。

推拉式电磁铁作为一项基础应用技术一直以来都是中外科研工作者的重点研究方向[3]。近些年随着工业科技的发展和对电能源应用的愈发重视,螺线管电磁铁相继出现了一些新的应用方式。其中包括文献[4]中介绍的一种电磁铆接机,主要功能是为大飞机的蒙皮外壳板材进行铆钉铆接;文献[5]中介绍的一种电磁卷边机;文献[6]中分析了一种直线柱塞泵,液压动力直接通过施加在活塞上的电磁力得到,而不是由旋转动力转换而来,更适用于小型、结构紧凑的工作环境;相比于化学能,电能在太空中具有可再生的优势,是卫星运行的主要动力源,推拉式电磁铁体积小的特点非常适合在太空中应用[7],如文献[8]中介绍了一种小型卫星的太空对接方案,文献[9]中提出了一种基于单线圈铁芯螺线管的立方体纳卫星微型电磁对接硬件重构设计方案。虽然推拉式电磁铁应用广泛,但因为铁芯是活动的,电磁力、磁芯位置、电流等电磁数据之间存在强非线性关系,解析计算非常困难[10-11],在工程应用中的动态性能难以准确控制。

在推拉式电磁铁电磁场计算模型的研究方面,无铁芯的螺线管磁场容易根据Biot-Savart定律计算,而含铁芯的螺线管线圈则计算过程较为复杂,成熟的理论成果较少,目前可用的方法包括半解析计算法和有限元法(finite element method,FEM)、其中半解析法包括集总参数磁路模型法和磁场子域方程法[12]。有限元法计算存在计算速度慢,变量之间对应关系不清晰的问题[13];集总参数磁路模型法主要用以计算磁场的平均值,而不是一个区域的详细分布,因而计算准确度不高[14];文献[15-16]中从理论层面解释了子域磁矢量方程计算铁芯螺线管的磁感应强度、电感、电磁力的过程。

基于子域磁矢量方程的数值算法相比于有限元法具有计算速度快、可程序化等优点,能完成一些有限元不能直接处理的计算任务。现利用数值算法分析一种不带铁磁性外壳的推拉式电磁铁,含特殊函数的磁矢量势方程通过MATLAB编程计算数值解,在计算得到电感和电磁力后对比有限元仿真结果和实验结果说明该方法的计算准确度。

1 电磁力数值算法建模

推拉式电磁铁主要由励磁线圈、软磁性材质的铁芯和弹簧组成。其中弹簧的作用主要是使铁芯具有复位功能,弹簧力的方向与电磁力方向相反。当线圈中通以任意方向的励磁电流时,铁芯受到电磁力的作用并产生向线圈中心移动的趋势。推拉式电磁铁的结构图如图1所示。

图1 推拉式电磁铁的结构图

由于铁芯顶端的圆环结构不会进入线圈,距离线圈较远,下方的推杆为渗碳无磁不锈钢材质,因此可将推拉式电磁铁的铁芯和线圈视为标准圆柱体进行分析。

1.1 磁矢量势方程

磁场子域磁矢量势方程的数学模型中假设了铁芯的磁导率无穷大,铁芯上的磁力线均垂直于铁芯表面[17],即铁芯边界处的磁感应强度切向分量为零。以铁芯的中轴线为中心线建立柱状旋转坐标系,以求解域圆柱体的3个面为外部边界条件,推拉式电磁铁磁场子域划分及各边界条件如图2所示。

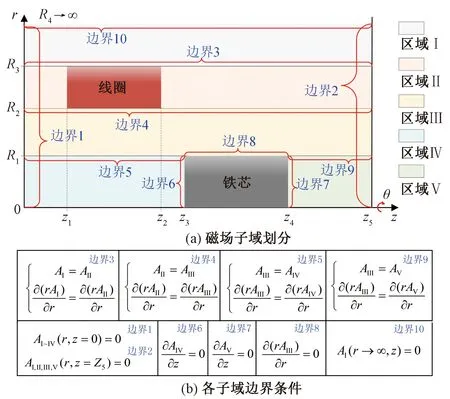
z为螺线管的轴向方向;r为螺线管的径向方向;R1为铁芯半径;R2为线圈内半径;R3为线圈外半径;R4为求解域半径;Z1为线圈的左边界;Z2为线圈的右边界;Z3为铁芯的左边界;Z4为铁芯的右边界;Z5为求解域长度;AⅠ、AⅡ、AⅢ、AⅣ、AⅤ分别为5个区域的磁矢量势

为了使求解结果更准确,各边界应远离线圈和铁芯。由麦克斯韦方程可知

-∇B=∇2A=-μ0J

(1)

式(1)中:∇为倒数算符;B为磁感应强度;A为磁矢量势;μ0为空气中的磁导率,取4π×10-7H/m;J为线圈中的电流密度。

注意磁场呈圆柱状具有旋转对称性,磁矢量势仅有周向θ方向的分量,其大小与r、z的坐标相关,可表示为

(2)

柱状坐标系下螺线管磁感应强度的3个分量[17]分别为

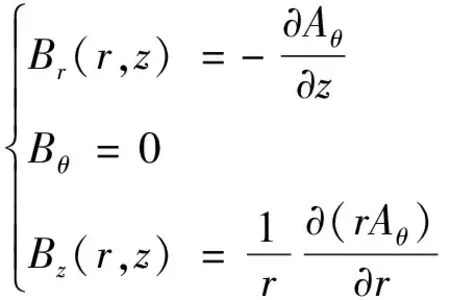
(3)

联立式(1)～式(3)得到磁矢量势方程满足

(4)

式(4)中:Aθ=A(r,z);电流密度J表示为与坐标点相关的函数J(r,z),以便区分电流密度为零的空气区域。

利用分离变量法求解齐次微分方程,可得磁矢量势的通解为

(5)

式(5)中:c1～c4为待定常数;I1为第一类一阶虚宗量Bessel函数;K1为第二类一阶虚宗量Bessel函数[18](也被称为第二类一阶修正的Bessel函数);n为级数解的谐波项数;αn为与级数相关的系数。

根据圆柱坐标系的磁矢量势在外部边界处I1和K1的敛散性可分别得到简化后的各子区域磁矢量势通解形式为

(6)

式(6)中:

(7)

根据线圈的电感储能和磁矢量势的关系,即

(8)

式(8)中:Lm为带铁芯的电感;I为线圈中的电流;V为导体的体积。

可推导出电感的计算式,设线圈中的电流均匀分布于线圈的矩形截面上,即电流密度为电流除以矩形截面的面积,推导出含铁芯的电感为

(9)

式(9)中:

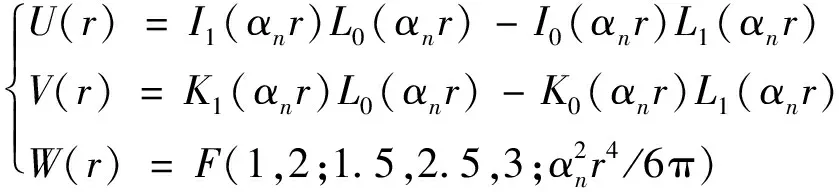
(10)

式(10)中:L为线圈长度;N为线圈匝数;F为超几何函数。

由式(9)和式(10)可知,当线圈和铁芯结构尺寸已知时,只要知晓铁芯与线圈的相对位置和励磁电流即可通过子域磁矢量势方程求得对应的电感值。

1.2 电磁力方程

在得到电感曲线后,可通过电感梯度变化计算铁芯受到的电磁力。使用虚拟位移法求解运动学过程,即

(11)

式(11)中:W为磁感应能;L(x)为与可动铁芯位置x(t)有关的电感值;i(t)为线圈的励磁电流。

铁芯在线圈轴向上受到的电磁力为

(12)

实际上得到电磁力曲线的同时,也容易计算出铁芯的加速度和速度,铁芯的运动方程为

(13)

式(13)中:m为铁芯的质量;x(0)为弹丸与线圈的初始相对位置。

由电磁力方程可知,在得到电感的情况下可计算铁芯的运动状态,因而可用于控制电磁阀阀芯[20]。不限制铁芯的运动时,可将电磁铁视为磁阻型电磁加速器,可根据电流和电感梯度的变化计算出铁芯的运动过程,也能根据电感的变化逆向计算电流,形成电磁加速过程的动态闭环计算[21]。

2 数值计算模型的仿真验证

为了验证电感计算的准确性,构建如图1所示的推拉式电磁铁的ANSOFT/Maxwell有限元仿真模型,同时编写MATLAB数值计算程序,电磁铁的各结构参数如表1所示。

表1 圆柱形推拉式电磁铁的建模参数

2.1 磁矢量势对比分析

从图1可知,推拉式电磁铁铁芯下移8.2 mm时,铁芯和线圈的相对位置为-17.3 mm。根据式(6)使用MATLAB编程求解到各子域磁矢量势方程的7个未知积分常数后,可绘制磁矢量势分布图。当给定线圈中的励磁电流为4 A时,子域法计算的磁矢量势分布图与有限元结果对比如图3所示,其中有限元中铁芯的磁导率分别设置为电工软铁的B-H曲线和定值10 000进行仿真。

图3 FEM与子域法计算的磁矢量势的对比

当励磁电流为4 A时,3个磁矢量势峰值数据分别为3.608 8×10-3、3.585 6×10-3和3.599 4×10-3Wb/m,相差较小。实际上励磁电流的大小与磁饱和程度必然相关,为了具体分析磁矢量势的计算准确度,给线圈施加不同大小的励磁电流,对比有限元的分析结果如图4所示。

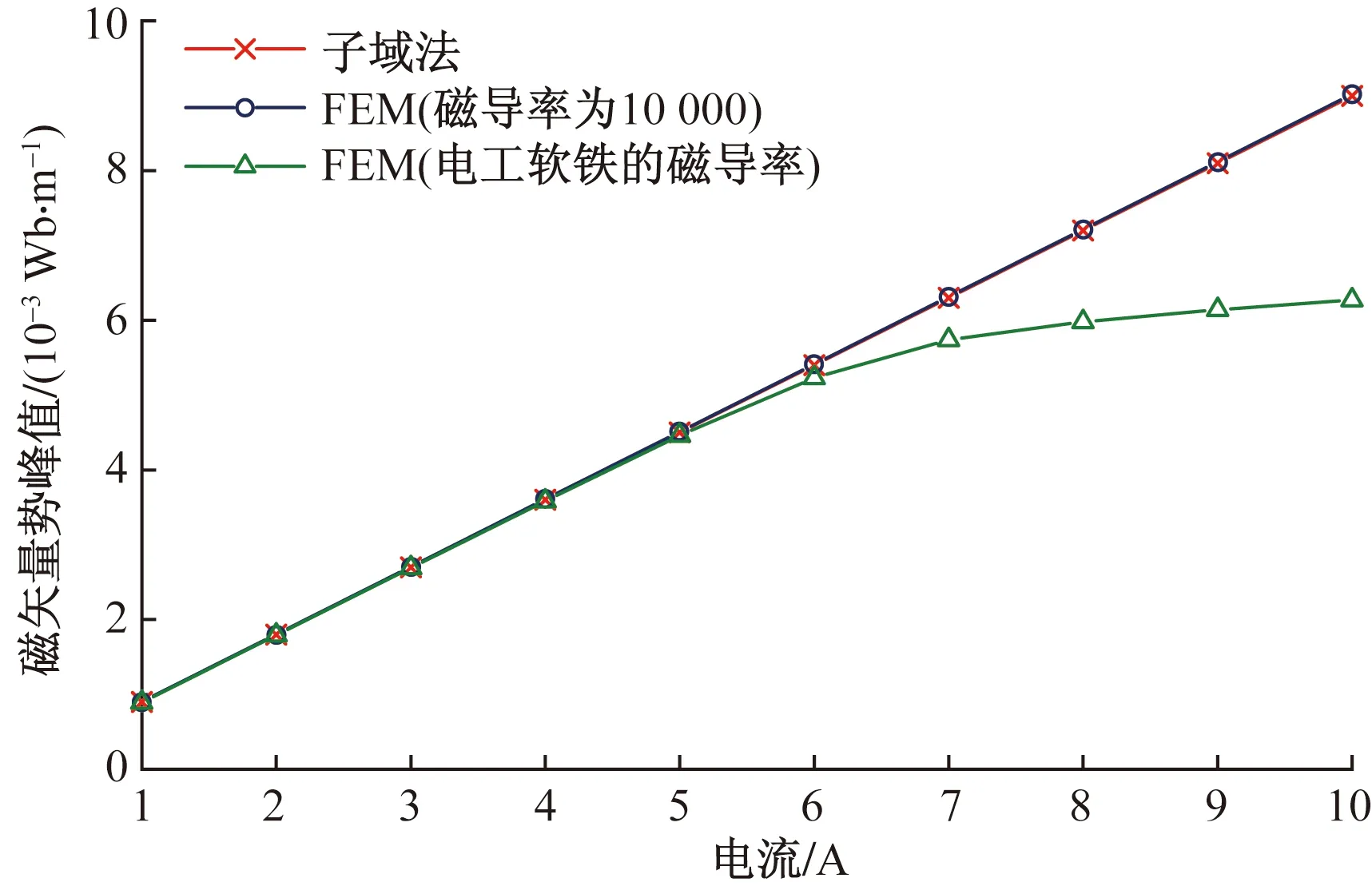
图4 磁矢量势峰值对比

由图4可知,随着电流的增加,有限元中磁导率设置为10 000时和子域法计算的磁矢量势峰值基本相等,这对应了子域磁矢量势方程建立时铁芯磁导率为无穷大的假设,说明数值算法的计算结果非常近似地等于有限元中磁芯磁导率设置很大的情况。而当有限元中铁芯材质设置为电工软铁计算的磁矢量势峰值不会线性增加,而是按照B-H曲线的趋势增加,磁芯磁饱和程度逐渐加大。由此可以判断电磁铁铁芯下移8.2 mm时,想要子域磁矢量势方程计算结果具有较准确的计算结果,线圈中的电流不宜超过6 A。

子域磁矢量势方程计算较准确的电流阈值必然与铁芯的位置相关,可在推拉式电磁铁的铁芯工作行程内确定,以便明确该数值算法能准确计算电磁力的使用条件。

2.2 电感对比分析

研究中可通过电感曲线计算电磁力曲线,直接分析不同励磁电流情况下子域磁矢量势方程计算电磁力的准确度。由于子域磁矢量势方程中磁导率为无穷大时,电感不会随励磁电流变化,计算电感曲线全部重合。因此重点对比铁芯工作行程内电工软铁材质铁芯的电感曲线即可知晓电感计算准确度。铁芯在线圈中心线上每移动0.5 mm取1个数据点,电感曲线对比如图5所示。

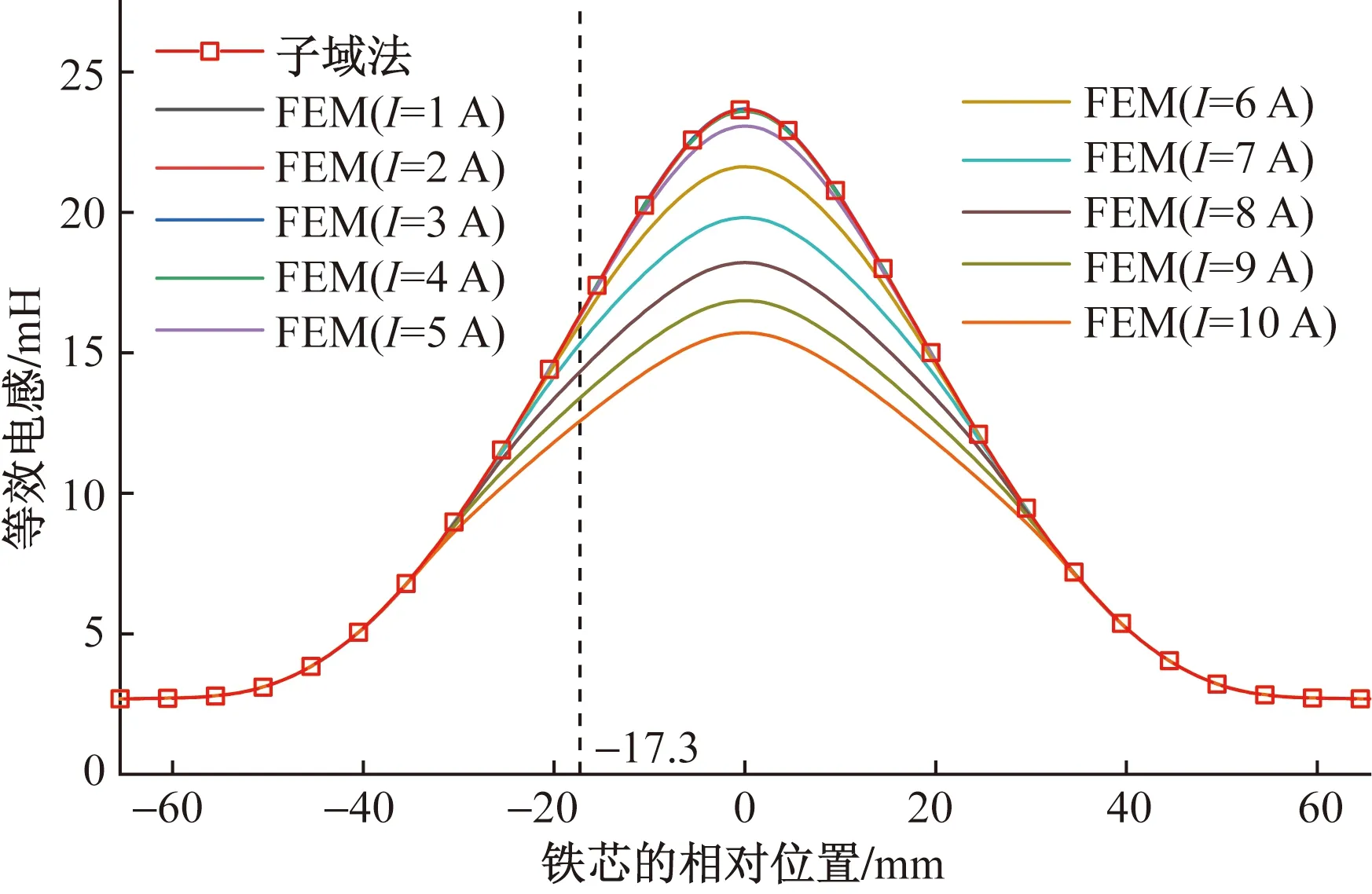
图5 不同励磁电流时的等效电感曲线对比

由图5可知,当电流为1～4 A时,无论铁芯在任何位置,各电感曲线高度重合,可以推断此阶段铁芯未发生磁饱和。当电流达到5 A时,仅当铁芯中心在线圈中心的-10～10 mm区域内有所偏差,且铁芯与线圈相对位置越近误差越大。铁芯在-17.3 mm 位置时,励磁电流为6 A时磁芯发生了轻微的磁饱,但误差只有2.085%,可以认为该电流值即为子域磁矢量势方程计算推拉式电磁铁电感较准确的阈值。

2.3 电磁力对比分析

得到电感曲线后可根据式(12)计算电磁力,与有限元中磁芯为电工软铁的仿真结果对比如图6所示,由于有限元中默认z轴向上方向为正,所以铁芯向下移动过程中电磁力为先负后正。

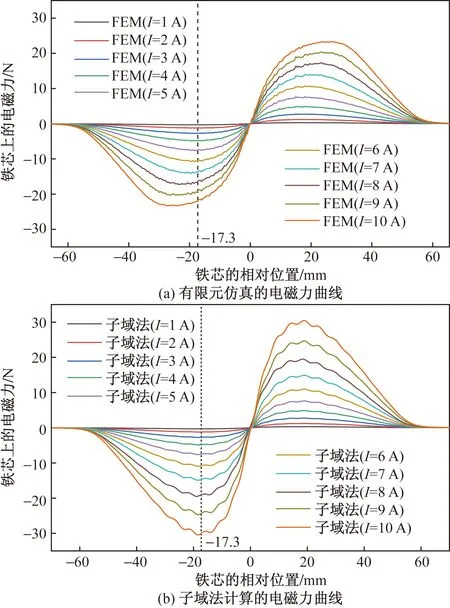
图6 不同励磁电流时的电磁力曲线对比

从图6(b)中可以看出,数值算法计算的电磁力曲线呈波浪状,这符合磁矢量势方程谐波次数和函数的特征。推拉式电磁铁铁芯相对位置-17.3 mm时,有限元和子域法的电磁力对比及和相对误差如图7所示,为了方便与实验中力传感器受到的压力作对比,电磁力以向下方向为正。

图7 电磁力对比

由图7可知,当电流为1～5 A时,数值算法计算的电磁力相比于考虑铁芯材质B-H曲线的有限元结果相差不超过3%,当电流为6 A时的计算偏差约为5%,继续增大电流将导致误差迅速增加。

3 数值计算模型的实验验证

3.1 实验平台搭建

为了验证磁场子域磁矢量势方程数值算法计算推拉式电磁铁电磁力的准确程度,搭建了如图8所示的电磁力测试实验平台,在实验过程中拆卸弹簧以剔除弹簧力的影响。为了获得准确的测试效果,测试过程中应当确保铁芯相对于线圈不会在电磁力作用下发生位移,力传感器应当有足够的安装预紧力。在钢质安装架与螺线管之间装夹木垫可尽量避免安装架的铁磁性对螺线管磁场产生影响。此研究中的实验平台布置为纵向,可有效减少摩擦力和磁芯偏心等问题给计算带来的误差,使分析更准确。为了避免力传感器自身的重力和安装预紧力对测试结果带来误差,测试前先对变送器调零,该操作也同时剔除了铁芯的重力。

图8 电磁力测试实验平台

3.2 数据对比分析

实验过程中利用可调直流电源给线圈施加1～8 A不同大小的直流电(螺线管的额定工作电流约7.2 A),电流数据通过直流电流传感器检测,力传感器检测的电压与力转换比为10 N/V。示波器中采集到的电流和电磁力与有限元仿真和子域法计算结果对比如表2所示,其中有限元和MATLAB程序中的电流激励按照实验中实测电流给定。另外,图9中显示了励磁电流分别为约为2.982 A和6.997 A两种情况的示波器波形。

表2 仿真、计算及实验获得的电磁力对比

当电流较小时,传感器等本身的误差相对较大,因而不适合以该数据结果为标准分析基于子域磁矢量势方程的半解析数值算法的误差。有限元中分析模型则过于理想化,以实验结果为标准分析误差更合理。实验中当电流为2～5 A时,数值算法计算误差不超过3%,当电流约为6 A时误差约为7.25%,随着电流继续增大数值算法的误差迅速增加。因此判断数值算法的适用电流阈值应不高于 5～6 A,在此条件下数值算法的计算结果具有可信度。

4 结论

推拉式电磁铁具有结构简单、制造成本低、体积小、响应速度快等优点,虽然其已被广泛应用于各行各业,但由于磁场的非线性变化,解析计算困难,现阶段的计算基本上都是靠有限元来处理。与有限元法相比,基于数学方程的半解析法具有计算过程清晰、可程序化、算法编辑灵活等优点,可实现一些有限元无法处理的计算,是理论与应用研究的发展趋势。

研究了柱状坐标系下的磁场子域方程,通过MATLAB编程实现了一种推拉式电磁铁电磁特性数据的计算,包括磁矢量势、电感和电磁力等。数值算法计算的结果与有限元中设置铁芯磁导率为10 000时的结果高度重合,但当铁芯线设置为电工软铁的B-H曲线时,随着电流的加大铁芯会发生磁饱和。当磁饱和问题不严重时,数值算法的计算结果具有高准确度,可等效于有限元法;随着电流的增加,发生磁饱和后误差迅速增加。在实际使用时,可对比空载情况下有限元计算的磁矢量势或电感,提前获取电流大小与误差的变化规律,明确数值算法计算较准确的电流阈值,以此避免磁饱和导致计算误差过大的问题。

经过研究,基于子域磁矢量势方程的半解析数值算法的主要缺点包括:仅适用于标准圆柱状的含铁芯或空心螺线管;磁芯磁导率太低或发生磁饱和后计算准确度降低。在后续的研究中有必要研究可动铁芯动态电流情况下磁饱和修正算法。