基于等效源法的单全息面声场分离机理及技术
2023-11-23伍松郑贤赵鑫李常虎
伍松,郑贤,赵鑫,李常虎
(1.广西科技大学机械与汽车工程学院,柳州 545006; 2.广西汽车零部件与整车技术重点实验室(广西科技大学),柳州 545006)
近场声全息(near field acoustic holography,NAH)技术[1-2]突破了早期声全息的瑞利分辨率限制,是一种空间高分辨率的噪声识别和定位技术,在声场可视化和重建方面有着巨大的技术优势和广泛的应用前景。以靠近声源全息面上声压或质点振速等声学量作为输入,通过全息算法便可重建整个三维空间任一点处的所有声学量。然而,当空间有多个声源时,全息面测量所获得的声学量为多个声源的叠加,以该声学量作为输入来进行声源的识别和声场的重建,将会带来巨大的误差。近场声全息技术要求测量时所有声源位于全息面一侧,另一侧声场为自由场,工程测量中,难以满足这一条件,限制了近场声全息技术的应用。
如何将目标声源信息从复杂声场中提取出来,成为声源定位[3]和声场重建[4]的关键。声场分离技术能够很好地解决有多个相干声源位于测量面两侧的问题。根据声场分离的原理,声场分离方法可以分为基于空间Fourier变换法[5-7]、边界元法[8]、统计最优法[9-10]、波叠加法[11-13]和等效源法(equivalent source method,ESM)[14]等分离方法。在这些声场分离方法的基础上,根据全息面的数量,分为单全息面声场分离和双全息面声场分离方法。根据输入的全息面参数,可以分为基于声压-振速(p-u)的单全息面声场分离、基于声压(p-p)的双全息面声场分离以及基于振速(u-u)的双全息面声场分离。上述分离方法以两个全息面的声压或振速,或者一个全息面上的声压和振速作为声学量输入。采用双全息面声场分离方法,采样点数目较多,且精度不高。两个全息面距离的选择没有通用准则,只能依靠经验进行选择,如果参数选择不当,会产生较大的分离误差。最近,文献[15-17]利用误差原理,推导出单全息面声场分离方法。文献[18]利用单层传声器阵列一次获得两个全息面的声压实现声场分离。文献[19-20]运用重采样原理,建立起每个源对每组声源的声压贡献与源强之间的关系,计算出声源源强后,实现声场分离。
综上所述,双全息面声场分离技术的两个测量面之间的间距对分离精度影响较大,而且只能凭借经验进行间距的选择。单全息面声场分离技术与之相比,避免了测量面之间距离对分离精度的影响。现有的单全息面声场分离技术,需要一定的先验知识,现提出一种无需先验知识便可实现多源相干声场分离的方法。该方法首先运用基于空间变换的近场声全息,根据测得的全息面声压重建出源面的位置,实现对声源的定位。然后利用等效源法,建立起全息面上声压测量值和法向振速测量值与目标声源单独对全息面贡献的声压和法向振速之间的关系,从而直接实现对目标源的声压和法向振速分离,并通过数值仿真证明其可行性。
1 理论研究
1.1 近场声全息原理
对于Z>0的正半空间为自由声场的情况,假设全息面Z=ZH,重建面Z=ZS,则近场声全息的重建公式[21-22]为
p(kx,ky,ZS)=p(kx,ky,ZH)exp[-ikz(ZH-ZS)]
(1)
v(kx,ky,ZS)=kzp(kx,ky,ZH)exp[-ikz(ZH-ZS)]/ρck
(2)
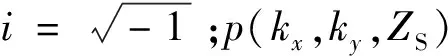
1.2 等效源法近场声全息
ESM的基本原理是振动体辐射的声场可由其内部或表面布置的一系列等效源点产生的声场叠加来代替。声场中任意场点处的压力p和振速v可表示为
(3)
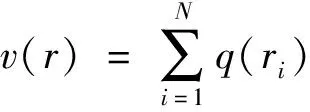
(4)
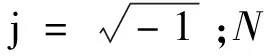
(5)
假设采用M个麦克风阵列来测量全息面上的声压和法向振速,这时全息面上的声压和法向振速可以表示为矩阵的形式,其简化为
PH=GHQ
(6)
VH=DHQ
(7)
式中:PH为M×1维矩阵;GH为M×N维矩阵,表示等效源点到全息测量面的声压传递矩阵,且GH(r)=iρωg(r,ri);Q为N×1维矩阵,表示等效源点产生的源强;VH为M×1维矩阵;DH为M×N维矩阵,表示等效源点到全息测量面的振速传递矩阵,且DH(r)=∇ng(r,ri)。
根据式(6)和式(7)可以得到未知的源强向量。
(8)
(9)
式中:上标“+”表示矩阵的广义逆,当M≥N时,即全息面上使用的测点数量不少于等效源点数时,此时Q可由最小二乘法求得最优解,可表示为
(10)
(11)
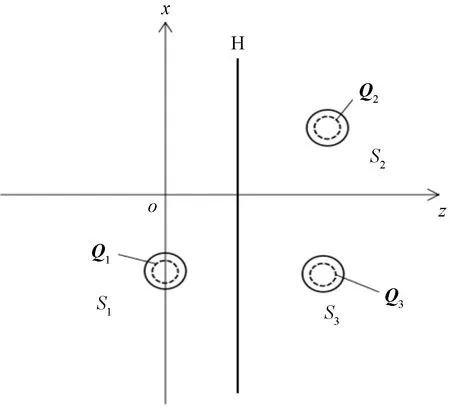
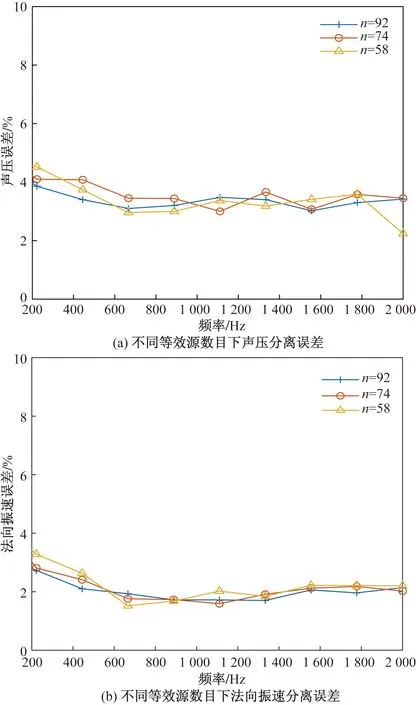
当M (12) (13) 式中:上标“H”表示矩阵的共轭转置;I为单位矩阵;λ为正则化系数,可按照统计最优近场声全息中的方法获取[23]。 求出等效源点的声源强度后,根据式(6)和式(7)便可重建声场中任意点处的声压和法向振速,即 PR=GRQ (14) VR=DRQ (15) 在测得全息面的声压后,通过式(1)或式(2)重建声源面,并在声源面上找出声压和法向振速的极大值点,将其确定为声源位置[22]。 如图1所示,全息面上所测得的声学量是两侧声源共同作用的结果,根据叠加原理,全息面上的声压和法向振速可表示为 H为全息面;S1、S2为声源 P=P1+P2 (16) V=V1-V2 (17) 式中:Pi为第i个声源在全息面上产生的声压;Vi为第i个声源在全息面上产生的法向振速。其中每个声源单独产生的声压和法向振速可以表示为 P1=G1Q1 (18) P2=G2Q2 (19) V1=D1Q1 (20) V2=D2Q2 (21) 对式(18)~式(21)进行求逆,便可得到用声压和法向振速表示的声源源强。 (22) (23) (24) (25) 对求逆过程进行正则化,可以得到 (26) (27) (28) (29) 将式(17)、式(22)、式(25)代入式(16)可得分离后目标声源的声压为 (30) 同理将式(16)、式(23)、式(24)代入式(17)可得分离后目标声源的法向振速为 (31) 式(30)和式(31)为存在两个相干声源时基于等效源法单全息面的的声场分离公式,当得到全息面上的声压测量值和法向振速测量值,运用声场分离公式,便可以直接分离出目标声源单独辐射的声压和质点法向振速。 在图1的基础上,添加一个干扰源,即声场中有3个声源:声源1为目标源;声源2和声源3均为干扰源。如图2所示,全息面的测量声压和法向振速为3个声源共同作用的结果,根据叠加定理,全息面的声压和法向振速表示为 图2 两个干扰源时的声场位置示意图 P=P1+P2+P3 (32) V=V1-V2-V3 (33) 式中:P3=G3Q3,V3=D3Q3。由于声源2和声源3均为干扰源,两个声源辐射的声压和法向振速表示为 (34) (35) 式(32)和式(33)可表示为 P=P1+P23 (36) V=V1-V23 (37) 对式(34)和式(35)进行求逆,可得到声源2和声源3共同作用产生的源强 (38) (39) 将式(20)、式(37)、式(39)代入式(36),可得到3个声源时,分离得到的目标源声压分离值。 (40) 同理将式(18)、式(36)、式(38)代入式(37),可得到3个声源时,分离得到的目标声源法向振速分离值。 (41) 将其推广到多个干扰源的声场,假设声场中存在i(i=1,2,…,n)个声源,目标源的声压分离值和法向振速分离值可以表示为 (42) (43) 为了验证基于等效源法单全息面声场分离方法的可行性,对其进行了数值仿真实验。如图2所示,在全息面H两侧布置两个脉动球作为声源,声源S1作为目标源,其坐标位置为(-0.15,0,0) m,声源S2作为干扰源,其坐标位置为(0.15,0,0.2) m。脉动球半径均为0.01 m,表面振速均为0.25 m/s。传播介质为空气,其密度取1.21 kg/m3,声音在空气中的传播速度为c=341 m/s。测量面位于ZH=0.08 m测点位于大小为0.4 m×0.4 m,网格间距为0.08 m的测量面节点处。为了使仿真结果更加接近真实测量结果,仿真中,在全息面上加入了信噪比SNR=30 dB的高斯白噪声。为了定量地分析分离精度,这里给出了分离声压和分离法向振速的误差为 (44) (45) 式中:Ep为声压的分离误差;Pth为声压理论值;Pcal为声压分离值;Ev为质点振速的分离误差;Vth为法向振速理论值;Vcal为法向振速分离值。 在频率为1 000 Hz时按照上述条件运用MATLAB进行了数值仿真,图3(a)和图3(b)分别全息面上的声压测量值和法向振速测量值。图4(a)和图4(b)分别为目标声源(声源S1)辐射到全息面上的声压理论值和法向振速理论值。从图3(a)和图4(a)的对比可以看出,目标源的声压理论值与全息面上的声压测量值存在巨大的差异,声压测量值不能准确反映目标源在全息面上的辐射声压。从图3(b)和图4(b)的对比也能看出目标源产生的法向振速理论值与全息面上的法向振速测量值存在巨大的差异,法向振速测量值不能真实反映目标源在全息面上辐射的法向振速。说明了存在干扰源的情况下,全息面上声压和法向振速的测量值与目标源声压和法向振速的理论值存在巨大差异,不能准确反映目标源在全息面上辐射的真实信息,若直接使用声压和振速的测量值重建声场,将会影响重建精度,甚至导致重建失效,需要对其进行声场分离的预处理。图5(a)和图5(b)分别为使用本文提出的分离方法获得的目标源声压分离值和法向振速分离值。从图4(a)和图5(a)的对比可以看出,所提方法得到的声压分离值与目标源声压理论值具有较好的吻合,验证了所提方法能实现声压的有效分离。根据计算结果,相干声源声压分离的误差仅为2.74%。从图4(b)和图5(b)的对比可以看出所提方法得到的法向振速分离值与目标源产生的法向振速理论值具有较好的吻合,验证了所提方法能实现法向振速的有效分离。根据计算结果,相干声源的法向振速分离误差为1.77%。通过图4和图5的对比,说明了本文提出的方法能有效实现声压和法向振速的有效分离。 图3 全息面上测量得到的声压和质点法向振速 图4 目标源在全息面上产生的声压和质点法向振速的理论分布 图5 采用本文提出的方法得到的声压和质点法向振速的分离值分布 图6(a)和图6(b)分别为声压测量值和目标源产生的声压理论值以及本文方法得到的声压分离值实部和虚部对比图。从图6中可以看出声压测量值的实部和虚部与声压理论值的实部和虚部不一致,说明了当存在干扰源时,声压测量值并非由目标源单独辐射产生的,是多个声源共同作用的效果。同时也能看出声压理论值和声压分离值的实部和虚部都具有较好的吻合,再次验证了所提方法能实现声场声压的有效分离。 图6 两个声源时全息面上的声压结果比较 图7(a)和图7(b)分别为法向振速测量值和目标源产生的法向振速理论值以及采用所提方法得到的法向振速分离值的实部和虚部对比图。从图7(a)和图7(b)中可以看出法向振速测量值的实部和虚部与法向振速理论值不一致,说明了在有干扰源存在的情况下,法向振速测量值并非有目标源单独辐射产生的。同时可以看出法向振速理论值的实部和虚部与所提方法分离得到的法向振速分离值具有较好的吻合,再次验证了所提方法在 能实现声场法向振速的有效分离。 为了进一步研究不同影响因素对声场分离效果的影响,对不同信噪比和不同等效源数目下的声场分离进行分析。图8为不同信噪比下所提方法的声场分离误差对比图。图8(a)为不同信噪比下的声压分离误差,可以看出:SNR=30 dB时,在整个频率范围内,声压分离误差低于5%,分离误差很小;SNR=25 dB时,在整个频率范围内,声压分离误差在5%~8%,仍然具有较好的分离精度;当SNR=20 dB和SNR=15 dB时,声场的声压分离精度相对于SNR=30 dB差了很多。说明该方法分离声压受到信噪比的影响,当信噪比低于20 dB,声场声压的分离精度较差。图8(b)为不同信噪比下的法向振速分离误差,从图8(b)中可以看出SNR=30 dB时,在整个频率范围内,法向振速的分离误差低于5%,具有良好的分离精度;SNR=25 dB时,法向振速的分离误差3%~6%,仍然具有较好的分离精度,且分离误差比较稳定;当SNR=20 dB和SNR=15 dB时,法向振速的分离效果明显比SNR=30 dB时差了很多,且容易受到频率变化的影响。说明了该方法在分离法向振速是,同样受到信噪比的影响,且信噪比在高于25 dB时,分离效果更好。 图8 信噪比对分离误差的影响 本文等效源点布置在脉动球内部并位于与其共中心的球面网格结点上,结点按经纬度等网格划分。图9为等效源个数对声场分离误差影响的对比图,图9(a)为不同等效源个数下的声压分离误差图,从图9中可以看出:当n=92、n=74和n=58时,在整个频率范围内,声压分离误差走势基本相同,且都具有较高的分离精度,说明了本文提出的方法在分离声压时受等效源个数影响不明显。图9(b)为不同等效源个数下的法向振速分离误差图,从图9(b)中可以看出,在不同等效源数目下,法向振速分离误差均低于4%,具有较高的分离精度,没有受到等效源个数的影响,说明了该方法受等效源个数的影响不明显。 图9 等效源点个数对分离误差的影响 在2.1节的基础上添加一个声源S3作为干扰源,其坐标位置为(-0.15,0,0.2) m,如图2所示。图10(a)和图10(b)分别为全息面的声压测量值、目标源产生的声压理论值以及使用本文所提方法得到声压分离值的实部和虚部对比图。从图10(a)和图10(b)中可以看出:声压测量值的实部和虚部与声压理论值的实部和虚部都存在较大的差异,声压理论值的实部和虚部与声压分离值的实部和虚部均具有较好的吻合结果。说明了该方法在有两个干扰源的情况下,能实现声压的有效分离。根据计算结果,相干声源的声压分离误差仅为4.34%。图11为3个声源时,法向振速测量值、目标源产生的法向振速理论值以及使用本文方法得到的法向振速分离值的实部和虚部对比图。从图11可以看出,法向振速测量值与法向振速理论值存在差异,法向振速分离值与法向振速理论值具有较好的吻合结果。说明了当有两个干扰源时,提出的方法仍然可以将目标源的声压和法向振速从声场中分离出来。验证了该方法在有多个干扰源时仍能精确地分离声压和质点振速。且根据计算结果,相干声源的法向振速分离误差为3.74%。说明了本文提出的方法不仅能实现两个声源时的有效分离,且能推广到多个声源时的声场分离。 图11 3个声源时全息面上的质点法向振速 对单全息面声场分离技术做进一步研究。利用源强建立起声压和法向振速的关系,运用叠加原理,推导出全息面上的声压测量值和振速测量值与声源辐射信息之间的关系,实现了声场分离,并将其推广到多个声源的声场分离。通过数值仿真进行验证,得出如下结论。 (1)通过测量声压(法向振速)、理论声压(法向振速)和分离声压(法向振速)对比,说明有干扰源存在时,测量声压(法向振速)与理论声压(法向振速)存在较大的差异,通过提出的方法获得的声压(法向振速)与理论声压(法向振速)具有很好吻合,证明了该方法能实现较好的分离。 (2)将所提声场分离推广到具有多个声源时,通过仿真实验验证了该方法在多个声源时仍然具有较高的分离精度。 (3)对声场分离的影响因素(信噪比、等效源数目)仿真分析,得到信噪比对声场分离具有影响,随信噪比的增加,声场分离精度升高;声场分离对等效源点个数不敏感。1.3 单全息面声场分离

2 数值仿真
2.1 两个脉动球源仿真
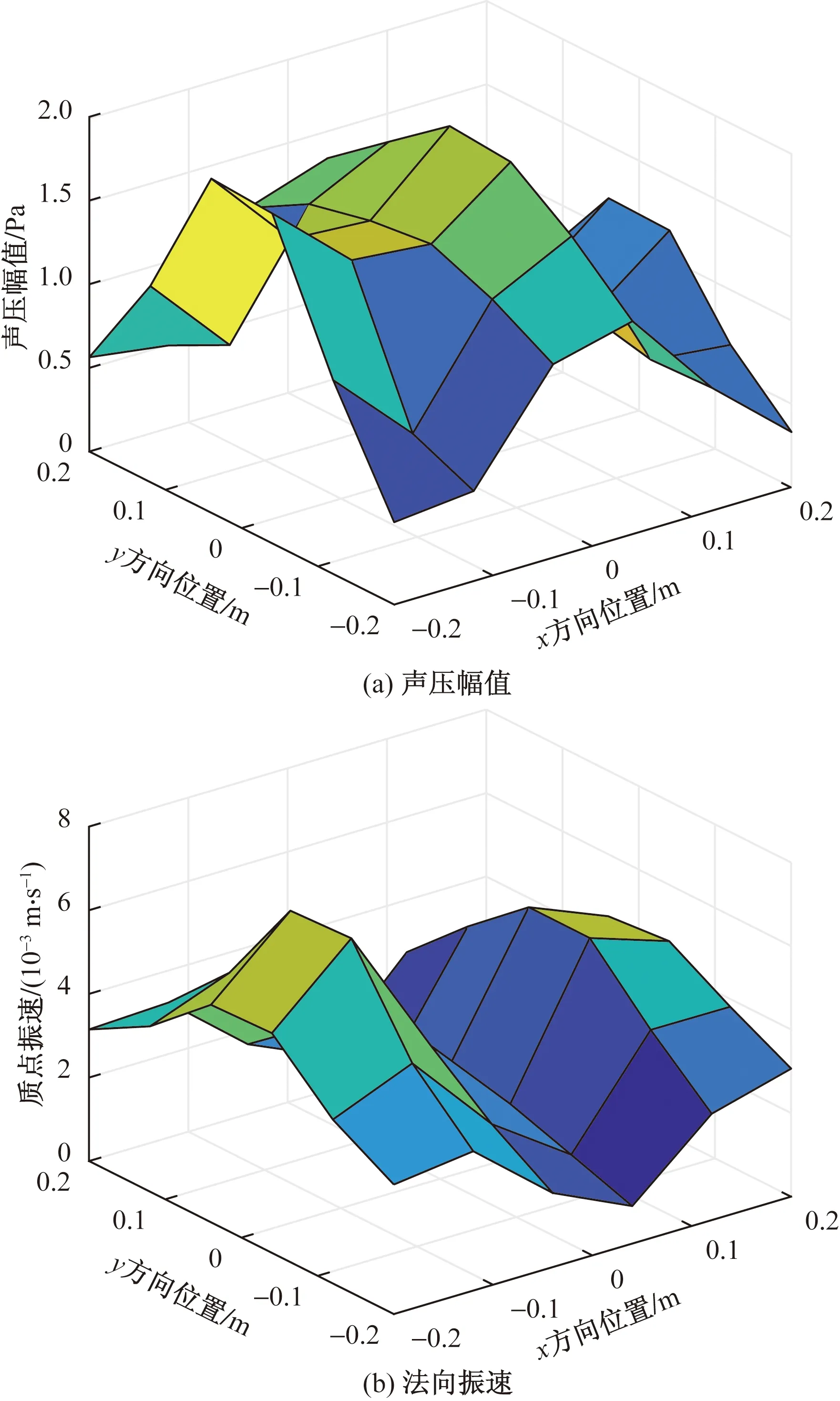
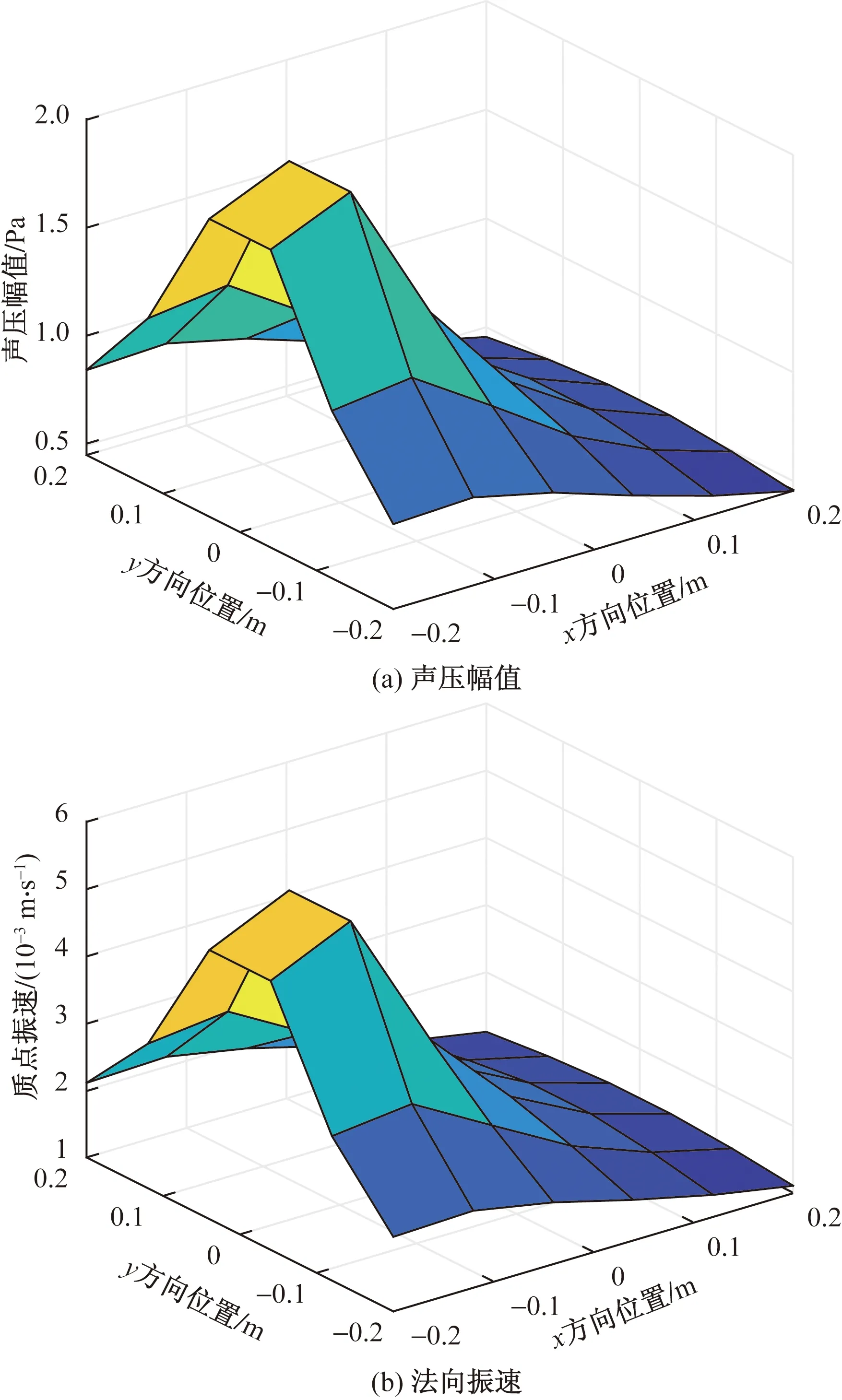
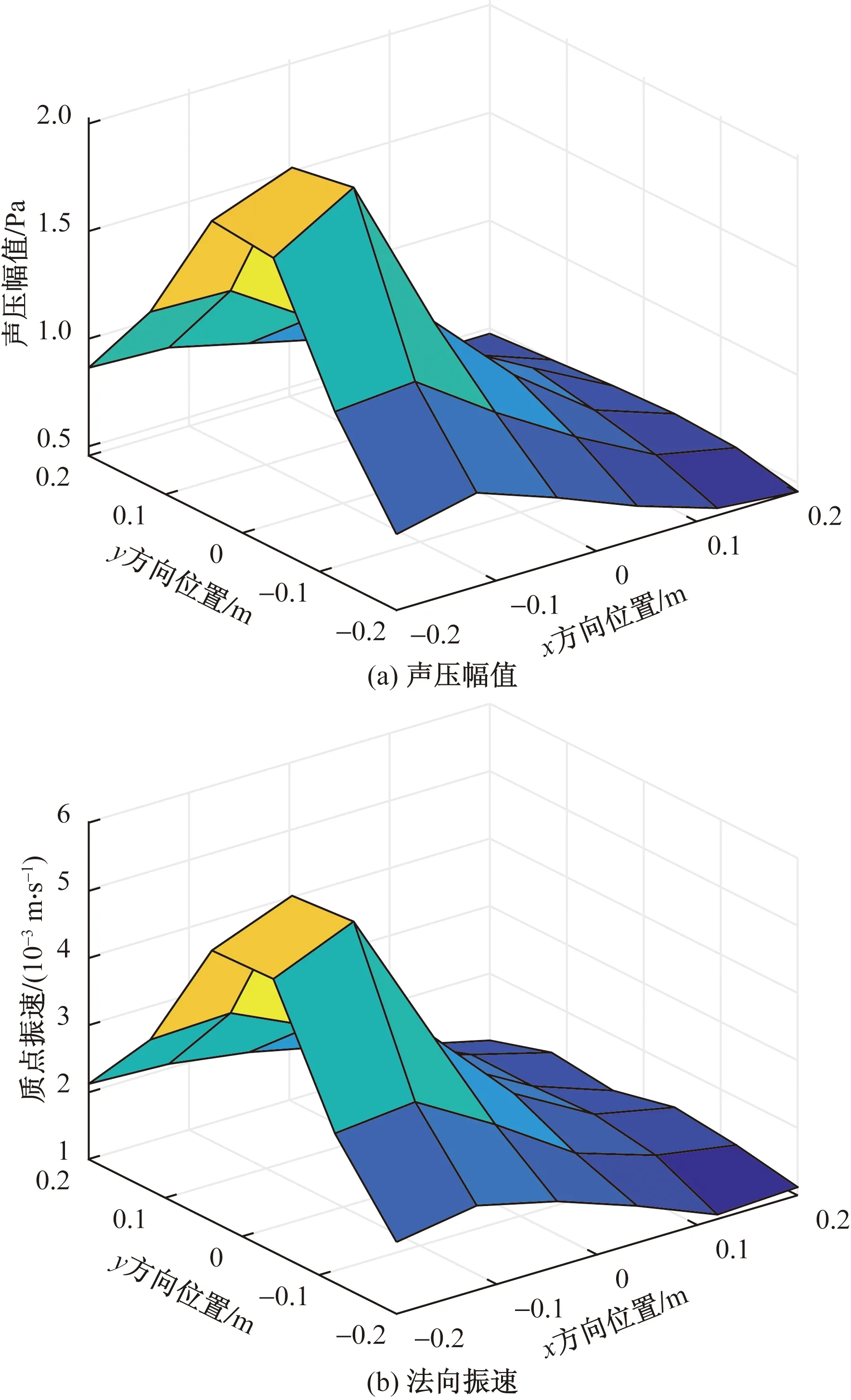

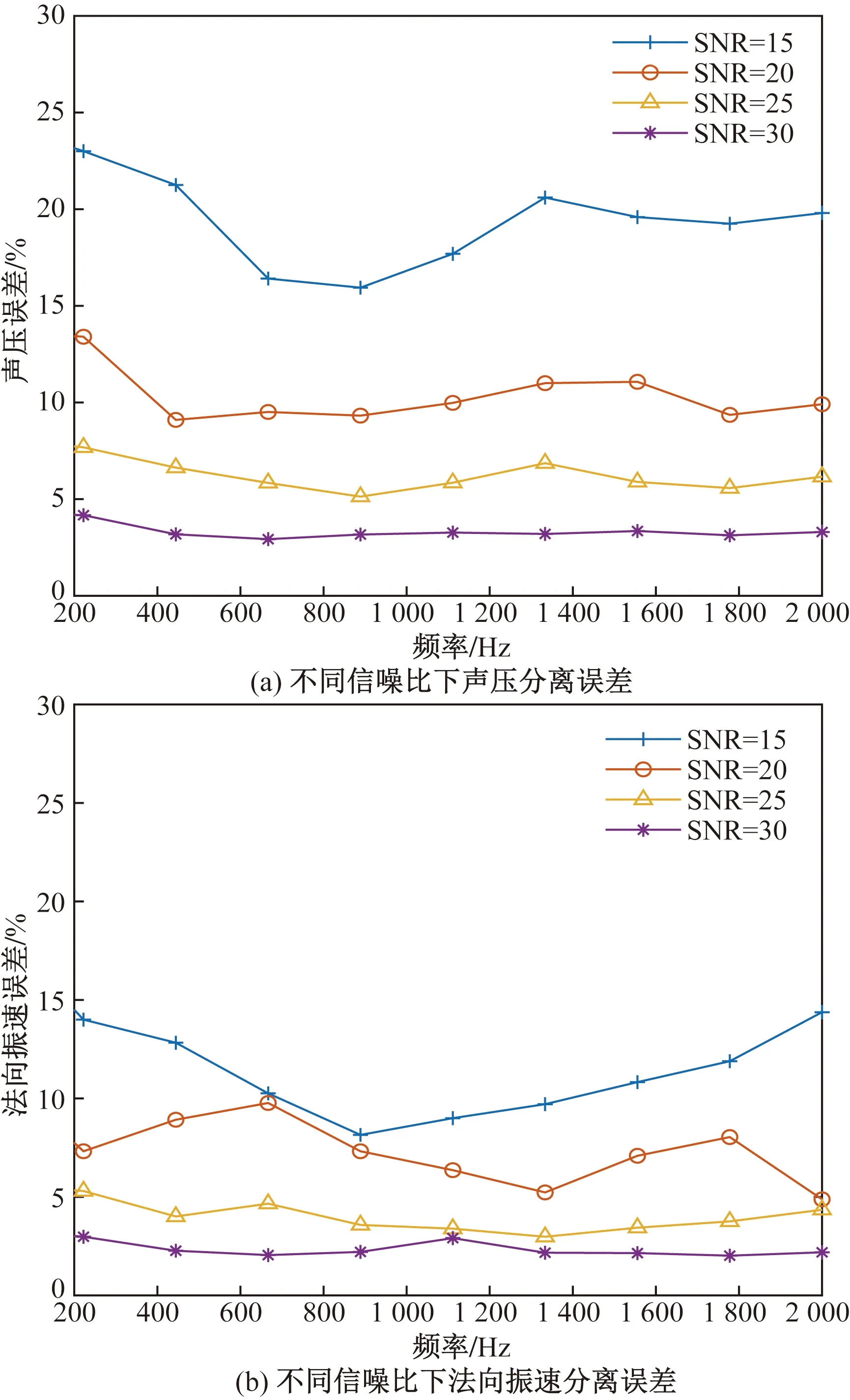
2.2 三个脉动球源仿真

3 结论
