纯电动汽车PMSM+AMT 换挡控制策略

杨镇瑜，韩胜明，陈桥松，屈凡林，尹育隆，阴晓峰*

（1.西华大学汽车工程研究所,四川 成都 610039；2.成都汽车产业研究院,四川 成都 610101；3.成都美云智享智能科技有限公司,四川 成都 610095）

电动汽车因其污染小、能量来源广泛等优点，已成为未来汽车的发展方向。目前纯电动汽车较多采用永磁同步电机（permanent magnet synchronous motor,PMSM）加单级减速器的结构，但这种结构会使电机在很大的转速和转矩变化范围内工作，导致整体运行效率受限，所以国内外对纯电动汽车用变速器的研究与应用越来越重视[1]。赵玉才[2]在MATLAB/Simulink 中建立了纯电动汽车机械自动变速器（automated manual transmission,AMT）执行机构模型，设计了PID 控制器，仿真结果表明能实现快速精确地换挡。赵伟桦[3]制作了动力传动系统的硬件，然后以CAN 通信为基础，监测处理车辆状态、驱动电机以及智能检测换挡间距等功能。Kim 等[4]提出了一种新的移位序列补偿速度控制算法，以降低AMT 的换挡冲击。岳汉奇[5]以基于multi-route 技术路线采用后置离合器滑摩助力换挡的I-AMT（inverse-automatic mechanical Transmission）为研究对象，提出了扰动抑制控制器，优化了滑摩功损失和车辆冲击度，与LQR（linear quadratic regulation）控制器相比，减小了换挡冲击度。悉尼科技大学 Tian 等[6]提出了一种最优控制器，在转矩相阶段的优化目标为车辆冲击度和滑摩功，在惯性相阶段的控制目标为减少滑摩功，结果表明此控制器能提高换挡品质。Walker 等[7]建立了驱动电机和变速器同步机构模型，采用转速和扭矩的闭环控制来优化换挡过程。Li 等[8]利用线性二次型控制算法，实现了对离合器的最优控制。Gao 等[9]以带有后置离合器的 AMT 为研究对象，制定了相应的控制策略，并采用PID 控制算法来控制惯性相阶段的离合器，以实现无动力中断换挡。

本文针对PMSM+AMT 多挡电驱变速系统，提出了卸载、同步、转矩恢复等阶段的优化控制策略，进而提升换挡品质。首先建立了PMSM+AMT电驱变速系统的动力学模型，分析换挡时不同阶段的工作情况，并以换挡冲击度以及换挡时间为评价指标，提出了各个阶段相应的控制策略，最后在MATLAB/Simulink 中建立仿真模型，验证了控制策略的有效性。

1 PMSM+AMT 系统动力学模型

本文研究的电驱变速系统中，PMSM 输出轴与AMT 输入轴直连，驱动电机输出转矩直接传递到AMT 输入轴，再由AMT 输出轴传递到主减速器、车轮，驱动车辆行驶。通过分析动力传动系统的数学模型，得到传动系统受力简图，如图1 所示。

图1 传动系统受力简图Fig.1 Schematic diagram of transmission system stress

图1 中从左至右依次代表PMSM、AMT、主减速器、整车。驱动电机输出转矩Tm至变速箱输入轴，变速箱输出转矩Tto至主减速器输入端，经主减速器后输出转矩To给整车，整车克服行驶阻力Tw进行行驶。图中：ig、io分别表示传动系统中变速箱和主减速器的传动比；ωm、ωto、ωo、ωw分别表示PMSM、变速器输出轴、主减速器输出轴、车轮的角速度，rad/s 。

1.1 PMSM 驱动电机模型

在dq坐标系下，PMSM 的电压方程式[10]可表示为

式中：ud、uq、id、iq为定子电压和电流在d、q轴下的分量，V、A；ωe为当前PMSM 的转子磁链旋转角速度，rad/s；Ld、Lq分别为dq坐标下PMSM 的电感分量，H；Rs为定子电阻，Ω；ψf为合成的转子磁链，Wb。

电机磁链方程[10]为

式中：ψd、ψq为dq坐标下的磁链分量，Wb。

电机转矩方程[11]为

式中：Te为电机电磁转矩，N·m；p为极对数。

电机机械运动方程[11]为

式中：TL为驱动电机的负载转矩，N·m；Jm为PMSM 的转动惯量，kg·m2；ωm为PMSM 的转子转动角速度，rad/s；B为驱动电机的阻尼系数。

1.2 无离合器AMT 系统模型

1.2.1 在挡模型

当变速器在挡行驶时，PMSM 的输出转矩经过变速箱到达主减速器，再通过传动轴传递给车轮，以驱动汽车行驶。系统动力学方程[12]如下:

式中：Jti、Jto、Jo、Jw为AMT 输入轴、输出轴、主减速器以及车轮的转动惯量，kg·m2；Tmf、Tw分别为驱动电机摩擦转矩、整车行驶阻力转矩，N·m；k、b分别为驱动轴弹性、阻尼系数；φo、φw分别为主减速器输出轴、车轮的转动角度，rad；ωw为车轮的角速度，rad/s；rw为车轮的半径，m；m为汽车总质量，kg。

1.2.2 空挡模型

处于空挡状态时没有动力输出，其动力学方程为

式中：ωto为AMT 输出轴角速度，rad/s；To为主减速器输出轴转矩，N·m。

1.2.3 摘挂挡模型

摘挂挡时，控制的主要对象是啮合套。对拨叉施加沿齿轮轴的轴向力，产生摩擦力矩，从而使同步器主、从动部分的转速差逐渐减小至0[13]。在理想条件下，由转矩、转动惯量与角加速度的关系可得同步器主动端、从动端的动力学方程分别为

式中：Ts为同步器主动端的输入转矩，N·m；Jm为PMSM 的转动惯量，kg·m2；ωm1为同步器从动端的角速度，rad/s；Jc为同步器的转动惯量，kg·m2；sign为符号函数。

2 换挡控制策略

2.1 控制系统结构

在换挡过程中，首先由整车控制器 (vehicle control unit，VCU)根据车辆状态判断是否需要进行换挡，若需要换挡则发出指令给变速器-电机集成控制器(transmission-motor control unit，T-MCU)启动换挡过程。集成控制器根据换挡过程各阶段相应的控制策略，得到驱动电机及变速器的需求，并根据传动系统反馈的信息，判断换挡过程各个阶段的执行情况，使整车能够顺利完成换挡并传递换挡结束信息给VCU。PMSM+AMT 换挡控制系统结构如图2 所示。

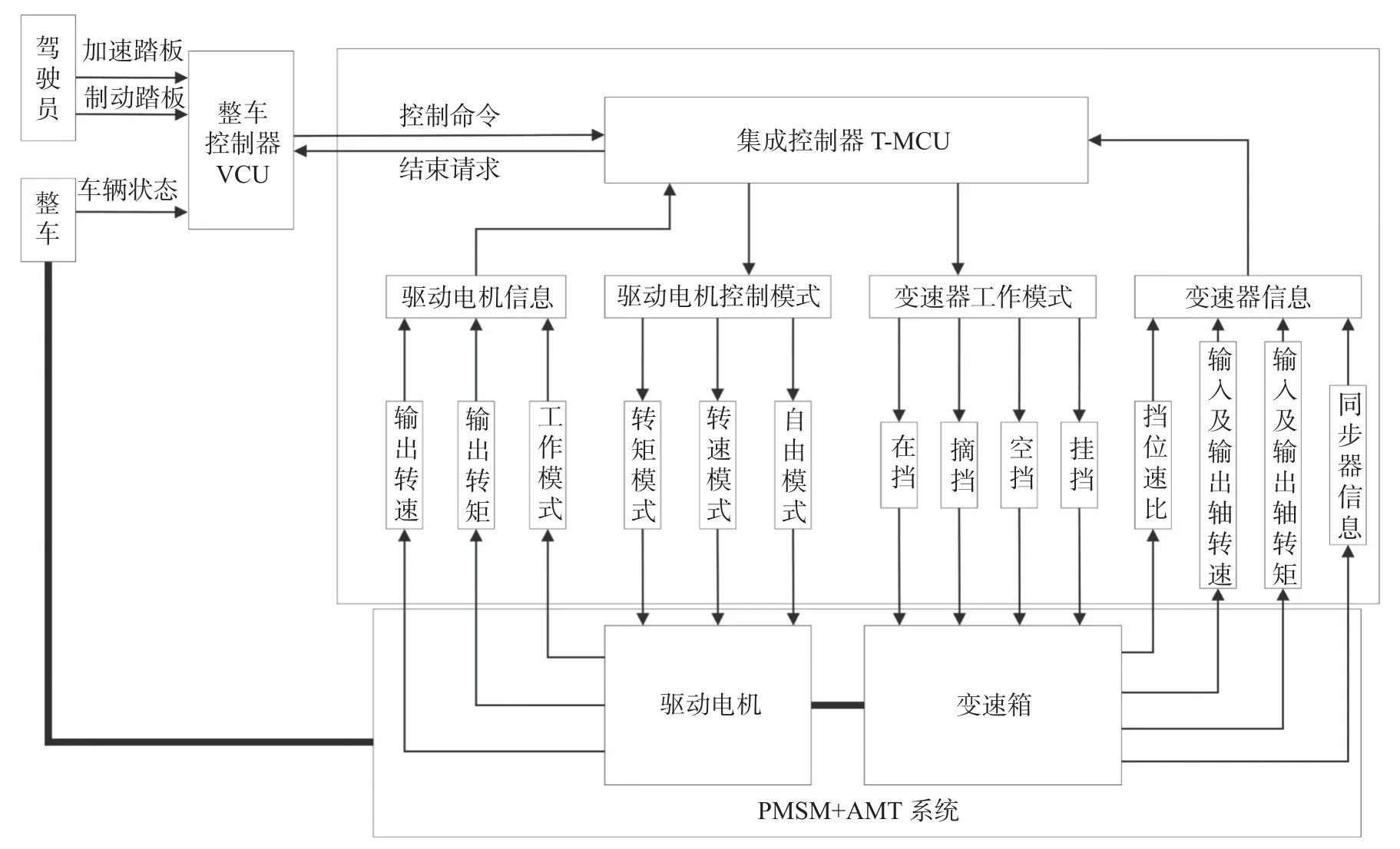
图2 PMSM+AMT 换挡控制系统结构Fig.2 PMSM+AMT shift control system structure

2.2 换挡控制策略

PMSM+AMT 系统换挡过程可分为5 个阶段。卸载阶段电机应处于转矩模式，摘挡阶段电机由转矩模式转换为自由模式，同步阶段电机应处于转速模式，挂挡阶段电机处于自由模式，转矩恢复阶段电机恢复到转矩模式[14]。在这5 个阶段中AMT 处于卸载、摘挡、同步、挂挡、转矩恢复5 种状态之一。

1）卸载。

T-MCU 控制驱动电机降低输出转矩，为了避免驱动电机输出转矩脉动，需要控制驱动电机的输出转矩以一定的速率降低。结合式（4）和式（5）可推导出驱动电机在卸载阶段的转矩变化率应满足

式中：k1为卸载阶段的转矩变化率；Tm1为卸载阶段驱动电机的输出转矩，N·m；Tw1为准备摘挡过程行驶阻力矩，N·m；j为冲击度，m/s3。

2）摘挡。

当集成控制器接收到驱动电机输出转矩降低至目标转矩时的信息后卸载阶段完成，集成控制器发出摘挡控制指令给换挡执行机构，摘挡过程开始，同步器开始分离，当到达相应的位置后反馈信息给集成控制器，集成控制器判定摘挡阶段结束。

摘挡时由于驱动电机和变速器会有转速差产生，此时整车的驱动力矩为同步器的滑摩转矩，故在滑摩阶段的同步器滑摩转矩[12]应满足

式中：k2为摘挡过程同步器目标滑摩转矩变化斜率；Ms为同步器滑摩转矩，N·m；Tw2为行驶阻力矩，N·m，可忽略不计。

3）同步。

驱动电机进入转速模式，并开始进行主动调速。根据测得的同步器从动端的转动速度来计算PMSM 的目标转速[15]。

式中：igtar为目标挡位传动比；为PMSM 的目标转速，rad/s；ωm1为同步器从动端的角速度，rad/s；Δωm1为预设转速偏差，rad/s。

当转速差缩小到设定值，AMT 接收到集成控制器发送的同步指令，开始施加同步力矩，使同步器通过其主从部分的滑磨作用，进一步减小两端的转速差，直至到达目标值。

4）挂挡。

驱动电机进入自由模式。驱动电机在此阶段的转速初始值与上一阶段的结束值相同，转矩初始值与上一阶段的结束值一致。此阶段由换挡电机带动换挡执行机构进行相应的挂挡动作。对于挂挡过程的控制，为了缩短换挡时间，因此只考虑换挡执行机构能够快速挂挡。

5）转矩恢复。

驱动电机的目标转矩确定方法与准备摘挡阶段类似，也根据冲击度标准来制定转矩恢复变化率。转矩初始值为挂挡结束时的驱动电机转矩，变化率应尽可能大，以减小换挡时间。结合式（4）和式（5）可推导转矩恢复的变化率应满足

式中：k3为转矩恢复过程目标转矩曲线斜率；Tm3为电机输出转矩，N·m；Tw3为挂挡过程行驶阻力矩，N·m。

2.3 基于查表的MTPA 驱动电机控制算法

采用基于空间矢量脉宽调制算法以及最大转矩电流比控制（space vector pulse width modulationmaximum torque per ampere,SVPWM-MTPA）方法控制驱动电机[16]。通过确定旋转坐标系下的d轴电流来充分利用磁阻转矩，使驱动电机在输出相同转矩的情况下其定子电流最小。将定子电流分解为d、q轴电流，可得到d、q轴的电流满足：

式中：is为PMSM 的定子电流矢量，A；β为PMSM的定子电流矢量和d、q轴坐标的电流矢量夹角。

通过拉格朗日极值定理可以构造出的辅助函数为

式中：F为拉格朗日函数；λ为拉格朗日的乘子。对函数F求偏导[16]，得到

电流矢量夹角满足

得到各转速、转矩值对应的最佳id、iq值。在仿真模型中采用基于查表法的MTPA 控制策略，并使用前馈解耦控制算法以提高系统的动态响应特性，通过SVPWM 控制逆变器以达到控制驱动电机的目的。MTPA-SVPWM 控制策略如图3 所示。

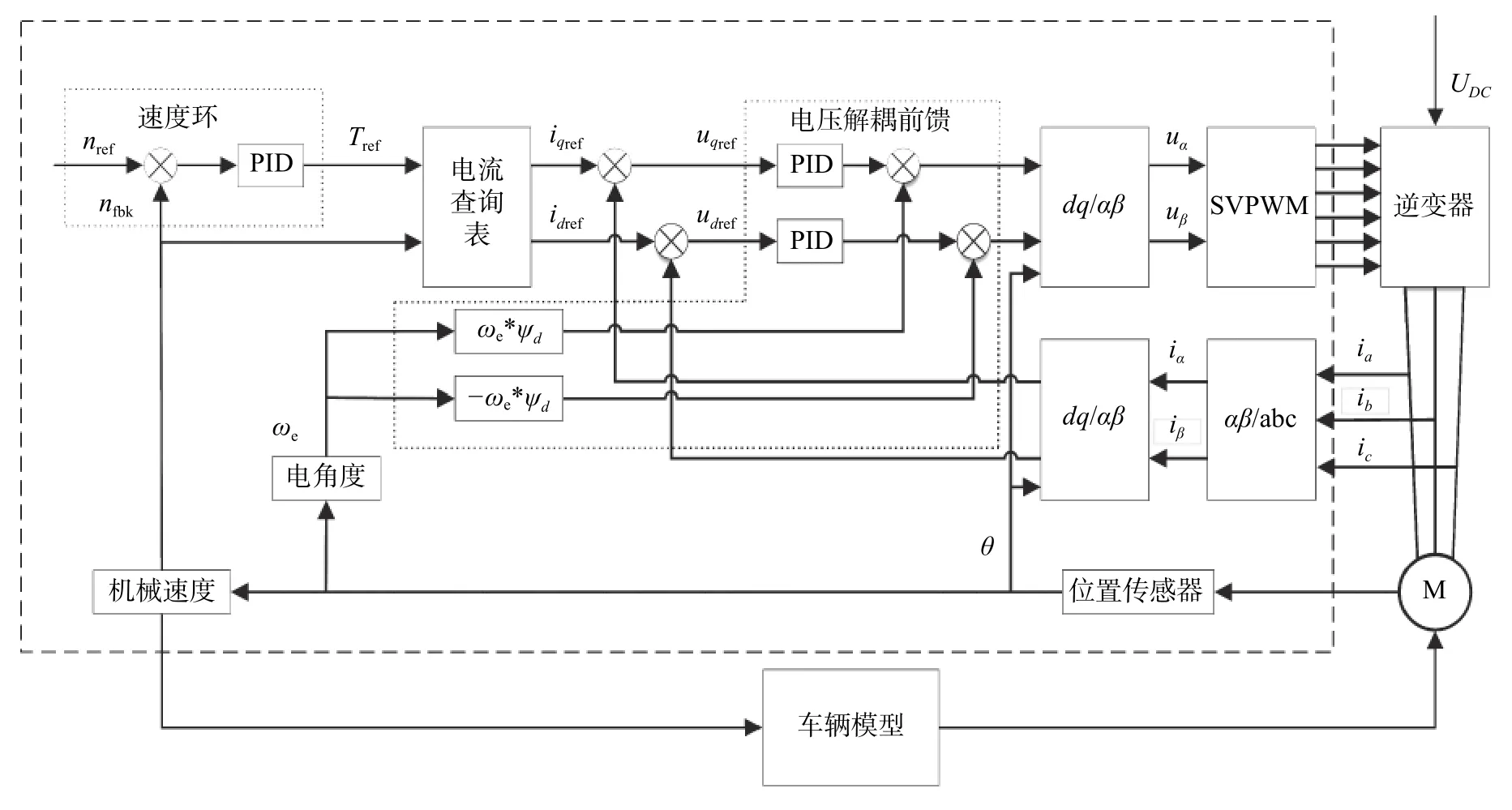
图3 MTPA-SVPWM 系统原理框图Fig.3 MTPA-SVPWM system schematic diagram

采用MTPA 控制时，以速度环为例，通过传感器获得反馈速度，将目标转矩作为PID 控制器的输出。通过查询PMSM 的目标转矩与实际转速，得到d、q轴的目标电流，并通过电流表查询控制目标d、q轴电压udref、uqref，经过电压前馈解耦控制后输出电压矢量uα、uβ，最后经SVPWM 调制得到逆变器控制信号。

对于凸极型的PMSM，其转矩的变化率与PMSM的定子磁链、转矩角以及转矩角的变化率有关，通过确保转矩变化率为正来保证转矩是随着转矩角的增大而增大。当凸极系数大于1 时，应满足

式中，ψs为定子磁链矢量，Wb。

磁链的值可以通过测量定子的电压和电流等物理量来建立磁链模型，然后间接计算估计获得。基于电压-电流模型可将其表示为[17]

式中：us为定子电压，V；is为定子电流，A。

在实际的控制方式中，会采用低通滤波器来代替纯积分器，但这种改进会带来定子磁链的幅值与相位误差[18]，而空间矢量脉宽调制理论可以较好地解决这个问题。SVPWM 的理论是平均值等效原理[19]，需要将电压进行分解，SVPWM 电压矢量分解如图4 所示。

图4 SVPWM 电压矢量分解图Fig.4 SVPWM voltage vector decomposition diagram

SVPMW 控制算法下的空间电压矢量可表示为

式中：ua、ub、uc为三相的电压矢量；utotal为合成的空间电压矢量；θ为合成的空间电压矢量的角度，rad，可表示为θ=2πft，其中f为电源频率，t为时间。

通过将360 度的电压空间分为60 度一个扇区，共6 个扇区，利用这6 个基本有效矢量和两个零量可以合成360 度内的任何矢量。为了得到逆变器的目标开关时间，可以将合成的空间电压矢量分解到轴上，并可进一步控制磁链的合成[12]。

3 仿真验证

3.1 仿真模型

为了验证所提策略的有效性，使用MATLAB/Simulink 软件建立了整车的仿真模型。该模型主要由PMSM 模块、AMT 模块和整车纵向动力学模块组成。

PMSM 模块如图5 所示。以转速模式为例，PMSM 接收到目标转速值，与实际转速作差，差值作为PID 控制器的输入，输出当前目标转速下的期望转矩，进行限制后查询MTPA 控制策略表，得到最佳的d、q轴电流值，并结合前馈解耦控制计算出d、q两相电压，通过SVPWM 求得占空比，输入到三相桥臂，从而控制转速。

图5 PMSM 模块Fig.5 PMSM module

AMT 模块如图6 所示，主要模拟换挡过程中变速器的动力学行为。其输入为当前挡位、PMSM的输出转矩、转速和变速器工作模式，输出为变速器输入轴的转矩及转速、变速器输出轴的转矩及转速以及同步器状态信息。

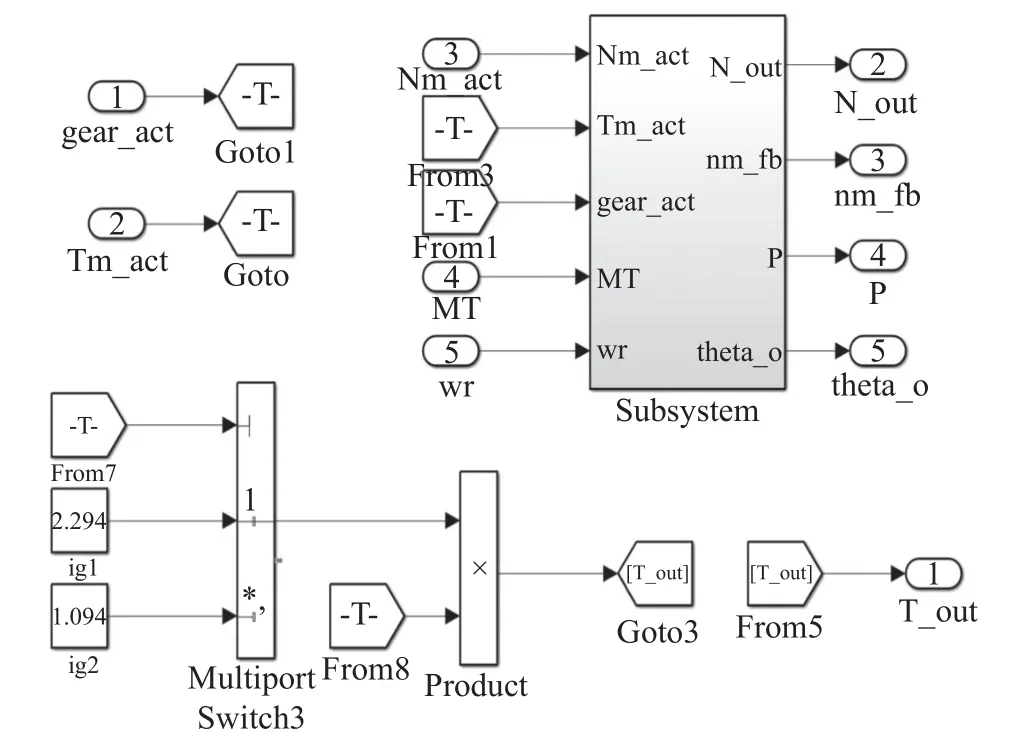
图6 ATM 系统模型Fig.6 ATM system model

整车纵向动力学模块如图7 所示，主要模拟换挡过程中整车的纵向动力学行为。其输入为主减速器的输出转矩、当前挡位、整车质量、坡度和制动力，输出为车速。

图7 整车模型Fig.7 Vehicle model

仿真参数：整车质量m为1 450 kg；车轮半径rw为0.316 m；空气阻力系数CD为0.32；滚动阻力系数f为0.015；迎风面积A为2.45 m2；驱动电机额定/峰值功率为45/90 kW，额定/峰值转速为2 200/6 000 r/min，额定/峰值转矩为195/300 N·m；动力电池简化为恒定电压放电，其容量为20.7 kWh；传动系统的主减速比为i0=6.8，一挡传动比为i1=1.6，二挡传动比为i2=0.95。

3.2 仿真分析

以10%、30%、60%加速踏板开度下1 挡升2 挡为例，纯电动汽车换挡过程的PMSM+AMT 系统输出转矩、输出转速、冲击度的仿真结果如下。

1）10%加速踏板开度。

10%加速踏板开度的仿真结果如图8 和9 所示。51.032 s 之前为纯电动汽车的加速过程，51.032～51.045 s 为卸载阶段，51.145～51.307 s 为同步阶段，51.407～51.415 s 为转矩恢复阶段，之后整车继续加速。整个换挡过程耗时0.383 s。

图8 10%加速踏板开度转矩、转速、车速Fig.8 10% accelerator pedal opening torque,rotational speed,speed

图9 10%加速踏板开度冲击度Fig.9 10% accelerator pedal opening impact degree

对于升挡过程电机输出转矩曲线，可以看出卸载阶段转矩从12.1 N·m 开始线性下降，摘挡过程迅速调节输出转矩至0，同步过程中断动力传递，挂挡过程驱动电机输出转矩逐渐回升，转矩恢复过程转矩进一步增大，最终达到19.53 N·m 的转矩后开始下降。

驱动电机在卸载阶段处于转矩模式，驱动电机的输出转矩开始逐渐降低，当驱动电机的输出转矩开始小于负载后，驱动电机趋于倒拖状态。同步阶段没有动力输出，整车进行惯性行驶，在51.407 s同步阶段结束后，进入动力恢复阶段，驱动电机的转速输出与自动变速器的转速输入逐渐相同，整个过程的转速未出现明显超调。

从51.043 s 开始，整车驱动力开始小于行驶阻力，车速开始下降；经过摘挡、同步、挂挡等阶段后，在51.42 s 时，驱动力开始大于行驶阻力，车速开始上升。

根据冲击度仿真可以看出，在10%加速踏板开度下的换挡过程中，PMSM+AMT 系统在卸载阶段的最大冲击度为-9.89 m/s3；加载阶段的最大冲击度为9.8 m/s3。

2）30%加速踏板开度。

30%加速踏板开度的仿真结果如图10 和11 所示。18.401 s 之前为纯电动汽车的加速过程，18.401～18.445 s 为卸载阶段，18.545～18.752 s 为同步阶段，18.852～18.881 s 为转矩恢复阶段，之后整车继续加速。整个过程耗时0.48 s。

图10 30%加速踏板开度转矩、转速、车速Fig.10 30% acceleration pedal opening torque,rotational speed,speed

图11 30%加速踏板开度冲击度Fig.11 30% acceleration pedal opening impact degree

从升挡过程电机输出转矩曲线可以看出，卸载阶段转矩从29.66 N·m 开始线性下降，摘挡过程迅速调节输出转矩至0，同步过程中断动力传递，挂挡过程驱动电机输出转矩逐渐回升，转矩恢复过程转矩进一步增大，最终达到50.11 N·m 的转矩后开始下降。

在18.545 s 开始同步，整车动力中断，整车进行惯性行驶，18.752 s 同步阶段结束后，进入动力恢复阶段，驱动电机的转速输出与自动变速器的转速输入逐渐相同，整个过程的转速未出现明显超调。

从18.441 s 开始，整车驱动力开始小于行驶阻力，车速开始下降；经过摘挡、同步、挂挡等阶段后，在18.867 s 时，驱动力开始大于行驶阻力，车速开始上升。

根据冲击度仿真可以看出，在30%加速踏板开度下的换挡过程中，PMSM+AMT 系统在卸载阶段的最大冲击度为-9.92 m/s3，加载阶段的最大冲击度为9.83 m/s3。

3）60%加速踏板开度。

60%加速踏板开度的仿真结果如图12 和13所示。9.36 s 之前为纯电动汽车的加速过程，9.36～9.45 s 为卸载阶段，9.55～9.77 s 为同步阶段，9.87～9.94 s 为转矩恢复阶段，之后整车继续加速。整个过程耗时0.58 s。

图12 60%加速踏板开度转矩、转速、车速Fig.12 60% accelerator pedal opening torque,rotational speed,speed

图13 60%加速踏板开度冲击度Fig.13 60% accelerator pedal opening impact degree

从升挡过程电机输出转矩曲线可以看出，卸载阶段转矩从56 N·m 开始线性下降，摘挡过程迅速调节输出转矩至0，同步过程中断动力传递，挂挡过程驱动电机输出转矩逐渐回升，转矩恢复过程转矩进一步增大，最终达到94.58 N·m 的转矩后开始下降。

在9.55 s 开始同步，整车动力中断，整车处于惯性行驶阶段，在9.77 s 同步过程结束后，进入动力恢复阶段，驱动电机的转速输出与自动变速器的转速输入逐渐相同，整个过程转速未出现明显超调。

从9.44 s 开始，整车驱动力开始小于行驶阻力，车速开始下降。经过摘挡、同步、挂挡等阶段后，在9.89 s 时，驱动力开始大于行驶阻力，车速开始上升。

根据冲击度仿真可以看出，在60%加速踏板开度下的换挡过程中，PMSM+AMT 系统在卸载阶段的最大冲击度为-9.96 m/s3，加载阶段的最大冲击度为9.86 m/s3。

结果表明，本文所提的换挡控制策略在整个换挡过程中产生的最大冲击度均未超过德国冲击度标准10 m/s3，且换挡时间皆少于0.6 s，满足换挡品质要求。

4 结论

基于空间矢量脉宽调制的最大转矩电流比控制方法能有效降低电机输出转速及转矩脉动，提高纯电动汽车的动态响应，以满足不同道路工况下的需求。经过在不同加速踏板开度下的验证，本文提出的PMSM+AMT 系统换挡控制策略能使纯电动汽车的换挡时间较短，驱动电机输出转矩变化平稳，升挡过程电机转速无明显超调，系统冲击度满足标准要求，提高了驾乘舒适性。但由于本文采用的是基于冲击度上限的控制策略，通过调整上限值，冲击度还有优化的空间。