基于微波时间反演算法的复合材料内部损伤检测

安 康,李长侑,丁 君

(西北工业大学 电子信息学院,西安 710129)

纤维增强复合材料是一种由玻璃纤维、碳纤维 和芳纶纤维等纤维材料和树脂、陶瓷等基体材料构成的新型高性能材料,具有质量轻、比强度高、耐疲劳、耐腐蚀等优点,是一种发展潜力巨大的新型军民两用材料,在航空航天、汽车工业、建筑材料、电子和医疗等领域都具有广阔的应用前景。然而,复合材料在生产或使用过程中,难以避免地会产生裂纹、空洞、分层、脱黏等损伤,这些损伤的存在会严重影响纤维增强复合材料的硬度、延展性等机械特性,严重威胁航空航天、汽车、建筑等领域中复合材料部件的使用安全。因此,研究高效、准确的复合材料无损检测技术具有重要意义。

目前,常用的无损检测技术包括微波检测技术[1]、超声检测技术[2-3]、红外热成像检测技术[4-5]、X 射线检测技术[6-7]、涡流检测技术[8-9]等。其中,微波检测技术具有非接触、实时、高效、高对比度的优势,是进行快速复合材料无损检测的重要手段。美国在20世纪60年代就采用微波技术对大型导弹固体发动机玻璃钢壳体中的缺陷和内部质量进行检测。我国的陆荣林等[10-11]采用微波反射技术对不同复合材料中的空洞型缺陷进行了检测,结果证明了微波检测技术对复合材料中缺陷检测的有效性。2019年,MEIER等[12]使用了毫米波雷达对复合材料散射场进行测量,利用信号相位的高灵敏度对复合材料内部的断层损伤进行了成像。2020年,AMINEH 等[13]提出了一种基于近场微波三维成像和波束空间变换的方法实现了对非金属管道中缺陷的检测,并进行了相关试验验证。

在复合材料的无损检测中,微波检测技术可以弥补其他常规检测方法的不足(如超声波在复合材料中衰减大、难以检测内部较深缺陷;X射线检测技术对平面型缺陷的检测灵敏度低等缺点),对复合材料结构中的孔隙、疏松、基体开裂、分层和脱黏等缺陷具有较高的灵敏度。然而,微波检测技术分辨率通常较低,在损伤小于所适用的微波波长时,不容易被检测到。

时间反演算法最早由FINK 在1992年提出,在超声领域得到了广泛应用。微波时间反演算法是将信号接收单元记录的辐射信号或者散射信号在时域中进行一种反转操作,然后将反转后的信号从相应的接收单元处辐射回原辐射区域或散射区域,则反转后的信号会自适应地在辐射源或者散射体处产生空时聚焦。2004年,LEROSEY等[14]完成了第一个微波电磁场中的时间反转试验,在一个具有高品质因素的腔体中,采用单发射天线-单接收天线的结构利用时间反演算法实现了在发射天线位置处的空时聚焦。2007年,CARMINATI等[15]在时间反转腔中从矢量波的角度推导了时间反演算法的空时聚焦特性。2010年,DE等[16]给出了单色时间反转镜的理论推导,同样推导得到了时间反演算法的空时聚焦特性。这种对环境自适应的空时聚焦特性使得时间反演算法在探测领域具有了巨大的应用潜力。2017年,WANG 等[17]通过设置近场辅助源,提出了一种实现超分辨率成像的时间反演算法。2018年,MUKHERJEE等[18]研究了微波时间反演算法用于复合材料无损检测的可行性,并通过试验证明了该技术具有检测复合材料和金属黏接层中单个和多个脱黏损伤的能力。2021年,MUKHERJEE等[19]提出了一种结合多个辐射源的时间分辨信息进行复合材料损伤检测的微波时间反演算法,其可以对复合材料中的平面型损伤进行检测,并通过仿真进行了验证。

文章基于二维时域有限差分算法对复合材料模型进行数值仿真,结合微波时间反演算法和积分能量法对复合材料内部较小损伤进行检测,研究了不同传感器排列方式和传感器数量对检测结果的影响,实现了复合材料内部较小损伤的检测,并讨论了提升检测质量的关键因素。

1 微波时间反演算法

微波时间反演算法是指在使用微波脉冲信号辐射待测材料后,将信号接收单元记录的辐射信号或者散射信号在时间上进行反转,然后将反转后的信号从相应的接收单元处辐射回原辐射区域或散射区域,则反转后的信号将在同一时刻在原始信号源或目标所在的位置产生自适应的相干叠加,即为自适应的空时同步聚焦特性。

1.1 时间反转不变性

时间反演算法的基本理论是基于波动方程在无耗和时不变介质中的时间反转不变性。由于电磁场波动方程在时间上具有对称性,所以波动方程包含两个解:一个解是描述发散波的解ϕ(r,t),另一个是描述收敛波的解ϕ(r,-t)。发散波是指从脉冲源辐射出的电磁波,收敛波则是指从空间中收敛至脉冲源位置处的电磁波。在时间反转的操作下,这两个解依旧满足波动方程。因此,收敛波将会沿着发散波的传播路径在脉冲源的位置处实现自适应聚焦。给出标量波动方程如下[20]

式中:ε和μ为介电常数和磁导率。

1.2 无损检测中的时间反演算法

在微波时间反演算法中,时间反转后的信号会自适应地在该信号所经过的目标或信号源处聚焦,然而在传感器上测量得到的信号通常是脉冲信号经过多个散射体的多次散射后得到的散射信号,直接对该散射信号进行时间反转和回传无法使其在目标位置聚焦。因此,为了获得与目标相关的散射信号,需要采用背景相消法[21],即对健康模型的散射信号进行测量,并将其作为参考信号。在对损伤模型进行测量时,将测量得到的散射信号减去参考信号,以得到与待测目标相关的散射信号,并将该信号称为扰动信号。通过将扰动信号在时间上进行反转,并回传到原健康模型中,时间反转后的扰动信号会自适应地在待测目标处实现聚焦。这一理论为时间反演算法在无损检测中的应用奠定了理论基础。

1.3 基于时域有限差分法的时间反演算法

文章基于二维时域有限差分数值算法对复合材料的数值模型进行仿真。时域有限差分算法的优势在于可以更加直观地观察在时间反演过程中电磁场的变化规律,有利于更好地对时间反演算法的聚焦过程进行分析。

在微波时间反演算法中,脉冲宽度决定了算法的纵向分辨率,因此,通常采用短微波脉冲信号作为信号源。文章采用高斯调制脉冲作为微波脉冲源,表达式如下

式中:中心频率fc为20 GHz(对应波长λ为15 mm);影响脉冲带宽的参数τ为20 ps;微波脉冲信号的时间延迟t0为0.1 ns。

取Δx=Δy=λ/30=0.5 mm,Δt=0.8 ps,基于上述参数,产生的微波脉冲信号的时域波形和频域波形如图1所示。

1.4 目标定位算法

在采用微波时间反演算法进行无损检测的过程中,对散射信号的全面准确测量和有效的目标定位算法是影响检测结果的两个重要因素。散射信号的测量与传感器数量和排列方式相关。文章将积分能量法作为目标定位算法,积分能量法可以在时间反演算法中进行损伤定位,已有应用于复合材料和金属黏接层的损伤检测报道[18]。时间反转信号与材料内部属性分布相关,且在损伤位置处会产生尖锐的峰值。因此,对时间反转电场在时间上进行能量积分,积分能量图像中最大能量位置即代表了时间反转信号聚焦的目标位置。积分能量的公式如下[20]

式中:W(x,y)为每个位置处的积分能量;E z(x,y,t)为时间反演过程中每个位置处的电场;η(x,y)为每个位置处的本质阻抗;T为总时间。

2 数值仿真

2.1 传感器排列方式的影响

两个具有不同传感器排列方式的复合材料模型结构示意如图2 所示。计算区域的大小为100 mm×100 mm,在边界上使用完全匹配层(PML)边界条件来模拟自由空间。复合材料模型由玻璃纤维增强聚合物(GFRP,相对介电常数为4.6,长×宽为100 mm×30 mm,见图2中蓝色区域)、金属背板(图2中灰色区域)和材料内部的小型空气损伤(GFRP中的白色区域,长×宽为5 mm×2 mm,相对介电常数为1.0)组成。空气损伤设置在材料的横向中心位置,与GFRP下表面的距离dd为10 mm。将微波脉冲源建模为点源(传感器阵列中心的红色“×”),以激发所采用的高斯调制微波脉冲信号,微波脉冲源与GFRP下表面的距离ds为45 mm。在模型1中,59个传感器呈直线形均匀排列,与计算区域下边界的纵向距离为10 mm,每个传感器之间的距离为1.5 mm。在模型2中,59个传感器均匀分布在以点(50 mm,55 mm)为中心,45 mm 为半径的半圆上,每两个传感器之间的角度步进为3°。采用这种半圆形传感器排列方式的原因在于其可以接收来自复合材料模型的侧向散射信号,通过与直线形传感器排列方式的重构结果进行对比,分析传感器排列方式对重构结果质量的影响。

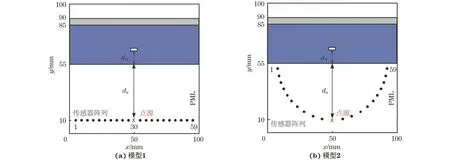
图2 两个具有不同传感器排列方式的复合材料模型结构示意

扰动信号是通过从损伤模型测量得到的散射信号中减去从健康模型测量得到的散射信号获得的。算法中,将扰动信号在时间上进行反转并传播至健康模型中。在两个模型中,所有传感器位置上计算得到的扰动信号如图3所示。比较两种模型的扰动信号,可以看出中间位置的传感器计算得到的扰动信号大小基本相同。然而,模型2中边缘位置上的传感器计算得到的信号中,第一个峰值明显小于模型1中同样位置的传感器所得到的信号峰值。这是由于模型1中的边缘位置上的传感器主要接收纵向散射波,而模型2中的边缘位置上的传感器接收的是侧向散射波。根据电磁波的传播方向,在仿真过程中产生的纵向散射波必然大于侧向散射波。对比两种传感器排列方式计算得到的扰动信号,其主要区别在于半圆形排列方式的传感器可以接收到来自材料的侧向散射波。

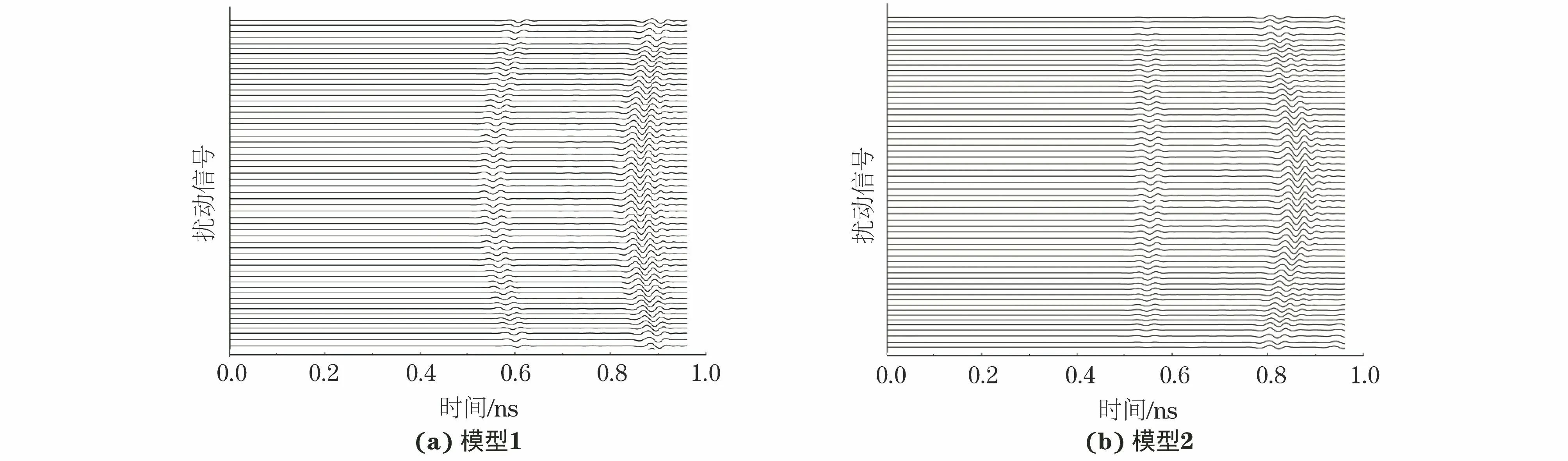
图3 两个模型中所有传感器计算得到的扰动信号

基于积分能量法,得到两种传感器排列方式下计算区域的归一化能量图像如图4所示。图4中虚线表示复合材料(黄色虚线)和金属背板(灰色虚线)的真实位置,白色实线框表示损伤的真实位置。在模型1的能量图像中,最大能量值出现在金属背板表面,并且大于真实损伤位置的能量,无法有效判断损伤位置。在模型2的能量图像中,最大能量值出现在真实损伤位置,可以有效判断损伤位置。结果表明,在半圆形的传感器排列方式下,基于微波时间反演算法可以检测到直线形传感器排列方式下无法检测到的损伤,这是由于半圆形的传感器排列方式可以接收到侧向散射波,对散射信号的测量更加全面。这表明尽管侧向散射波的幅值较小,但侧向散射波的测量对提升检测质量具有重要的意义。

2.2 传感器数量的影响

基于上述结果可知,半圆形的传感器排列方式有助于实现对散射信号的全面测量,提升检测质量。除此之外,传感器数量也会对散射信号的测量产生一定的影响。基于图2(b)所示的模型2,改变传感器的数量,将传感器的步进角度分别设置为1°,3°,5°,7°,对应的传感器数量分别为179,59,35,24个,对应的传感器之间的距离分别为0.79,2.36,3.93,5.50 mm,分别执行相同的时间反演过程,得到的积分能量图像如图5所示。

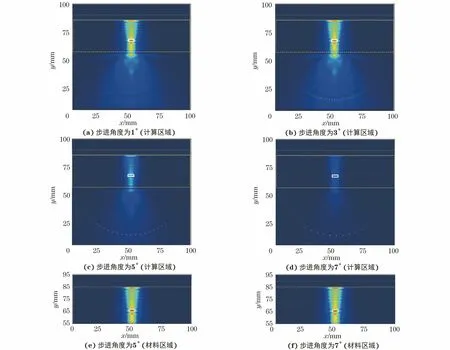
图5 不同步进角度下积分能量图像

从图5(a),(b)可以看出,最大能量位置可以指示损伤的真实位置。从图5(c),(d)可以看出,当传感器数量减少时,传感器间距增大,损伤位置累积的能量变小且小于传感器位置累积的能量,即整个计算区域的能量图像无法直观地判断出损伤位置,因此,给出在此两种传感器设置下材料区域的归一化能量图像如图5(e)和图5(f)所示。从图5(e),(f)可以看出,在对材料内部累积的能量进行归一化后,最大能量位置仍可以指示损伤的真实位置。因此,仿真结果表明在半圆形的传感器排列方式下,传感器数量的选择会对损伤位置聚焦能量的大小产生影响,选择合适的传感器数量,有利于增加损伤检测结果的直观性和鲁棒性。

为了进一步探究传感器数量和传感器间距对检测结果的影响,基于图5(c)对应的传感器设置,保持传感器数量不变,将步进角度减小为3°,即传感器间距减小,传感器以脉冲源所在位置对称分布,再次进行仿真,得到的积分能量图像如图6所示。与图5(c)中能量图像相比可知,减小传感器间距后,尽管在材料内部累积的能量在数值上明显增大,但由于缺少了对侧向散射波的接收,在损伤位置处累积的能量远小于在金属背板表面处累积的能量,此种传感器设置不再具有分辨损伤位置的能力。与图5(b)中能量图像相比可知,传感器间距不变,但减少了侧面的传感器之后,传感器无法接收到由材料表面产生的侧向散射波,能量图像中在损伤位置处累积的能量减小,最大能量位置无法指示损伤的真实位置。上述仿真结果说明减小传感器间距对材料内部区域累积的能量在数值上有一定的提升,但侧向散射波的测量对损伤位置的检测起到了更重要的作用。

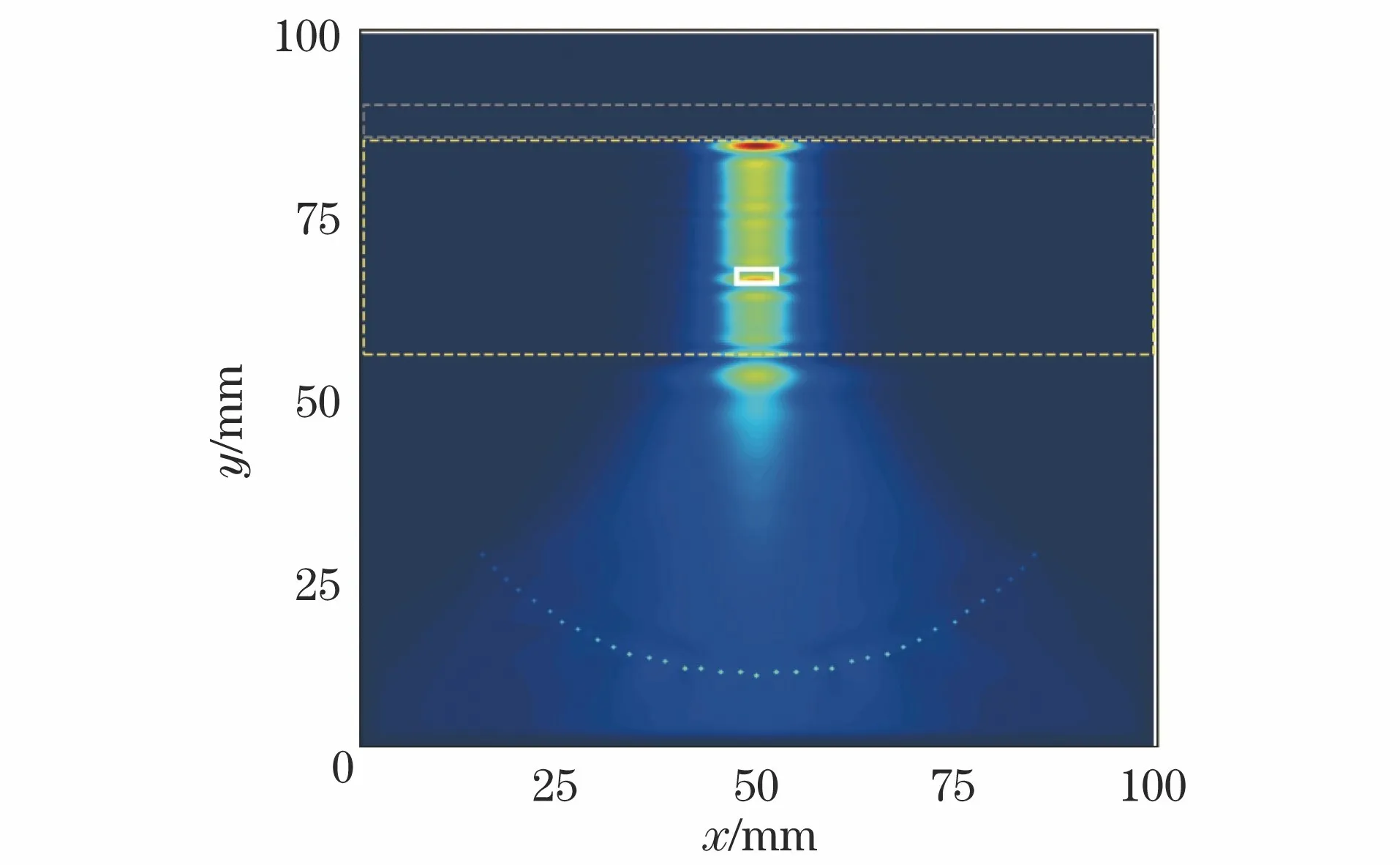
图6 传感器数量不变,减小传感器间距后的积分能量图像

综上所述,为了有效地实现复合材料内部损伤检测,需要对模型产生的散射信号进行全面地测量。不同传感器排列方式和传感器数量的仿真结果表明,侧向散射波的测量对于损伤位置处能量的聚焦起着更重要的作用。选择合适的传感器数量,对侧向散射波进行全面地测量,有助于实现高效的复合材料内部损伤检测。

3 结语

文章基于二维时域有限差分算法对复合材料模型进行了数值仿真,实现了基于微波时间反演算法的微波检测技术,结合积分能量法对材料中较小的内部损伤进行了定位,验证了所提出的复合材料无损检测技术的可行性。通过不同传感器排列方式下重构结果的对比,说明了测量侧向散射波的重要性。不同传感器数量和不同传感器间距设置下的重构结果说明了选择合适的传感器数量有利于提高检测结果的鲁棒性,并且同样表明测量侧向散射波对提升检测质量具有重要意义。