寒区隧道纵向温度场分布规律研究

王志杰, 谢盛昊, 范文昊, 王 磊, 马志富, 杨昌贤, 林 铭, 周飞聪

(1. 西南交通大学 交通隧道工程教育部重点实验室, 四川 成都 610031; 2. 西南交通大学土木工程学院,四川 成都 610031; 3. 黑龙江铁路发展集团有限公司, 黑龙江 哈尔滨 150000;4. 中国铁路设计集团有限公司, 天津 300308)

0 引言

温度是诱发寒区隧道冻害的重要因素[1-4]。一般而言,为解决寒区隧道的冻害问题,需探明其温度场的分布及变化规律。

目前,针对寒区隧道纵向温度场的分布规律已有一些研究。起初,一些学者基于二维径向温度的求解方法,结合流体力学的基本理论,建立三维纵向模型,并求解该模型的有限元公式,分析和预测围岩的冻结情况[5-6]。后来,周小涵等[7]将有限差分方法应用至隧道纵向温度场的计算中,并采用理论解析的方法探究风速、风温对隧道纵向温度场的影响。郭瑞等[8]通过设计模型试验装置研究隧道纵向温度场的特征,并通过正交试验分析得出洞口风速对寒区隧道纵向温度场的影响最大,洞口气温影响次之,隧道长度影响最小。此外,赵希望等[9]建立了考虑冰-水相变的耦合模型,分析不同风速、风向条件下隧道纵向温度场的分布,得出风速对进口段的影响远大于对出口段的影响的结果。马志富等[10]指出这是由于隧道洞口的相对高差引起的自然压差造成的。袁金秀等[11]假设隧道为圆形断面,基于热传导理论推导了隧道纵向温度场计算公式,并以此分析了列车运行时间及间隔等对隧道纵向温度场的影响。高焱等[12]进行了高速列车通过隧道的模型试验,并通过控制变量法分析了列车活塞风相关参数对温度分布的影响。Zhao等[13]探究了冬季与夏季寒区隧道纵向温度分布的差异,并提出由交通风引起的隧道内空气温度变化是瞬态的。

寒区隧道纵向温度分布较为复杂[14-16],影响因素较多,目前对于纵向温度场的计算多借助于有限元或有限差分软件,计算方法较单一。外界寒冷气流的入侵是造成寒区隧道纵向温度场变化的主要因素,故需分析其对寒区隧道纵向温度场的影响。本文对不同通风时间、等效自然风流速度及进洞风温条件下的隧道纵向温度分布及变化规律进行分析,并提出寒区隧道洞内纵向温度预测公式,以期为类似寒区隧道纵向温度场预测提供参考。

1 项目概述

本文依托工程为哈牡高速铁路鲜丰隧道,隧道进口位于黑龙江省哈尔滨市阿城区大岭乡鲜丰村正南约1 km处,出口位于利民村西北约0.6 km处。隧道起讫里程为DK62+730～DK67+075,全长4 345 m,洞身最大埋深约127.4 m。隧道线位走向大致为西北—东南走向,与冬季主风向基本一致。隧道内纵坡为8.5‰的上坡,隧道进、出口高差为36.94 m。鲜丰隧道平面位置如图1所示。

图1 鲜丰隧道平面位置图

2 寒区隧道气象要素理论

寒区隧道洞内纵向温度分布主要受洞外气象环境影响,洞外气象要素包括气温、气压、风向、风速、湿度、太阳辐射等[17]。

2.1 洞口气温确定

洞外温度直接影响寒区隧道洞口进风温度,并一定程度上间接影响隧道围岩初始温度,故其是影响寒区隧道温度场分布的重要因素。因此,本文选取洞口气温即进洞风温作为寒区隧道纵向温度场影响指标之一。根据现场温度勘测报告,采用隧道进口最冷月平均气温-18.4 ℃作为进洞风温基础参数。

2.2 等效自然风流速度

低温冷空气与隧道围岩、衬砌结构间的对流换热除受其与围岩、衬砌结构间温差的影响外,还与隧道洞内空气流速相关。隧道内空气流动主要是由隧道洞内外压强差引起的,其速度大小取决于隧道洞内外压强差。隧道洞内外的压强差受隧道洞口外的自然风速、风向、环境气压以及洞内外温度差等影响。为了探究隧道洞口外的自然风速、风向、环境气压以及洞内外温度差等与隧道洞内自然风流的关系,以等效自然风流速度即进洞风速作为寒区隧道纵向温度场另一影响指标。

隧道内形成自然风流的原因主要有风墙压差、热位差以及超静压差。

2.2.1 风墙压差

隧道洞外自然风吹向隧道洞口时,在隧道所在区域山体地形的影响下,其流动形式发生变化,洞外的动压转变为隧道迎风面的风压,而在背风面由于气流的旋转,形成负压区。迎、背风面风压可分别由式(1)和式(2)计算[18]。

迎风面风压:

(1)

背风面风压:

(2)

其中:

(3)

(4)

式(1)—(4)中:va1、va2分别为进、出口风速;α1、α2分别为进、出口风向与隧道中线的夹角;ρ1、ρ2分别为进、出口空气密度;P1、P2分别为进、出口大气压;T1、T2分别为进、出口温度;φ1、φ2分别为进、出口空气相对湿度;Psat1、Psat2分别为进、出口饱和水蒸气压力(一般不考虑);HP1、HP2分别为进、出口高程。

在分别计算隧道迎风面、背风面风压后,将其差作为风墙压差,如式(5)所示。

(5)

2.2.2 热位差

针对冬季寒区隧道,由于围岩初始地温的影响,一般隧道洞内温度会高于洞外环境温度,导致洞内空气密度相较于洞外空气密度略小,且由于隧道进出口存在高差,造成空气的浮升效应或沉降效应[18]。

具体的热位差计算公式见式(6)。

Δh=(ρ-ρ0)gH。

(6)

(7)

式(6)—(7)中:ρ0为洞内空气密度;H为隧道进、出口的高差;g为重力加速度。

2.2.3 超静压差

若大气环境中空气静止,则将隧道进出口的压差称为静压差。超静压差则是指隧道进出口的气压差与隧道进出口高差引起的气压差的差值,其计算公式见式(8)。

ΔP=P1-P2-ρgH。

(8)

2.2.4 等效自然风流速度

等效自然风流速度主要依据上述各类压差之和进行换算,总压差为风墙压差、热位差以及超静压差之和,如式(9)所示。

Pn=Δp+Δh+ΔP。

(9)

式中Pn为总压差。

依据相关规范[19]中自然风压力与隧道洞内风速的计算公式(10)可换算等效自然风流速度。

(10)

式中: ∑ζ为隧道进出口局部阻力系数之和;λ为隧道沿程阻力系数;lT为隧道长度;d为隧道断面当量直径;vn为等效自然风流速度。

综上,可根据隧道洞口风速、风向、高差等由式(11)直接计算出等效自然风流速度vn。

(11)

3 数值模型建立

3.1 模型网格及参数

鲜丰隧道为双线高速铁路隧道,通过CAD建立其三维模型,模型尺寸为4 345 m×40 m×40 m。将三维模型导入Fluent中建立三维流固耦合瞬态传热数值模型,模型由内至外依次为空气域、初期支护、二次衬砌和围岩,具体模型及划分的网格如图2所示。

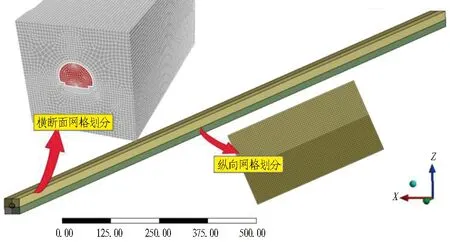
图2 隧道模型及划分的网格(单位: m)

根据相关文献[20-21]及现场试验结果,围岩及衬砌热力学计算参数选取情况见表1。此外,根据横断面设计计算Fluent中需要设置的空气相关计算参数,其具体取值如表2所示。

表1 围岩及衬砌热力学计算参数

Table 1 Thermodynamic calculation parameters of surrounding rock and lining

结构导热系数/(W/(m·℃))恒压比热容/(J/(kg·℃))密度/(kg/m3)初期支护2.409702 200二次衬砌2.409702 500围岩2.989502 600

表2 空气相关计算参数

为对通风时间、等效自然风流速度及进洞风温等要素影响下的寒区隧道纵向温度场展开研究,在隧道侧边电缆槽位置上方设置温度测线。为保持与监测位置一致,模型中温度测线设置于距二次衬砌水平距离约0.45 m处,如图3所示。该温度测线主要用于提取隧道纵向温度数据,测线上每米处设有1个测点,由此每组工况下可得4 346个纵向温度数据。

图3 温度测线布置示意图

3.2 围岩初始地温

由于山体围岩温度场具有滞后性,通过理论公式计算的结果不能完全准确地表征初始地温场,故结合数值模拟的方法确定山体初始温度场[15]。

本次计算采用瞬态传热模型,将模型在年温度周期循环100年后的温度场作为鲜丰隧道初始地温场,模型上侧边界与大气接触,其边界温度设置为随时间变化的正弦函数T(t)。结合当地隧址区的环境温度情况,累年最冷月平均气温为-18.4 ℃,累年各月平均气温为4.4 ℃,利用正弦函数对其日平均温度变化时程曲线进行拟合,拟合函数如下:

T(t)=4.4-22.8sin(2πt/365)

。

(12)

式中:T(t)为依托工程隧址区大气温度,℃;t为时间, d。

另外,由于地层深部不断传热给底部围岩,因此将底部围岩设为热流边界,取热流密度q=60 W/m2[22],方向向上。

模型荷载与边界条件设置如图4所示。

图4 模型荷载与边界条件设置

初始地温计算结果如图5所示。结合设计图纸,以隧道断面标高为基准建立纵向路径并提取纵向路径上的温度数据,绘制成鲜丰隧道纵向初始地温分布曲线,如图6所示。为便于后续精确使用隧道初始地温数据,将整体分布情况划分为5段,并采用多项式进行拟合,其中进出口的洞口段采用快速线性增长曲线来拟合。拟合温度变化曲线如图6所示。由图可知,拟合温度与模拟温度基本重合,总体上拟合效果较优。各阶段的拟合函数见式(13)。

(13)

图5 初始地温云图(单位: ℃)

式中:T′(x)为围岩初始温度,℃;x为进洞距离,m。

3.3 边界条件

结合纵断面设计图可知,隧道进口为低洞口,按第2节的压差计算分析,判断进口为洞外空气流入洞口,故将其设定为速度入口边界(velocity-inlet),并按照设计的工况来设定流入隧道内空气的风速及风温等相关参数。相对应地,在压差的作用下,隧道洞内空气由隧道出口流出,故将其设为自由出流边界(outflow)。

将3.2节计算的初始地温用C语言编译为UDF文件导入模型,赋予模型沿纵向变化的围岩初始温度。此外,模型衬砌、围岩边界及模型四周均设置为绝热边界。

3.4 基础工况参数

结合工程现场实际情况及设计说明可知,隧道走向大致为西北—东南走向,与冬季主风向基本一致,故选取进、出口风向与隧道中线夹角为0°。进、出口累年平均风速分别为3.0、2.9 m/s。故选取基础工况的环境参数如下:

隧道全长为4 345 m,隧道进、出口高程分别为206.72、243.66 m,高差为36.94 m。故隧道几何参数取值为:HP1=206.72 m,HP2=243.66 m,H=36.94 m,lT=4 345 m,d=10.322 6 m。

依据相关规范[19]中阻力系数的取值,铁路隧道进、出口局部阻力系数分别为0.5、1.0,双线铁路隧道沿程阻力系数可取0.015～0.019。故本节采用的进、出口局部阻力系数ξ1、ξ2分别为0.5、1.0,∑ξ=1.5,λ=0.018。

根据上述参数取值,按式(11)计算得到隧道等效自然风流速度vn=1.483 3 m/s。后文以vn=1.483 3 m/s,T1=-18.4 ℃为基础工况探究通风时间、等效自然风流速度及进洞风温对纵向温度场的影响。

4 现场监测

4.1 测点布置

隧道内运行设计速度为250 km/h的高速动车组。为确保运营安全,将温度测量仪器固定于侧沟盖板下方,以监测洞内温度场的变化规律,如图7所示。为便于测点定位,将测点断面选取在检查井所在断面,同时为在一定程度上反映隧道纵向温度的变化规律,选取距离隧道进口32、362、782、1 922、3 282 m位置处作为监测断面。现场测点布置如图8所示。

图7 隧道洞内温度测量仪布置示意图

图8 现场测点布置

4.2 监测结果统计

根据监测结果统计各断面的温度最大值、最小值和平均值,如表3所示。

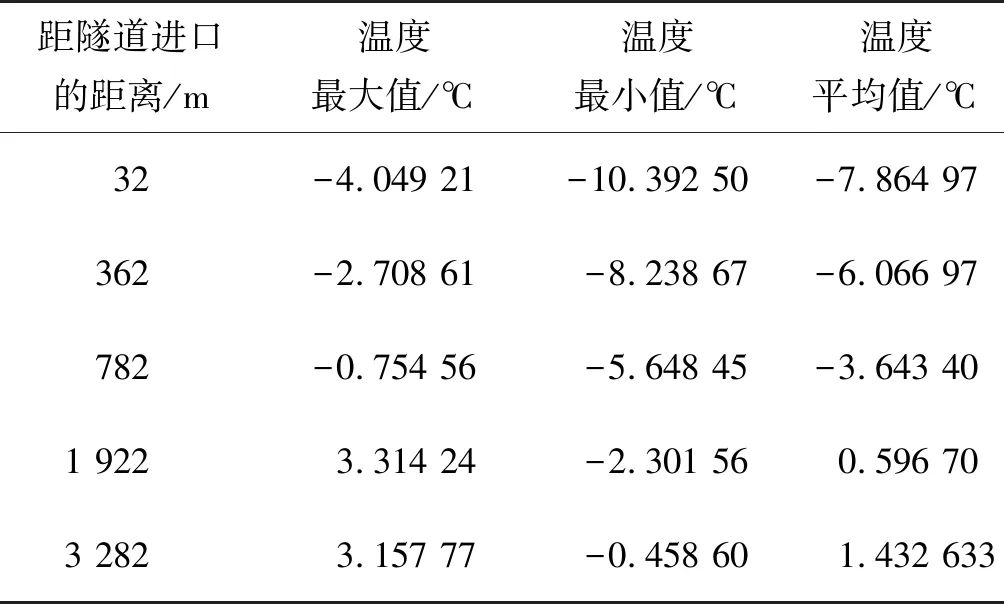
表3 洞内温度监测值

由表3可知: 在冬季,鲜丰隧道的洞内温度最大值、最小值以及平均值均随着进洞距离的增加而增大,且逐渐趋于稳定。其原因主要是外界环境空气温度较低,当其进入隧道后,与衬砌及围岩发生热交换,使得其始终处于加热状态,而进入一定距离后空气温度与衬砌和围岩温差较小,使得热交换较少,从而呈现出温度值逐渐稳定的现象。

5 寒区隧道纵向温度场影响要素分析

5.1 通风时间影响分析

为探究通风时间对纵向温度场的影响,将等效自然风流速度vn=1.483 3 m/s与隧道进口最冷月平均气温-18.4 ℃作为基础工况,计算通风时间60 d的瞬态温度场。分别提取通风时间为10、15、20、30、40、50、60 d时的隧道侧边水沟附近的温度,并绘制成随进洞距离变化的纵向温度分布曲线,如图9所示。

由图9可知,洞内温度随着进洞距离的增加呈先上升后下降的趋势,大致可分为3个变化阶段。通过对比洞内温度随不同通风时间的变化曲线可知,3个变化阶段的界限与通风时间关联不大。3个阶段具体表现如下。

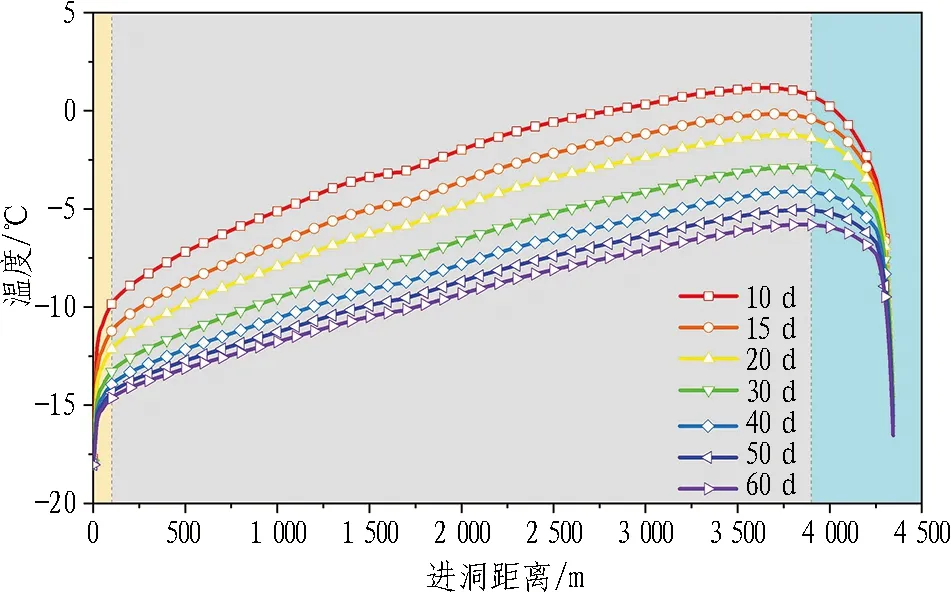
图9 不同通风时间下隧道洞内纵向温度分布曲线

1)温度快速上升阶段。在距隧道进口0～100 m处,随着进洞距离的增加,洞内温度快速增加。这主要是由于外界环境流入洞内的空气与洞内围岩的温差较大,导致二者间热量交换频繁,从而使得洞内气流温度快速上升。故随着进洞距离的增加,其上升幅度较大。以通风15 d为例,洞内温度由进口的-18.4 ℃快速上升至距洞口100 m处的-11.22 ℃,平均增加速率为0.071 8 ℃/m。

2)温度逐步上升阶段。在距隧道进口100～3 900 m处,随着进洞距离的增加,洞内温度仍呈上升趋势,但相较于第1阶段增加速度变缓。主要原因是在经过前一阶段的热量交换后,围岩与洞内空气温差相对较小,且随进洞距离增加温差进一步降低。以通风15 d为例,洞内温度由距洞口100 m处的-11.22 ℃逐步上升至距洞口3 900 m处的-0.41 ℃,平均增加速率为2.844 7×10-3℃/m。在此里程段,不同的通风时间条件下增温速率接近。

3)温度下降阶段。在距隧道进口约3 900 m至隧道出口处,随着进洞距离的增加,洞内温度受到隧道出口低温较大的影响开始呈下降趋势。以通风15 d为例,洞内温度由距洞口3 900 m处的-0.41 ℃逐步下降至隧道出口的-5.30 ℃,平均下降速率为0.011 0 ℃/m。在此里程段,通风时间越长,降温速率越快。

为进一步探究通风时间对隧道不同断面温度的影响,绘制距隧道进口32、50、200、400、800、1 600、3 200 m断面处温度随通风时间的变化曲线,如图10所示。

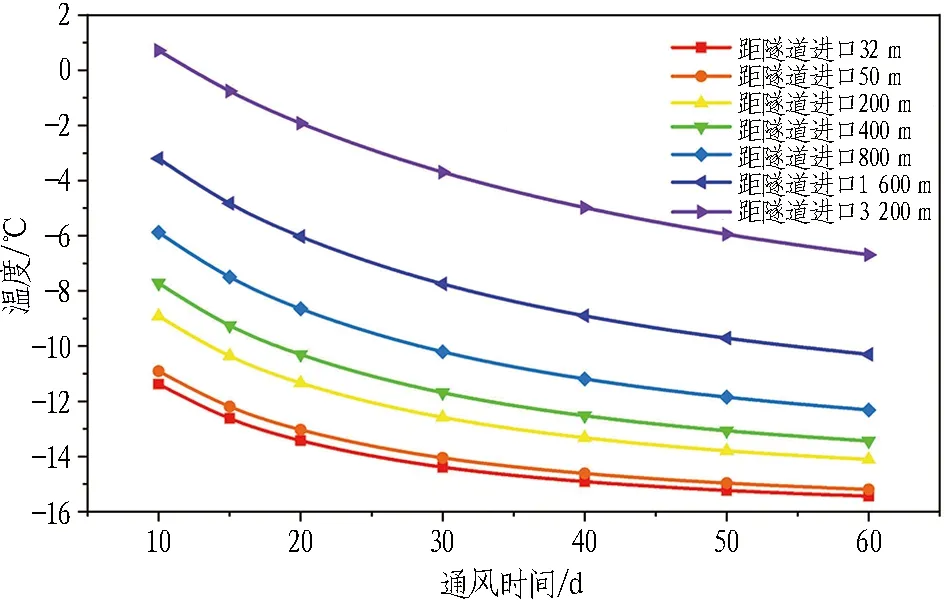
图10 隧道内不同断面的温度随通风时间的变化曲线

由图10可知,随着通风时间的增加,各个断面温度逐渐降低,变化速率逐步变缓,在60 d左右逐渐趋于稳定。对于常年处于低温环境的隧道可采用60 d的瞬态温度场进行隧道纵向温度预测。但对于依托工程,仅冬季为负温环境,且并非整个冬季都为负温状态,隧址每日温度都存在起伏变化,故采用60 d的瞬态温度场来分析温度分布情况过于保守。由于图9和图10中通风时间为15 d时断面温度的模拟值与表3中洞内温度监测数据最为接近,故可采用15 d的瞬态温度场来分析洞内温度分布情况。

5.2 等效自然风流速度影响分析

为分析等效自然风流速度对纵向温度场的影响,结合前述分析,将洞口进风温度设为-18.4 ℃,以等效自然风流速度1.483 3 m/s为基础工况,依次改变等效自然风流速度为0.5、1.0、2.0、2.5、3.0 m/s,分别计算通风15 d的瞬态温度场。提取测线温度,绘制其沿隧道纵向的变化规律,结果如图11所示。

图11 不同等效自然风流速度条件下隧道内纵向温度变化曲线

由图11可知,等效自然风流速度对隧道内的温度场具有显著影响。具体表现为: 等效自然风流速度越大,隧道内纵向温度越低。主要是由于围岩与隧道洞内空气主要通过衬砌表面的对流换热进行热量交换,故等效自然风流速度越大热量交换越频繁,隧道内温度越低。例如: 距离隧道进口100 m断面处,风速由0.5 m/s增至3 m/s时隧道洞内温度分别由-5.31 ℃降至-14.11 ℃,降低了8.80 ℃;距离隧道进口3 900 m断面处,风速由0.5 m/s增至3 m/s时隧道洞内温度分别由3.97 ℃降至-5.55 ℃,降低了9.52 ℃。

此外,由图11可知,洞内温度随着进洞距离的增加呈现先上升后下降的趋势,变化曲线大致可分为3个变化阶段。为更有效地表征寒区隧道洞内纵向温度分布规律,对各等效自然风流速度下的纵向温度变化曲线按3阶段进行分段数值拟合,拟合函数系数与等效自然风流速度之间基本符合指数函数变化形式,故采用ExpDec1模型对其进行回归分析,最终拟合结果见式(14),拟合函数中各系数取值见表4。

(14)

表4 拟合函数系数取值

5.3进洞风温影响分析

为分析进洞风温对纵向温度场的影响,将进洞风温设为-18.4 ℃,以等效自然风流速度1.483 3m/s为基础工况,依次改变进洞风温分别为-20、-15、-10、-5 ℃,分别计算通风15d的瞬态温度场。提取测线上的洞内温度,绘制其沿隧道纵向的变化曲线,结果如图12所示。

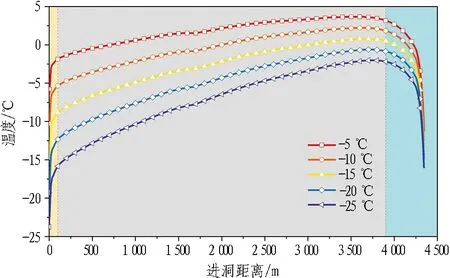
图12 不同进洞风温条件下隧道内纵向温度变化曲线

由图12可知,进洞风温对隧道纵向温度分布具有直接影响。具体表现为: 隧道进口空气温度越高,隧道洞内纵向温度越高。主要由于流入洞内空气的温度升高,致使围岩与空气温度差值减小,使得围岩与隧道洞内空气对流换热减少,降低了围岩向洞内的热量传递。例如: 距隧道进口100 m断面处,进洞风温由-25 ℃增至-5 ℃时隧道内温度分别由-15.83 ℃升至-1.86 ℃,升高了13.97 ℃;距隧道进口3 900 m断面处,进洞风温由-25 ℃增至-5 ℃时隧道洞内温度分别由-2.18 ℃升至3.19 ℃,升高了5.37 ℃。对于出口段,隧道内温度更多是受围岩温度的影响,隧道内空气与围岩进行热量交换,在出口数米内受出口低温影响会出现显著的温度骤降现象。

此外,由图12观察到各工况下纵向温度变化曲线间隔大致相近。为验证其差值是否相同,对各相邻2组工况纵向温度作差,并绘制其与进洞距离的关系曲线,结果如图13所示。

图13 相邻工况纵向温度差

由图13可见,绘制的4条曲线近乎重合,故各相邻工况温差近乎相同,即相同进洞温度变化引起的洞内温度变化相同;且由曲线变化特征上来看,随着进洞距离的增加,温差逐渐降低。为有效表征进洞风温对寒区隧道纵向温度场的影响,对相邻工况(即进洞空气温度差为5 ℃)引起的同一断面纵向温度差随进洞距离的变化曲线采用ExpDec3模型进行拟合,拟合公式如式(15)所示,其相关系数为0.999 9,拟合效果很好。

0.145 6。

(15)

故相对于基础工况,结合式(15)可得单位进洞空气温度变化引起的洞内各断面温度变化函数ΔTT(x)=ΔTT-5(x)/5,具体计算公式如式(16)所示。

0.029 1。

(16)

6 寒区隧道洞内纵向温度预测公式

根据第5节所述内容,整理可得以进洞距离、等效自然风流速度及进洞风温为变量的寒区隧道洞内纵向温度预测公式,如式(17)所示。

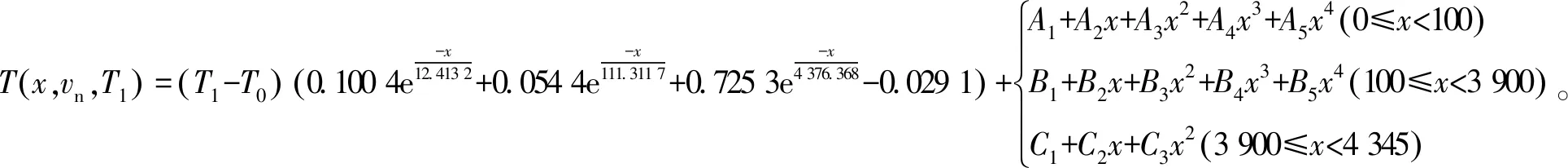
(17)

式中:T(x,vn,T1)为隧道内温度;x为进洞距离;vn为等效自然风流速度,计算见式(11);T1为进洞风温;T0为基础工况进洞风温,取-18.4 ℃。

7 结论与讨论

本文借助Fluent软件建立了寒区隧道三维流固热耦合模型,并建立了进出口隧道高差,洞口风速、风向等要素与隧道洞内等效自然风流速度的关系,以此分析不同通风时间、等效自然风流速度及进洞风温条件下的隧道洞内纵向温度分布及变化规律。基于回归分析方法,提出以进洞距离、等效自然风流速度及进洞风温为变量的寒区隧道洞内纵向温度预测公式。具体结论如下。

1)寒区隧道内纵向温度随着进洞距离的增加呈先上升后下降的趋势,变化曲线大致可分为温度快速上升、温度逐步上升、温度下降3个阶段。

2)随着通风时间的增加,隧道内各个断面的温度逐渐降低,且在60 d左右逐渐趋于稳定。对于常年处于低温环境的隧道可采用60 d的瞬态温度场进行隧道纵向温度预测。但若实际工程并非始终处于负温状态,温度存在起伏变化,则可采用15 d的瞬态温度场来分析温度分布情况。

3)等效自然风流速度对隧道洞内温度场具有显著影响,等效自然风流速度越大,围岩与隧道洞内空气间热量交换越频繁,隧道洞内纵向温度越低。

4)进洞风温对隧道洞内温度场具有直接影响,随着进洞风温的增加,围岩与隧道洞内空气间热量交换相对减少,使得围岩向洞内传递热量的效率降低。另外,随着进洞距离的增加,进洞风温对隧道纵向温度场的影响逐渐减小。

5)隧道洞内纵向温度3个变化阶段函数的各系数与等效自然风流速度之间符合指数函数变化形式,因此以单位进洞风温变化引起的洞内温度变化式作为修正项,提出以进洞距离、等效自然风流速度及进洞风温为变量的寒区隧道洞内纵向温度预测公式,为隧道洞内纵向温度预测及保温设防提供参考。

对于寒区隧道纵向温度场的研究,本文在同一组工况中将等效自然风流速度与进洞温度控制为定值,实际上其单日内会存在起伏变化,后续研究中可进一步缩短数值计算时间步长,针对时刻变化的风速、风温进一步探究。