基于小波-云模型的地下洞室围岩变形监控指标拟定

2023-11-22吕小龙景来红王玉杰翟利军杨喜清

水力发电 2023年11期

吕小龙，景来红，王玉杰，翟利军，杨喜清

(1.黄河勘测规划设计研究院有限公司，河南郑州 450003；2.水利部黄河流域水治理与水安全重点实验室(筹)，河南郑州 450003；3.中国水利水电科学研究院岩土工程研究所，北京 100048)

0 引言

监控指标是实时掌握工程运行状态、保障人员财产安全的重要依据。由于大型地下洞室群地质条件复杂，围岩稳定受洞室规模、布置形式、岩体质量等众多因素影响，现行规范中的围岩变形监控指标较为单一且模糊[1-3]，不同工程规模和工程地质下的实践表明，其实用性不理想。

目前，国内学者对监控指标的研究主要集中在重力坝变形、土石坝渗流等方面。舒光学等[4]引入基于极值理论的POT(Peaks Over Threshold)模型，对大坝监控数据的尾部特征拟合结果表明，在采样数据较少的情况下，POT模型具有更高的精度。赵鲲鹏等[5]采用经验模态分解滤波方法对原始数据降噪，然后采用云模型拟定大坝安全监控指标。肖磊等[6]采用最大熵法和云模型法拟定了大坝运行期变形监控指标，探讨了异常概率与云模型弱外围元素对定性概念贡献率之间的联系。建剑波等[7]建立了基于日变化速率的改进云模型，对河口村水库的监测数据进行异常识别。上述成果为实际工程运行状态评估提供了重要依据。

目前，在地下洞室围岩变形监控指标拟定方面，主要采用传统的置信区间法、典型小概率法等传统方法，存在含噪声数据精度低、人为假定概率密度函数等不足。针对这一问题，本文建立一种基于小波-云模型的监控指标拟定方法，应用于某大型地下洞室工程，并与传统的典型小概率法拟定指标进行对比分析，验证了所述方法的合理性和可行性。

1 基于小波-云模型的监控指标拟定方法

受环境波动、仪器精度等因素影响，现场监测数据普遍含有噪声。通常，真实信号主要分布于数据的低频区域，局部细节信息和噪声则混杂在高频区域。小波变换通过伸缩、平移运算对数据逐步进行多尺度细化，最终实现高频区域时间细分、低频区域频率细分，可聚焦于数据的任意细节。小波降噪基于小波变换多分辨分析的特性，根据噪声与真实信号在不同频带上的小波分解系数具有不同强度分布的特点，将各频带上噪声对应的小波系数去除，保留原始信号的小波分解系数，然后对处理后的系数进行小波重构，得到纯净数据。小波降噪既能降低数据噪声，又能保留数据的局部细节信息，可用于监控指标拟定前的数据预处理。

云模型充分考虑数据的随机性和模糊性，无需事先设定数据的概率分布函数，即可基于原型监测数据拟定监控指标[8-15]。首先，采用逆向云发生器，计算数据样本的期望Ex、熵En和超熵He，实现数据特征的定性；然后，通过正向云发生器生成云滴群，实现数据特征的定量；最后，基于云模型的“3En规则”确定监控指标。本文先采用小波降噪对监测数据进行预处理，再采用云模型拟定监控指标。基于小波-云模型拟定监控指标流程见图1。具体实施步骤如下：

(1)选择小波基和分解层次，对含噪声监测数据进行多尺度分解。

(2)对高频系数进行阈值量化，对于从1到N的每一层，选择1个阈值，并对这一层的高频系数进行软阈值化处理。其中，N为小波分解层数。

(3)根据小波分解的第N层的低频系数和经过修改的从第1层到第N层的高频系数，采用小波逆变换重构真实数据系列。

(4)采用逆向云发生器，根据下式计算数据样本的期望Ex、熵En和超熵He，即

(1)

(2)

(3)

(4)

(5)

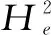
(6)基于云模型的“3En规则”拟定监控指标。论域中定性概念贡献率较大的云滴群有99.7%分布在[Ex-3En，Ex+3En]范围内，此区间以外的云滴对定性概念的贡献率基本可以忽略。因此，若监测值位于[Ex-3En，Ex+3En]外侧，表明数据异常。基于“3En规则”，即可确定监控指标。

2 工程实例

某大型地下洞室群布置于相对完整的花岗岩岩株内，最大埋深达730 m，主洞室为城门洞形，其中上部起拱跨度49 m，起拱高度27 m，下部水池边墙高度44.9 m。工程具有大埋深、大跨度、高边墙的特征。基于永临结合原则，在施工阶段布置了系统的监测项目。典型监测项目见图2。

图2 典型监测项目

由于主洞室跨度远超常规的30 m量级，顶拱围岩稳定是工程重点关注的问题。下部边墙开挖后，采用60 cm厚的混凝土衬砌，且在后续运行阶段，水池内充满水，对边墙稳定有利。因此，选取主洞室顶拱中心BX-10的变形速率作为监控指标拟定对象。

2.1 基于小波-云模型的监控指标拟定

(6)

图3是BX-10在不同小波阶数和分解层数条件下的信噪比。从图3可知，db7小波的信噪比最高，且随着分解层数增大，信噪比快速收敛。由于较大的分解层数有利于信号和噪声的分离，同时兼顾计算效率，综合分析选用db7进行4层小波分解，对分解后的高频部分采用软阈值去噪，去噪重构后的变形速率和原始监测数据见图4。图4中，以围岩向临空面变形为正，向岩体内部变形为负。从图4可知，降噪后数据与原始监测数据趋势一致，且降噪后曲线更加平滑。

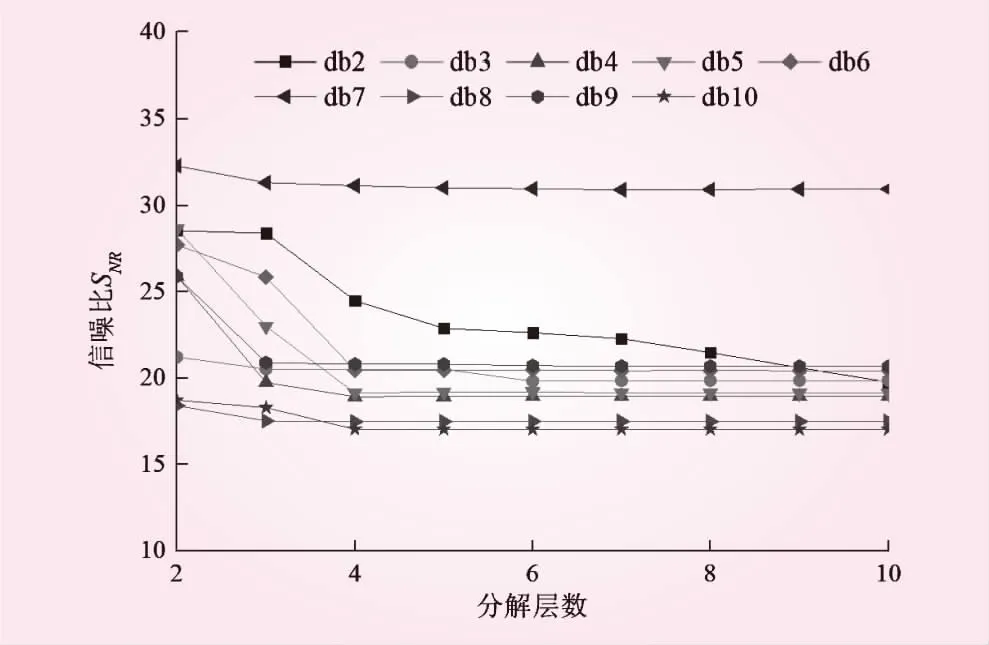
图3 小波降噪参数敏感性分析

图4 原始监测数据与去噪重构数据对比

采用逆向云发生器，求取降噪后围岩变形速率的数字特征Ex=0.0171、En=0.0497、He=0.0212。然后，根据云滴对定性概念的贡献度，基于“3En准则”确定围岩变形速率的安全区间为[-0.132，0.166]。因此，根据上述计算成果，试验大厅顶拱中心BX-10处围岩向临空面的变形速率不宜超过0.166 mm/周，向岩体内部的变形速率不宜超过0.132 mm/周。

2.2 基于典型小概率法的监控指标拟定

现场监测资料表明，试验大厅开挖衬砌完成后，围岩位移呈正负波动性变化，故选取每月的最大和最小变形速率作为典型效应量。BX-10变形速率极值统计见表1。

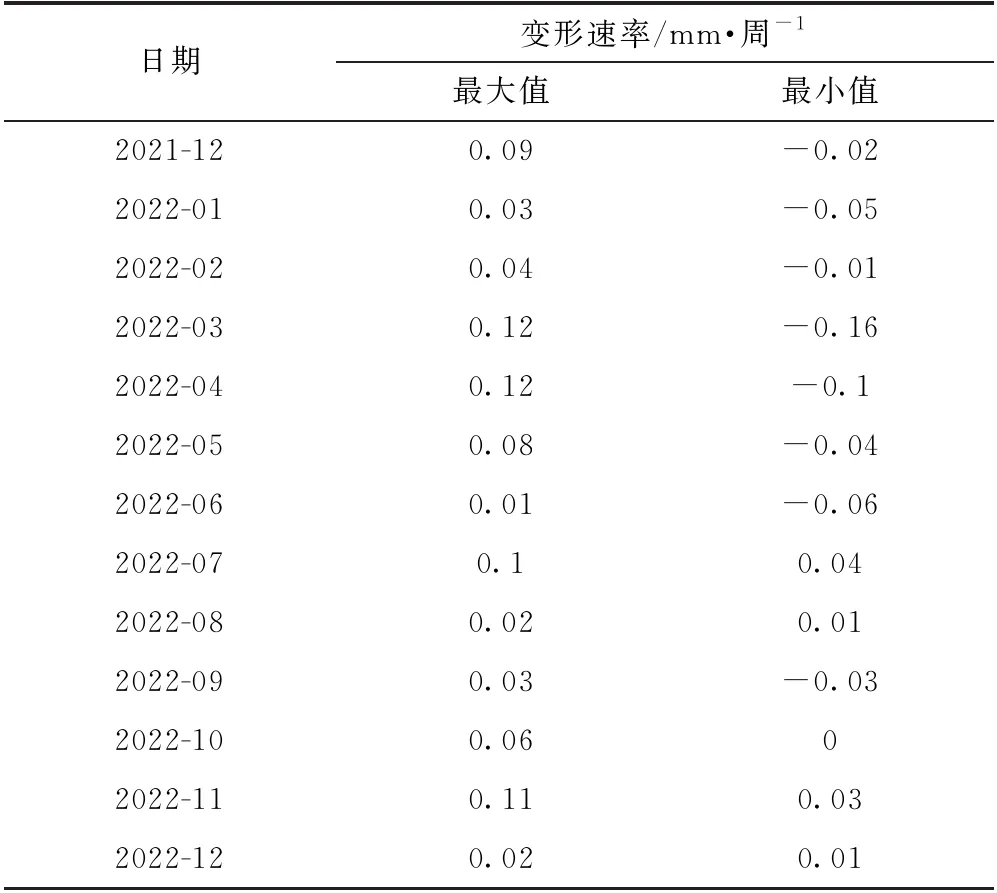
表1 BX-10变形速率极值统计

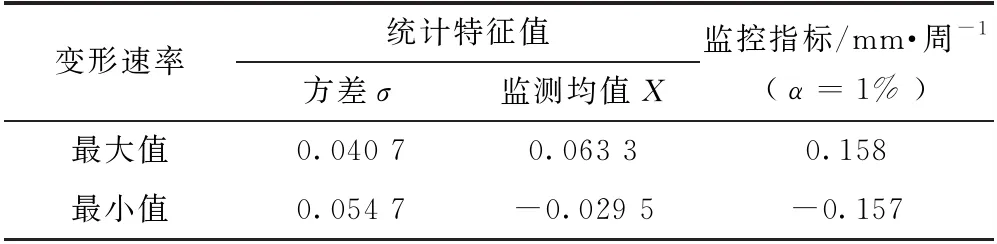
根据K-S法检验，BX-10的最大和最小变形速率均服从正态分布。令Xm1和Xm2分别为监控指标的极大和极小值，当X>Xm1或X

(7)

(8)

表2是由BX-10实测资料确定的统计特征值和监控指标。从表2可知，BX-10处围岩向临空面的变形速率不宜超过0.158 mm/周，向岩体内部的变形速率不宜超过0.157 mm/周。

表2 BX-10统计特征值和监控指标

2.3 2种拟定方法对比

地下洞室在长期运行过程中，围岩主要呈现流变特性，即在地应力作用下，围岩向临空面持续变形。由于本工程的围岩质量高，地应力水平适中，流变作用较微弱，但在流变和环境随机波动影响下，围岩向临空面方向的监控指标应大于向岩体内部的监控指标。基于典型小概率法拟定的监控指标最大值和最小值基本相同，该结果与基本力学原理相悖，其合理性存疑。

基于小波-云模型拟定的监控指标，不仅满足围岩向临空面方向变形大于向岩体内部变形的基本要求，且充分考虑了数据噪声的影响，亦无需事先假定样本的概率密度函数，计算结果更具客观性和合理性。