基于云模型的深圳市降水时空分布研究

2023-11-22梁巧茵李帅杰张明凯

水力发电 2023年11期

梁巧茵，李帅杰，孙翔，张明凯

(1.深圳市水务规划设计院股份有限公司，广东深圳 518001；2.中规院(北京)规划设计有限公司，北京 100044；3.哈尔滨工业大学环境学院，黑龙江哈尔滨 150090；4.南方科技大学环境科学与工程学院，广东深圳 518055；5.北京协同创新研究院，北京 100094)

0 引言

降水的丰枯变化将直接影响河道水库的水位及水资源的合理开发利用，也是直接影响洪涝及干旱风险的因素。降水的时空分布规律研究是一项基础又重要的工作，是深入认识水循环、合理利用雨水资源的先决条件[1]，而合理利用雨水资源可以有效减少洪涝灾害造成的损失，缓解用水矛盾，促进城市可持续发展。

深圳市作为粤港澳大湾区的核心城市，其降水时空变化特征对粤港澳大湾区的防洪抗旱减灾及区域可持续发展，建成世界级一流湾区具有重要的影响。目前针对深圳市降水时间分布及变异规律的研究主要采用小波分析法、累积距平法、Mann-Kendall检验法、有序聚类法等[2-4]，研究降水空间分布的方法主要为经验正交函数(EOF)分解法[5]，这些方法的不足之处均在于难以实现对降水分布的均匀性与稳定性进行量化。

作为可以实现定性定量转换的工具，云模型在随机变量的时空分布特征研究中应用广泛。刘德地等[6]利用云模型对广东省东江流域57个站点45 a的降雨时空分布进行研究；詹存等[7]利用云模型对青藏高原江河源区7个气象站点53 a的降雨时空分布进行分析；刘睿等[8]采用Mann-Kendall检验与云模型相结合的方式，分析了金沙江流域29个气象站点60 a的降水时空分布特征；孙朋等[9]采用云模型对安徽省14个气象站点60 a的潜在蒸散量、降水量和干湿指数的时空分布特征进行了研究。关于云模型的特征分析表明，云模型是研究降水等水文气象要素变化时空分布规律和机理的新途径，是定量分析降水时空分布均匀性与稳定性的行之有效的方法。

本文从时间尺度和空间尺度上，利用云模型方法，并结合传统的趋势分析与突变检验法等对深圳市的降水分布特征进行研究，以期深入了解降水变化规律，为深圳市合理配置水资源、防汛抗旱、应对洪涝灾害风险等提供决策依据，对提升城市韧性、促进城市可持续发展也具有重要的意义。

1 研究区域和资料

1.1 研究区域概况

深圳市位于广东省沿海地区，珠江三角洲东岸，北与东莞、惠州接壤，南隔深圳河与香港相邻，西濒珠江口与伶仃洋，东临大鹏湾与大亚湾。深圳市呈东西长、南北窄的狭长形，位于北纬22°27′～22°52′及东经113°46′～114°37′之间，陆域面积约1 997 km2，下辖9个行政区及1个新区(不含深汕特别合作区)。深圳市属南亚热带海洋性季风气候区，雨量充沛，多年平均降水量1 777 mm，夏季多雨，冬季少雨。降水年际及年内变化较大，时有干旱及洪涝灾害发生。

1.2 数据资料

根据深圳市地形地貌及水系发育情况，分为茅洲河、珠江口、观澜河、深圳湾、深圳河、龙岗河、坪山河、大鹏湾、大亚湾等9大流域。本研究选取深圳市11个雨量观测站1960年～2020年共61 a长系列的逐月降水量资料，基本覆盖了深圳市9大流域，站点空间分布比较均匀，代表性较好，雨量站空间分布见图1。降水数据来源为《深圳市水文年鉴》，经过基本的质量控制，包括可靠性及一致性审查，时间序列较长，部分测站缺测的数据根据邻近站点进行插补延长，连续性及完整性可以满足研究的需要。

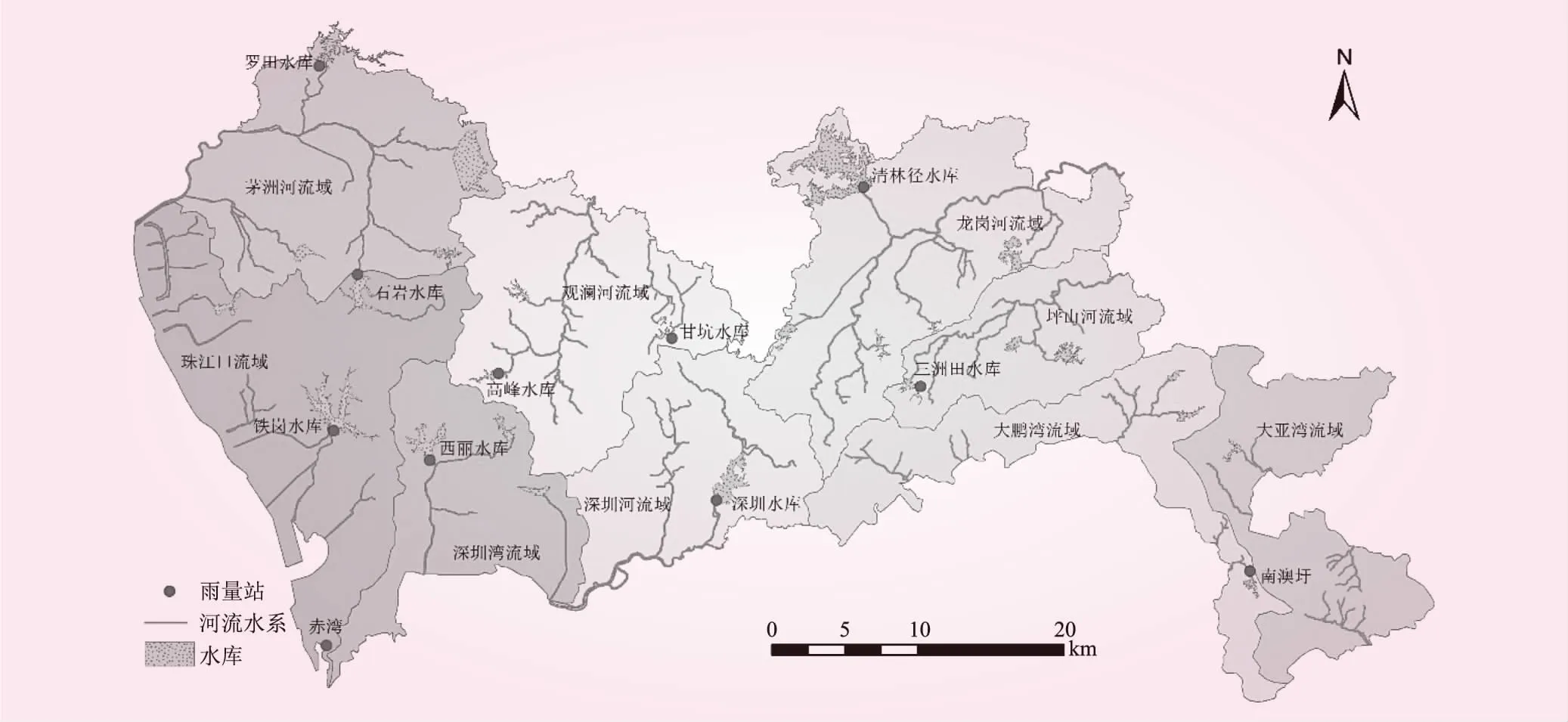
图1 深圳市代表性雨量站点分布

对深圳市降水量的时间分布特征进行云模型分析时，以各个雨量观测站i时段的降水量算术平均值Pi作为深圳市i时段的面降雨量，公式为

(1)

对深圳市降水量的空间分布特征进行云模型分析时，以各时段j雨量观测站的降水量算术平均值Pj作为j雨量观测站在该时段的平均降水量，公式为

(2)

式中，r为各时段的年份数。

2 研究方法

2.1 云模型

云模型的数字特征包括期望Ex、熵En和超熵He。期望即平均值，熵表征离散程度及不均匀程度，超熵即熵的熵，反映云的厚度，表征稳定性。

云滴作为云的组成要素，可对定量数据进行定性描述，其生成可通过云发生器实现。云发生器分为正向云发生器和逆向云发生器，正向云发生器通过云模型的数字特征产生云滴；而逆向云发生器则是通过给定的云滴求出云模型的3个数字特征。正向及逆向云发生器的具体算法步骤可参考文献[7，10-11]。

基于一阶绝对中心矩的单步式的逆向云算法，在实际计算中有可能出现超熵为虚数，因此许昌林和王国胤[12]提出了多步式的逆向云变换算法。多步式的逆向云变换算法在计算过程中增加了对样本的随机抽样分组，具体如下：

(1)输入。n个云滴xi，i=1，2，…，n。

(2)输出。反映定性概念的数字特征，即期望Ex，熵En，超熵He。

具体步骤及核心算法如图2所示。

图2 核心算法程序

多步式的逆向云变换算法降低了超熵出现负数的概率，且基本接近初始概念，不发生飘移，稳定性较强[13-14]。本文随机抽取10组样本，并循环1 000次，其计算结果作为最终的熵和超熵取值。

2.2 滑动t检验法

根据相关研究[15-17]，检测突变点的方法通常有Mann-Kendall法、低通滤波法、滑动t检验法等。低通滤波法不能确定具体的突变时间；Mann-Kendall法中不是所有序列交叉点均为突变点，需要结合其他方法去除其中的杂点从而进一步确定突变点。本文采用滑动t检验进行突变点判定，滑动t检验的统计量T计算公式为

(3)

(4)

3 降水时空分布特征分析

3.1 降水时间分布特征分析

3.1.1 年内变化特征

对深圳市月降水资料进行统计分析，见图3及图4。深圳市年内降水分配不均匀，表现为夏季高，冬季低的季节特征。由图3可知，深圳市降水年内分布特征为双峰型，存在6月和8月2个峰值，2个峰值之间出现相对低谷，与珠江流域的降水年内变化规律一致[18]。由图4可知，1960年～2020年间，深圳市多年月平均降水量占比最大的为6月份，占多年平均降水量的4.5%～48.4%，平均占比17.9%；最小为12月份，占多年平均降水量的0～10.4%，平均占比1.5%。

图3 深圳市月平均降水量

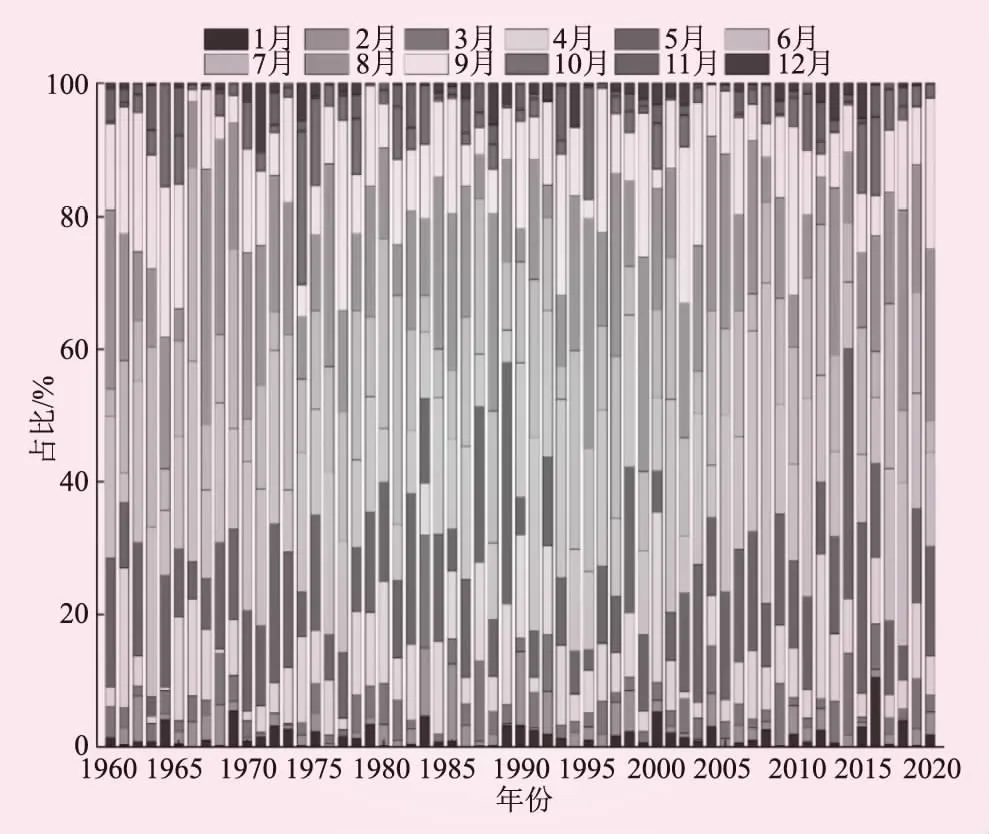
图4 深圳市降水量年内变化

采用多步还原逆向云变换算法计算深圳市1960年～2020年各月及全年降水量，得到各时段的云模型数字特征值，见表1。采用正向云发生器分别绘制出各月降水量的隶属云图，见图5。

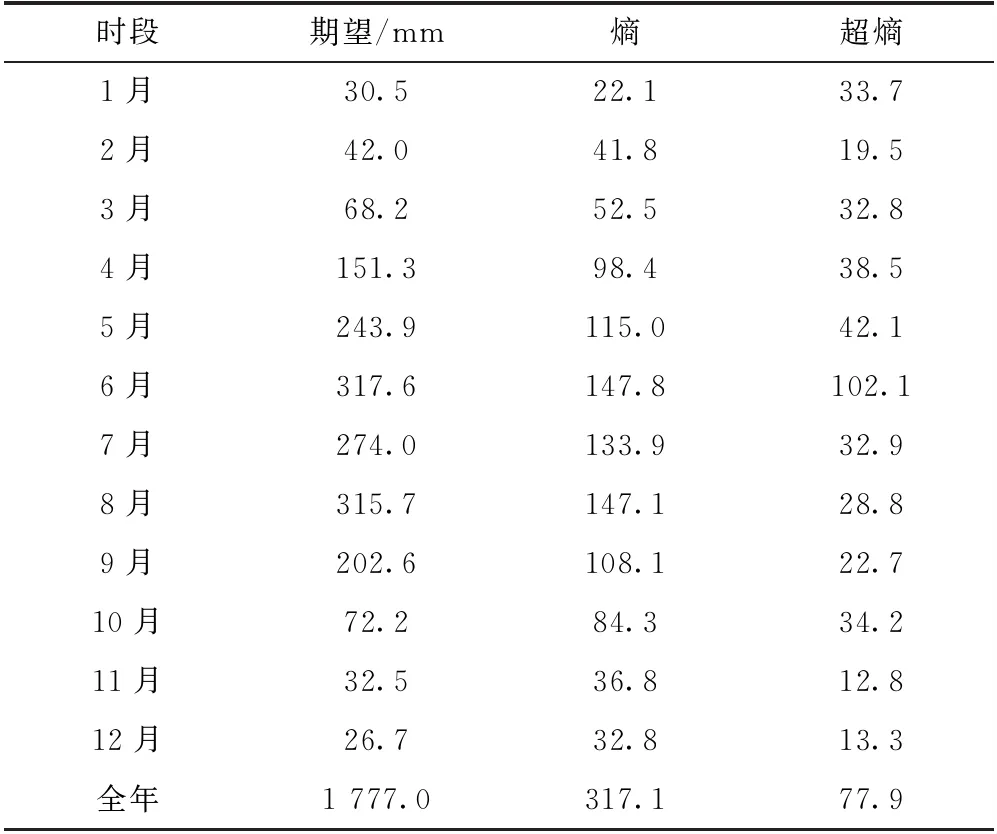
表1 深圳市各月降水量云模型数字特征值

图5 深圳市1960年～2020年各月降水量隶属云图

云模型中期望反映云滴的重心，表示降水量大小的平均值；熵体现降水量的不均匀程度，即相对于均值的离散，熵值越大表示降水分布越不均匀；超熵是熵不确定性的度量，反映不均匀性的稳定性，其值越大，即云的厚度越大，隶属度的随机性也增大，表示降水越不稳定。从表1和图5可以看出：

(1)降水量年内分布不均匀，主要集中在汛期(4月～9月)，汛期降水量占全年降水量的85%左右，远大于非汛期(10月～次年3月)。6月的降水量最大，8月次之；11月～次年2月降水量相近且较小。

(2)汛期的熵值较大，表明汛期尤其6月～8月降水的离散程度大，不均匀程度高。非汛期的熵值较小，降水量分布较为均匀。从全年的尺度看，降水量离散程度最大，取值范围广，水资源管理难度较大。

(3)从各月的超熵可以看出，6月的超熵值最大，云层厚度大，稳定性低，不确定性高。11月、12月及2月的超熵较小，云层厚度较小，说明这些月份的降水分布较为稳定。

云模型不仅可以对降水时间序列进行定性分析，反映出降水时间序列的不均匀性，隶属云图还能清晰直观地看出各月降水的稳定性程度。云模型能对降水不均匀性的稳定性进行定量分析，是研究降水等水文要素在时间上变化特征的有效方法。

3.1.2 年际变化特征

1960年～2020年深圳市降水量年际变化明显，多年平均降水量为1 777.0 mm；年降水量最大的年份为2016年，降水量2 508.0 mm，年降水量最小的年份为1963年，降水量858.3 mm，前者为后者的2.92倍，两者相差1 649.7 mm，深圳市降水量年际变化趋势见图6。从图6可以看出，深圳市全年降水量总体上呈增加趋势，年降水量按27.9 mm/(10 a)增加。

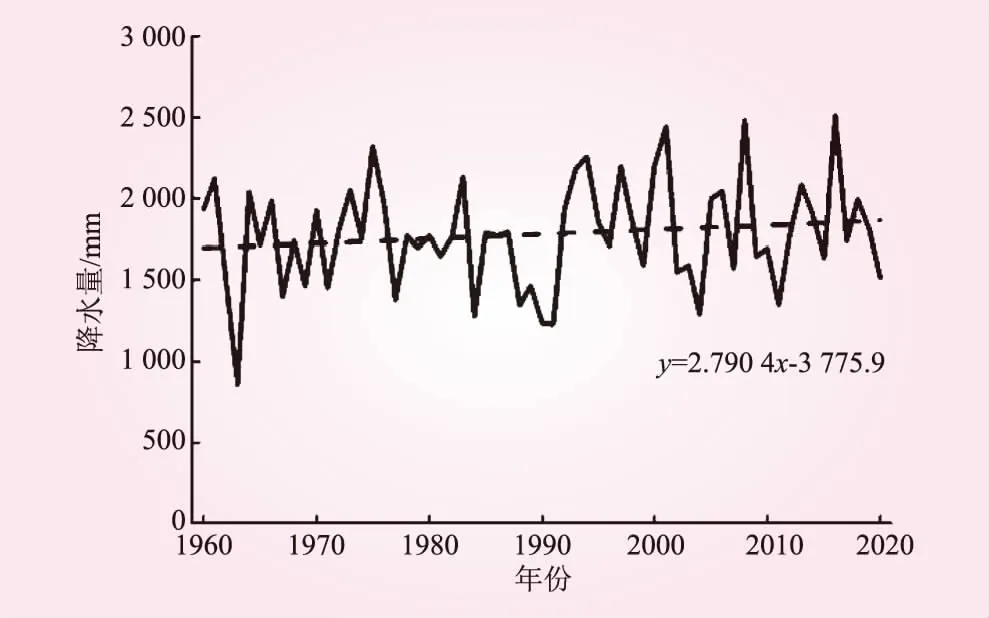
图6 深圳市降水量逐年值及线性趋势

进一步采用距平百分率分析降水量的年际变化特征，深圳市年降水量距平百分率见图7。

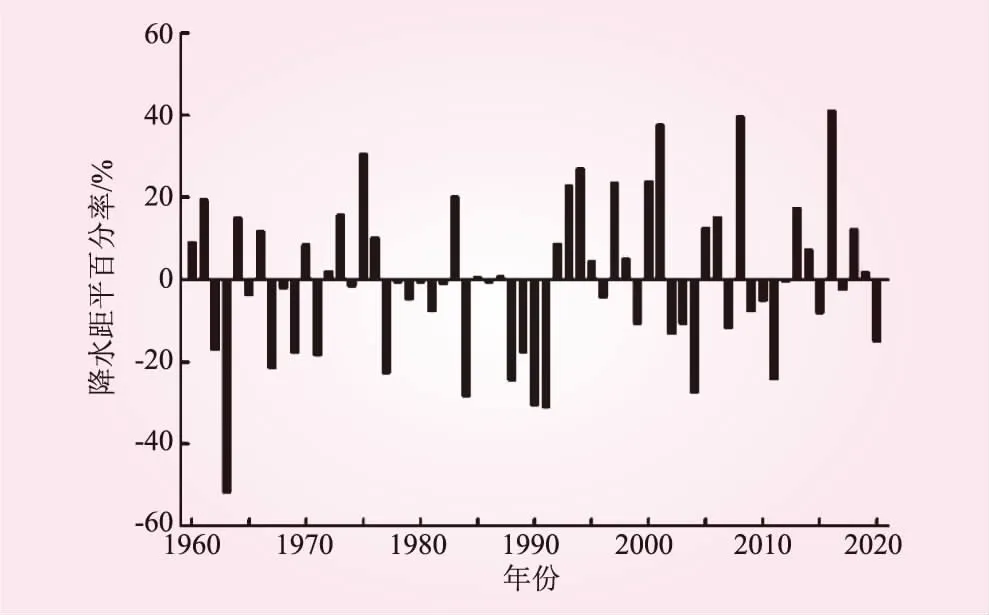
图7 1960年～2020年深圳市降水量距平百分率

从图7可知，深圳市年降水量的正距平值介于10.2～731.0 mm之间，负距平值介于-918.6～-3.6 mm之间，降水量距平百分率在-51.7%～41.1%之间。由此可以看出，深圳市降水量的年际变化差异比较大，变化幅度也较大。

为了更进一步分析比较降水在时间序列的变化特征，基于滑动t检验对年降水量做突变分析。对滑动t检验的时间步长取值为5，显著性水平取值为0.05，计算T值并绘制滑动t检验图，见图8。

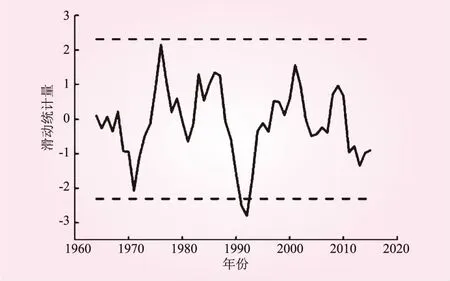
图8 年降雨量突变检验(滑动t检验)

从图8可知，1992年的T值为-2.80，属于极小值，超过了0.05显著水平对应的临界值-2.31，因此认为1992年极有可能是突变年。分别计算1960年～1991年和1992年～2020年的年平均降水量，分别为1 688.5 mm和1 874.5 mm，相差186 mm，差别较大。综上确定，1992年为降水突变年。

降水的变化可能与城市化进程有关，城市化是土地利用变化的一种表现形式，其导致的下垫面变化、产业变化对降水具有一定的影响。已有研究表明[19-20]：城市化后期与前期相比，降水总量、降水日数等指标均发生明显变化；城市化还能通过下垫面及降水的变化对水文过程产生影响，增加洪涝风险。1992年深圳市扩大特区范围，原宝安县分成宝安、龙岗两区，时间节点与降水变化的突变点基本吻合[5]。

3.2 降水空间分布特征分析

Kriging插值方法以空间结构分析为基础进行估值，能消除采样不均造成的误差，且接近实际，在小区域的研究中应用广泛[21]。本文根据深圳市11个代表性雨量站点1960年～2020年的逐月降水资料，计算出各站点多年平均降水量的云模型数字特征，采用Kriging插值法对这些数字特征进行空间插值，得到降水要素在深圳市的空间分布，见图9。

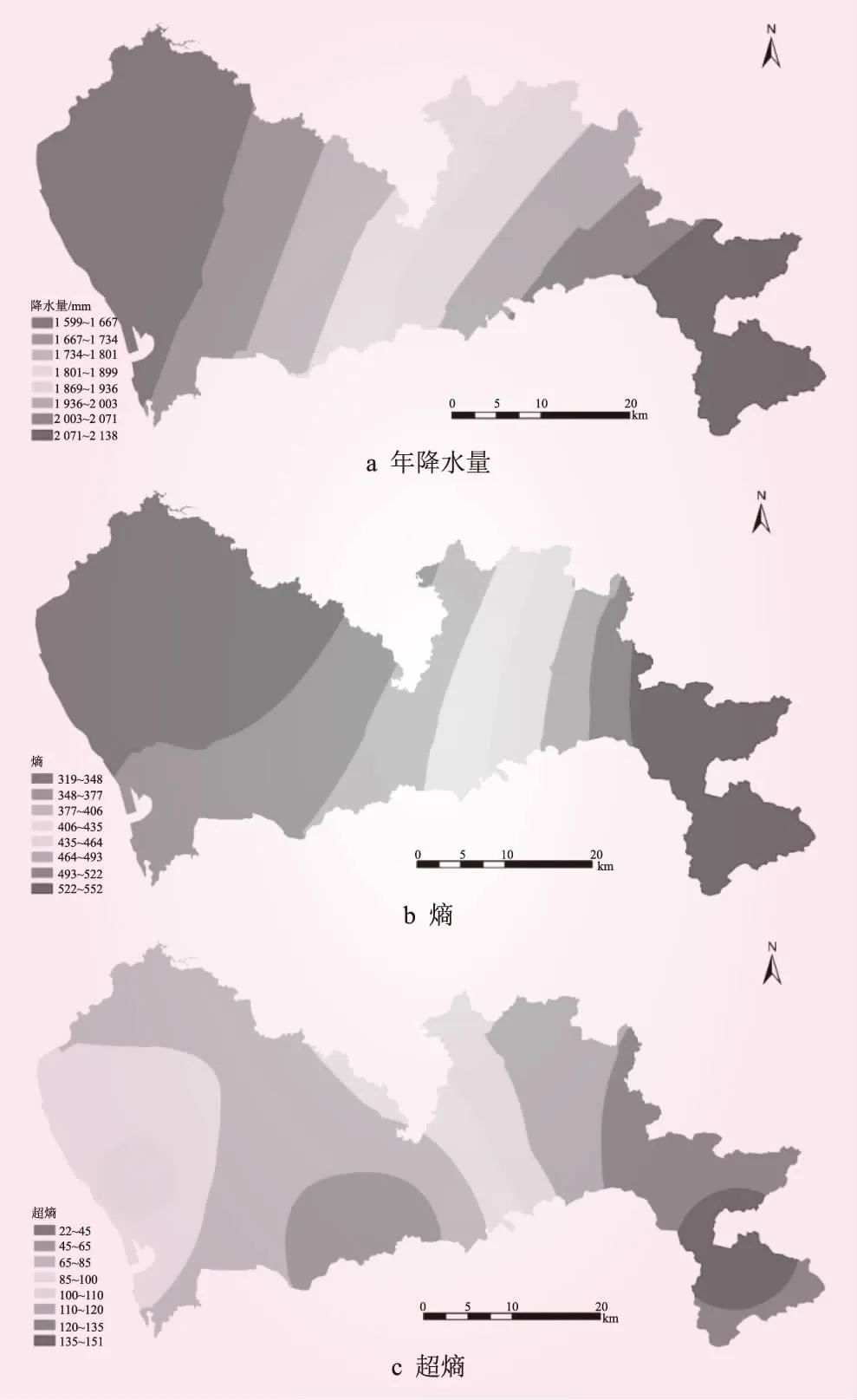
图9 深圳市1960年～2020年降水特征空间分布

从图9可知，深圳市降水量及其熵值的空间分布趋势相似，均为从东南向西北递减。超熵的空间分布规律为东部处于高值区域，中部为低值区域。整体上看，深圳市东部的大亚湾流域、大鹏湾流域年降水量最多，降水分布最不均匀，其不均匀性最不稳定；西部的茅洲河流域及珠江口流域降水量最小，降水分布比较均匀；中部的深圳河流域，超熵最小，降水最为稳定。

为进一步探讨年降水空间分布的演变趋势，根据突变分析将年降水变化特征分为1960年～1991年、1992年～2020年2个时段，并与1960年～2020年进行对比分析。深圳市不同时段年降水空间分布云模型的数字特征及隶属云图，分别见表2及图10。

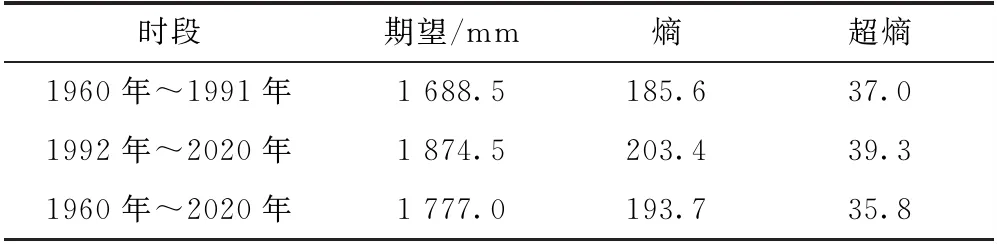
表2 深圳市年降水量空间分布云模型的数字特征

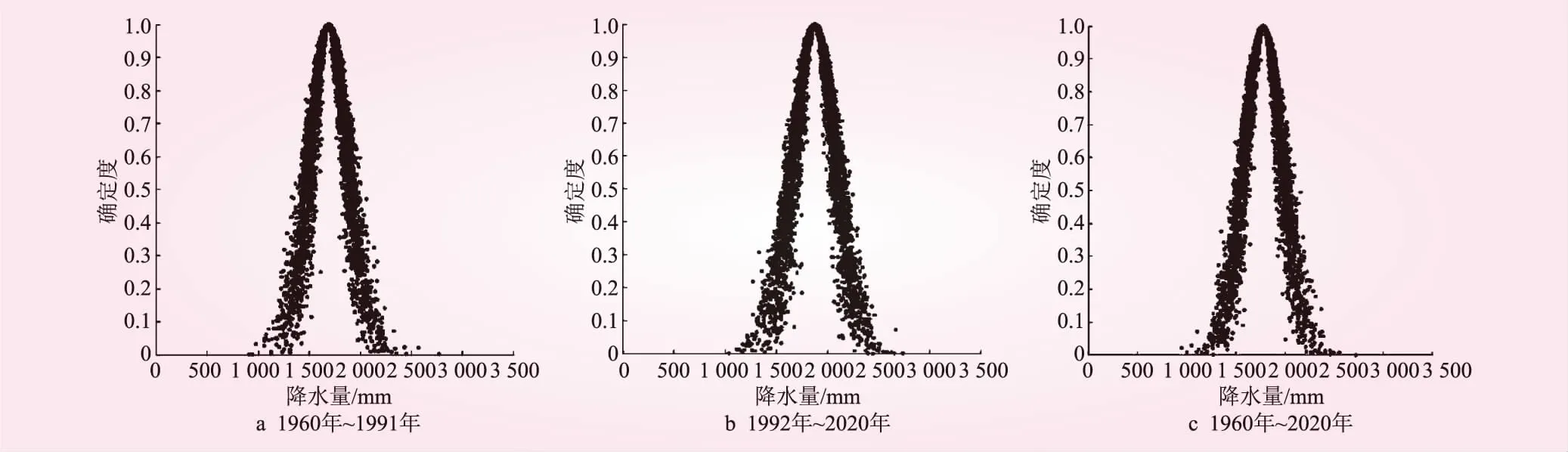
图10 不同时段年平均降水量空间分布隶属云图

由表2及图10可知，根据年降水空间分布在不同时段的比较，1992年～2020年与1960年～1991年相比，多年平均降水量增加了186 mm；熵值增大，说明降水更为离散；1992年～2020年隶属云图中云的厚度增大，即超熵增大，说明不稳定性增加，突变后的水资源管理难度更大。

结合表1可知，深圳市61 a的降水序列在时间分布上的熵值为317.1，大于空间分布上的熵值193.7；时间分布上的超熵值为77.9，大于空间分布的超熵值35.8。由此说明，深圳市的降水在时间分布上比空间分布更为离散，更不稳定，这主要是由于不同年份的降水量差异较大引起，而站点间的差异较小。

4 讨论

本研究表明，深圳市降水量的年际变化总体上呈增加趋势，这一结果与相关研究[2-3]结论基本一致。汛期降水占全年降水的85%左右，但是降水量往往集中在几场较大的降雨中，季节分配不均匀的高强度降水，容易导致洪涝灾害的发生。深圳市降水空间分布主要受地形影响，东部山地丘陵多，比西部地区更有利于水汽聚集，容易产生对流，雨量较为充沛，这与粤港澳大湾区年均降水量在空间上的分布类似[22]。

与前人研究相比，本文利用云模型从时间尺度和空间尺度分析了深圳市降水的分布特征，并且对其分布的离散程度及稳定性进行了量化，同时也是对前人研究深圳市降水分布的拓展及延伸。在云模型算法方面，采用了更完善的多步还原逆向云变换算法，基本保证超熵不会出现虚数的情形，使计算结果更为稳定。

深圳市降水在时间上的分布比空间分布上更不稳定，从近几年的实测降雨资料分析，时有突发干旱现象。因此，在做好防汛的同时，应进一步考虑雨洪资源的调蓄与利用，提高旱涝灾害的预警能力，增强城市发展韧性，促进经济社会可持续发展。

此外，区域降水的影响因素较多，随着全球气候变暖，极端天气频发，城市化的高度发展，深圳市及粤港澳大湾区的未来降水可能会产生新的变化特征，在未来降水预测方面有待进一步研究。