承压型组合剪力键剪切性能试验与承载力计算
2023-11-22马亚飞张建仁
马亚飞,周 彪,王 磊,张建仁
(长沙理工大学土木工程学院,湖南,长沙 410114)
钢-混组合梁是由钢主梁和混凝土桥面板组成的一种新型结构,能充分发挥钢材和混凝土的力学性能[1]。剪力键是保证钢主梁和混凝土桥面板协同受力的关键构件,主要分为焊钉和PBL(开孔钢板)剪力键,在实际工程中应用广泛。当组合梁的抗剪和抗拔需求较大时,对剪力键承载性能要求更高[2]。通过将焊钉和PBL 剪力键改进为一种肋板焊接横向焊钉的新型剪力键(简称组合剪力键),可进一步提高剪力键抗剪承载力,且避免发生高强T 型剪力键的脆性破坏[3]。因此,有必要对这种组合剪力键的抗剪机理展开研究。
国内外学者已对PBL 和焊钉剪力键极限承载力影响因素、计算模型和失效过程开展了试验研究和理论分析[4-6]。SHI 等[7]发现混凝土强度、钢筋直径和开孔数量对PBL 剪力键剪切性能影响显著,开孔孔径影响较小。WANG 等[8]开展了内嵌超高性能混凝土大直径焊钉剪力键推出试验,指出焊钉直径对剪力键抗剪性能有显著影响。赵晨等[9]提出了推出荷载下PBL 剪力键承载力计算表达式。杨勇等[10]基于变形协调条件构建了适应于单排多孔PBL 剪力键的极限承载力模型。陈海等[11]发展了斜板PBL 剪力键极限承载力计算方法。LOWE等[12]通过试验得到了横向荷载下焊钉剪力键的极限承载力,揭示了焊钉周围混凝土应力场的分布规律。DING 等[13]通过对混凝土强度、焊钉屈服强度和长径比等参数进行分析,研究了含焊钉剪力键组合梁的抗震性能。大跨度组合梁多采用宽幅悬臂梁设计。混凝土自重和移动荷载作用下会产生侧压效应[14-15]。宋瑞年等[16]建立了PBL 剪力键极限承载力增量与侧压力的关系。ZHAN 等[17]分析了侧压力对剪力键破坏形态的影响,并基于约束混凝土强度理论修订了PBL 剪力键极限承载力模型。静载下剪力键荷载-滑移曲线是反映其延性和刚度的重要指标[18]。GU 等[19]通过数值仿真开展了PBL 剪力键受力过程分析。杨勇等[20]等通过推出试验,发展了基于弹性地基梁理论的多孔PBL 剪力键荷载-滑移曲线模型。GUEZOULI 等[21]引入摩擦接触单元,建立了栓钉连接件二维有限元模型,量化了摩擦对剪力键荷载-滑移曲线的影响。现有研究主要围绕单调推出荷载下焊钉或PBL剪力键的极限承载力和失效过程开展研究。组合剪力键包含柔性焊钉和刚性开孔钢板[22],陈海等[23]采用叠加法,建立了非承压型组合剪力键的承载力计算表达式。承压型组合剪力键比非承压型组合剪力键增加了肋板端部承压效应,进一步优化了剪切荷载的纵向分布,其剪切机理和破坏模式尚未明确,亟待建立其承载力计算模型。
本文开展了11 个组合剪力键推出试验,对比了承压型和非承压型组合剪力键抗剪性能的差异,探讨了混凝土强度、肋板厚度、肋板孔径和焊钉直径对承压型组合剪力键极限承载力的影响;建立了承压型组合剪力键有限元计算模型,揭示了承压型组合剪力键受剪机理,提出了承压型组合剪力键极限承载力计算方法,并结合试验进行了验证。本研究可为组合剪力键极限承载力评估提供科学依据。
1 剪切性能试验
1.1 试件设计
试件设计依据钢-混组合结构欧洲规范4(EC4)[24],标准推出试件尺寸设计如图1 所示。组合剪力键由H 型钢、开孔肋板、焊钉和混凝土板组成。混凝土内部钢筋笼对称分布在剪力键两侧。组合剪力键分为承压型和非承压型,后者在肋板底部布置与肋板截面积相同的泡沫板,以消除肋板端部承压效应。非承压型剪力键混凝土桥面板需现浇,承压型剪力键可通过剪力槽孔与预制桥面板连接[2]。

图1 推出试件设计 /mmFig.1 Layout of push-out specimens
为研究两种组合剪力键在抗剪性能方面的差异,对11 个组合剪力键进行单调推出试验。试件编号规则为:混凝土强度-肋板开孔孔径-焊钉直径-肋板厚度。如C30-50-19-12 表示组合剪力键采用C30 混凝土,肋板孔径为50 mm,焊钉直径为19 mm,肋板厚度为12 mm,具体如表1 所示。
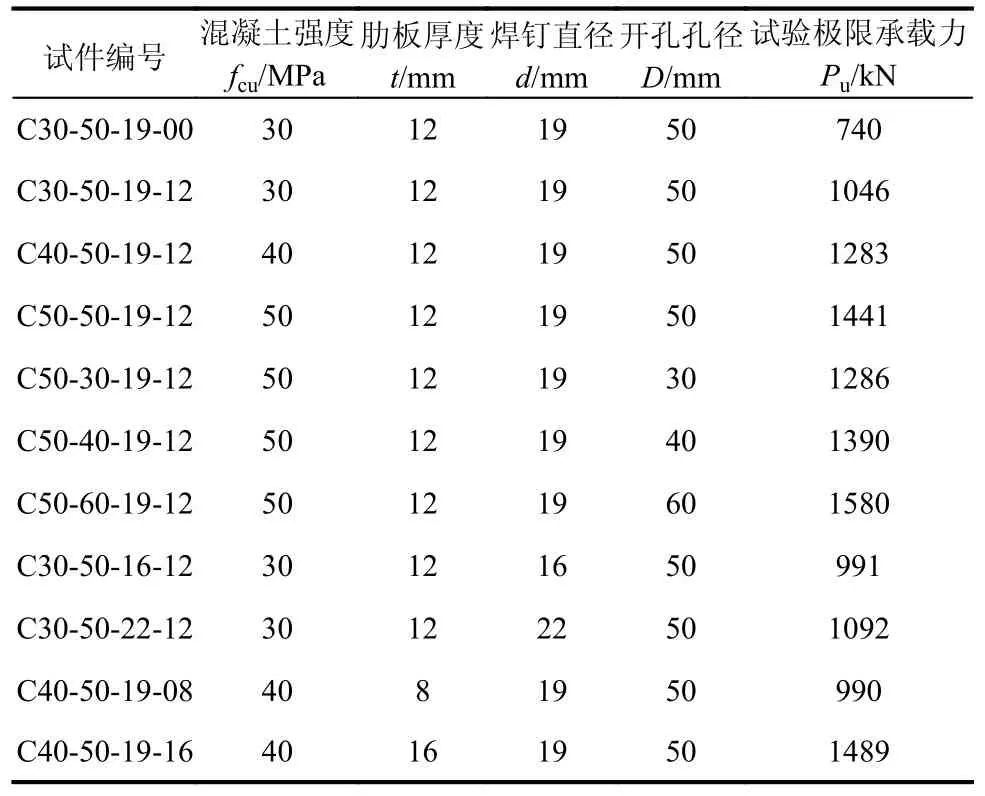
表1 试件设计参数Table 1 Parameter design of specimens
1.2 试验装置和加载过程
试验在500 t 长柱压力试验机上进行,如图2所示。为使试件两侧受力均匀,在H 型钢上表面放置橡胶垫。正式加载前先进行预加载,预压荷载为预估极限荷载(Pu)的30%。加载方式为单调分级加载,每级荷载持续10 min。试验前期采用力控制加载,每级荷载为0.1Pu,加载速率为0.5 kN/s,加载至0.4Pu后转为位移控制加载,每级位移量为1 mm,加载速率为0.03 mm/s,直至结构破坏。试验中主要测量压力机剪切荷载及H 型钢与混凝土板的相对滑移。荷载通过压力机读取,相对滑移通过对称布置在试件侧面的4 个百分表测量。

图2 加载装置Fig.2 Load setup
2 试验结果与分析
2.1 破坏形态
图3 和图4 为组合剪力键中混凝土板的破坏形态。由图3 可知,对于承压型组合剪力键,混凝土板外表面出现大面积劈裂裂缝,且主要集中在肋板下端面,混凝土内侧面也出现由焊钉高度附近向下发展的斜裂缝,劈裂裂缝相互贯通导致组合剪力键丧失承载力。

图3 承压型组合剪力键混凝土板破坏形态Fig.3 Failure mode of concrete slab of compressive composite shear connector

图4 非承压型组合剪力键混凝土板破坏形态Fig.4 Failure mode of concrete slab of non-compressive composite shear connector
由图4 可知,非承压型组合剪力键的破坏形态与承压型相比存在明显差异,由于无端部承压影响,组合剪力键主要依靠焊钉及混凝土榫抗剪承受外荷载,肋板下端面无大面积劈裂裂纹。组合剪力键内表面因焊钉承压,混凝土板出现劈裂主裂纹,导致组合剪力键失效。
图5 为组合剪力键内部破坏形态。无论是否考虑端部承压,除焊钉根部发生屈服或被剪断外,其余钢构件均无明显塑性变形。加载后期由于钢构件与混凝土板之间发生较大滑移,混凝土板中普通钢筋承担部分荷载,出现了较大弯曲变形。

图5 组合剪力键内部破坏形态Fig.5 Internal failure modes of combined connectors
2.2 试验结果分析
本部分先讨论肋板端部承压对组合剪力键极限承载力和破坏过程的影响,然后分析混凝土强度、肋板厚度、焊钉直径和肋板孔径等参数影响下的承压型组合剪力键受力性能。
2.2.1 端部混凝土承压影响
端部承压效应影响下组合剪力键的荷载-滑移曲线如图6 所示。由图6 和表1 可知,承压型组合剪力键C30-15-19-12 的极限承载力为1046 kN,非承压型组合剪力键C30-50-19-00 的极限承载力为740 kN,降幅为29.3%。由于承压型组合剪力键的肋板端部混凝土有承压作用,可有效抑制混凝土与剪力键间的相对滑移,极限承载力显著提高。
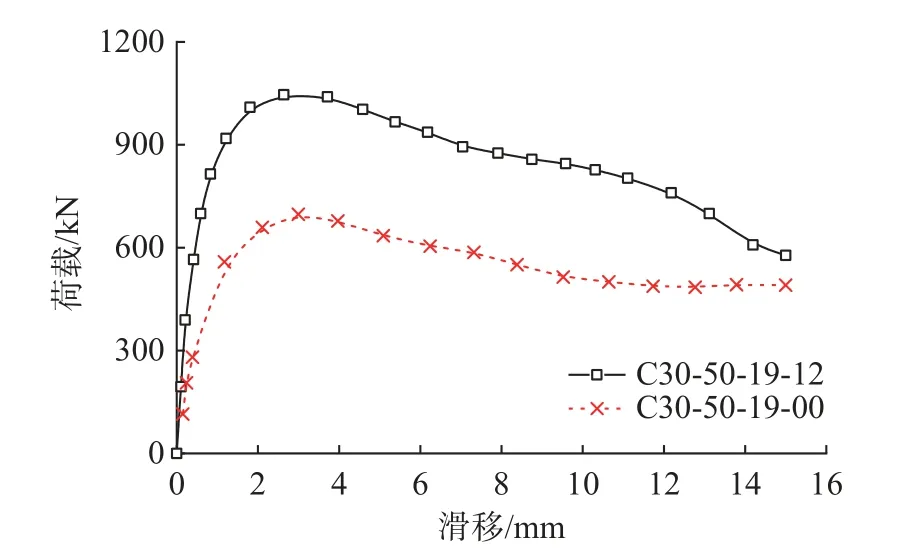
图6 端部承压影响Fig.6 Influence of end pressure
2.2.2 混凝土强度影响
混凝土强度对承压型组合剪力键极限承载力的影响如图7 所示。由图7 可知,模型C30-50-19-12 的极限承载力为1046 kN,模型C50-50-19-12的极限承载力为1441N,承载力增大37.8%。这表明混凝土强度对承压型组合剪力键的极限承载力影响显著,在进行大跨径钢-混组合梁设计时,可通过提高混凝土强度来增强混凝土桥面板与钢主梁间的抗剪性能。
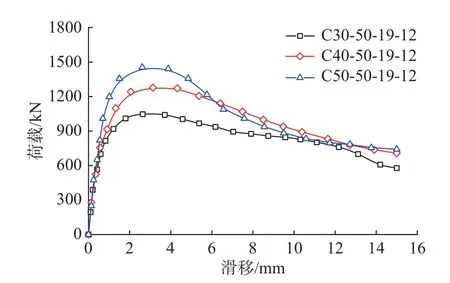
图7 混凝土强度影响Fig.7 Influence of concrete strength
2.2.3 肋板厚度影响
由表1 可知,肋板厚度由8 mm 增长至16 mm,组合剪力键的极限承载力提高34.2%。肋板厚度对承压型组合剪力键极限承载力的影响如图8 所示。由图8 可知,增加肋板厚度会显著提高承压型组合剪力键的极限承载力,进入破坏阶段后,薄肋板组合剪力键承载力下降速率显著降低,即薄肋板组合剪力键延性更高,峰值荷载下滑移由5.28 mm 减小至2.57 mm,降幅51.4%。这主要是因为随肋板厚度的降低,肋板刚度下降,破坏时肋板下端面发生明显塑性变形,同时因端部混凝土承压作用削弱,混凝土板劈裂效应显著降低,减缓了剪力键与混凝土板间的相互分离,剪力键与混凝土板仍可协同承受较大荷载。因此,对延性有较高要求的大跨径钢-混组合梁,可通过增加组合剪力键数量同时降低肋板厚度,以满足对组合剪力键的承载力和延性要求。
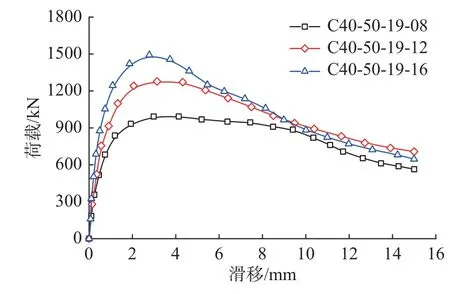
图8 肋板厚度影响Fig.8 Influence of rib plate thickness
2.2.4 肋板孔径影响
对于承压型组合剪力键,开孔肋板中未设置贯穿钢筋,孔内混凝土未受到有效约束,混凝土榫(肋板孔内混凝土)受剪以承受外荷载。肋板孔径对组合剪力键破坏过程的影响如图9 所示。由图9 和表1 可知,肋板孔径以10 mm 为增量,由30 mm 增至60 mm,极限承载力分别增长8.1%、12.1%和22.8%,相比混凝土强度、肋板厚度等参数,承压型组合剪力键极限承载力对开孔孔径的敏感性较低。进入破坏阶段后,由于混凝土榫快速被剪断,剪力键由端部承压和焊钉剪切作用承受外荷载,荷载-滑移曲线较接近。因此,改变肋板孔径对组合剪力键力学性能影响较小。
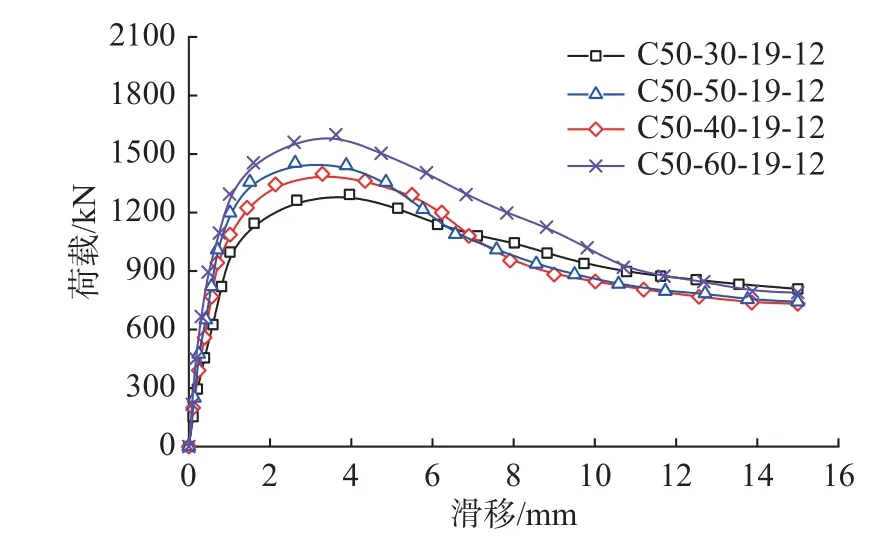
图9 肋板孔径影响Fig.9 Influence of rib plate aperture
2.2.5 焊钉直径影响
焊钉直径对承压型组合剪力键极限承载力的影响如图10 所示。由图10 可知,组合剪力键极限承载力随焊钉直径的增加而增加。由表1 可知,焊钉直径由16 mm 增加至19 mm,极限承载力提高12.2%;直径由19 mm 增至22 mm,极限承载力增加7.9%,极限承载力增幅呈下降趋势。主要原因为大直径焊钉刚度远大于焊钉周围混凝土,焊钉发生较小塑性变形,焊钉内侧混凝土板形成斜向主裂缝,焊钉与混凝土板分离,焊钉机械阻力失效,焊钉刚度无法充分利用。因此,针对采用普通混凝土板的钢-混组合梁,建议组合剪力键焊钉直径不宜超过19 mm。
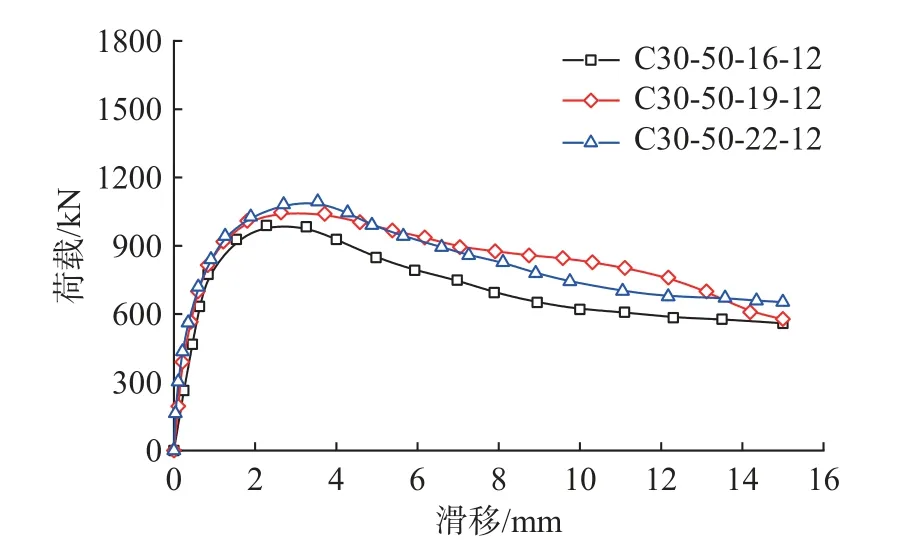
图10 焊钉直径影响Fig.10 Influence of stud diameter
3 有限元模型与验证
为进一步探究承压型组合剪力键破坏机理,并为参数分析提供数据支撑,结合剪力键对称性,建立了1/4 推出试件的有限元模型,如图11 所示。
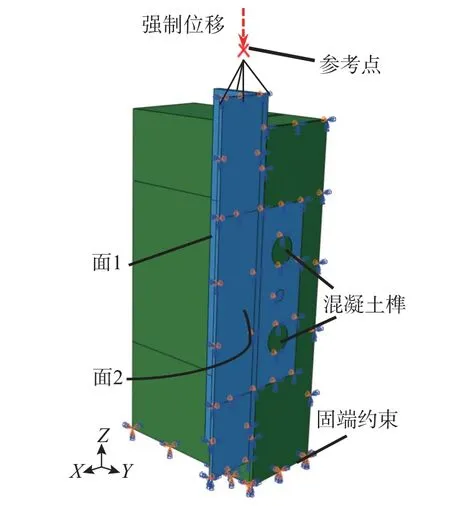
图11 有限元模型Fig.11 Finite element model
3.1 本构模型
混凝土采用塑性损伤模型,混凝土本构关系由式(1)和式(2)控制:
式中:σc(σt)为混凝土压(拉)应力;εc为混凝土压应变;Ec为混凝土弹性模量;η 为混凝土压应变与峰值应变之比,η=εc/εcp,εcp=0.0025;w为裂缝宽度;wc为应力完全释放时的裂缝宽度;k为塑性值,k=Ec×εcp/fc;fc为混凝土圆柱体抗压强度;ft为混凝土抗拉强度;常数项c1=3,c2=6.93。不同混凝土材料参数取值见表2。
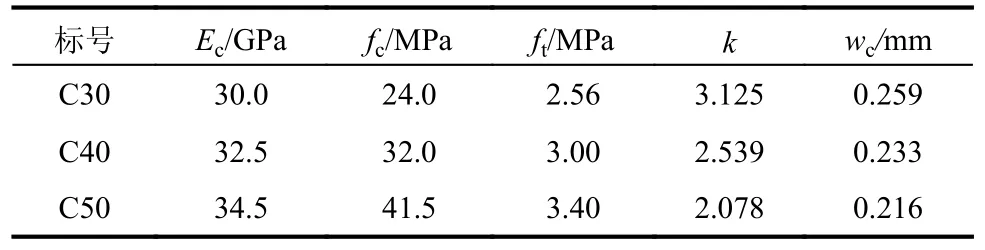
表2 混凝土材料参数取值表Table 2 Value table of concrete material parameters
混凝土受压损伤dc、受拉损伤dt分别与塑性应变和塑性裂缝宽度wpl相关,混凝土塑性损伤因子可表示为:
式中:常数项bc=0.7;bt=0.1。
钢筋采用HPB235 光圆钢筋,肋板和H 型钢采用Q345 钢,其应力-应变曲线采用三折线模型,如图12 所示。
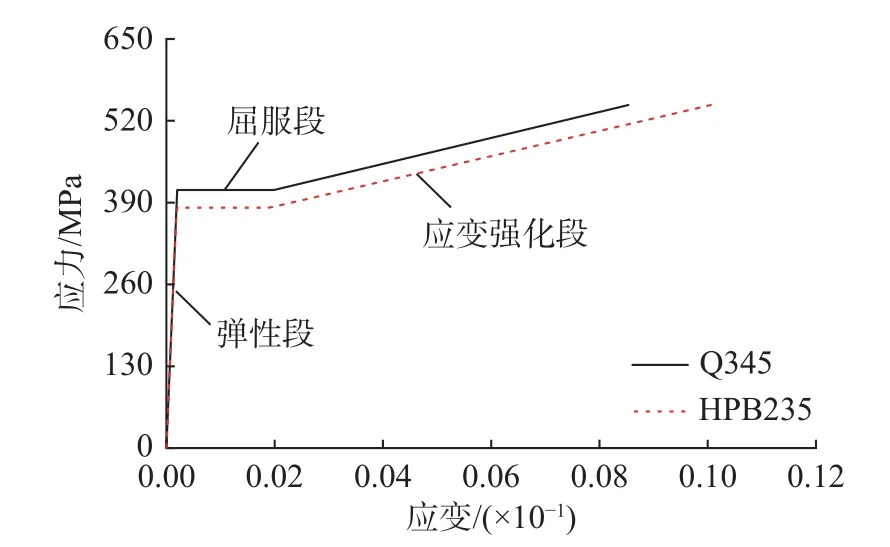
图12 钢材本构模型Fig.12 Constitutive model of steel
3.2 边界设置与网格划分
按位移控制模式加载,位移幅值为15 mm。加载时,对H 型钢上端参考点施加竖直向下的强制位移。对面1 和面2 施加对称边界条件,在混凝土板底部施加固端约束,如图11 所示。忽略剪力键与混凝土间的切向摩擦作用,法向设置为“硬”接触。通过动力显式分析法对有限元模型进行求解。
剪力键和混凝土板采用三维八节点减缩积分单元(C3D8R),钢筋采用三维桁架单元(T3D2)。网络全局种子设置为15 mm~20 mm,在剪力键与混凝土板接触区域进行局部网格加密,网络划分如图13 所示。
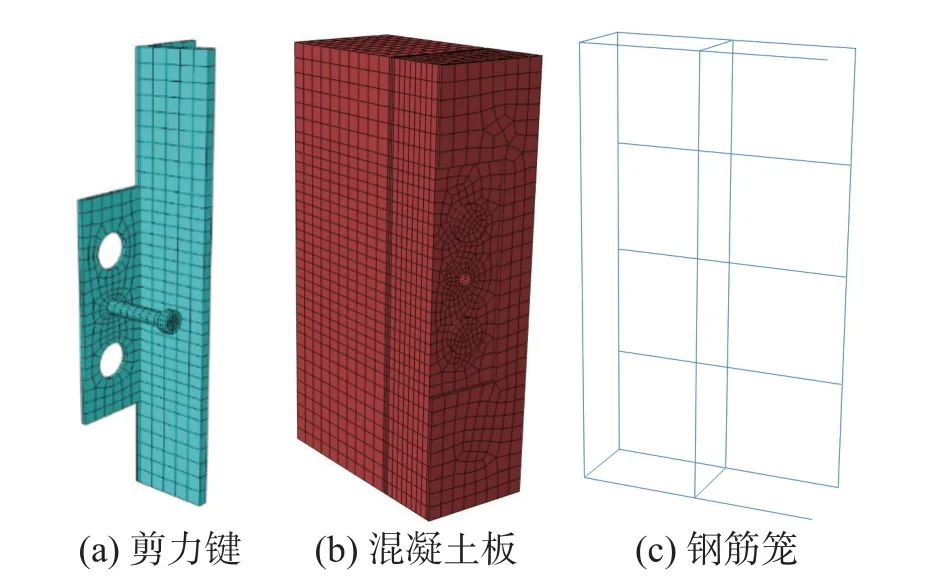
图13 不同构件网格划分Fig.13 Meshing of different components
3.3 有限元模型验证
有限元分析与试验得到的组合剪力键失效模式如图14 所示。根据试验和数值分析结果,初始裂纹出现在肋板承压端并逐步延伸,形成竖向裂缝和端部劈裂裂缝。破坏阶段,混凝土板内表面横向斜主裂缝延伸至外表面,混凝土板端部局部被压碎。剪力键焊钉根部屈服,其余部位保持完好。
为进一步验证有限元模型的可靠性,对有限元分析结果和实测荷载-滑移曲线进行比较,如图15所示。图15 中:FC 为计算值;C 为试验值。由图15可知,理论值与试验值较为吻合,表明本研究提出的有限元建模方法能有效模拟组合剪力键的破坏全过程。

图15 荷载-滑移曲线对比Fig.15 Load-slip curve comparison
4 组合剪力键承载力计算
4.1 组合剪力键受剪机理
图16 给出了承压型组合剪力键的剪切机理分析模型。图16 中:P为竖向荷载;Vp1为端部承压作用;Vp2为混凝土销栓作用;Vs为焊钉机械阻力。竖向荷载P可表示为:
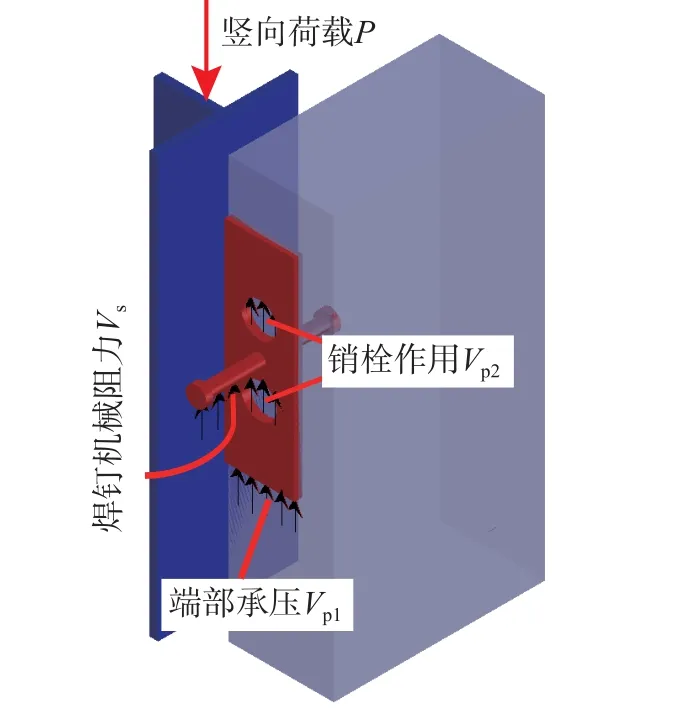
图16 组合剪力键剪切机理分析模型Fig.16 Shear mechanism analysis model of combined connector
以模型C30-50-19-12 为例,对组合剪力键受力过程进行分析,如图17 所示,Pp为开孔钢板承受荷载(Pp=Vp1+Vp2),Vs为焊钉承受荷载。由图17可知,在弹性阶段,开孔钢板和焊钉承受荷载均随滑移量的增加而增加;进入破坏阶段,混凝土板产生劈裂破坏,剪力键与混凝土板相互分离,Pp和Vs均下降,二者变化趋势相近。
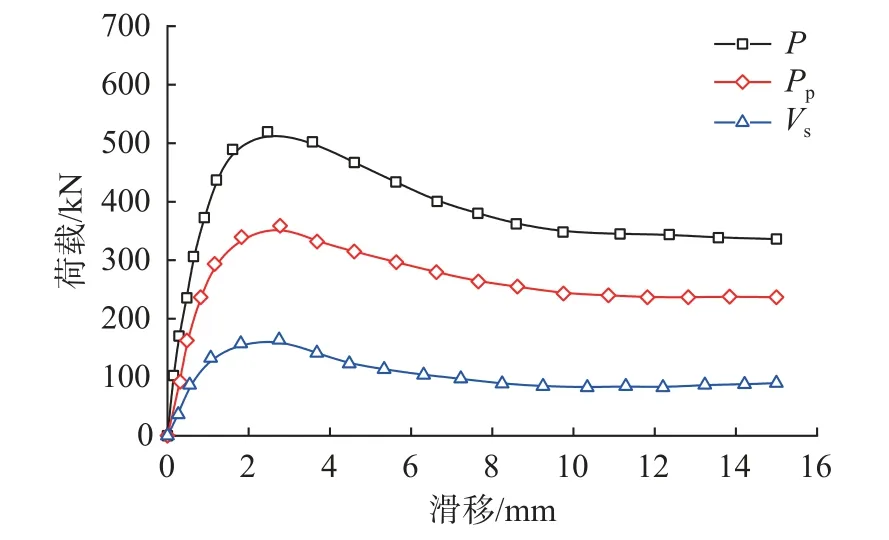
图17 组合剪力键受力过程分析Fig.17 Analysis on loading process of combined connector
4.2 有限元参数设置
为进一步探究混凝土强度、肋板厚度、肋板孔径和焊钉直径对承压型组合剪力键极限承载力的影响,采用正交试验设计法[25],建立并分析了108 组承压型组合剪力键有限元模型,具体参数设置如表3 所示,有限元分析结果如图18 所示。

表3 推出试件参数设计Table 3 Parameter design of push-out specimens

图18 有限元参数分析结果Fig.18 Results of FEM parametric analysis
由图18 可知,承压型组合剪力键极限承载力分别与混凝土强度的平方根和肋板厚度近似呈线性关系,与肋板孔径和焊钉直径的平方近似呈正比。值得注意的是,C50-60-19-8 的极限承载力比C50-50-19-8 降低了6.1%。主要原因为薄肋板损伤较大,混凝土因强度较高尚未破坏。因此,采用高强度混凝土设计钢-混组合梁时,应避免使用薄肋板且大孔径构造的承压型组合剪力键。
4.3 组合剪力键极限承载力模型
基于既有公式[26-28]与图18 中的线性关系及量纲平衡,可分别建立端部混凝土承压、混凝土榫抗剪及焊钉机械阻力对承压型组合剪力键极限承载力的影响模型:
式中:p1、p2、p3为待定系数;h为剪力键高度;Asc为孔内混凝土面积,Asc=πD2;Ec为混凝土弹性模量。
为确定式(6)~式(8)中待定系数p1、p2和p3,随机选取72 组承压型组合剪力键极限承载力数值分析结果进行多变量线性回归分析,式(5)可进一步写为:
图19 为计算值与试验值和有限元分析结果的对比,并给出了理想预测值和95%置信区间。由图19 可知,理论计算值与有限元和试验结果吻合较好。90%以上有限元计算值落在置信区间(CI)内,理论计算与有限元分析结果比值的均值为0.953,标准差为0.078,表明该理论模型在数值仿真中得到了验证。此外,试验点均落在置信区间内,理论计算与试验结果比值的均值为0.987,标准差为0.045,进一步验证承压型组合剪力键极限承载力计算模型的准确性。
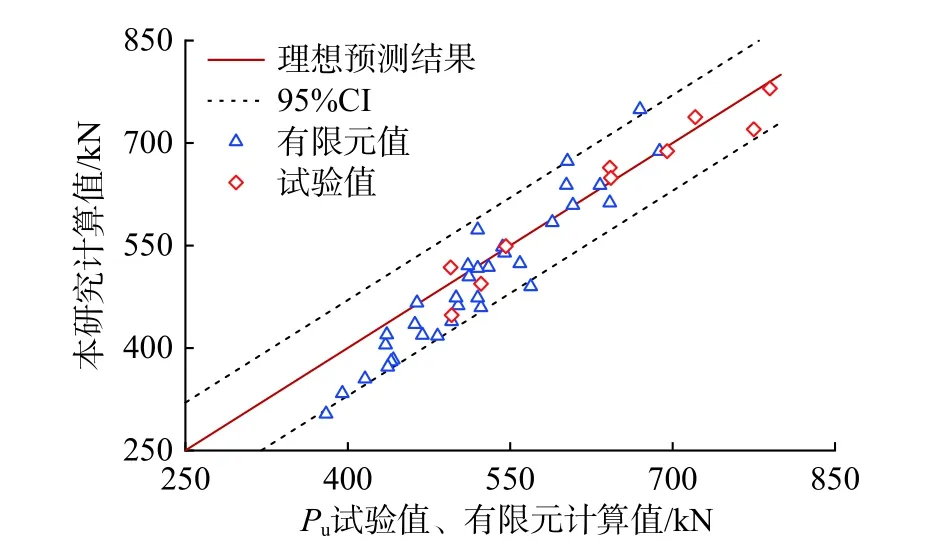
图19 极限承载力对比Fig.19 Comparison of ultimate carrying capacity
5 结论
本文针对抗剪要求较大的钢-混组合梁,改进了一种承压型组合剪力键,对其抗剪性能进行研究得出如下结论:
(1) 对比了非承压型与承压型组合剪力键的抗剪承载能力,C30-50-19-12 的极限承载力约为C30-50-19-00 的1.4 倍。
(2) 进入破坏阶段,承压型组合剪力键混凝土板中心线与肋板下端面出现大面积竖向裂缝和端部裂缝,内侧面形成由焊钉高度附近向下延伸的斜主裂缝,非承压型组合剪力键混凝板无明显端部裂缝。
(3) 焊钉直径和肋板孔径对承压型组合剪力键极限承载力影响较小,混凝土强度和肋板厚度对承压型组合剪力键极限承载力影响显著。混凝土强度从C30 增至C50 时,承压型组合剪力键极限承载力提高37.8%,肋板厚度从8 mm 增至16 mm时,极限承载力提高34.2%。
(4) 基于承压型组合剪力键试验和108 个数值模型分析结果,利用多元线性回归法,提出了承压型组合剪力键极限承载力计算公式,该式物理意义明确,计算值与仿真和试验结果相吻合。
由于样本数量有限,提出的计算模型有待进一步验证。另外,本研究未考虑腐蚀环境对组合剪力键破坏机理的影响,仍需日后进一步研究。
