气-膜耦合作用对充气薄膜管动力特性的影响

王晓峰，付慧杰，杨庆山

(1.北京交通大学土木建筑工程学院，北京 100044；2.重庆大学土木工程学院，重庆 400044)

充气膜因质量轻、折叠体积小、成型快等优点，广泛应用于土木工程的大跨建筑结构和航空航天领域的空间可展结构。充气膜属于柔性结构，通过内充气压使外围薄膜产生预张力而获得刚度，在荷载作用下易产生较大的变形，从而引起内充气体体积和压力的显著改变。而内充气压的变化又影响外围薄膜的张拉应力，进而影响充气膜的刚度和变形。这种内充气体压力与外围薄膜变形之间的耦合作用(气-膜耦合作用)对充气膜的力学行为产生重要影响。充气薄膜管属于气肋式充气膜，多用于薄膜结构的支撑构件，其动力特性必然对整个薄膜结构的动力行为产生重要影响。研究气-膜耦合作用对充气薄膜管动力特性的影响，有助于准确认识其动力性能，保证薄膜结构设计、计算的合理性和工程应用的可靠性。

现有文献多关注充气膜的静力性能，在形态分析[1-5]、充气阶段的平衡构形[6-9]、外围薄膜的力学性能[10-16]、接触力学问题[17-21]以及褶皱变形的影响[22-29]等方面进行了研究。关于充气膜动力性能的研究则相对较少，对于充气薄膜管，仅涉及自振特性分析[30-33]和充气展开过程中的动力性能分析[34-37]这两个方面。

而目前充气膜力学性能的研究，通常将内充气压等效为外围薄膜的静力边界条件，或者假定内充气体满足理想气态方程[38-39]，而考虑气-膜耦合作用影响的研究文献很少。文献[40]通过将外围流场离散为三维声学流体单元对充气薄膜梁进行湿模态分析，通过与相应的干模态分析结果进行对比，研究了外部流场对充气薄膜梁动力特性的影响。文献[41 - 42]假定内充气体为非定常、可压缩的理想气体，研究了充气薄膜管展开过程中气-固耦合作用的影响。

本文基于作者对气-膜耦合作用的静力研究成果[43-44]，对充气薄膜管的动力特性进行有限元分析，研究气-膜耦合作用对自振特性的影响规律。考虑到充气薄膜管外围薄膜质量轻，内充气体的附加质量在总质量中占有较大的比重，也对其影响作用进行探究。通过将内充气体看作小扰动线性势流以考虑气-膜耦合作用和内充气体附加质量的影响。借助商用有限元软件ADINA，建立内充气体的三种等效模型，分别将内充气体作用等效为外围薄膜静力边界条件(模型M1)，同时考虑内充气体附加质量影响的静力边界条件(模型M2)以及小扰动线性势流体(模型M3)，通过将其相应的有限元分析结果进行对比，研究气-膜耦合作用和内充气体附加质量对充气薄膜管动力特性的影响及其随初始内压、长细比、膜厚和端部约束类型等因素的变化规律。

1 理论基础

外围薄膜和内充气体的物理特性及其相互耦合作用决定了充气薄膜管的力学行为，因此，可通过外围薄膜和内充气体的力学微分方程以及气-膜耦合作用方程建立充气薄膜管的控制方程。

1.1 薄膜微分方程

假定薄膜的变形具有大转动、小应变特点，而且在整个变形中保持为线弹性本构关系，即应力-应变关系满足广义胡克定律。同时，假定薄膜具有微小的抗弯刚度，其褶皱变形实际上是薄壳在压应力作用下的局部屈曲，可基于式(1)给出的板壳稳定方程[45]通过非线性屈曲分析求得。

式中： Σ=σh，σ 为二维Cauchy 应力张量，h为薄膜厚度；为薄膜单位面积质量；x为二维位置矢量；x¨=∂2x/∂t2；x˙=∂x/∂t，t为时间；μ为单位面积阻尼系数；w为薄膜中面的挠度；w¨=∂2w/∂t2；，E为弹性模量，ν为泊松比；L为微分算子，且L=∇⊗∇ ； ∇=∂/∂x为梯度算子；q为垂直于膜面的外荷载。式(1)为基于Föppl-von Kármán 理论的板壳稳定方程。对该方程的位移场进行有限元离散，由变分原理可得离散后的薄膜动力方程为：

式中：MS和CS分别为薄膜的质量矩阵和阻尼矩阵；u¨=∂2u/∂t2；u˙=∂u/∂t；u为薄膜单元的结点位移向量；fin(u)为薄膜单元的结点内力向量，是单元结点位移的函数；fex=Q+PS，Q和PS分别为外荷载和内充气压所对应的薄膜单元结点外力向量。

1.2 内充气体微分方程

充气薄膜管中的内充气体属于封闭流场，因外围薄膜变形而产生的扰动速度很小，可假定其为均匀、无旋、无粘的理想流体，且在变化过程中始终满足等熵条件。这样，内充气体可看作线性有势流体[46]，在小扰动条件下满足波动方程[47]：

式中： ∇2=∇·∇为拉普拉斯算子；c为音速；φ¨=∂2φ/∂t2； φ为速度势函数，即

式中，vF为内充气体速度矢量。式(3)为关于函数φ的线性微分方程，在其求解域内分片离散场函数φ，并通过Galerkin 法使加权余量为零，可得有限元离散格式的线性方程为[46]：

1.3 气-膜耦合作用方程

当不考虑内充气体的粘性时，充气薄膜管在内充气体和外围薄膜耦合界面处，有：

式中：vF,n和pF分别为内充气体在气-膜耦合界面处的法向速度以及承受的薄膜压力作用；vS,n和pS分别为外围薄膜在气-膜耦合界面处的法向速度以及承受的内充气体压力作用。由式(6)可以得到有限元离散后的耦合方程为[46]：

式中：T为薄膜位移投影到耦合界面法线方向的转换矩阵；；NS为薄膜单元的形函数矩阵。将式(7)的第一式和第二式分别代入式(5)和式(2)得：

式(8)和式(9)为考虑气-薄膜耦合作用的充气薄膜管有限元离散方程。当充气薄膜管的外荷载为零，且不考虑结构阻尼时，式(8)退化为：

式(9)和式(10)为考虑气-膜耦合作用的充气薄膜管自由振动方程。

2 有限元模型

根据式(9)和式(10)建立的考虑气-膜耦合作用的充气薄膜管自由振动方程，借助商用有限元软件ADINA 对充气薄膜管的动力特性进行有限元分析。根据1.1 节的基本假定，将外围薄膜看作Kirchhoff 材料，采用四结点壳单元进行有限元离散；根据1.2 节的基本假定，对内充气体采用八结点的线性势流单元进行离散，以考虑内充气体与外围薄膜的耦合作用。充气薄膜管两端采用与试验相同的金属盖板封闭，以便于与试验结果进行比较。两端金属盖板采用四结点壳单元进行离散。

图1 给出了充气薄膜管在膜厚h=0.075 mm、半径r=50 mm、长细比λ=7、两端固定、内压P0=4 kPa情况下(其他材料参数如表1 所示)，前5 阶自振频率随单元数量的变化情况。横坐标num 为薄膜单元数量，纵坐标Δf为不同单元数量得到的同阶频率差值，n为频率的阶次。从图1 可以看出，随着薄膜单元数量的增加，频率的差值逐渐减小，最终趋于零。

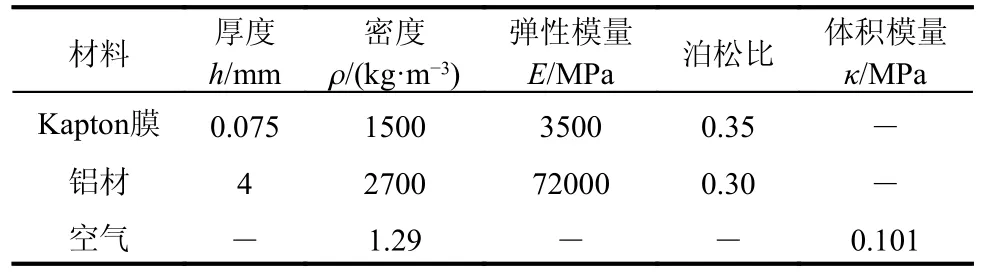
表1 充气薄膜管材料参数[44]Table 1 Material properties of the inflated membrane tube[44]

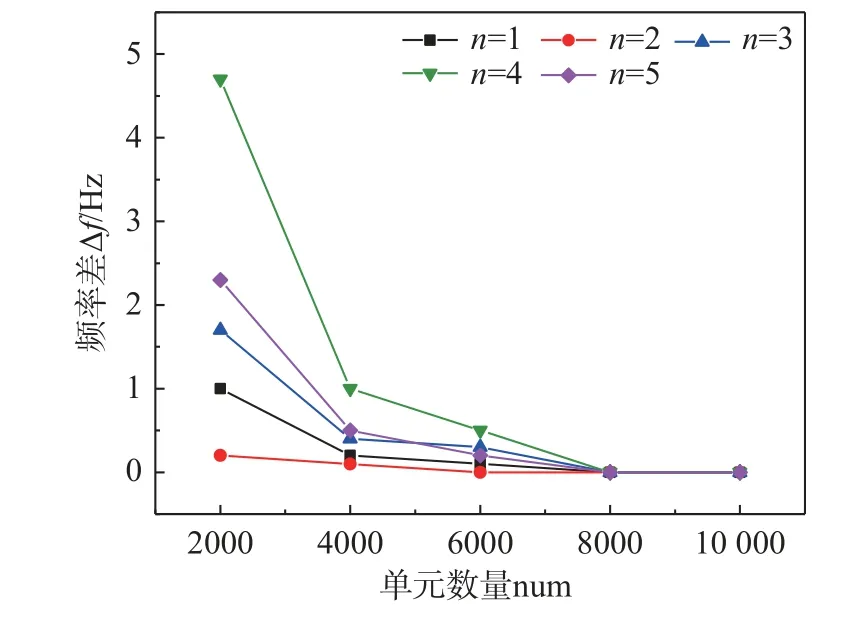
图1 前5 阶自振频率随单元数量变化情况[44]Fig.1 Variations of the first five-order natural frequencies with the element number[44]

根据图1 给出的充气薄膜管的前5 阶自振频率随单元数量的变化情况，权衡其计算精度和计算时间，最终确定外围薄膜的单元数量为8000 个，单元尺寸为3.93 mm×7.00 mm；内部势流的单元数量为84 400 个，单元尺寸为(2.91 mm～3.93 mm)×(2.91 mm～3.93 mm)×7.00 mm；两端盖板的单元数量为844 个，单元尺寸为(2.91 mm～3.93 mm)×(2.91 mm～3.93 mm)。建立的有限元模型如图2 所示。

图2 充气薄膜管有限元模型[44]Fig.2 Finite element model of the inflated membrane tube[44]

充气薄膜管外部薄膜采用Kapton 膜材，内充气体为空气，两端采用铝制盖板封闭，相应的材料参数如表1 所示。充气薄膜管的端部盖板刚度远大于外围薄膜，可将其看作刚性平面，通过约束其作为刚体的三个平动和三个转动自由度来实现固定约束条件；通过约束其作为刚体的三个平动自由度和绕z轴(纵轴)和y轴(弯曲平面内的横截面形心惯性轴)的转动自由度来实现简支约束条件。

具体有限元分析过程如下：

1) 通过对外围薄膜、端盖板采用四结点壳单元进行有限元离散，建立式(10)相应的结构离散模型。

2) 对内充气体采用八结点的线性势流单元进行有限元离散，建立式(9)相应的势流场离散模型。

3) 通过薄膜单元和势流单元在交界面上共享结点实现气-膜耦合，形成式(9)和式(10)中的耦合矩阵A。

4) 在充气薄膜管两端施加边界条件，然后对离散后的内充气体施加质量流荷载使其达到初始内压，同时使外围薄膜产生预张应力。

5) 对充气薄膜管进行模态分析，即通过Lanczos方法求解式(9)和式(10)确定的特征值问题，获得其自振频率和自振模态。

3 有限元模型验证

3.1 静力验证

通过研发试验装置，对充气薄膜管进行静力加载试验，验证本文建立的考虑气-膜耦合作用有限元模型在静力分析时的正确性和精确性。静力分析时的边界条件如图3 所示，研发的试验装置如图4 所示。试验中，通过砝码施加竖向和横向荷载；位移和内压分别采用松下HG-C1100 激光位移计和数字差压计进行量测；充气设备为220 V单缸充气泵，并在排气口位置处安装活塞用于气压微调，确保初始气压的精度。

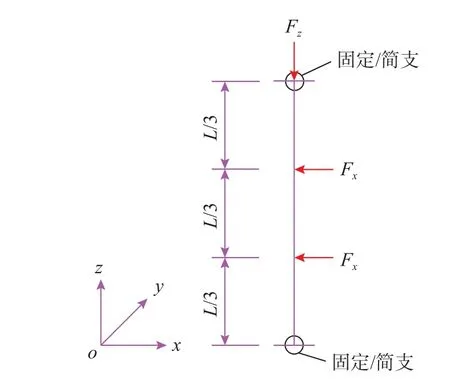
图3 充气薄膜管荷载作用示意图[44]Fig.3 Diagram of the inflated membrane tube under load[44]

图4 试验装置实物图[44]Fig.4 Experimental setup[44]

图5 给出了充气薄膜管在直径100 mm、长细比为7、膜厚75 µm 以及内充气压为6 kPa 情况下试验与数值的对比结果。有限元模型信息和物理参数如第2 节所示，考虑了气-膜耦合作用和内充气体附加质量的影响。静力有限元分析中，根据第1 阶特征值屈曲模态施加初始缺陷，考虑几何非线性的影响[44]。内充气体为恒质量情况下内压P、跨中横向位移uH随横向荷载FH的变化曲线如图5(a)、图5(b)所示。

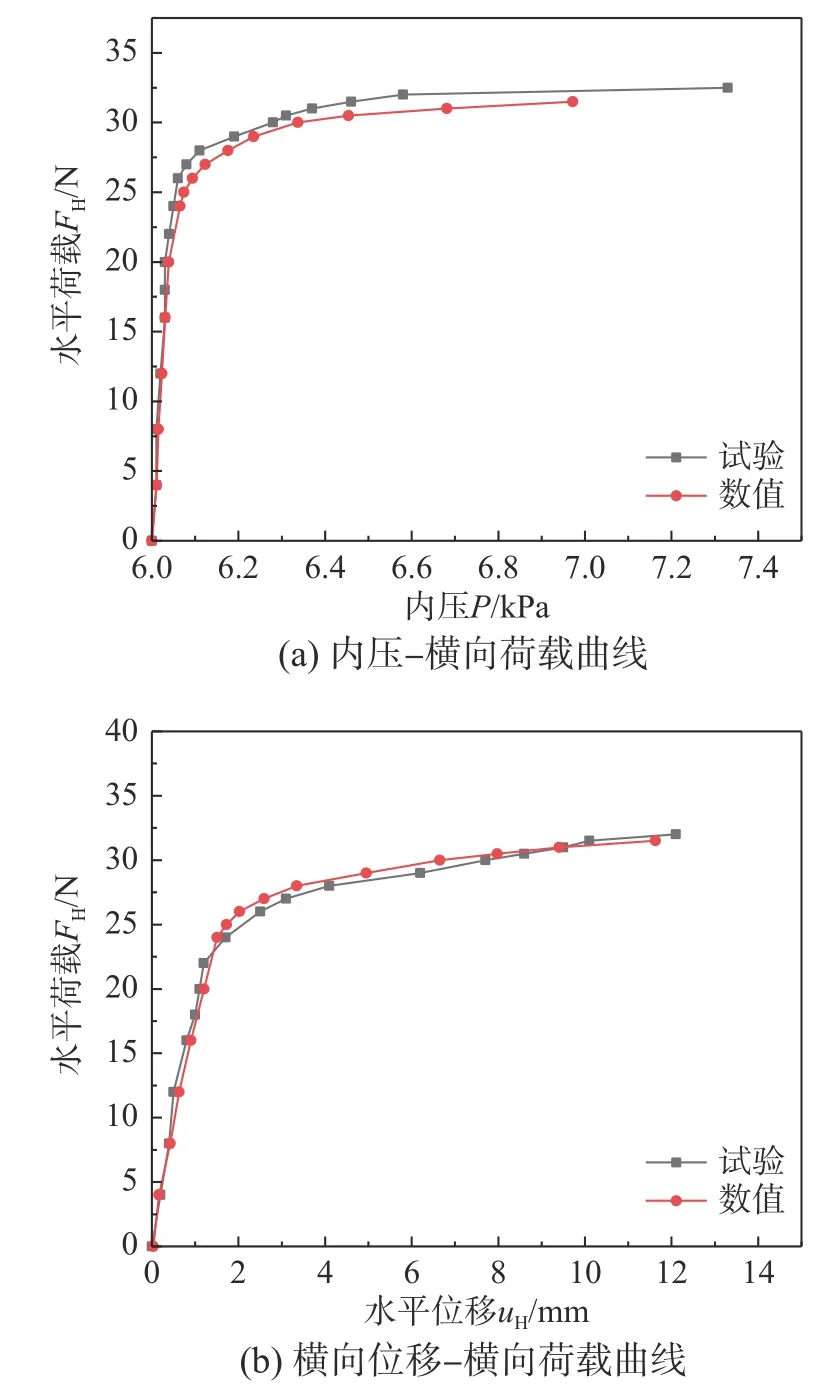
图5 试验和有限元分析结果对比Fig.5 Comparison between experimental and numerical results

从图5 的对比结果可以看出，分别由试验和有限元分析得到的内压-荷载曲线以及位移-荷载曲线均吻合很好，从而验证了本文建立的充气薄膜管有限元模型在考虑气-膜耦合作用和内充气体附加质量影响的情况下，静力分析的正确性和精确性。

3.2 动力特性验证

通过与文献[48]中相应的试验和数值计算结果进行对比，验证本文建立的考虑气-膜耦合作用的充气薄膜管有限元模型在模态分析中的有效性和精确性。文献[48]中充气薄膜管两端为固定约束，具体几何及物理参数取值如表2 所示。

表2 充气薄膜管参数[48]Table 2 Parameters of the inflated membrane tube[48]

表3 给出了分别由文献[48]试验和本文有限元分析得到的前3 阶自振模态形状。表4 给出了分别由文献[48]试验和有限元分析(将内充气体等效为外围薄膜的静力边界条件而未考虑气-膜耦合作用)得到的前3 阶自振频率以及相应的本文有限元分析(考虑气-膜耦合作用)结果。

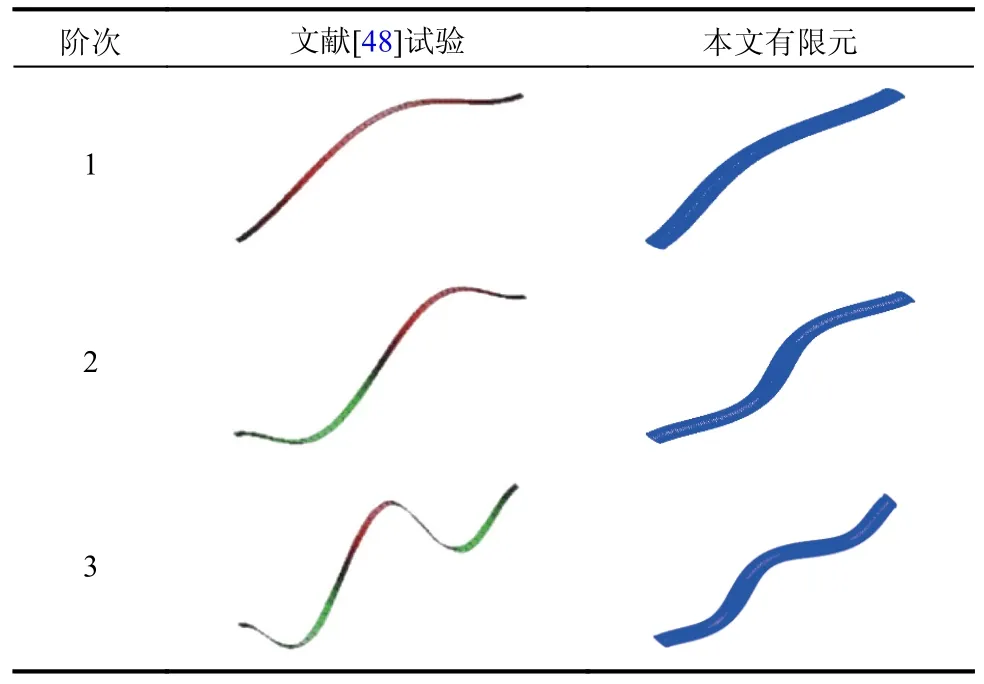
表3 充气薄膜管自振模态Table 3 Modal shapes of the inflated membrane tube

表4 充气薄膜管自振频率Table 4 Natural frequencies of the inflated membrane tube

由表3 和表4 可知，由本文有限元模型得到的前3 阶自振模态和相应频率与文献[48]试验结果吻合很好，频率最大误差为1.1%。而文献[48]在有限元分析中，由于没有考虑气-膜耦合作用以及内充气体附加质量的影响，其频率计算结果与试验结果差异较大。可见，将内充气体作用等效为外围薄膜的静力边界条件会导致较大的计算误差，应考虑气-膜耦合作用的影响。而本文建立的考虑气-膜耦合作用的充气薄膜管有限元模型具有良好的精度，可用于研究气-膜耦合作用对充气薄膜管动力特性的影响及其随参数的变化规律。

4 气-膜耦合作用对动力特性的影响

基于如表5 所示的三种内充气体等效模型(M1、M2、M3)，对充气薄膜管进行模态分析。通过将三种模型的计算结果进行对比，研究气-膜耦合作用对充气薄膜管动力特性的影响及其随初始内压、长细比、膜厚以及端部约束类型的变化规律，并探究内充气体附加质量的影响程度。各影响因素的取值范围以及相应的其他参数取值情况如表6所示。由于三种模型对模态形状没有明显影响，4.1 节～4.4 节只给出由模型M3(将内充气体等效为有势流体)得到的前5 阶模态形状。

表5 内充气体的等效模型Table 5 Equivalent models of the inner air

表6 影响因素及其他参数取值Table 6 Values of the influencing factors and other parameters

4.1 随初始内压的变化

对初始内压分别为2 kPa、4 kPa、6 kPa、8 kPa、10 kPa、12 kPa 情况下的充气薄膜管进行自振特性分析，研究气-膜耦合作用随初始内压的变化规律，其他参数及物理特性取值分别如表6 和表1 所示。表7 给出了模型M3 的前5 阶自振模态形状。

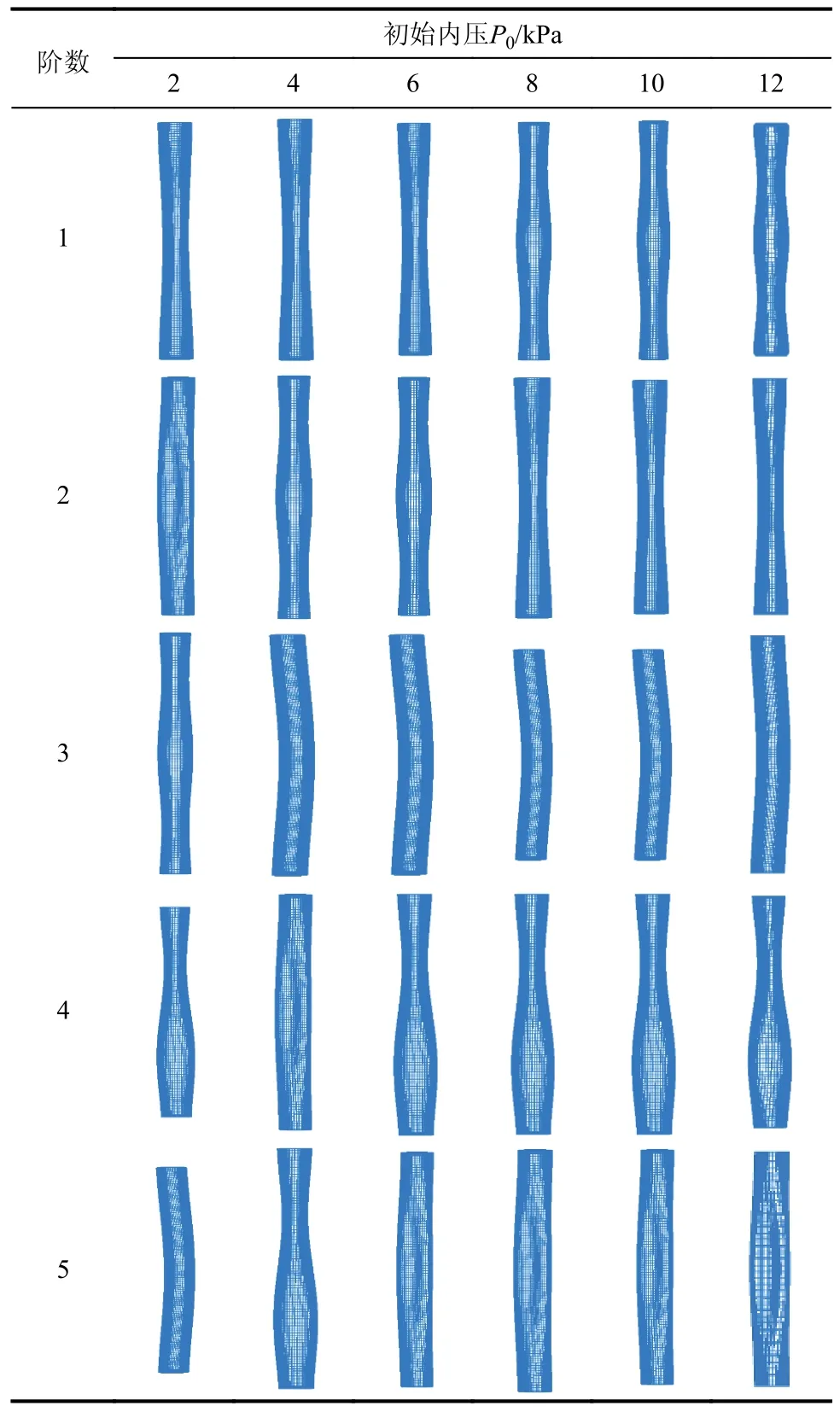
表7 不同初始内压情况下的前5 阶自振模态Table 7 The first five mode shapes for different initial internal pressures

从表7 可以看出，初始内压对充气薄膜管自振模态形状出现阶次的影响较为显著。随着内压的升高，中间凹陷的自振模态从P0≤6 kPa 的第1 阶推后到P0>6 kPa 的第2 阶；单侧鼓凸的自振模态从P0=2 kPa 的第2 阶推后到P0=4 kPa 的第4 阶以及P0≥6 kPa 的第5 阶；中间鼓凸的自振模态从P0=2 kPa 的第3 阶提前到4 kPa≤P0≤6 kPa 的第2 阶以及P0≥8 kPa 的第1 阶；上部凹陷下部鼓凸的自振模态从P0=2 kPa 第4 阶推后到P0=4 kPa的第5 阶，然后又提前到P0≥6 kPa 的第4 阶；整体的弯曲模态从初始内压P0=2 kPa 的第5 阶，提前到P0≥4 kPa 的第3 阶。从表7 还可以看出，当P0≥8 kPa 后，相同自振模态形状的阶次不再发生变化。

但三种模型(即M1、M2 和M3)得到的同一阶次自振模态形状基本相同，所以气-膜耦合作用以及内充气体的附加质量对充气薄膜管的自振模态形状没有明显影响。随着内充气压的升高，外围薄膜管的应力分布发生改变，进而引起充气薄膜管不同位置相对刚度的变化，所以对相同模态形状出现的阶次产生影响作用。

图6 给出了模型M1 和模型M2 的前5 阶频率分别与模型M3 相应频率的比值随初始内压的变化情况。fM1、fM2和fM3分别为由模型M1、模型M2和模型M3 得到的频率，n为频率的阶次。

图6 不同内压下频率比值曲线Fig.6 Ratios of frequencies for different internal pressures

从图6(a)可以看出，初始内压P0≤4 kPa 时，各阶频率比值fM1/fM3未见明显变化，而当P0≥4 kPa后，第1 阶频率比值与第2 阶～第5 阶频率的比值随初始内压增加呈现不同的变化规律：第1 阶频率的比值fM1/fM3随初始内压的升高而逐渐降低；第2 阶～第5 阶频率的比值fM1/fM3均随初始内压的升高而较快增加，但在P0≥ 8 kPa 后又略有降低。

从图6(b)可以看出，初始内压P0≤4 kPa 时，各阶频率比值fM2/fM3均随初始内压升高而略有减小；但当P0≥4 kPa 后，第1 阶频率比值与第2 阶～第5 阶频率的比值随初始内压增加呈现不同的变化规律，与图6(a)所示相应曲线相似：第1 阶频率的比值fM2/fM3随初始内压的升高而逐渐降低，第2 阶～第5 阶频率的比值fM2/fM3均随初始内压的升高先较快增加然后又略有减小，并逐渐趋于稳定。

由于模型M2 考虑了内充气体附加质量的影响，相同初始内压情况下的频率要略低于模型M1的相应频率，但两者随初始内压的变化规律大致相同。模型M1 和模型M2 的自振频率与模型M3 的自振频率平均相差分别为14.73%和10.53%。可见，内充气体附加质量的影响较小，平均为4.20%，而气-膜耦合作用影响则较为显著，平均为10.53%。

充气薄膜管的刚度包括结构刚度Km和气-膜耦合作用产生的刚度Kami两部分。本文中，结构刚度Km是指由于外围薄膜惯性矩、约束条件等因素产生的刚度总和；气-膜耦合作用产生的刚度Kami是指由于内充气体内压和外围薄膜变形之间的耦合作用而产生的刚度。薄膜管刚度Km影响占主导位置而气-膜耦合作用影响较弱，则比值fM1/fM3和fM2/fM3较小，接近于1；薄膜管刚度Kami影响占主导位置，则气-膜耦合作用影响较强，比值fM1/fM3和fM2/fM3远大于1。薄膜管刚度Km和Kami两者在对频率影响作用中所占比重及其变化情况影响fM1/fM3和fM2/fM3的比值曲线形状。随初始内压的升高，刚度Km和Kami均增大，但刚度Km在第1 阶频率中的影响作用中所占比重明显增大，而刚度Kami在第2 阶～第5 阶频率的影响作用中所占比重增大更为显著。因此，fM1/fM3和fM2/fM3的频率比值曲线呈现如图6 所示的变化特征。但当初始内压P0≥8 kPa 后，刚度Kami的影响作用中所占比重基本趋于稳定。

4.2 随长细比的变化

对长细比λ 分别为6、8、10、12、14 情况下的充气薄膜管进行自振特性分析，研究气-膜耦合作用随长细比的变化规律。其他参数同4.1 节。表8所示给出了模型M3 的前5 阶自振模态形状。

表8 不同长细比情况下前5 阶自振模态Table 8 The first five mode shapes for different slenderness ratios

从表8 可以看出，长细比对充气薄膜管自振模态出现阶次的影响较为显著。随着长细比的增加，中间凹陷的自振模态从λ≤8 的第1 阶推后到λ≥10 的第3 阶；中间鼓凸的自振模态则始终为第2 阶，并没有随长细比的增加发生变化；单侧鼓凸的自振模态从λ=6 的第3 阶推后到8≤λ≤10的第5 阶以及λ>10 的更高阶(表8 只给出前5 阶)；整体的弯曲模态从长细比λ=6 的第4 阶，提前到λ=8 的第3 阶以及λ≥10 的第1 阶；长细比λ≥8后，第4 阶出现了充气薄膜管上部鼓凸而下部凹陷的新自振模态，并且随长细比的增加其阶次没有发生变化。此外，当长细比λ=14 时，第5 阶出现“S”形弯曲自振模态，可以预测当长细比进一步增大，“S”形弯曲自振模态的阶次可能会进一步提前。因为充气薄膜管的整体弯曲模态阶次随着长细比的增加而降低，而其局部振动模态的阶次则随长细比的增加而升高。

图7 给出了模型M1 和模型M2 的前5 阶频率分别与模型M3 相应阶次频率的比值随长细比的变化情况。从图7(a)和图7(b)可以看出，模型M2由于考虑了内充气体附加质量的影响，相同长细比情况下要低于模型M1 的相应频率，与模型M3的频率差异略小于模型M1 和模型M3 的频率差异。频率比值fM2/fM3与fM1/fM3平均相差约为4.06%。可见内充气体附加质量对充气薄膜管的自振频率的影响较小。但气-膜耦合作用对自振频率则有显著影响作用，模型M1 和模型M2 的自振频率与模型M3 的自振频率平均相差分别为22.41%和18.35%。

图7 不同长细比情况下的频率比值Fig.7 Ratios of frequencies for different slenderness ratios

从图7(a)和图7(b)中不同阶频率比值的变化曲线可以看出，气-膜耦合作用的影响(fM1/fM3、fM2/fM3比值曲线)随长细比的变化表现出因频率阶次不同而不同的规律：对第1 阶自振频率影响随长细比没有明显变化，但对第2 阶～第5 阶自振频率的影响则随长细比的增加迅速增大。

随长细比的增大，刚度Km和Kami均减小。但在第1 阶频率中的影响作用中，由于Kami的影响减小更快，Km的影响所占比重明显增大；而在第2 阶～第5 阶频率的影响作用中，由于Km的影响减小更快，Kami的影响所占比重增大更为显著。因此，fM1/fM3和fM2/fM3的频率比值曲线呈现如图7 所示的变化特征。

图8 给出了表8 所示第1 阶弯曲模态对应的频率比值fM1/fM3与fM2/fM3随长细比的变化曲线。纵坐标中f表示频率fM1或fM2。气-膜耦合作用对第1 阶弯曲模态的影响(fM1/fM3、fM2/fM3比值曲线)呈现出随长细比的增加而非单调变化的特点。当长细比λ≤8 时，第1 阶弯曲模态在充气薄膜管的自振模态中为第4 阶(λ=6)或第3 阶(λ=8)。根据上一段的分析可知，对于第2 阶～第5 阶频率，刚度Kami的影响更显著，并随长细比的增大其影响作用所占比重逐渐增大，因此，fM1/fM3和fM2/fM3比值曲线呈上升趋势。当λ>8 后，第1 阶弯曲模态跃迁为自振模态的第1 阶。而对于第1 阶频率，刚度Km影响更显著，并且随长细比的变化，其影响作用所占比例始终占主导地位，所以fM1/fM3和fM2/fM3比值曲线会在λ=10 时突然减小，继而随长细比的变化，基本保持不变。

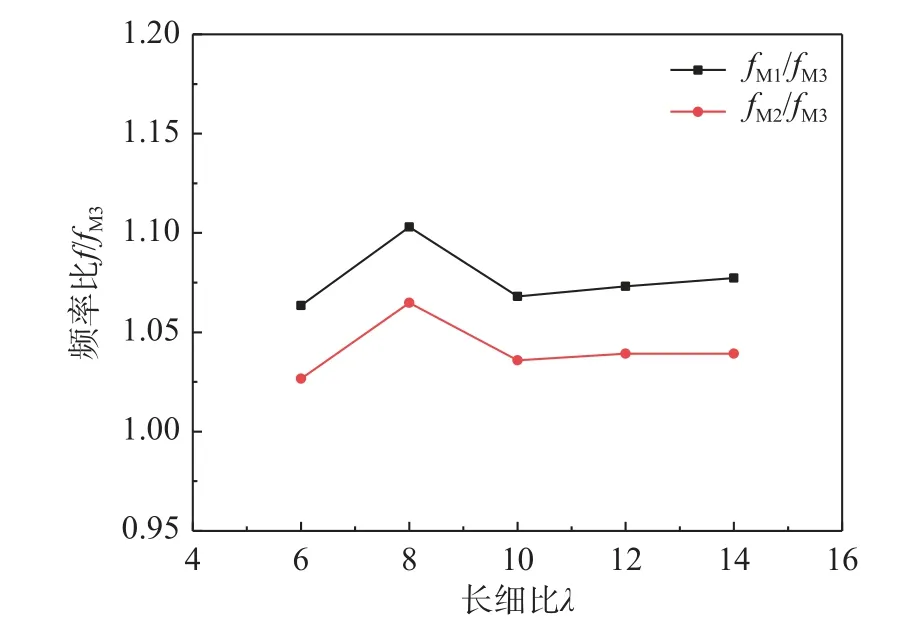
图8 不同长细比情况下对应弯曲模态的频率比值Fig.8 Ratios of frequencies corresponding to the bendingmode shape for different slenderness ratios

4.3 随膜厚的变化

对膜厚分别为0.025 mm、0.050 mm、0.075 mm、0.100 mm 情况下的充气薄膜管进行模态分析，研究气-膜耦合作用随膜厚的变化规律，其他参数同4.1 节。由模型M3 得到的前5 阶自振模态如表9所示。

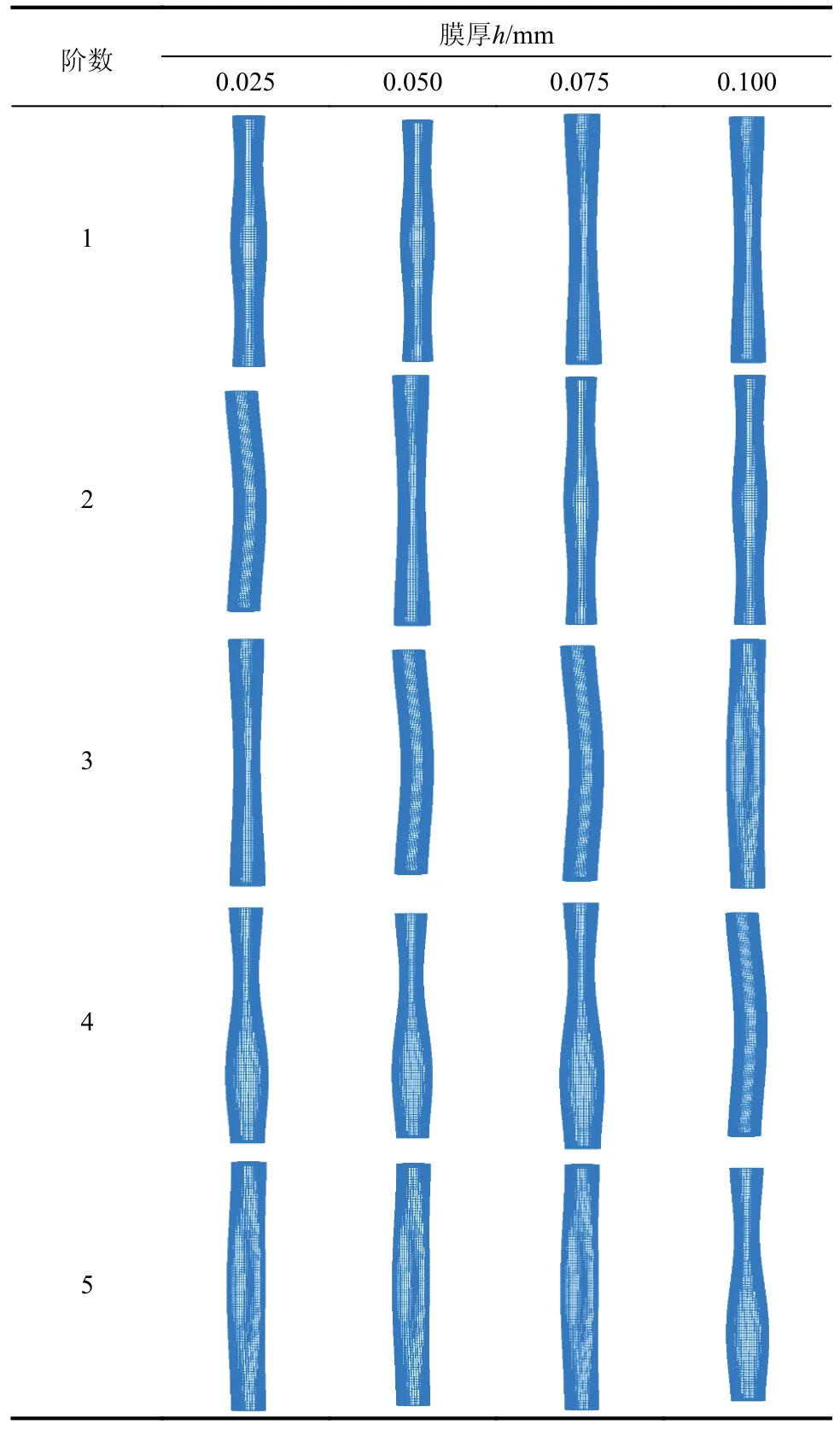
表9 不同膜厚情况下前5 阶自振模态Table 9 The first five modal shapes for different membrane thickness

从表9 可以看出，膜厚对充气薄膜管自振模态出现阶次的影响较为显著。随着膜厚的增加，中间鼓凸的自振模态从膜厚h≤0.050 mm 的第1 阶推后到h≥0.075 mm 的第2 阶；整体弯曲模态从膜厚h=0.025 mm 的第2 阶推后到 0.050 mm≤h≤0.075 mm 的第3 阶以及h≥0.100 mm 的第4 阶；中间凹陷的自振模态从h=0.025 mm 的第3 阶提前到h=0.050 mm 的第2 阶以及h≥0.075 mm 的第1 阶；充气薄膜管上部凹陷而下部鼓凸的自振模态从h≤0.075 mm 的第4 阶推后到h≥0.100 mm 第5 阶；中间局部鼓凸的自振模态从h≤0.075 mm 的第5 阶提前到h≥0.100 mm 第3 阶。

图9 给出了模型M1 和模型M2 的前5 阶频率分别与模型M3 相应阶次频率的比值随膜厚的变化情况。

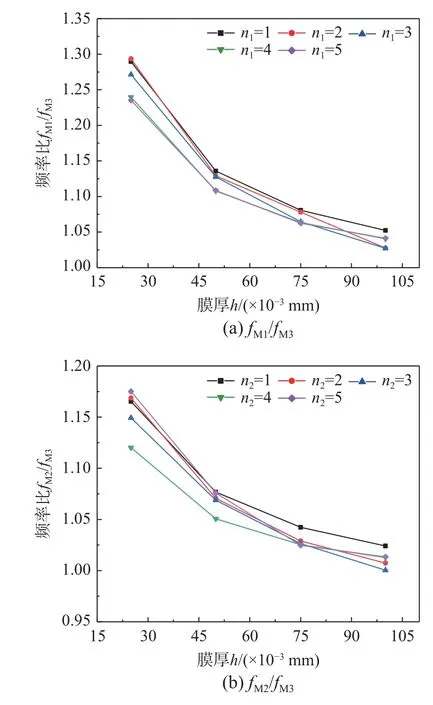
图9 不同膜厚情况下的频率比值Fig.9 Ratios of frequencies for different membrane thickness

从图9(a)和图9(b)可以看出，模型M2 由于考虑了内充气体附加质量的影响，所以相同膜厚情况下的自振频率低于模型M1 的相应频率，与模型M3 的频率差异小于模型M1 和模型M3 的频率差异。频率比值fM2/fM3与fM1/fM3平均相差约为5.75%，可见内充气体附加质量对充气薄膜管的自振频率的影响较小。而气-膜耦合作用影响则较为显著，模型M1 和模型M2 的自振频率与模型M3的自振频率平均相差分别为12.38%和6.63%。

随着膜厚的增加，刚度Km增大，但内充气压和体积均未发生改变，所以Kami不变，因而在对频率的影响作用中，Km影响所占比重明显增大，Kami影响所占比重显著减小。因此，fM1/fM3和fM2/fM3的频率比值呈现如图9 所示的变化特征，即均随膜厚而减小。当膜厚h<0.075 mm 时气-膜耦合作用对自振频率的影响作用仍然处于显著的地位，但当膜厚h≥0.075 mm 后，气-膜耦合作用的影响可以不用考虑。

4.4 随端部约束的变化

对不同端部约束情况下的充气薄膜管进行模态分析，研究气-膜耦合作用随端部约束类型的变化规律。端部约束考虑了两端固定，一端固定一端简支以及两端均简支的情况，其他参数同4.1 节。表10 给出了模型M3 的前5 阶自振模态。

表10 不同端部约束情况下前5 阶自振模态Table 10 The first five modal shapes for different end constraints

从表10 可以看出，端部约束强弱对充气薄膜管自振模态出现阶次的影响较为显著。随着端部约束的减弱，中部凹陷的自振模态从两端固定时的第1 阶推后到一端固定一端简支以及两端简支时的第2 阶；中部鼓凸的自振模态从两端固定时的第2 阶推后到一端固定一端简支时的第3 阶以及两端简支时的第4 阶；整体弯曲自振模态从两端固定时的第3 阶提前到一端固定一端简支以及两端简支时的第1 阶；上部凹陷下部鼓凸的自振模态从两端固定以及一端固定一端简支时的第4 阶推后到两端简支时的第5 阶；中间局部鼓凸的自振模态从两端固定以及一端固定一端简支时的第5 阶提前到两端简支时的第3 阶。

图10 给出了模型M1 和模型M2 的前5 阶频率分别与模型M3 相应阶次频率的比值随端部约束程度的变化情况。

图10 不同端部约束情况下的频率比值Fig.10 Ratios of frequencies for different end constraints

从图10(a)和图10(b)可以看出，模型M2 由于考虑了内充气体附加质量的影响，相同端部约束情况下的自振频率低于模型M1 的相应频率，与模型M3 的频率差异略小于模型M1 和模型M3的频率差异。频率比值fM2/fM3与fM1/fM3平均相差约为5.62%。可见，内充气体的附加质量有一定的影响，但不显著。

随着约束程度的减弱，模型M1、模型M2 的频率与模型M3 的频率的差异增大，从17.50%(模型M1)和12.93%(模型M2)分别增大到51.63%和45.38%。这意味着，气-膜耦合作用对充气薄膜管频率的影响随约束程度的减弱而逐渐增强。

随着约束程度的减弱，刚度Km减小，但内充气压和体积均未发生改变，所以Kami不变，因而在对频率的影响作用中，Km影响所占比重逐渐减小，Kami影响所占比重显著增大。因此，fM1/fM3和fM2/fM3的频率比值呈现如图10 所示的变化特征，即均随约束程度的减弱而增大。

5 结论

本文通过对充气薄膜管在不同内充气体作用等效方式下的动力特性进行有限元分析，研究了气-膜耦合作用对其自振特性的影响及其随初始内压、长细比、膜厚以及端部约束情况的变化规律。取得的主要结论如下：

(1) 气-膜耦合作用以及内充气体的附加质量对充气薄膜管的低阶自振模态没有影响，但初始内压、长细比、膜厚以及端部约束程度的变化会影响同一模态出现的阶次；气-膜耦合作用对自振频率有较显著的影响作用，而内充气体的附加质量对自振频率的影响较小。

(2) 随着初始内压P0的增加，当P0≤4 kPa 时，气-膜耦合作用影响的变化较为平缓，而当P0>4 kPa后气-膜耦合作用影响呈现出因频率阶次不同而不同的规律：对第1 阶频率的影响逐渐降低，而对第2 阶～第5 阶频率的影响则显著增大，但在P0≥8 kPa后影响作用基本保持稳定。

(3) 随着长细比的增加，气-膜耦合作用的影响同样也表现出因频率阶次不同而不同的规律：对第1 阶自振频率影响未见明显变化，但对第2 阶～第5 阶自振频率的影响则迅速增大。

(4) 随着膜厚的增加，气-膜耦合作用的影响快速降低。当膜厚h<0.075 mm 时，气-膜耦合作用仍然处于较显著的地位，但当膜厚h≥0.075 mm后，气-膜耦合作用的影响很小。

(5) 随着端部约束程度的减弱，气-膜耦合作用对充气薄膜管自振频率的影响呈现逐渐增强的变化规律。

本文的研究揭示了气-膜耦合作用对充气薄膜管自振特性的影响规律，有助于深入认识充气薄膜管的动力行为以及动力展开性能，保证充气薄膜结构设计计算的合理性和可靠性。