分离式减震榫的阻尼力模型研究—基于Ramberg-Osgood 模型

魏 标，闵浩峥，汪伟浩,2，李姗姗

(1.中南大学土木工程系，湖南，长沙 410075；2.广东省交通规划设计研究院集团股份有限公司，广东，广州 510440)

分离式减震榫在桥梁抗震设计和实践中取得了良好的抗震效果[1-5]。研究结果表明，分离式减震榫能够很好地限制梁端位移，并满足高铁对行车要求。研究中常采用双线性本构来描述金属阻尼器的力学性能[6-8]。然而针对双线性本构能否描述分离式减震榫在高烈度近断层地震动作用下的力学行为的相关研究较少。同时，往复荷载作用下低碳钢的本构关系较为复杂，呈现出依赖于加载历程的包辛格效应，棘轮效应和循环强弱化效应等非常重要的强非线性特征[9-11]。基于理想弹塑性本构推导的分离式减震榫的骨架曲线，并不能和试验结果相吻合[12]。为了得到能反映分离式减震榫力学性能的骨架曲线数据，往往需要进行试件的拟静力试验，消耗很高的成本。总而言之，目前很少有文献从材料层次出发，研究分离式减震榫的力学性能。缺乏准确高效的描述分离式减震榫力学性能的相关模型，造成了分离式减震榫的耗能性能评估、参数优化设计以及低周疲劳分析等多方面的困难。

1943 年，RAMBERG 和OSGOOD[13]提出一种光滑模型(简称R-O 模型)，来描述低碳钢在循环荷载作用下的应力-应变骨架曲线，如式(1)所示：

式中：K＇为循环强化系数；n＇为循环强化指数，均为控制骨架曲线形状的参数。HIROMASA[14]基于R-O 模型讨论了剪力对等截面梁的影响。SZULADZINSKI[15]基于 R-O 模型推导了等截面梁在塑性铰区域的弯矩-曲率公式。LANZAGORTA[16]基于R-O 模型推导了等截面悬臂梁受剪时的变形公式。李冀龙等[17]基于 R-O 模型，建立了X 型钢板阻尼器的阻尼力模型。结果表明，该模型相较于双线性强化模型更加能够拟合阻尼器实际的滞回曲线。文献[7, 18 - 19]的研究则表明，R-O 模型能很好地拟合低碳钢在逐级对称加载作用下的应力-应变骨架曲线。

本文基于R-O 模型，推导了分离式减震榫骨架曲线的计算方法，并与金属材料有限元仿真中常用的Chaboche 混合强化模型[20]下的计算结果进行比较。随后，基于该方法，提出一种双线性模型的简化算法。并以一座通用的32 m 高铁简支梁桥为背景，讨论近断层脉冲地震动作用下双线性模型的适用性。

1 简化力学模型

当分离式减震榫上、下两端发生相对位移时，可利用对称性取其一半进行分析。根据等强度梁理论[2]，分离式减震榫的几何计算模型如图1所示。榫身横截面为圆形，根据直径变化方式，分为耗能段和传力段。其中：L为榫身高度；L1为过渡段高度；x为榫身横截面到传力段顶端的距离。截面直径d(x)的计算见式(2)：

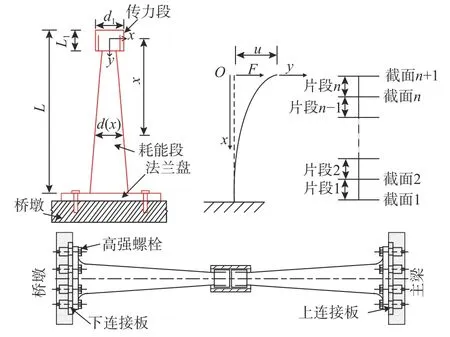
图1 分离式减震榫示意图Fig.1 Diagram of separated shock absorber

式中：d1为传力段直径；a为截面系数。

在小变形情况下，分离式减震榫竖向变形较小，受力特征与悬臂梁类似，只考虑弯矩作用产生的变形。假定分离式减震榫的横截面弯曲变形后仍保持为平面，且仍与变形后的截面轴线垂直。

1.1 力学参数计算方法

1.1.1 弹性刚度

当材料处于线弹性阶段时，由结构力学计算理论，可求解出分离式减震榫的刚度为：

式中：M0(x)为单位荷载作用下，距装置顶端x处截面承受的弯矩值；E为弹性模量；I(x)为截面惯性矩。

1.1.2 骨架曲线

当分离式减震榫处于小变形状态时，可采用一种简化计算方法来计算分离式减震榫骨架曲线，计算步骤如下：

1) 将分离式减震榫平均划分n段，每一段高度为t=L/n，如图1 所示。假定每一段的截面直径hi和曲率ki保持不变。

2) 在传力段顶端施加给定水平力F，得到任意第i个截面的弯矩Mi,

3) 联立式(2)、式(5)和式(1)，通过二分法求出任意截面的曲率ki(见式(6))。

4) 根据各个截面曲率即可求出分离式减震榫的位移u：

上述求解分离式减震榫骨架曲线的计算方法可根据图2 自编程序实现电算。

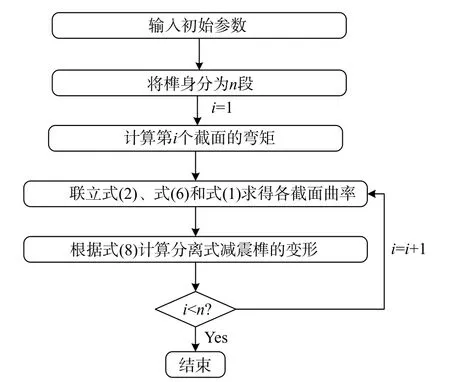
图2 骨架曲线计算流程图Fig.2 Flow chart of skeleton curve calculation

2 双线性模型简化算法

为了给工程设计提供简洁并具有一定精度的参考公式，方便有限元模拟分析，目前工程中多采用双线性模型来描述分离式减震榫的骨架曲线[21]，如图3 所示。

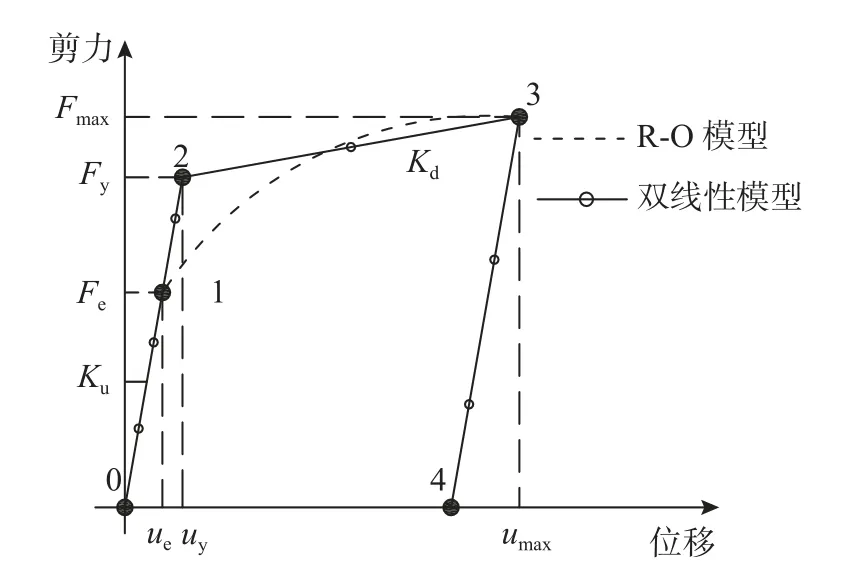
图3 理论滞回模型Fig.3 Theoretical hysteretic model

图3 中：点1 为弹性极限点；点2 为弹性直线延长段与屈服后平台段延长线的交点，即屈服点；点3 为减震榫的设计极限位移点；ue、uy和umax分别为弹性极限位移、屈服位移和极限位移；Fe、Fy和Fmax分别为弹性极限荷载、屈服荷载和极限荷载；Ku为弹性刚度；Kd为屈服后刚度；α为屈后刚度比，且Kd=αKu。

根据图2 中的计算流程，可得到分离式减震榫的骨架曲线，随后便可以在给定极限位移的情况下，将该骨架曲线等效为双线性本构骨架曲线。等效过程如下：

1) 假定分离式减震榫的屈服点 (uy,Kuuy)，从而确定双线性本构骨架曲线的形状。

2) 假定第一象限0234 的面积Ac和理论滞回环0134 面积的At相等，根据式(8)计算两者之间的误差t。

3) 如果t小于容许误差t0，则认为该等效成立，否则改变uy的值，返回第一步重新计算。本文去容许误差t0=1。

4) 确定uy后，根据屈服点和正峰值点数据，从而确定等效后的屈服后刚度Kd。等效过程可以根据图4 自编程序以实现电算。

图4 滞回模型简化流程图Fig.4 Simplified flow chart of hysteresis model

3 R-O 模型正确性验证

为了验证上述公式的正确性，通过建立ABAQUS有限元分析模型进行计算，并与理论结果进行对比验证。分离式减震榫的几何参数按照文献[2]选取，其中，L=370 mm，L1=40 mm，d1=60 mm，a=11.404。采用C3D8R 实体单元进行几何建模，如图5 所示。

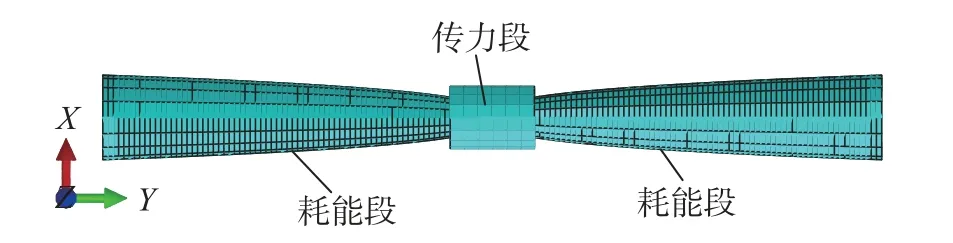
图5 分离式减震榫有限元模型Fig.5 Finite element model of separated shock absorber

文献[19]通过试验对比了常用的LYP225 在循环荷载和单轴拉伸荷载作用下的力-位移曲线。

试验结果显示，LYP225 在循环荷载下的应力-应变曲线与单轴拉伸应力-应变曲线有了较大的区别；通过Chaboche 本构和R-O 模型能够较好地描述LYP225 钢材在循环荷载作用下的应力-应变滞回曲线和骨架曲线。其中：LYP225 的弹性模量E为160 000 MPa，屈服强度为199 MPa；R-O 模型的参数取值为n' =0.24，K'=400 MPa；Chaboche本构等向强化和随动强化的相关参数如表1 所示。其中： σ|0为0.01%塑性应变时应力；Q∞为屈服面半径的最大变化值；b为屈服面半径随塑性应变增加的变化率；Ck为第k(k=1, 2, 3, 4)个背应力的最大变化值； γk为第k个背应力水塑性应变增加的变化率。图6 为基于Chaboche 本构、R-O 模型和理想弹塑性本构计算得到的应力-应变关系对比图。从图中可以看出在小应变状态下Chaboche 本构和R-O 模型计算得到的应力-应变骨架曲线基本能够重合，并且和理想弹塑性本构骨架曲线相差较大。

表1 Chaboche 本构参数标定表Table 1 Parameters of Chaboche constitutive model

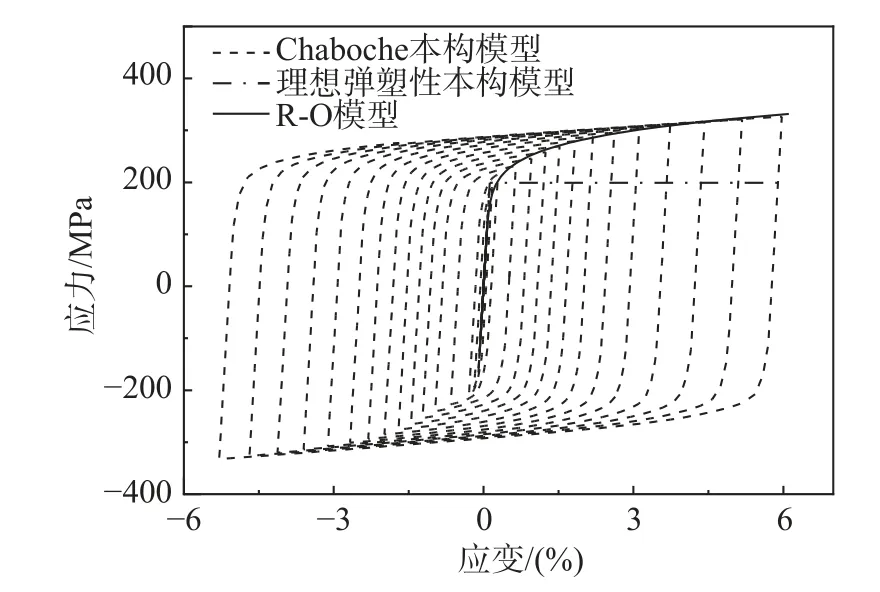
图6 应力-应变曲线对比图Fig.6 Comparison of stress-strain curves

为准确模拟减震榫拟静力试验，在ABAQUS中对榫身底部采用固结约束，定义传力筒和榫头为硬接触，不考虑接触过程中的摩擦力作用。控制分离式减震榫顶部在x方向进行平动加载，加载历程如图7 所示。

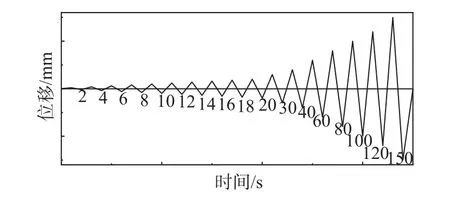
图7 加载制度Fig.7 Loading scheme

图8 为分离式减震榫基于Chaboche 本构，R-O模型和理想弹塑性本构计算得到的骨架曲线对比图。从图中可以看到，在150 mm 极限位移以内，Chaboche 本构和R-O 模型计算所得到的骨架曲线基本吻合，而理想弹塑性本构无法描述分离式减震榫进入弹塑性状态后的力学性能，从而验证了骨架曲线理论推导公式的正确性。图9 为分离式减震榫基于Chaboche 本构和理想弹塑性本构得到的滞回曲线和基于R-O 骨架曲线简化得到的双线性本构滞回曲线的对比图。从图中可以看出，在位移加载逐级递增的过程中，双线性本构能够更好地描述在实际正向加载和反向加载过程中任意特定位移下的力的大小，同时双线性本构下每一圈滞回面积也更加接近实际的滞回耗能。当位移幅值较小时，低碳钢的等向强化效应并不明显，以随动强化为主，此时双线性本构滞回面积要大于Chaboche 本构滞回面积，而随着位移幅度增大，等向强化效应逐渐占据主导地位，Chaboche本构滞回面积开始大于双线性本构的滞回面积。

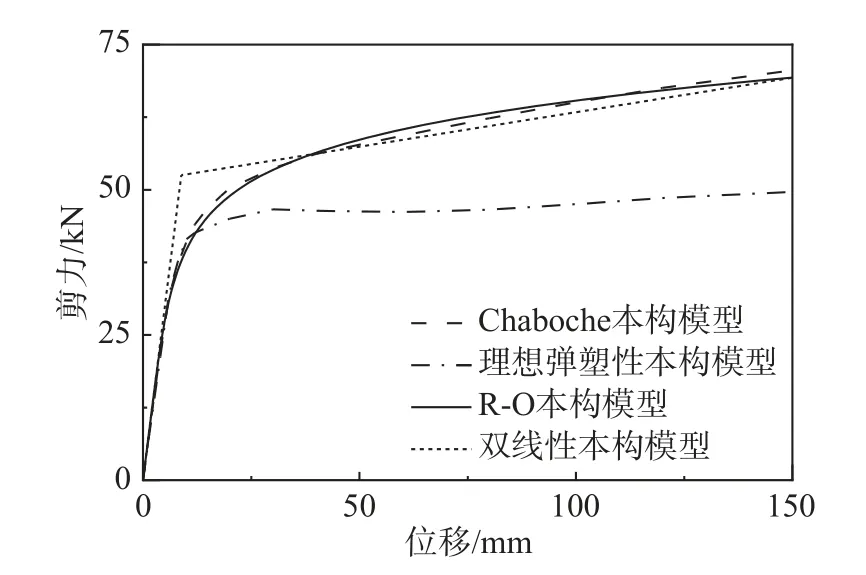
图8 骨架曲线对比图Fig.8 Comparison of skeleton curves

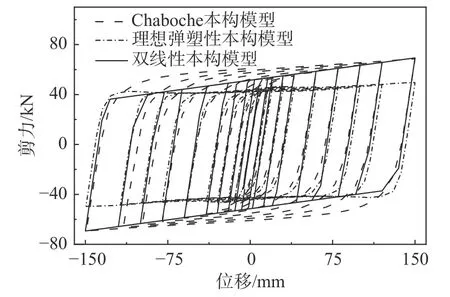
图9 滞回曲线对比图Fig.9 Comparison of hysteretic curves

4 双线性简化滞回本构适用性评估

虽然双线性本构能够较好描述在逐级对称加载作用下的分离式减震榫的力学性能，然而在实际工程中桥梁所受到的循环荷载往往不完全对称。尤其是在具有脉冲效应的高烈度近断层地震动作用下，根据不同的材料滞回本构模型得到的弹塑性地震反应结果可能会存在不可忽视的差异，双线性本构用于桥梁结构的弹塑性地震反应分析的适用性仍然有待仔细评估。

4.1 桥梁建模

4.1.1 主梁

本文桥梁计算模型选取一座通用的32 m 双线铁路预应力混凝土简支梁桥。主梁为后张法预应力混凝土双片T 型梁[22]。每2 片单独的T 型梁之间采用横隔板连接，沿纵桥向每4 m 1 个。截面设计尺寸参考《通桥(2012)2201-I(32 m)》设计图纸，如图10 所示。T 型梁上翼缘宽2.28 m，下翼缘宽0.88 m，腹板宽2.4 m，梁高2.7 m。混凝土材料的强度等级为C55。根据设计图纸，主梁自重为297.6 t，二期恒载为101.26 t/m。

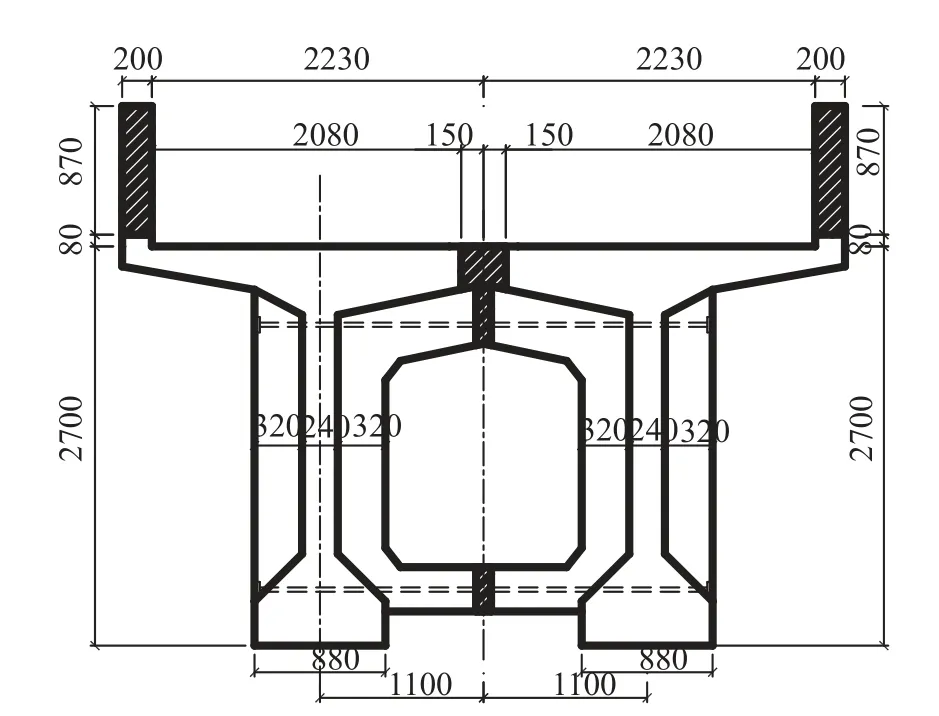
图10 主梁横截面 /mmFig.10 Cross-section of main girder

过往对于桥梁震害的调查资料都表明，主梁在强震下仍然保持弹性状态[23-26]，因此忽略钢筋和预应力筋，采用C3D8R 实体单元模拟主梁，将混凝土材料设置为弹性，其弹性模量为36 000 MPa，泊松比为0.2。将轨道结构模拟为等质量、体积大致相等的实体，附加在主梁上。

4.1.2 桥墩

桥墩采用9 m 墩高的变截面圆端形实心桥墩。桥墩混凝土材料采用C35 混凝土，纵筋采用HRB400。桥墩构造示意图如图11 所示，桥墩截面的配筋率在0.2%～0.3%。通过C3D8R 实体单元模拟桥墩，在墩底1/3 墩高范围内向下逐渐加密网格。混凝土本构采用ABAQUS 内置的混凝土塑性损伤模型进行模拟。受压恢复因子wc和受拉恢复因子wt分别按默认值取为1 和0，混凝土具体的本构关系如图12 所示。钢筋材料的本构采用理想弹塑性本构进行模拟。钢筋和混凝土的相互作用类型为“内置区域”约束，不考虑混凝土和钢筋的粘结滑移效应。TSOPELAS 等[27]在研究中指出，在硬土地区桩土相互作用对隔震支座的基础振动周期是可以忽略不计的。为了减小数值计算的负担，同时控制对无关因子对数值计算结果的影响，假定桥墩底部的约束为固结约束，不考虑桩土相互作用。

图11 桥墩构造 /mmFig.11 Pier structure

图12 混凝土拉压损伤本构 /mFig.12 Damage constitutive relationship of concrete

4.1.3 支座建模

摩擦摆支座组合金属阻尼器已经成为近断层抗震中常用的组合减隔震措施[22,28]。在每一跨主梁的两端分别布置2 个摩擦摆支座和14 根分离式减震榫，如图13 所示。摩擦摆支座的等效半径取1500 mm，摩擦系数假定为0.02[28]。分离式减震榫的实体单元建模如图5 所示。通过绑定约束将分离式减震榫底部和桥墩顶部固结，通过MPC 约束固结传力筒和主梁底部，随后通过面面接触定义传力筒和分离式减震榫之间的接触关系，从而以此限制主梁和桥墩之间的相对位移。通过设置3 种本构进行对比分析。首先通过ABAQUS 内置的Chaboche 本构模拟分离式减震榫在实际工作过程中的力学行为[29]，其参数标定如表1 所示。作为对比，通过在主梁和桥墩之间设置笛卡尔连接器来描述图9 的双线性本构的力学行为从而检验滞回模型简化算法的适用性，以及通过定义分离式减震榫的材料为图6 中理想弹塑性本构来对比忽略各向同性强化效应对计算结果造成的影响。

图13 铁路简支梁桥有限元模型Fig.13 Finite element model of simply-supported railway bridge

4.1.4 地震波输入

根据《铁路工程抗震设计规范》[30]中的目标反应谱，从美国太平洋地震工程研究中心(PEER)数据库中选取了7 条适合Ⅱ类场地的近断层脉冲地震动记录[31]。由于该桥梁位于9 度地区，考虑到遭遇罕遇地震的情况，分别将各条波的峰值加速度调整为0.64g，并沿纵桥向输入。所选地震波参数见表2。将七条地震波的加速度反应谱转化成动力放大系数β 曲线，并在调整后与目标反应谱进行对比，如图14 所示。

表2 输入地震记录特征Table 2 Characteristics of selected earthquake records

4.2 支座位移对比

选取P2 桥墩的摩擦摆支座在1 号地震作用下的位移时程进行详细分析，如图15 所示。从图中可以看出，近断层地震动的速度脉冲导致支座出现较大的位移冲击，这使得理想弹塑性本构和Chaboche 本构下计算出来的支座位移在t=11.4 s和t=12.2 s 处出现了明显的偏差。图16 为分离式减震榫在三种本构下的滞回曲线对比图。由图16可得，由于在每一次滞回过程中，分离式减震榫按照非等幅加载进行滞回，各项同性强化效应不明显。双线性本构下的分离式减震榫的剪力总是偏大，从而导致其支座位移偏小于Chaboche 本构下的支座位移，如图16 中t=11.4 s 时所示。而在大幅值变形过程中则相反。如在t=12.2 s 时，各项同性强化效应占据主导，Chaboche 本构下的剪力与双线性本构下的剪力接近，进而双线性本构下支座位移与Chaboche 本构下的支座位移接近。理想弹塑性本构则完全忽略了低碳钢在循环荷载作用下的各向同性强化特性，进而严重低估了分离式减震榫的变形剪力。故而，基于理想弹塑性本构得到的支座位移峰总是偏大。表3 给出了基于不同本构下的P2 桥墩位移峰值的对比，其中Difference1 和Difference2 分别表示了双线性本构和理想弹塑性本构下支座位移峰值与Chaboche 本构支座位移峰值的误差百分比。由于双线性本构所计算的支座位移峰值相较于Chaboche 本构所计算的结果的平均误差能够控制在5%以内，基本能够保证基于双线性模型得到的计算结果的安全性，而基于理想弹塑性本构计算所得到的支座位移峰值相较于Chaboche 本构所计算的结果的平均误差高达18.13%，并不适用于描述实际工程应用中的分离式减震榫的工作性能。

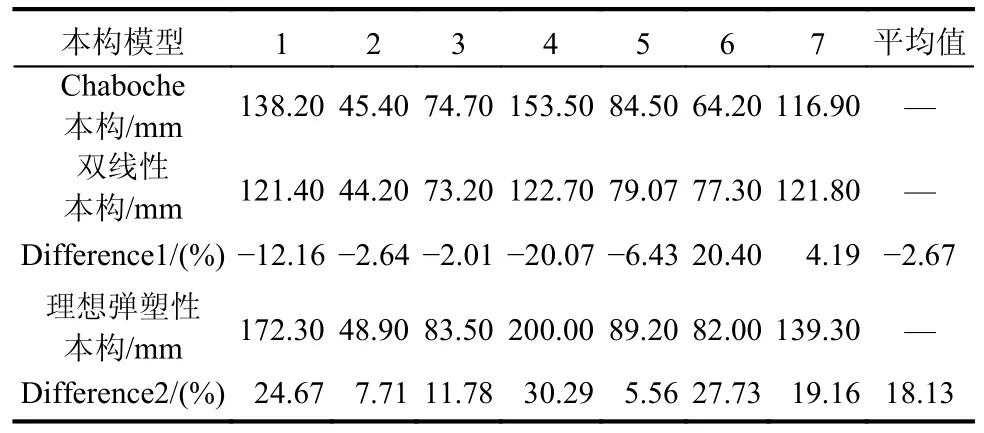
表3 P2 支座位移时程最大值比较Table 3 Comparison of peak displacement of P2 bearing

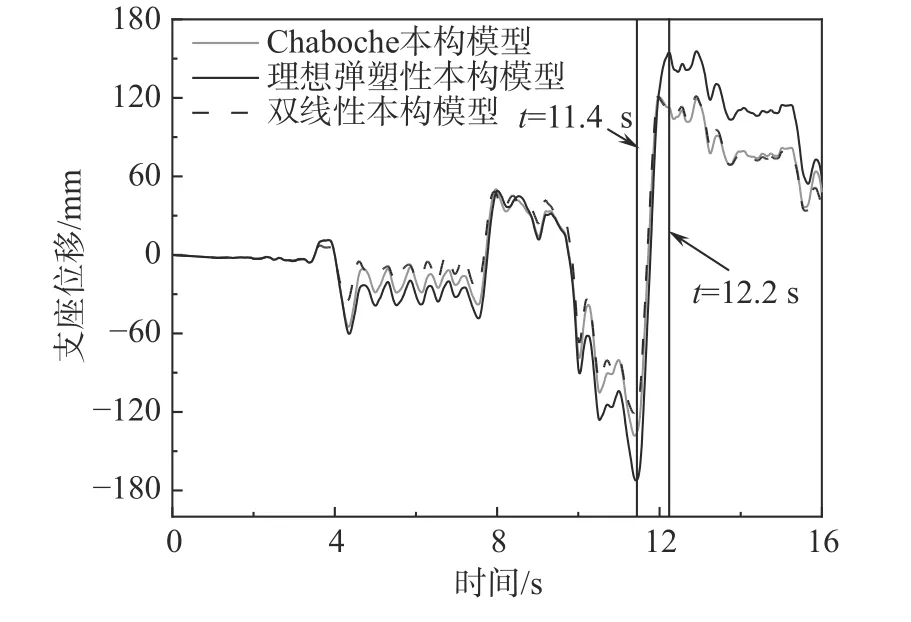
图15 支座位移时程对比Fig.15 Comparison of bearing displacement time history

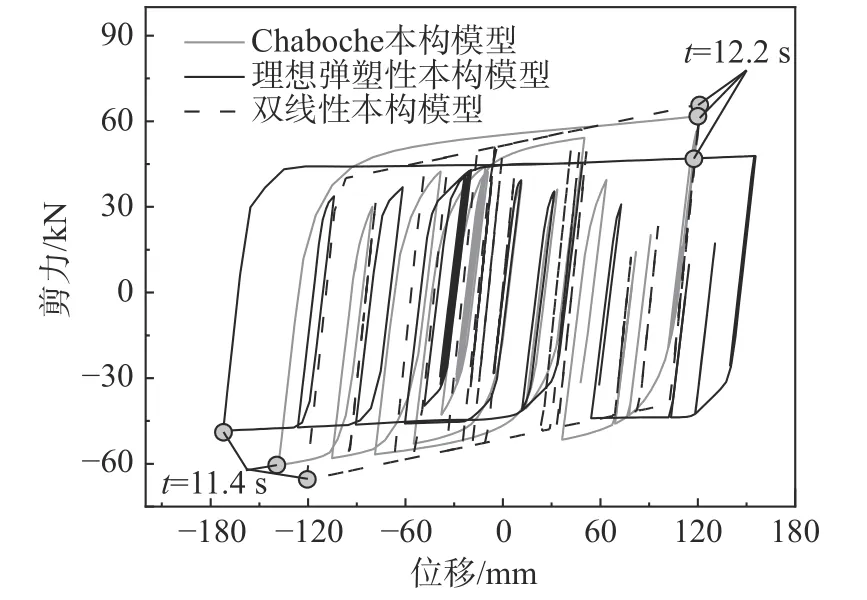
图16 分离式减震榫滞回曲线对比图Fig.16 Comparison of hysteretic curves of separated shock absorber

4.3 墩底弯矩对比

图17 为P2 桥墩在1 号地震下墩底弯矩时程对比。从图中可以看出，三种本构模型计算得到的墩底弯矩时程基本一致，其原因是由于在罕遇近断层地震动作用下，墩底已经出现了混凝土裂缝和钢筋屈曲。表4 为不同本构下P2 桥墩墩底弯矩峰值对比。从表4 可以看出，双线性本构计算所得到的墩底最大弯矩总是偏大，而理想弹塑性本构计算所得到的墩底最大弯矩总是偏小，这说明基于双线性本构计算所得到的墩底弯矩时程是偏于安全的。

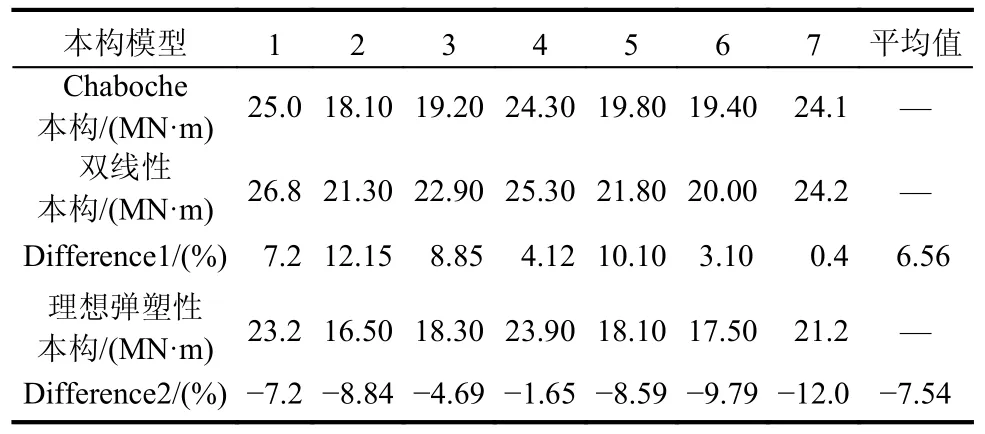
表4 P2 墩底弯矩峰值比较Table 4 Comparison of peak bending moment at pier bottom of P2

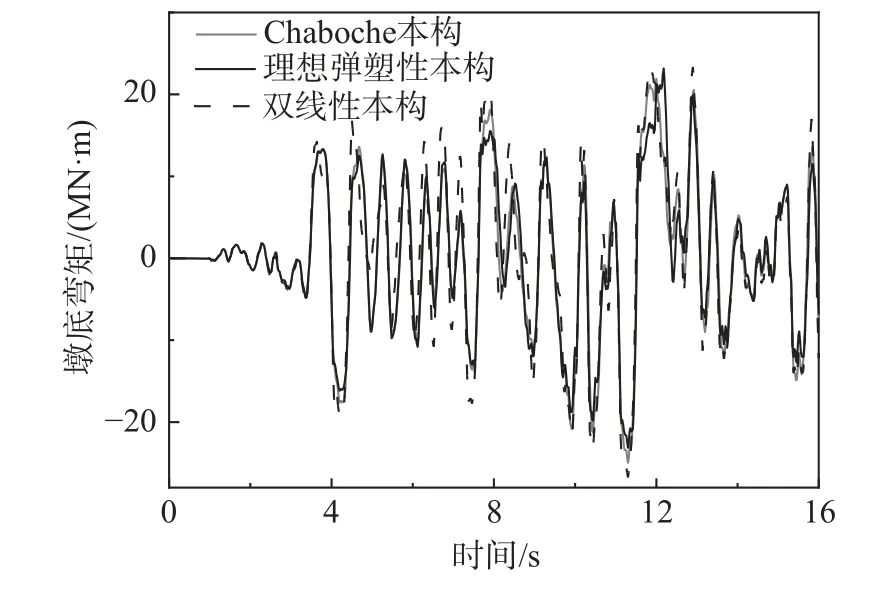
图17 墩底弯矩时程曲线对比图Fig.17 Comparison of pier bottom bending moment time history

5 结论

本文基于R-O 模型进行了分离式减震榫的阻尼力模型研究，通过理论分析和数值模拟得到如下结论：

(1) 基于R-O 模型推导了分离式减震榫的力-位移骨架曲线的计算方法。计算结果表明，在设计位移以内，基于R-O 模型计算所得到的骨架曲线能够较好地吻合Chaboche 本构下分离式减震榫的骨架曲线。

(2) 提出一种双线性本构的简化方法。ABAQUS拟静力计算结果表明，双线性本构能够较好地拟合Chaboche 本构下的滞回曲线。在分离式减震榫位移较小时，双线性滞回曲线所围成的滞回面积大于Chaboche 本构下的滞回面积；随着变形的增大，Chaboche 本构下的滞回面积逐渐大于双线性滞回曲线所围成的滞回面积。

(3) 在近断层脉冲地震动作用下，双线性本构计算得到的支座位移时程能够较好拟合Chaboche本构计算所得到的支座位移时程。两者计算得到的支座位移峰值的平均误差可以控制在5%以内。基于双线性本构所得到的墩底最大弯矩，普遍偏大于Chaboche 本构下计算得墩底最大值弯矩，并且其平均误差能够控制在10%以内。本文提出的双线性滞回本构的简化方法用于工程计算是安全且合理的，基于R-O 模型的双线性模型简化算法能够适用于高烈度地区近场脉冲地震动作用下的抗震设计。