基于高性能桩单元法的海上风机单桩支撑结构水平承载力研究

张舒烨，刘思威，马会环

(1.中山大学土木工程学院，广东，珠海 519082；2.香港理工大学土木及环境工程学系，香港 999077)

1 研究背景

海上风电机由机舱叶轮、下部结构和基础组成[1]。其支撑结构往往采用大直径单桩基础，约占已投入使用基础形式的80%[2]。单桩支撑结构下部基础插入土体深部以获得足够的水平抗力，上部塔筒根据弯矩沿其高度的变化规律常常设计为锥形。然而由于海上风电机尺寸巨大，给支撑结构的设计施工带来了巨大的挑战，从而极大地提高了支撑结构成本，其成本已占到总成本的20%～30%[3]。

数值分析是单桩支撑结构设计中的关键一环，单桩支撑结构的主要数值分析主要基于实体单元模型和基于离散弹簧法的梁单元模型[4]，二者的原理如图1 所示，在实际工程设计中，单桩基础常常被简化为文克勒地基梁模型，使用连接在梁上的一组刚度不同的弹簧(p-y曲线)表示桩土相互作用，因此这种方法被称为p-y曲线法，通过在单元节点上连接非线性弹簧来定义桩土相互作用的方法被称为离散弹簧法，在选择合适的p-y曲线以及划分足够多单元的前提下，通过该方法得到的桩基水平响应将与实体单元法具有较好的一致性[5]。

基于地基梁模型，许多学者提出了许多不同形式并适用于不同土质的p-y曲线。在砂土方面，MCCLELLAND 和FOCHT[6]首次提出了砂土的p-y曲线，REESE 等[7]提出的直曲线形式的柔性桩砂土p-y曲线模型被应用于早期的API 规范[8]中，此后，诸多学者提出了包括双折线[9]、抛物线[10]、双曲线[11]等形式在内的砂土p-y曲线。在粘土方面，MATLOCK[12]、REESE 和WELCH[13]分别提出了适用于硬粘土与软粘土的p-y曲线。SULLIVAN等[14]则在此基础上提出了一种统一化方法，以适应于任何类型的粘土。河海大学的王惠初等[15]也基于邓肯模型提出了一种新的粘土p-y曲线统一法。

在诸如海上风电桩基等大直径桩的工程设计中，学界发现。传统p-y曲线逐渐显现出了不适用性[16]，并对适用于大直径桩的p-y曲线开展了研究。YAN 和BYRNE[17]、KIM 等[11]指出，API 规范中推荐的p-y曲线会显著高估土体的初始刚度，使得设计偏于不安全。针对上述问题，一些研究者对传统p-y曲线进行了修正，以使其适用于大直径桩情况[18-20]，也有部分学者认为，基于静力触探(CPT)的p-y曲线能够适用于大直径桩计算，这是由于相关文献[21 - 22]指出，CPT 中的的土层锥尖阻力qc主要取决于水平方向有效应力，认为可以通过土层锥尖阻力qc来反过来研究水平土抗力的特性，因此周全智等[23]在数值模拟中引入了基于CPT 的p-y曲线以考虑桩基大直径的影响。

现有p-y曲线研究结果大大便利了海上风机单桩支撑结构的设计计算，但海洋土体往往具有分层、参数随土体深度变化呈现高度非线性的特点，因此若采用传统的离散弹簧法，需要布置足够多的离散土弹簧以表征上述非线性，这增大了有限元模型需要划分的单元数量。而同时，对于风机塔筒的锥形结构，常规设计中常考虑使用多段恒截面梁对变截面梁进行等效[24]，这也增大了单元划分量，进一步降低了计算效率。

针对上述问题，LI 等[25]提出了一种考虑土-结构相互作用的欧拉-伯努利梁柱单元，该单元通过在能量方程和切线刚度矩阵中引入桩土作用项实现桩土相互作用关系的内置。在计算时，该单元可以不通过节点施加弹簧，所以无需划分过多单元。并且对于锥形梁，该单元能够考虑截面刚度随梁长增加的变化，无需通过多个均匀截面单元进行等效。以上二者的结合将大大降低在同时考虑锥形梁和桩土作用情况下的单元划分量，进而提高计算效率，因此该单元在后文中以高性能桩单元代称。高性能桩单元与传统单元的比较如图2所示。

本工作基于高性能变截面梁柱单元方法，结合SURYASENTANA 和LEHANE[26]、GUO 等[27]提出的大直径修正p-y曲线，研究了高性能变截面梁柱单元方法在海上风机单桩支撑结构计算中的适用性，并进一步研究了大直径单桩基础的水平承载性能，以期为海上风机支撑结构设计计算提供参考。

2 高性能桩单元分析方法

2.1 基本假设

高性能桩单元分析方法通过以下假定简化单元推导过程及表达式：1) 忽略剪切变形与翘曲变形；2)荷载保守；3)桩身材料均匀且具有各向同性；4)桩单元符合欧拉-伯努利假设。

2.2 单元形函数

已知单元节点的位移如图3 左侧所示，选取单元中点作为坐标系原点，以单元轴向为x轴建立正交坐标系。图中共有12 个参数，参数s代表平移位移、θ 代表转角位移，下标第一项表示位移方向，第二项表示节点编号。对单元中的自由度按照图4 进行压缩，得到单元端部位移和节点力如下式：

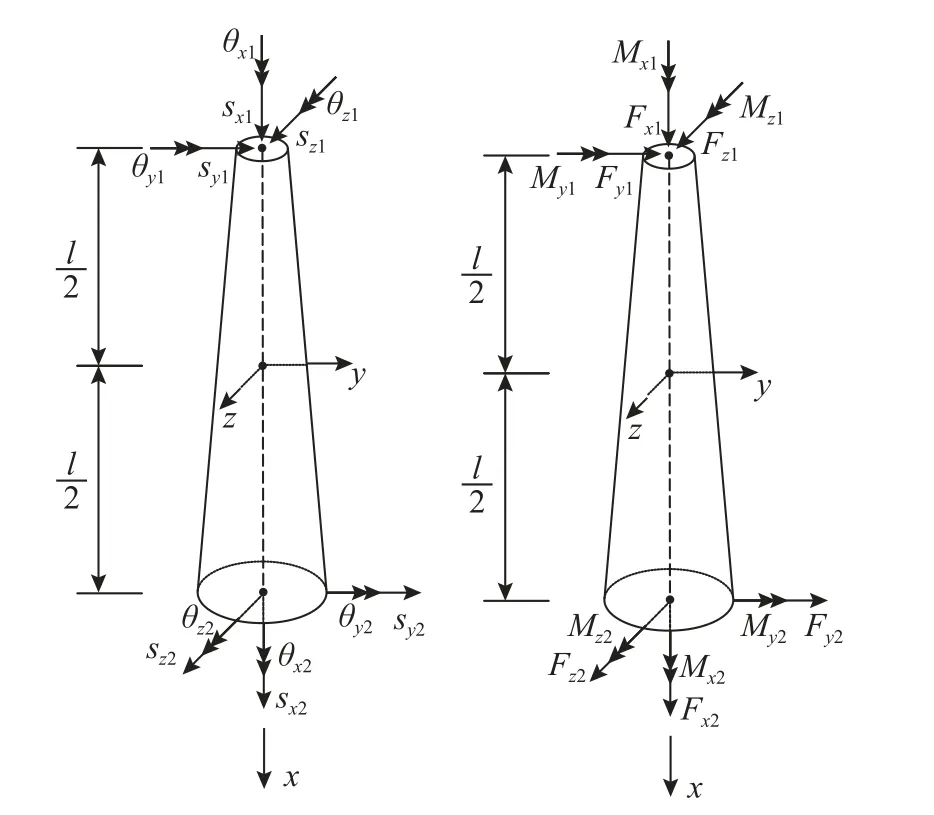
图3 单元节点位移和节点力分量Fig.3 Element node displacement and node force components

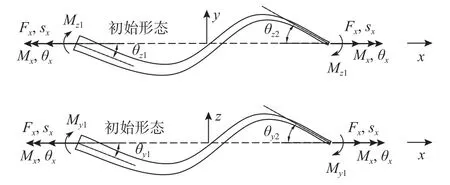
图4 压缩后的单元节点位移和节点力分量Fig.4 Element node displacement and node force components after compression

基于压缩后的位移参数分别使用线性插值和埃尔米特插值方法构建单元形函数，使用节点位移表示沿锥形单元轴向任意一点的轴向、侧向以及扭转位移如下[28]：

2.3 总势能

高性能桩单元法通过在势能表达式中引入土体应变能实现桩土作用的内置计算，其总势能表示如下：

式中：Π 为总势能；UE为单元应变能；US为土体应变能；W为外力作功。

单元应变能可采用式(8)计算：

式中：E为桩体的弹性模量；G为桩体的剪切模量；A(x)为截面面积；Iy和Iz分别为关于y轴和z轴的截面惯性矩；J为极惯性矩。

土体应变能为单元不同深度处的桩侧弹簧储存势能之和，在数值计算中为了得到土体应变能的显示表达式，采用如下的高斯-勒朗德积分表达式计算：

式中：n为高斯积分点的个数；TFL和TFS分别为桩侧水平抗力和竖向摩阻力的圆锥效应系数[29-30]；Wm为第m个高斯点的积分权重；ρm和xm分别为第m个高斯积分点的水平和竖向位移；κρ,m和κx,m分别为第m个高斯积分点的p-y曲线和t-z曲线在相应位移处的切线斜率。

外荷载作功可按式(10)计算：

式中：Fi和si分别为节点两端12 个自由度上每一个自由度可能的外荷载和对应的位移。

最小势能原理表明，结构单元内的全部势能之和总倾向于达到最小，因此可以通过总势能微商为0 的条件建立锥形单元的平衡方程：

2.4 切线刚度

通过对总势能表达式进行二阶变分可以得到有限元分析所需的切线刚度矩阵。高性能桩单元法中的切线刚度矩阵由线性刚度矩阵、几何刚度矩阵和土体刚度矩阵组成，它们的矩阵形式和组合关系如下：

式中：kL为线性刚度矩阵；kG为几何刚度矩阵；kS为土体刚度矩阵；E为桩身弹性模量；L为单元长度；αi、βi为锥形刚度因子；为几何刚度因子，计算式见LIU 等[31]；n为高斯点个数、i为高斯点序号、α 为高斯点权重系数，计算式见LI 等[25]。

整合前述三个矩阵便能够得到总体切线刚度矩阵如下：

2.5 求解方式

高性能桩单元法采用牛顿-拉夫逊法增量迭代算法求解单元刚度方程。并且对于桩受水平荷载时可能产生的大挠度，使用更新拉格朗日描述[32]进行刚度增量逼近，根据最后已知的单元状态建立平衡条件，总变形是通过一系列旋转变换而不是通过求和过程得到的，因此可以考虑任意大的构件变形。

综上，高性能桩单元法能够考虑桩土作用、变截面、大变形等因素，可以较好地满足风机支撑结构的一体化计算需求，因此本文将在验证上述算法正确性的基础之上，对包括桩基和塔筒在内的海上风机单桩支撑结构开展计算分析。

3 算法验证

3.1 单层土体有效性验证

本小节选取均质粉砂层作为桩基埋置土层，大直径钢管桩作为桩基形式进行高性能桩单元的单层土体有效性验证。土层和桩基的参数详见表1 和表2。

表1 单层土体参数[23]Table 1 Single layer soil parameters[23]

表2 桩基参数Table 2 Pile parameters

桩土相互作用方面，本文使用基于静力触探方法(CPT)的p-y曲线以考虑海上风电单桩的大直径效应，其中砂土p-y曲线选择SURYASENTANA和LEHANE[26]基于有限元分析提出的刚性短桩p-y曲线；粘土则选择GUO 等[27]基于实验数据提出的粘土p-y曲线。p-y曲线分别如式(16)和式(17)所示：

式中：pcu为CPT 得到的土层锥尖阻力； σvD'为有效上覆土压力。

1)0≤z≤3时:

2)z>3D时:

式中：p为单位长度土抗力；pcu为CPT 得到的土层锥尖阻力；y为桩体水平位移；pu为极限水平土抗力；D为桩基外径；z为桩深。

根据上述公式计算得到土层不同深度砂土以及粘土的p-y曲线如图5 所示。

综上，对于临床疑诊为TIO，99mTc-HYNIC-TOC SPECT显像结果阴性的患者，68Ga-DOTA-TATE PET/CT可作为补充检查有效地检出TIO致病肿瘤。TIO致病肿瘤68Ga-DOTA-TATE PET/CT图像上均可见生长抑素受体高度表达。另外，同机CT具有一定的特点，骨组织肿瘤局部可见溶骨性骨质破坏或局灶性骨质密度增高，四肢长骨病变常呈偏心性生长，部分累及骨皮质；软组织肿瘤多呈密度均匀等或低密度结节，具有以上影像学特点倾向于TIO致病肿瘤的诊断。

分别使用高性能桩单元和实体单元进行验证计算。其中将高性能桩单元数目划分为8、10、20、40、80 以研究单元数目对计算结果准确性的影响。同时在有限元分析软件中建立基于实体单元的离散弹簧模型，模型共划分3200 个单元，沿着轴向布置80 层弹簧以保证计算结果的准确性。基于上述模型对高性能桩单元的高效性和准确性进行验证。

图6 显示了在50 000 kN 水平荷载，底部固支，不同单元数目下高性能桩单元的水平位移计算结果。可以看出随着单元数目的增加，采用不同单元数目计算得到的水平位移曲线几乎重合，这说明单层土体中，高性能桩单元计算结果几乎不受单元数目影响，对于单元数目的要求是非常低的，具有高效性。而图7 显示了高性能桩单元数目为8 时与实体单元计算结果的对比曲线，两者桩顶水平位移计算结果一致，这验证了高性能桩单元在单层土体中计算的准确性。

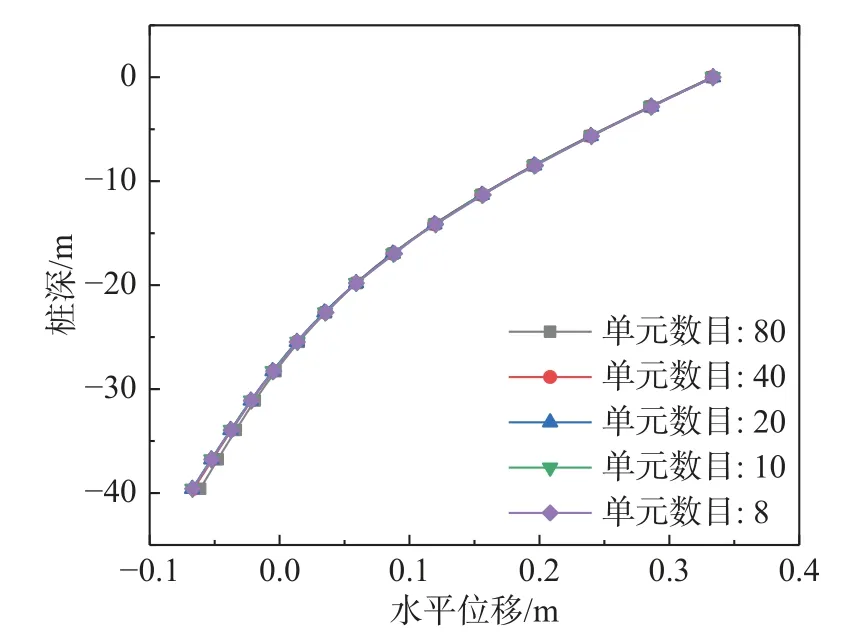
图6 不同单元数目下高性能桩单元水平位移曲线Fig.6 Horizontal displacement curve of efficient element under different number of elements

3.2 多层土体有效性验证

分层土体中的p-y曲线相对于单层土体具有更高的非线性。在离散弹簧单元法中常通过增加弹簧和单元数量来考虑土体高度非线性的影响，从而增加了计算成本。而高性能桩单元法将土体抗力集成在单元内部，单元划分不受土弹簧布置密度的影响，减少了单元划分量，因此能够提高非线性问题的计算效率。

研究选取淤泥层-黏土层-粉砂层作为桩基埋置土层，假设土层的每一层未均质，土层参数参见表3，桩基参数见表2。桩土相互作用基于2.1 节中的p-y曲线得到。

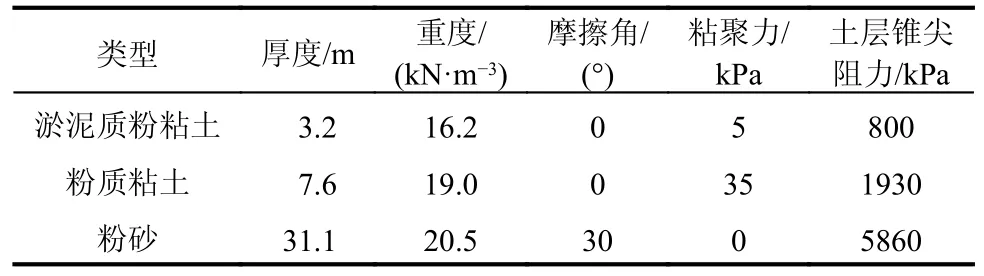
表3 多层土体参数[33]Table 3 Multi layer soil parameters[33]

高性能桩单元数目分别划分为10、20、40、80；同时将实体单元分别置于10 层弹簧和80 层弹簧的条件下进行计算，以对比土壤高度非线性下不同单元计算结果受单元数目影响的差异。

水平荷载下的计算结果对比如图8 所示，可以得知在高度非线性土体下，高性能桩单元计算结果仍几乎不受单元数目影响，且与80 层弹簧下的实体单元计算结果符合良好。反观实体单元模型，当弹簧布置层数为10 时，水平位移计算结果显著偏大，需要划分更多节点才能获得满足精度的计算结果，这从侧面验证了高性能桩单元于复杂土体中计算的优越性。

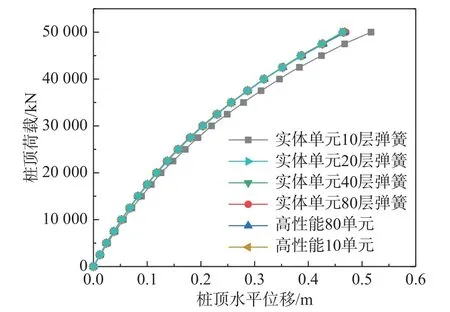
图8 不同单元数目下两类单元水平位移-荷载对比曲线Fig.8 Lateral displacement-load curve of two kinds of element under different element number

3.3 海上风机支撑结构算例验证

本小节使用高性能桩单元对简化的风机支撑结构进行计算。首先将风机支撑结构简化为锥形圆筒和定截面圆筒的组合，分别用于模拟塔筒和单桩，塔筒和单桩均采用高性能单元进行模拟，因此不同组件间采用单元节点进行连接。 模型的几何参数如表4 和图9 所示，基础埋置土层参数参照某风电场地质数据[23]选取，如表5 所示。采用高性能桩单元进行计算，将结构划分为7 个单元，其中塔筒段使用5 个单元，基础段使用2 个单元。同时设置基于离散弹簧法的实体单元模型进行对比验证，实体单元模型如图10 所示，包含61 161 个单元。

表4 风机支撑结构参数Table 4 Parameters of wind turbine support structure

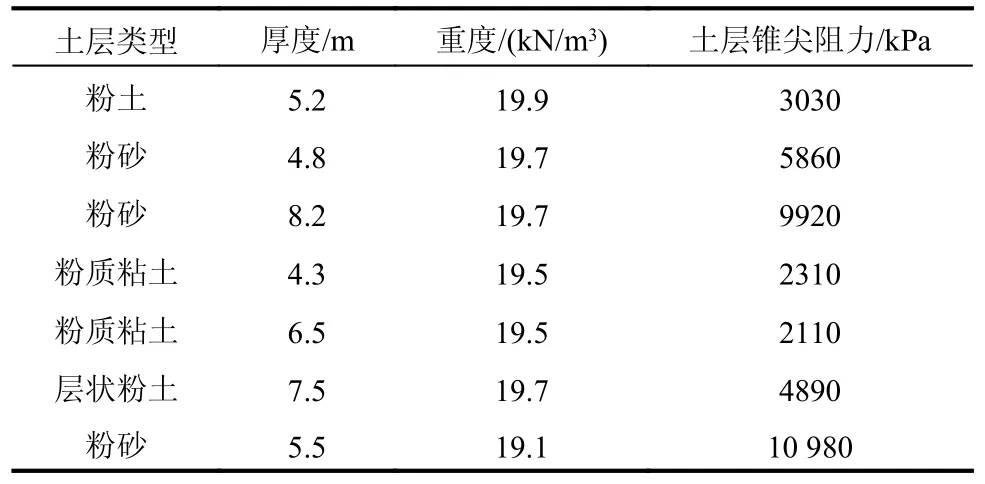
表5 风机基础埋置土层参数[23]Table 5 Parameters of buried soil layer for wind turbine foundation[23]

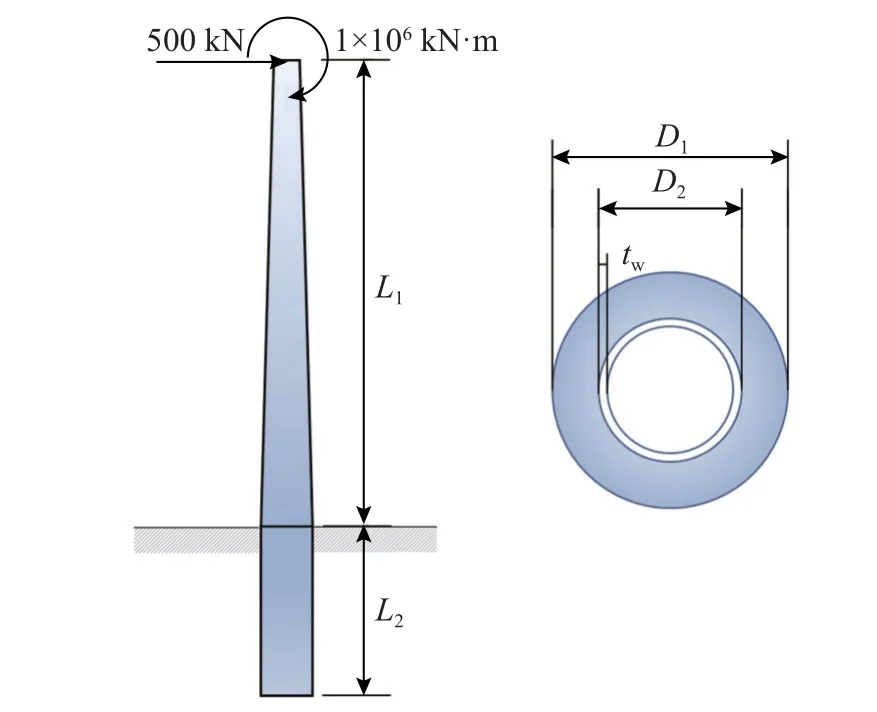
图9 风机支撑结构参数Fig.9 Parameters of wind turbine support structure

图10 实体单元有限元模型示意图Fig.10 Schematic diagram of solid element finite element model

在海洋环境下，风机支撑结构所受的荷载通常包括叶轮气动荷载、塔筒风荷载以及浪流荷载等，其中叶轮气动力一般起控制作用[34]，本节基于常规的风机荷载值进行工况设计。叶轮气动力通常包括水平作用力T与弯矩M，本研究基于莫继华[35]使用叶素-动量理论计算得到的某近海2 MW 叶轮气动力序列(如表6 所示)确定了荷载取值的大致范围。设计了作用于塔筒顶端的500 kN水平荷载工况和500 kN 水平荷载、10 000 kN·m 弯矩组合工况。对模型底部采用两种不同的约束状态，分别为桩底固支和桩底无约束，以分别模拟端承桩与摩擦桩，共计4 种工况。可得四种工况下的桩身变位曲线如图11(a)～图11(d)所示。从图中可知，对于风机单桩支撑结构计算，高性能桩单元的位移计算结果与实体单元趋近于一致，具有很高的精确性和适用性。并且对比两种模型所使用的单元量，使用高性能桩单元对计算资源的消耗量远小于实体单元，这充分体现出了高性能桩单元的高效性。

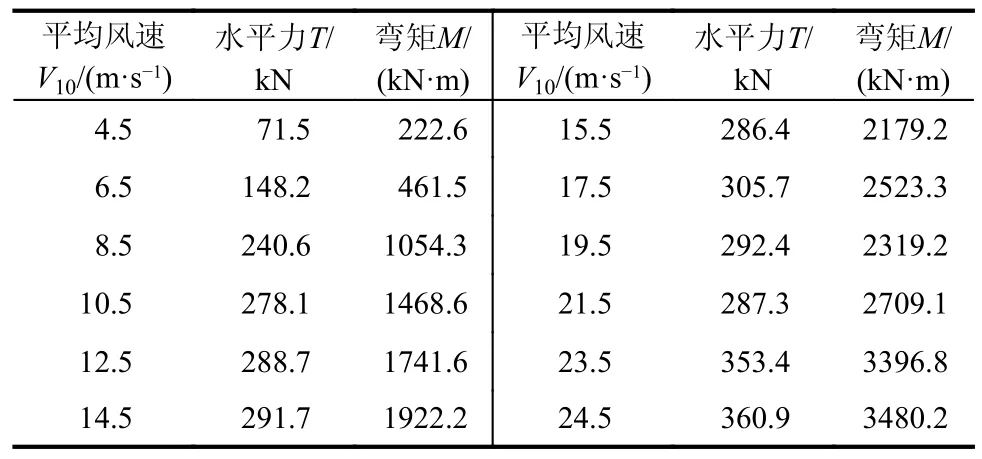
表6 基于叶素-动量理论得到的2 MW 叶轮气动力值[35]Table 6 Aerodynamic value of 2 MW impeller based on blade element momentum theory[35]

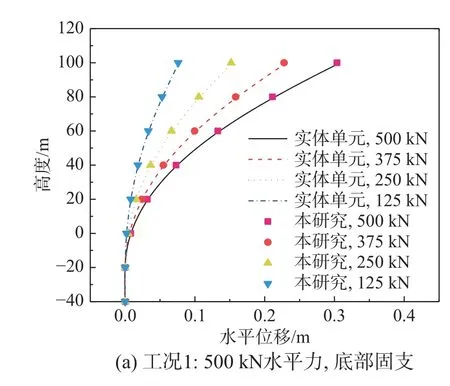
图11 4 种工况下桩体水平变形曲线Fig.11 Horizontal displacement curve of pile under four working conditions

4 大直径单桩水平承载性能参数分析

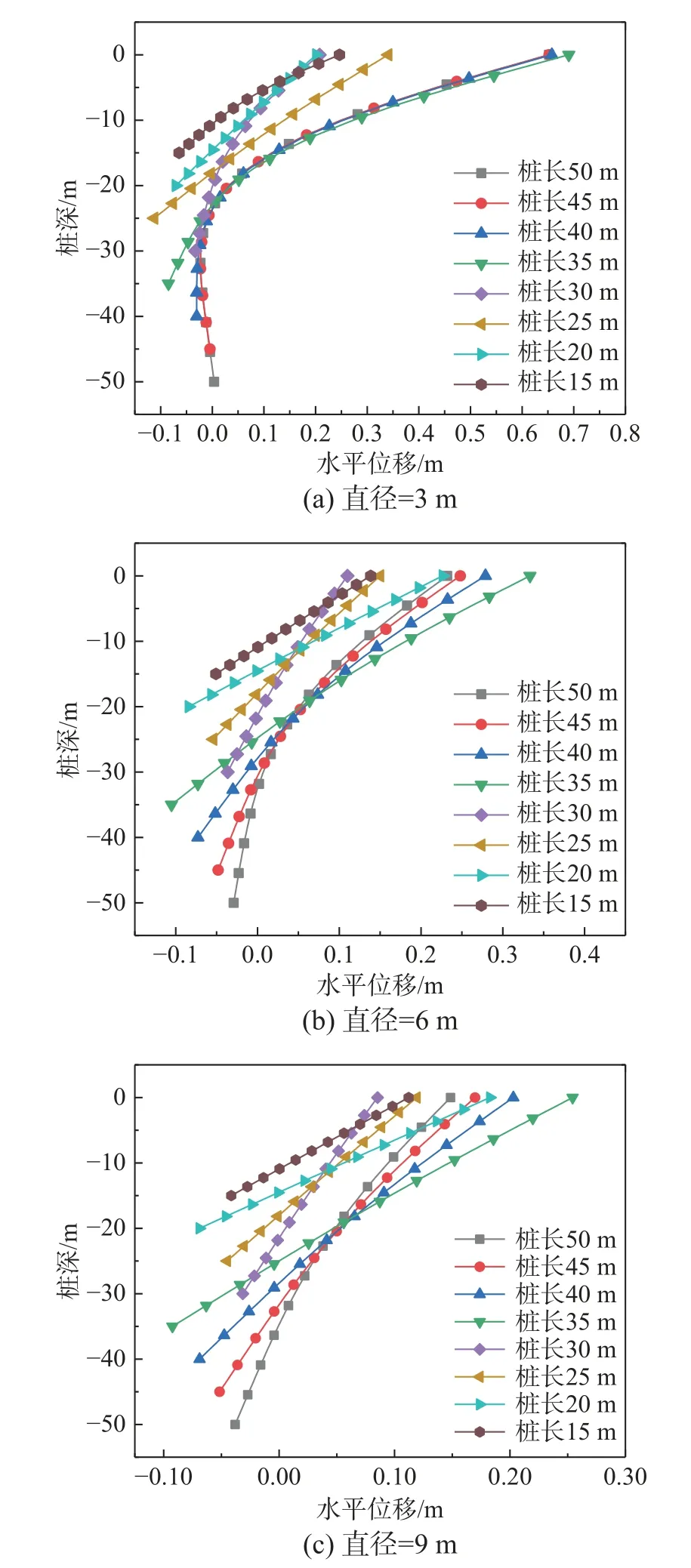
图12 不同桩长、桩径桩水平位移曲线Fig.12 Horizontal displacement curves of piles with different pile lengths and diameters

根据《港口工程桩基规范》(JTS 167-4-2012)[36]，桩基的变形模式可分为：弹性长桩、中长桩和刚性桩，可以根据桩长(L)与桩基相对刚度特征值(T)的大小关系来判断桩基的变形模式，相对刚度特征值通常采用式(18)计算，评判标准如表7 所示：

表7 桩基变形模式评判标准Table 7 Evaluation criteria for pile foundation deformation mode

式中：T为相对刚度特征值；Ep为桩材料的弹性模量；Ip为桩截面的惯性矩；m为桩侧地基土抗力系数随深度增长的系数；b0为桩的换算宽度。

为研究大直径桩变形模式与相对刚度特征值的关系，研究将计算结果根据变形模式进行分类，并计算了各情况下相对刚度特征值与桩长的比值，计算结果如表8 所示，表8 中以深浅两种颜色标记了不同情况下桩的变形模式，两种变形模式的交界位置对应的L/T值可以作为判断两种变形模式的L/T临界值。

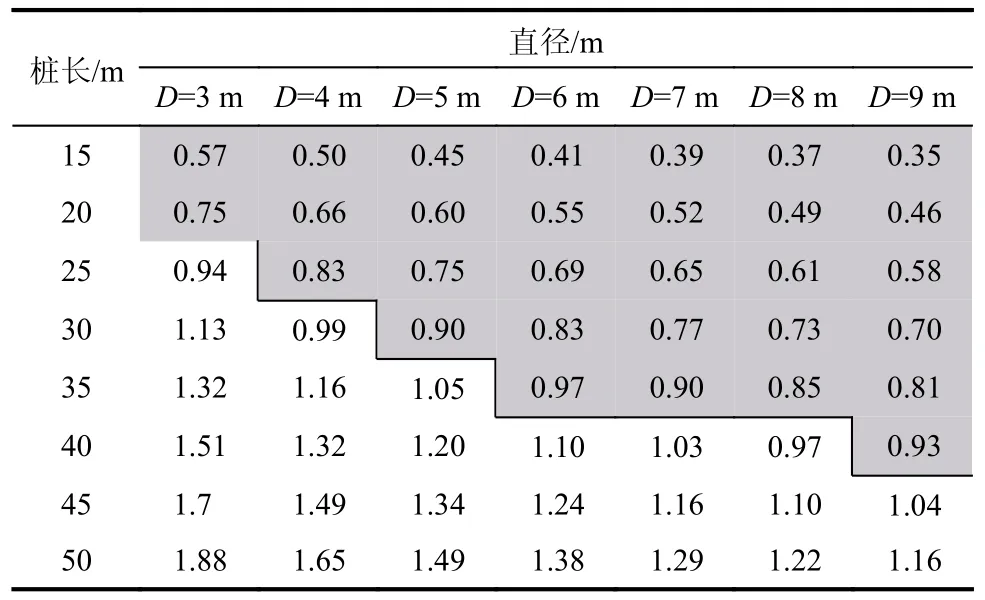
表8 不同参数组合下桩基L/T 值Table 8 L/T value of pile under different parameter combinations

从表8 中可以得到大直径桩的刚性桩-中长桩临界L/T值为0.75～1.10，远远小于规范中规定的2.50，与前人研究中得到的临界L/T值0.8～1.4[37]相较具有良好的一致性。

以桩顶水平位移为20 mm 作为桩基达到正常使用极限状态的标志，计算不同桩长和桩径条件下的桩基水平承载力如图13 所示。从图中可以看到，在给定桩长的条件下，水平承载力随着桩径的增大而近似呈线性增大，这说明直径对桩基水平承载力的影响十分显著，且不只体现在对刚度的增强效应上；在给定桩径的条件下，水平承载力随桩长的变化则呈现显著的非线性。对于小直径桩如3 m 桩，桩长增大时水平承载力增长趋势趋于平缓，桩长达到25 m 后，水平承载力不再受桩长的影响，这说明对于大直径桩，存在水平承载有效桩长问题，在水平荷载下，深部土体所起的水平抗力作用会随桩长增加逐渐减小并趋近于零。本节中，求得3 m、4 m、5 m 桩基直径对应的有效桩长分别约为25 m、35 m、45 m。

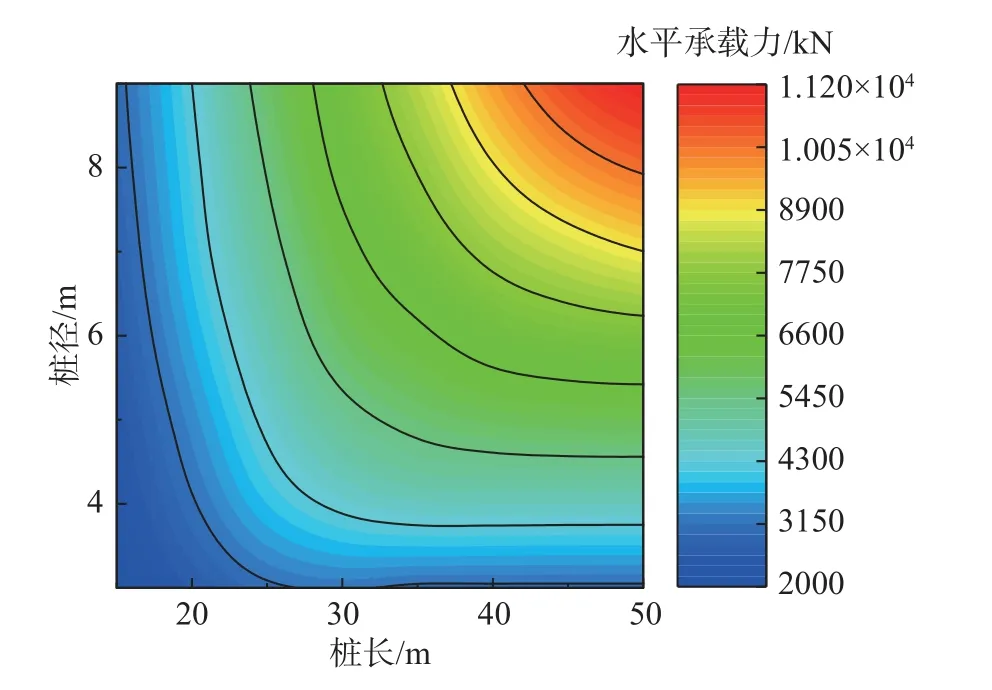
图13 不同桩长-桩径组合桩基水平承载力云图Fig.13 Horizontal bearing capacity of pile with different lengths and diameters

5 结论与建议

本文提出了一种改进的欧拉-伯努利梁单元，以模拟变截面桩在外荷载下的内力与位移响应。本文通过对比传统离散单元法与改进单元法在不同土层中的计算结果和计算资源消耗，验证了改进单元在高度非线性土体中计算的高效性、准确性。在完成验证的基础上，将改进单元应用于海上风电单桩支撑结构的水平承载力研究，得到以下结论：

(1) 在进行海上风机单桩支撑结构计算中，高性能单元法相较于传统梁单元方法具有更高的效率、相当的精确度以及更高的一体化建模程度。计算设置中，只需设置单元本身的参数，而不必对模型进行特殊处理，例如施加节点弹簧、变截面段等效等。基于合适的p-y曲线，高性能桩单元法能进行快速、准确的风机支撑结构一体化计算。

(2) 当前工程界常使用桩长-相对刚度特征值比值判断桩体在水平荷载作用下的变形特性，其中划分刚性短桩-中长桩的规范推荐临界值为2.5，但该值对于大直径桩适用性较差。本文和前人研究中得到该值的范围分别为0.75～1.1 和0.8～1.4，二者具有较好的一致性。

(3) 大直径单桩在水平荷载作用下，随着桩长的增加，其水平承载力增加速率会逐渐减小直至趋近于0，存在有效桩长。实际工程中应当考虑上述效应，确定水平承载有效桩长，以帮助进行合理的单桩尺寸设计。