长周期地震动下大跨空间结构空气弹簧-摩擦摆三维隔震体系振动控制分析

景 铭，韩庆华,2,3，芦 燕,2,3，齐 朋,4

(1.天津大学建筑工程学院，天津 300350；2.中国地震局地震工程综合模拟与城乡抗震韧性重点实验室(天津大学)，天津 300350；3.滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300350；4.中建八局第一建设有限公司，山东，济南 250000)

长周期地震动一般指卓越周期从几秒到十几秒的地震动，分为近断层脉冲型地震动和远场长周期地震动两大类。近断层脉冲型地震动一般产生在距离断层破裂面不超过20 km 的区域内，成因主要与断层破裂的方向性效应和滑冲效应有关[1-3]；远场长周期地震动一般产生在距离震源较远的厚冲击平原或盆地中，由面波激励和场地土放大作用共同引起，成因与地震波的传播路径有关[4-7]。在1994 年的北岭地震(Mw=6.7)[8]、1995 年的阪神地震(Mw=7.2)[9]和1999 年的集集地震(Mw=7.6)[10]中均收集到了大量的长周期地震动记录。

与以高频成分为主的普通地震动不同，长周期地震动因含有丰富的低频成分，易使长周期结构产生更为严重的破坏。在1985 年Michoacan 地震中，墨西哥城下古代湖泊沉积物放大和延长了长周期地震动分量，使距震中400 km 的墨西哥城中约300 座建筑倒塌，800 多座建筑由于无法修复随后被拆除[11]。2008 年汶川地震，距离震中约700 km 的西安市部分高层建筑的剪力墙连梁出现交叉斜裂缝，空心砖填充墙出现开裂，受损严重[12]。此外，距离震中1000 km 以上的苏、沪地区，位于深厚覆盖土层上的高层建筑内人员也有明显的震感，距离震中约1900 km 的台北101 大厦楼内人员也在剧烈晃动中纷纷惊慌逃离。此次震害表明：大震级、远震中距地震对高层建筑的影响比多层建筑大[13]。

已有研究表明：高层建筑结构在长周期地震动作用下将遭受严重的破坏。例如，TAKEWAKI 等[14]以2011 年东日本大地震为背景，分析了长周期地震动作用下40 层和60 层的高层钢结构的地震响应。孙颖等[15]以五跨一联隔震连续梁桥为研究对象，探讨了具有明显脉冲效应的近场、远场长周期地震动作用对采用铅芯橡胶支座(LRB)及摩擦摆隔震支座(FPB)的连续梁桥地震反应。王博等[16]讨论了长周期地震动和长周期结构之间的类共振效应。MAKRIS 和CHANG[17]提出隔震技术对包含长周期脉冲的地震动的有效性。上述研究表明：长周期结构在长周期地震动作用下的响应均大于普通地震动，但上述的研究多集中于高层框架结构，对结构在多类型长周期地震动下响应的对比研究还不够深入和彻底。

大跨空间结构动力特性复杂，其显著的三向振动特性要求其隔震支座必须具有三维隔震能力。针对大跨空间三维隔震体系在长周期地震动下的响应开展深入研究，探究结构在不同类型长周期地震动下的响应特征，提出相应的分析方法具有重要意义。本文将空气弹簧-摩擦摆三维隔震支座应用于大跨单层球面网壳中，分析和探究长周期地震动对三维隔震体系振动控制效果的影响规律。

1 三维隔震体系分析模型

1.1 单层球面网壳模型

本文采用某肋环斜杆型单层球面网壳。网壳跨度142.2 m，矢跨比0.1。钢材为Q355C，采用理想塑性模型，屈服强度为355 MPa。肋环梁采用焊 接H900×(300～500)×(16～18)×(18～25)，斜 杆 为φ(400～550)×10，环梁及人字柱采用φ1000×18 钢管，共684 根杆件。屋面荷载1.3 kN/m2。采用ANSYS 开展有限元分析，径向的肋梁、环向的肋梁和人字形圆钢管支撑柱，采用Beam188 单元模拟；肋环梁之间的斜杆采用Link8 单元模拟。铰支座和隔震支座的位置如图1 所示。

图1 铰支座和三维隔震支座分布位置Fig.1 Layout of hinged bearings and 3D isolation bearings

1.2 三维隔震支座的分析方法

文献[18]提出了一种空气弹簧-摩擦摆三维隔震支座(图2)。该支座中采用空气弹簧为竖向隔震装置，刚度小、频率低，在长周期地震动下可发挥良好的隔震效果。空气弹簧橡胶气囊与上、下端板通过法兰硫化成一体，上、下端板通过螺栓与空气弹簧竖向隔震筒连接在一起。空气弹簧竖向轴承限制了其水平变形，同时起到竖向限位作用。摩擦摆滑块在摩擦摆底座曲面上滑动产生水平位移，依靠重力实现水平自复位，抗拔板实现竖向抗拔和限位。三维隔震支座的水平刚度和竖向刚度完全解耦，因此支座的水平刚度和竖向刚度可以分别设计。

图2 空气弹簧-摩擦摆三维隔震支座Fig.2 Air spring-FPS 3D isolation bearing

1.2.1 水平刚度分析方法

摩擦摆支座可简化成一个沿圆弧面滑道滑动的滑块，如图3 所示。其等效刚度KH-eff、屈服后刚度KH-y和初始刚度KH-p分别为：

图3 摩擦摆分析模型Fig.3 Analytical model of the FPS

式中：RH为滑面曲率半径；D为滑块水平位移；W为上部结构重力；FH为水平回复力；µ为滑面摩擦系数；Dy为摩擦摆的屈服位移。

摩擦摆水平隔震装置力-位移曲线具有双线性特性，如图4 所示，因此在ANSYS 中可用具有双线性特性的Combin40 单元模拟摩擦摆水平隔震装置。

图4 三维隔震支座水平力学模型Fig.4 Mechanical model of the horizontal part of the 3D isolation bearing

由于上部结构的刚度远大于隔震支座，水平隔震装置参数确定应在充分降低上部结构地震响应的基础上，使隔震装置的位移在可接受的范围内。设计时可主要根据目标隔震周期确定摩擦摆隔震装置的水平刚度，带摩擦摆支座结构的水平等效自振周期为[19-20]：

式中：m为上部结构的质量；Te为水平目标隔震周期，仅与滑面曲率半径RH、滑面摩擦系数µ及设计极限位移Dd有关。进行水平隔震设计时应首先确定目标隔震周期，进一步根据式(4)确定滑面的曲率半径、滑面摩擦系数和设计极限位移等参数。为有效消除长周期大跨空间结构高阶振型的影响，目标隔震周期应为原结构自振周期的3 倍以上[20]。

式(4)显示，随着目标隔震周期的延长，水平隔震装置的等效刚度降低，在相同地震动强度下将产生更显著的位移。因此在初步确定支座刚度参数后，应对隔震结构开展动力时程分析，验算其位移响应是否满足设计要求，确保罕遇地震作用下，摩擦摆隔震装置的水平位移小于设计极限位移。

1.2.2 竖向刚度分析方法

空气弹簧是一种利用密封气囊内高压气体的恢复力来实现隔震的非金属弹簧。其竖向承载力F和竖向刚度KV可表示为[18]：

式中：p为空气弹簧囊内气压；Aeff为空气弹簧有效承压面积；α 为气囊竖向形状系数；pa为大气压；V为气体体积。

由于三维隔震支座竖向力-位移曲线具有线性特性[18]，如图5 所示，在ANSYS 中可用具有线性特性的Combin14 单元模拟空气弹簧竖向隔震装置。

图5 三维隔震支座竖向力学模型Fig.5 Mechanical model of the vertical part of the 3D isolation bearing

由于结构的地震响应源于外部激励输入，需将隔震结构的自振频率与输入激励错开。由于隔震层上部结构的水平刚度远大于隔震支座的水平刚度，在地震作用下上部结构变形很小，整体刚体平动，位移集中于隔震层。因此可将隔震结构简化为单自由度体系，其承受的竖向重力荷载和恒荷载可简化为质量块。竖向隔震装置的理论模型如图6 所示。x¨g(t)为输入的简谐激励，即x¨g0sinωt，x¨g0为其加速度峰值。隔震装置的竖向峰值加速度x¨smax可根据式(7)计算[21]。

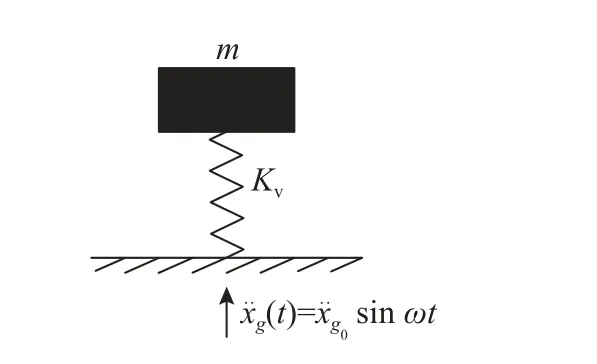
图6 竖向隔震装置的理论模型Fig.6 Theoretical model of vertical isolation device

式中：β 为激励的圆频率ω与支座的竖向自振频率ωn之比；ζ 为支座的阻尼比。定义激励的传递比TR 为隔震装置的竖向峰值加速度x¨smax与输入激励的峰值加速度之比：

激励的传递比TR 仅与支座的阻尼比ζ 和频率比β 有关。输入激励与隔震装置的固有频率之比为隔震装置必须满足的基本条件。当阻尼比较小时，TR 和β 的关系可简化为式(9)：

输入激励的圆频率ω和频率f的关系为：

对于单自由度体系：

式中：FG为支座承受的重力荷载和竖向恒荷载；Δst为支座在自重和恒荷载作用下的竖向静位移。进一步，将式(11)和式(12)代入式(10)，得到：

将式(9)代入式(13)，得：

将式(11)代入式(14)，得：

根据式(15)，给定输入激励时，可根据传递比TR 确定支座的竖向刚度。图7 为激励频率与支座竖向位移关系。当激振频率f恒定时，支座的竖向位移随传递比TR 的降低而增大；当传递比TR 恒定时，支座的竖向位移随激振频率f的降低而增大。

图7 激励频率与支座竖向静位移关系Fig.7 Relationship between the vertical static displacement and excitation frequency

2 长周期地震动特性

本文选择集集地震中5 条近断层脉冲型地震动及5 条远场长周期地震动[15-16]，另选取了5 条不具有长周期脉冲特征的普通地震动记录，见表1。本文选用的地震动数据记录均来自美国太平洋地震工程研究中心数据库网站(PEER)。

表1 所选地震动Table 1 Selected ground motions

由图8 可见，对于近断层脉冲型地震动和远场长周期地震动，其卓越频率主要分布在1 Hz 以下，竖向卓越频率和水平卓越频率接近。对于普通地震动，其卓越频率明显大于上述两种长周期地震动，竖向卓越频率明显大于水平向卓越频率。近断层脉冲型地震动的特性主要体现在峰值和峰值比上，其加速度峰值PGA 和速度峰值PGV均明显大于其他两种地震动，峰值比PGV/PGA 也明显大于普通地震动；远场长周期地震动的特性主要体现在峰值、峰值比和持时上，其峰值加速度PGA 远小于其他两类地震动，峰值比明显大于普通地震动，而持时也明显长于其他两种地震动。研究表明，PGV/PGA≥0.2 表示脉冲特性明显，PGV/PGA<0.2 表示脉冲特性不明显[15]，近断层脉冲型地震动和远场长周期地震动均具有明显的低频脉冲特性，加速度敏感区较宽，而普通地震动不具有脉冲特性。

图8 所选地震动基本特性Fig.8 Basic characteristics of the ground motions

为了解普通地震动和长周期地震动的反应谱特性，图9 绘制了相同PGA 下的加速度反应谱、速度反应谱、位移反应谱，并进行平均化处理，在计算弹性反应谱时将加速度峰值调整至0.4g。两类长周期地震动在中长周期段的各个反应谱值均大于普通地震动，且速度和位移与普通地震动的差异明显大于加速度，与前述长周期地震动低频分量集中的特性相符。相同峰值加速度，远场长周期地震动各反应谱值均大于近断层脉冲型地震动，且衰减更为缓慢。这是由于，远场长周期地震动的持时远长于近断层脉冲型地震动，PGA 相同时，输入能量较大引起的。在4 s～6 s 的长周期段，远场长周期地震动的反应谱具有典型的“双峰”特征，与普通地震动和近断层脉冲型地震动差异明显，两类长周期地震动的各反应谱差值最大，大于6 s 后各反应谱差值迅速减小。由于所选远场长周期地震动的卓越频率主要分布在0.2 Hz 附近，易与自振频率约0.2 Hz 的结构产生共振效应，反应谱峰值出现在5 s 附近。

图9 反应谱对比Fig.9 Comparison of the response spectra

3 三维隔震体系地震响应分析

在自重和恒荷载作用下，单层球面网壳隔震体系支座竖向反力为1660 kN。以TR=0.2 代表刚度较低的空气弹簧竖向隔震装置。由于常见竖向地震动卓越频率范围约7 Hz～20 Hz，根据式(15)，竖向刚度应低于5.3×104kN/m。当三维隔震支座竖向刚度和承载力确定后，可进一步确定空气弹簧的气压和数量等参数。当单个空气弹簧不能满足设计要求时，可采用并联空气弹簧组的构造形式，多组并联的空气弹簧共同受力和变形。在后续分析中摩擦摆滑面曲率半径设为1000 mm，摩擦系数µ设为0.02。节点位置如图10 所示。

图10 节点分布Fig.10 Distribution of nodes

3.1 节点峰值加速度

分别对隔震结构和非隔震结构开展动力时程分析。加速度峰值分别按0.07g和0.4g进行调整，x、y、z向地震动峰值按1∶0.85∶0.65 进行调幅。选取节点峰值加速度和杆件峰值等效应力为振动控制效果评价指标，以隔震率β 为指标进行量化评估。

式中，r0、r分别为非隔震结构或隔震结构的节点峰值加速度或杆件等效应力。

由图11～图13 可见，非隔震结构节点峰值加速度离散性较大，隔震结构节点峰值加速度趋于均匀分布。越靠近网壳中心，节点峰值加速度的隔震率越大。出现放大现象的节点位于第2 环，即V 型柱顶端杆件。在普通地震动和近断层脉冲型地震动作用下，三维隔震支座可有效降低三向节点峰值加速度，但在远场长周期地震动作用下，当PGA 等于0.4g时，y向节点峰值加速度的隔震效果显著降低。普通地震动作用下，水平和竖向节点峰值加速度隔震率分布在40%～60%和60%～80%；近断层脉冲地震动作用下，水平和竖向节点峰值加速度隔震率分布在20%～60%和40%～80%。远场长周期地震动作用下，水平和竖向节点峰值加速度隔震率分布在0%～40%和0%～60%。

图11 普通地震动下平均节点峰值加速度Fig.11 Mean of the nodal peak acceleration under ordinary ground motions

图12 近断层脉冲型地震动下平均节点峰值加速度Fig.12 Mean of the nodal peak acceleration under near-fault pulse-like ground motions

图13 远场长周期地震动下平均节点峰值加速度Fig.13 Mean of the nodal peak acceleration under far-field long-period ground motions

3.2 杆件峰值等效应力

图14 为杆件隔震前后的等效应力。大部分杆件的等效应力均得到了有效控制，隔震后第1 环环向杆和第2 环环向和径向杆出现放大现象。隔震后各个杆件的等效应力趋于均匀分布，由于隔震前这部分杆件的等效应力最小，这部分杆件应力出现放大现象。当PGA=0.07g时，不同的地震动作用下，隔震率分布在0%～20%，小于30%的杆件出现应力放大现象。当PGA=0.4g时，在普通地震动和近断层脉冲地震动作用下，隔震率分布在20%～60%，出现应力放大现象的杆件不足11%，而在远场长周期地震动作用下，有34%的杆件出现了应力放大现象。

图14 不同地震动下平均杆件峰值等效应力Fig.14 Mean of the member peak Mises stress under different ground motions

3.3 隔震支座响应

空气弹簧在标准工作高度的承载力等于自重和恒荷载下的支座反力，空气弹簧仅在地震来临时变形。以普通地震动El Centro、近断层脉冲型地震动TCU068 和远场长周期地震动ILA056 为例，给出三维隔震支座水平位移时程曲线如图15所示。隔震支座的位移时程曲线与地震激励的加速度时程曲线波形一致。近断层脉冲型地震动作用下，支座位移时程曲线具有显著脉冲特性，远场长周期地震动作用下，时程曲线呈现类简谐振动特性，共振效应导致隔震支座在类谐和段产生很大位移反应。

图15 El Centro、TCU068 和ILA056 作用下隔震支座水平位移时程曲线Fig.15 Horizontal displacement time histories of the isolation bearing under El Centro, TCU068, and ILA056 ground motions

表2 列出了所选地震动下支座的峰值位移。相同PGA，对于近断层脉冲型地震动，由于其长周期和脉冲特性，其水平位移和竖向位移分别是普通地震动的1.5 倍～2.6 倍和1.9 倍。对于远场长周期地震动，由于其长周期和类谐和特性，其水平位移和竖向位移分别是普通地震动的1.9 倍～5.8 倍和3.1 倍～3.2 倍。总之，在远场长周期地震动下，支座位移响应最大。

表2 所选地震动下支座峰值位移 /mmTable 2 Peak bearing displacement under the selected ground motions

4 隔震效果影响分析

本节进一步分析了三维隔震支座水平刚度和竖向刚度对单层球面网壳节点峰值加速度、杆件等效应力和支座位移响应的影响规律。

4.1 支座水平刚度对隔震效果的影响分析

当支座承受的竖向荷载不变时，摩擦摆的水平刚度仅与滑面曲率半径R和滑面摩擦系数µ有关。本节以滑面曲率半径R和滑面摩擦系数µ为变量，探究隔震支座水平刚度对隔震效果的影响。本节中TR 取0.2，保持竖向刚度不变。滑面摩擦系数µ与接触面材料种类以及是否润滑有关，取滑面摩擦系数µ介于0.01～0.1，滑面曲率半径R取1.0 m、1.5 m 和2.0 m。三维隔震支座的水平刚度见表3。

表3 三维隔震支座水平刚度 /(kN/m)Table 3 Horizontal stiffness of the 3D isolation bearing

支座水平刚度对单层球面网壳动力响应的影响如图16～图18 所示。在普通地震动El Centro 和近断层脉冲型地震动TCU068 作用下，随着滑面摩擦系数µ的减小与滑面曲率半径R的增大，节点水平峰值加速度减小，隔震效果提高。在远场长周期地震动ILA056 作用下，随着滑面摩擦系数µ的减小和滑面曲率半径R的增大，节点水平峰值加速度增大，隔震效果降低。

图16 滑面摩擦系数µ与滑面曲率半径R 对节点峰值加速度的影响Fig.16 Influence of friction coefficient of the sliding surface µ and radius of the sliding surface R on the nodal peak acceleration

图17 滑面摩擦系数µ与滑面曲率半径R 对杆件峰值等效应力的影响Fig.17 Influence of friction coefficient of the sliding surface µ and radius of the sliding surface R on the member peak Mises stress

图18 滑面摩擦系数µ与滑面曲率半径R 对支座位移响应的影响Fig.18 Influence of friction coefficient of the sliding surface µ and radius of the sliding surface R on the bearing displacement

改变支座的水平刚度对节点竖向峰值加速度也有一定的影响。对于普通地震动El Centro 和近断层脉冲型地震动TCU068，节点竖向峰值加速度随着滑面摩擦系数µ的减小而减小，对于远场长周期地震动ILA056 则相反。滑面曲率半径R对竖向节点峰值加速度基本无影响。

杆件峰值等效应力在不同地震动作用下随滑面摩擦系数µ与滑面曲率半径R的变化规律与节点峰值加速度类似。当PGA=0.07g时，不同滑面曲率半径R对应的杆件峰值等效应力基本相等；当PGA=0.4g时，滑面曲率半径R对杆件峰值等效应力的影响更为显著，尤其是近断层脉冲型地震动和远场长周期地震动。

支座三向位移均随PGA 的增大而增大。当地震动强度较大时(PGA=0.4g)，支座位移响应受滑面摩擦系数µ与滑面曲率半径R的影响很大。随着滑面摩擦系数µ的减小与滑面曲率半径R的增大，支座水平位移增大。滑面摩擦系数µ对支座水平位移的影响，大于对滑面曲率半径R的影响。

改变支座水平刚度对支座竖向位移响应影响较小。在普通地震动El Centro 和近断层脉冲型地震动TCU068 作用下，随着滑面摩擦系数µ的减小与滑面曲率半径R的增大，支座竖向位移响应减小；远场长周期地震动ILA056 作用下则相反。

图19 为水平加速度反应谱及当R=2.0 m 时的结构水平自振周期。随着摩擦系数µ的减小，支座、水平刚度减小，结构水平自振周期延长。对于普通地震动El Centro 和近断层脉冲型地震动TCU068，加速度反应谱值随结构周期的延长而减小，隔震效果提高。对于远场长周期地震动ILA056，其丰富的长周期低频分量导致其反应谱值衰减最慢，甚至具有“双峰”特性，导致在远场长周期地震动作用下，隔震效果随结构自振周期的延长而降低。

图19 水平加速度反应谱及不同µ对应的结构水平自振周期Fig.19 Horizontal acceleration response spectra and the values for the structural horizontal period corresponding to different µ

4.2 支座竖向刚度对隔震效果的影响

TR 与支座的竖向刚度直接相关，支座竖向刚度随TR 的增大而增大。在本节分析中，滑面摩擦系数µ取0.02，滑面曲率半径R取1 m，保持水平刚度不变。TR 的取值范围为0.05～0.9，以TR=1代表水平隔震支座。三维隔震支座的竖向刚度见表4。支座竖向刚度对单层球面网壳动力响应的影响规律如图20～图22 所示。改变支座竖向刚度，对水平节点峰值加速度基本无影响。对于普通地震动El Centro 和近断层脉冲型地震动TCU068，节点竖向峰值加速度和杆件峰值等效应力随竖向刚度的降低而降低，隔震效果提高；但对于远场长周期地震动ILA056，则相反(图20、图21)。改变支座竖向刚度对支座水平x和y向的位移响应基本无影响。随着TR 的增大，即支座竖向刚度的增大，支座竖向位移响应减小。当TR=0.2～0.9 时，支座竖向位移变化平缓，当 TR ＜0.2时，随着TR 的增大，支座竖向位移迅速降低(见图22)。

表4 三维隔震支座竖向刚度 /(kN·m-1)Table 4 Vertical stiffness of the 3D isolation bearing

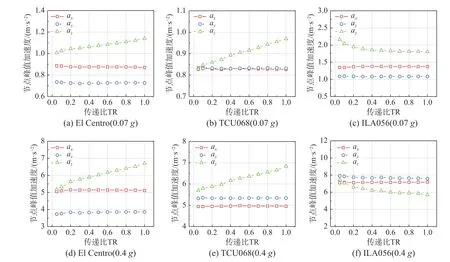
图20 TR 对节点峰值加速度的影响Fig.20 Influence of TR on the nodal peak acceleration

图21 TR 对杆件峰值等效应力的影响Fig.21 Influence of TR on the member peak Mises stress

图22 TR 对支座位移响应的影响Fig.22 Influence of TR on the bearing displacement

降低支座的竖向刚度，可有效提高普通地震动和近断层脉冲型地震动作用下的隔震效果，但对于远场长周期地震动，虽然出现了隔震效果随竖向刚度降低而降低的现象，但该现象仅在TR ＜0.2时较为明显。该现象依然与远场长周期地震动低频分量丰富的特性有关。图23 为不同地震动竖向分量的加速度反应谱及结构竖向自振周期。对于普通地震动El Centro 和近断层脉冲型地震动TCU068，加速度谱值随着周期的延长而缓慢降低，但对于远场长周期地震动ILA056，其明显的“双峰”特性导致加速度谱值在1.5 s 后出现随周期延长而增加的现象。总之，选取TR=0.2 的竖向隔震装置不仅可有效降低普通地震动和近断层脉冲型地震动作用下的结构响应，对远场长周期地震动作用下的结构响应也有一定的控制作用，且支座的位移响应均在竖向行程之内。

图23 竖向加速度反应谱以及不同TR 对应的结构竖向自振周期Fig.23 Vertical acceleration response spectra and the values for the structural vertical period corresponding to different TR

5 结论

本文以单层球面网壳为研究对象，探究了长周期地震动对空气弹簧-摩擦摆三维隔震体系的隔震效果，得到以下结论：

(1) 本文提出了空气弹簧-摩擦摆三维隔震支座在大跨空间结构中的分析方法。摩擦摆水平隔震装置的刚度可由目标水平隔震周期确定，空气弹簧竖向隔震装置的刚度可由激励的传递比TR 和输入激励的卓越频率确定。

(2) 在普通地震动和长周期地震动作用下，三维隔震支座均可有效降低网壳的节点加速度和杆件等效应力。相同PGA，普通地震动作用下的隔震效果最优，近断层脉冲型地震动作用下隔震效果次之，远场长周期地震动作用下隔震效果最差。普通地震动下的支座位移响应最小，近断层脉冲地震动次之，远场长周期地震动支座位移响应最大。长周期地震动中丰富的低频分量与长周期隔震结构的类共振效应是隔震效果降低的原因。

(3) 随着支座水平和竖向刚度的减小，普通地震动和近断层脉冲型地震动作用下隔震效果提高，远场长周期地震动作用下隔震效果降低。远场长周期地震动丰富的低频特性使其反应谱具有“双峰”特性，导致结构响应在长周期段出现随周期的延长而增大的现象。TR 建议取值应大于0.2，既保证隔震效果，又能控制三维隔震支座竖向位移响应在设计极限位移内。