抗泄漏CCA 安全的内积功能加密*

韩 帅，刘胜利，3，谷大武

1.上海交通大学 电子信息与电气工程学院，上海200240

2.密码科学技术全国重点实验室，北京100878

3.成都卫士通信息产业股份有限公司 摩石实验室，北京100070

1 引言

功能加密(functional encryption，FE)[1-3]是一种灵活的加密模式，由Boneh 等人于2011 年[1]首次提出并给出正式定义.通过对传统加密的推广和扩展，功能加密支持密文上的精细化访问控制.传统的加密方案如公钥加密方案(public-key encryption，PKE) 提供了“全有或全无” 的访问控制，仅私钥sk 的持有者能够从密文中解密恢复出明文消息，而其他任何人都不能从密文中获得关于明文的任何信息.而功能加密提供了更为精细的访问控制.具体而言，功能加密的访问控制能力由一个函数族F所刻画.私钥sk 的持有者可以为函数族F中的任一函数生成一个功能密钥skf.持有功能密钥skf者对一个加密消息x的密文ct 进行解密，仅能获得函数值f(x)，而对x的其它信息一无所知.

一般而言，根据支持的函数族F，功能加密可以分为两类.第一类功能加密可以支持所有多项式时间可计算的函数[4-7].虽然这类功能加密支持的函数族非常大，但是其构造往往非常复杂，需要使用不可区分混淆[6]、多线性映射[8]等很强的密码工具.因此，这类功能加密难以实际应用在现实场景中.第二类功能加密仅支持一些特殊的函数族，如内积函数族[9-14]、二次函数族[15-19]等.这类功能加密往往构造较为高效，无需使用不可区分混淆、多线性映射等复杂密码工具，更适合应用于现实场景中.虽然这类功能加密支持的函数族比较有限，但是在很多实际场景中都能够满足应用需求.

本文将主要研究支持内积函数族的功能加密，简记为内积功能加密(inner-product FE，IPFE).具体而言，内积功能加密所加密的消息为一个向量Zm，所生成的功能密钥也与一个向量Zm相关.使用向量y对应的功能密钥sky来对向量x的密文ct 进行解密可以得到内积值〈x，y〉Z.实际上，内积功能加密可以满足许多实际场景的应用需求，例如用来计算明文数据的析取、合取、加权平均值等多种统计信息，适用于生物特征认证、近邻搜索和统计分析等多种应用场景[9，20，21].

内积功能加密的安全性.内积功能加密的常规安全性要求为选择明文/密文攻击下的不可区分性(indistinguishability under chosen-plaintext/ciphertext attacks，IND-CPA/CCA).IND-CPA 安全性要求概率多项式时间的敌手A无法区分向量x0的密文和向量x1的密文，即使A可以通过功能密钥查询获得许多功能密钥: 每一次查询时，A提交一个向量y，并获得对应的功能密钥sky.为了防止平凡攻击，我们要求A仅能获得满足〈x0，y〉〈x1，y〉 的向量y所对应的功能密钥.这里的向量x0、x1以及A进行功能密钥查询的向量y都可以由敌手A适应性地选择.IND-CCA 安全性比IND-CPA 更强，还允许敌手A进行解密查询: 每一次查询时，A提交一个向量y和一个密文ct，并获得使用功能密钥sky对ct进行解密的结果.

2016 年，Agrawal 等人[10]分别基于标准的DDH(decisional Diffie-Hellman)、LWE(learning-witherrors) 和DCR (decisional composite residuosity) 假设，给出了多个满足IND-CPA 安全性的内积功能加密方案.同年，Zhang 等人[22]基于DDH 假设构造了首个IND-CCA 安全的内积功能加密方案.随后，Benhamouda 等人[11]基于DCR 假设也得到了IND-CCA 安全的内积功能加密方案.此外，Tomida[12]和Liu 等人[13，14]还分别给出了具有紧致安全规约的IND-CPA 和IND-CCA 安全性的内积功能加密方案.

抗泄漏安全性.IND-CPA 和IND-CCA 安全性中实际上隐含一个非常理想的假设，即假设密钥sk对于敌手A而言是完全保密的.而在实际的密码学应用中，密码方案还面临着密钥泄漏等安全威胁.通过使用侧信道攻击技术[23-25]，敌手可以对密码设备运行时的功耗、时间、电磁辐射、微波等信息进行分析，进而获得密钥sk 的部分信息.在安全模型中，通常用密钥泄漏查询来刻画这一攻击能力: 每一次查询时，A可以提交一个函数L，并获得由函数L指定的密钥信息L(sk).抗泄漏(leakage-resilient，LR) 安全性要求对于能够进行密钥泄漏查询的敌手A，密码方案仍然是安全的.具体而言，抗泄漏CPA/CCA 安全性要求IND-CPA/CCA 安全性在敌手A能够进行密钥泄漏查询时仍然成立.本文，我们将主要考虑有界泄漏模型[26，27]，即要求敌手通过泄漏查询获得的密钥总泄漏比特数|L(sk)| 小于密钥的总比特数|sk|.特别地，抗泄漏安全性所容许的最大泄漏比特数|L(sk)| 与密钥比特数|sk| 之间的比值|L(sk)|/|sk| 称为泄漏率(leakage rate).

目前，抗泄漏安全性的研究主要集中在传统的公钥加密方案[26-29]、基于身份加密方案[30-37]、基于属性加密方案[31，37-39]等，而关于功能加密的研究工作相对较少[40-45].下面对已有的抗泄漏安全功能加密的相关工作进行介绍.1在功能加密的抗泄漏安全性相关工作中，部分工作[40–42] 所研究的功能加密与Boneh 等人于2011 年[1] 提出的功能加密(也即本文所考虑的功能加密) 不同，它们所考虑的功能加密仍然是一种“全有或全无” 的密文访问控制: 在加密时除了输入明文消息x 还会输入一个元素a;而使用功能密钥skf 解密时，要么在f(a)=1 时恢复出整个明文x，要么在f(a)=0 时无法获得明文的任何信息.因此，这里未对这些工作进行详细介绍.

— 2018 年，Wang 等人[43]正式为功能加密定义了抗泄漏安全性，并基于混淆电路技术构造了抗泄漏CCA 安全的功能加密方案.该方案的抗泄漏CCA 安全性可以基于DDH 假设或者DCR 假设，且支持的泄漏率达到了-o(1).但是该工作中考虑的抗泄漏CCA 安全性较弱: 其允许敌手获得私钥sk 的泄漏信息，但仅允许敌手A进行1 次功能密钥查询(即仅能获得1 个功能密钥skf)，且敌手A需要在游戏一开始就提交消息x0，x1以及要进行功能密钥查询的函数f(因此不是适应性的).此外，虽然该功能加密方案可以支持所有多项式时间可计算的函数，但是由于使用了混淆电路的技术，构造较为复杂.

— 2020 年，Zhang 等人[44，45]研究了内积功能加密的抗泄漏安全性，并基于抗泄漏的内积哈希证明系统技术构造了抗泄漏CPA 安全的内积功能加密方案.该方案基于DDH 假设，且在内积函数的向量维数为m时，支持的泄漏率为-o(1).该工作中考虑的抗泄漏CPA 安全性也相对较弱:

其不允许敌手A获得(主) 私钥sk 的泄漏信息，仅允许敌手获得功能密钥sky的泄漏信息.目前已有的功能加密方案达到的抗泄漏安全性较弱，如何构造具有较强抗泄漏安全性的功能加密方案仍然是一个尚未解决的问题.

本文贡献.在本文中，我们设计了第一个达到适应性抗泄漏CCA 安全性的内积功能加密方案.

· 首先，给出了本文所考虑的抗泄漏CCA 安全性的正式定义.我们考虑的抗泄漏CCA 安全性是适应性的，允许敌手A适应性地进行下面四种查询: 进行(主) 私钥sk 的泄漏查询、功能密钥sky的泄漏查询、功能密钥sky的查询以及解密查询.2为了防止平凡攻击，要求A 仅能对满足〈x0，y〉= 〈x1，y〉 条件的向量y 进行功能密钥查询.但我们对功能密钥sky 泄漏查询的向量y 没有这一要求.因此敌手A 可以对满足上述条件的y 进行功能密钥查询，而对不满足上述条件的y 仍然可以进行功能密钥的泄漏查询.这是为什么本文的安全模型同时允许敌手进行功能密钥泄漏查询和功能密钥查询的原因.关于本文安全模型的更多解释和说明请参见第3 节中的注1.其正式定义请参见第3 节.因此，我们考虑的抗泄漏CCA 安全性比已有工作中考虑的功能加密抗泄漏安全性[43-45]都要强.

· 然后，基于非对称配对群构造了一个内积功能加密方案，并在标准模型以及标准的MDDH (matrix decisional Diffie-Hellman) 假设[46]下证明了本文方案满足上述较强的抗泄漏CCA 安全性.MDDH 假设包含了标准的DDH 假设和k-Linear(k-LIN) 假设[46]，因此通过我们的构造实际上可以分别得到基于DDH 假设和k-LIN 假设的抗泄漏CCA 安全内积功能加密方案.本文方案是第一个达到适应性抗泄漏CCA 安全的内积功能加密方案.方案的具体构造及其抗泄漏CCA 安全性证明请参见第4 节.

表1 中将本文构造的内积功能加密方案所达到的抗泄漏CCA 安全性与已有工作[43-45]进行了对比，其中“✓” 表示具有该性质，“×” 表示不具有该性质，“—” 表示未考虑该性质，“(···)” 中标明了方案所支持的泄漏率，“m” 为内积函数的向量维数.

表1 抗泄漏安全功能加密方案的抗泄漏安全性比较Table 1 Leakage-resilient security comparison of leakage-resilient secure FE schemes

2 预备知识

本节将介绍文中使用的符号和基本工具，然后给出内积功能加密及MDDH 假设的定义.

2.1 符号说明和基本工具

首先对所使用的符号进行说明.N 表示自然数集合，Z 表示整数集合.本文统一用N 表示安全参数，并且默认所有的算法、概率分布、函数以及敌手都会将1λ作为一个隐含的输入.本文中的所有算法如无特殊说明都是概率算法.对于集合X，x ←$X表示从集合X中均匀选取元素x.对于概率分布D，x ←$D表示按照概率分布D选取元素x.对于算法A，y ←$A(x) 表示算法A以x作为输入时的运行结果为y.如果A是确定性算法，将其记作y ←A(x).“PPT” 为概率多项式时间(probabilistic polynomial-time) 的简记.poly 表示多项式函数，negl 表示可忽略函数.

本文中的所有向量如无特殊说明都是列向量.对于向量x，x⊤表示它的转置，‖x‖∞表示它的无穷范数，即x的所有分量中绝对值的最大值.

对于两个向量x，Zm，〈x，y〉 表示它们的内积x⊤yZ.

对于随机变量X和Y，X的最小熵定义为H∞(X) :-log(maxxPr[Xx])，X和Y的统计距离定义为Δ(X，Y):

定义 1(抗碰撞哈希函数) 一个哈希函数族H是抗碰撞的，如果对于任意PPT 敌手A，满足:Pr[H ←$H，(x1，x2)←$A(H):x1/x2∧H(x1)H(x2)]≤negl(λ).

2.2 内积功能加密

下面给出内积功能加密的语义以及正确性要求.与文献[10，12] 等工作一样，我们考虑的内积函数〈x，y〉 为多项式有界的，即要求‖x‖∞≤X，‖y‖∞≤Y，其中上界X和Y为关于安全参数λ的多项式.

定义2(内积功能加密) 令Xpoly(λ) 和Ypoly(λ) 为内积函数的多项式上界.一个内积功能加密方案IPFE(Par，Setup，KGen，Enc，Dec) 由如下五个PPT 算法组成:

· pp←$Par: 参数生成算法Par 生成一个公开系统参数pp.为了方便起见，pp 会默认作为所有其他算法的一个输入.

· (mpk，msk)←$Setup(1m): 设置算法Setup 输入内积函数的向量维数N，生成一对主公钥/主私钥(mpk，msk).为了方便起见，mpk 会默认作为KGen 和Dec 算法的一个输入.

· sky ←$KGen(msk，y): 密钥生成算法KGen 输入主私钥msk 和一个向量Zm，生成一个功能密钥sky.

· ct←$Enc(mpk，x): 加密算法Enc 输入主公钥mpk 和一个向量Zm，生成一个密文ct.

·d/⊥←Dec(sky，ct): 解密算法Dec 输入一个功能密钥sky和一个密文ct，输出一个解密结果Z 或者一个代表解密失败的特殊符号⊥.

正确性要求: 对所有的N，x，Zm，‖x‖∞≤X，‖y‖∞≤Y，pp←$Par，(mpk，msk)←$Setup(1m)，sky ←$KGen(msk，y) 和ct←$Enc(mpk，x)，都一定有Dec(sky，ct)〈x，y〉 成立.

接下来给出内积功能加密的选择明文/密文攻击下的不可区分性(indistinguishability under chosenplaintext/ciphertext attacks，IND-CPA/CCA) 定义.

如果不允许敌手A在图1 中描述的实验进行ODEC查询，则称IPFE 是IND-CPA 安全的.

图1 内积功能加密IPFE 的IND-CCA 安全实验Figure 1 IND-CCA security experiment for IPFE

2.3 MDDH 假设

令l，N 且满足l ＞k.我们称一个概率分布Dl，k为矩阵分布，如果它的输出都是上的满秩矩阵.不失一般性，假设A ←$Dl，k的前k行线性无关.一个特殊的矩阵分布为均匀矩阵分布Ul，k，其输出为上的均匀矩阵.如果lk+1，则记Dk:Dk+1，k，Uk:Uk+1，k.

下面回顾MDDH (matrix decisional Diffie-Hellman) 假设.

MDDH 假设包括了许多标准假设.例如通过将矩阵分布Dl，k实例化为如下的LIN1 和LIN k:

得到的LIN1-MDDH 假设和LIN k-MDDH 假设实际上分别就是标准的DDH 假设和k-Linear(k-LIN)假设[46].MDDH 假设还包括了标准的SXDH (symmetric external DH) 假设，即要求DDH 假设同时在群G1和群G2上成立.

Dl，k-MDDH 假设与均匀矩阵分布的Ul，k-MDDH 假设之间有密切的关系，下面回顾文献[46，49] 中建立的结论.

KerMDH(Kernel Matrix DH) 假设[50]是MDDH 假设的一个计算版本，下面回顾其定义.

下面的引理表明Dl，k-MDDH 假设比Dl，k-KerMDH 假设更强，因为我们可以很容易用满足x⊤A0的非零向量[x]3-s来高效地判断一个向量[u]s是否在span([A]s) 中.

3 内积功能加密的抗泄漏安全性

本节给出内积功能加密的抗泄漏安全性定义，包括抗泄漏CPA 和抗泄漏CCA (leakage-resilience under chosen plaintext/ciphertext attacks，LR-CPA/CCA) 两种安全性定义.

定义6(抗泄漏CPA/CCA 安全性) 令N 表示容许的泄漏比特数.一个内积功能加密方案IPFE(Par，Setup，KGen，Enc，Dec) 是κ-LR-CCA 安全的，如果对于任意PPT 敌手A，满足

显然，当κ0 时，κ-LR-CPA/CCA 安全性就退化为定义3 中的IND-CPA/CCA 安全性.下面对抗泄漏CPA/CCA 安全性的形式化进行说明.

注1(关于抗泄漏CPA/CCA 安全性的形式化) 在图2 描述的实验中，敌手A可以适应性地进行四种查询:

图2 内积功能加密IPFE 的LR-CCA 安全实验，其中|·| 代表比特长度Figure 2 LR-CCA security experiment for IPFE，where |·| denotes bit-length

— 通过功能密钥查询OKGEN(y)，A可以获得功能密钥sky;

— 通过解密查询ODEC(y，ct)，A可以获得ct 在功能密钥sky下的解密结果;

— 通过功能密钥泄漏查询OLEAK(y，L)，A可以获得关于功能密钥sky的部分泄漏信息L(sky);

— 通过主私钥泄漏查询OMLEAK(L)，A可以获得关于主私钥msk 的部分泄漏信息L(msk).特别地，最后两种查询OLEAK和OMLEAK是与图1 中描述的IND-CCA 安全实验相比新增的地方，刻画了A的泄漏攻击能力.由于本文考虑有界泄漏模型[26，27]，因此我们要求A通过OLEAK和OMLEAK获得的密钥总泄漏量不超过κ比特，这由图2 中的变量ℓ及相关判断条件所刻画.此外，A可以在整个实验过程中适应性地提交一对挑战向量(x0，x1)，并获得xβ的加密结果ct*作为挑战密文，其中β为A需要猜测的挑战比特.因此，我们定义的抗泄漏CPA/CCA 安全性是完全适应性的.

为了防止平凡攻击，我们对敌手A的查询有如下限制:

·A进行的所有OKGEN(y) 查询必须满足〈x0，y〉〈x1，y〉;否则A可以使用sky对挑战密文ct*进行解密，计算出〈xβ，y〉，进而成功恢复出β.

·A不能对挑战密文ct*进行ODEC查询;否则A很容易通过解密结果知道β的值.上面两个限制条件与图1 中描述的IND-CCA 安全实验中一样.此外，对于敌手A的OLEAK和OMLEAK查询，我们有如下限制:

·A不能在收到挑战密文ct*之后继续进行OLEAK和OMLEAK查询;否则A很容易通过OLEAK或OMLEAK查询获得β的值.具体而言，A在收到挑战密文ct*后，可以选择一个满足〈x0，y〉/〈x1，y〉 的向量y，定义一个以功能密钥sky为输入、输出仅为1 比特的特殊函数L:

然后进行一次OLEAK查询(y，L)，就可以通过1 比特泄漏信息L(sky) 知道β的值.类似地，A也可以定义一个以主私钥msk 为输入、输出仅为1 比特的特殊函数L:

然后进行一次OMLEAK查询(L)，就可以通过1 比特泄漏信息L(msk) 知道β的值.

该限制条件与已有的公钥加密方案的抗泄漏安全性定义[26，27]以及内积功能加密方案的抗泄漏安全性定义[44，45]类似，均不允许敌手在获得挑战密文之后继续获得关于密钥的泄漏信息.

4 抗泄漏CCA 安全的内积功能加密方案与安全性证明

本节将基于非对称配对群构造一个抗泄漏CCA 安全的内积功能加密方案，并在标准模型和标准的MDDH 假设下证明其抗泄漏CCA 安全性.本文方案是第一个达到适应性抗泄漏CCA 安全性的内积功能加密方案.

具体而言，4.1 节将给出内积功能加密方案的具体构造，4.2 节给出其基于MDDH 假设的抗泄漏CCA安全性证明.

4.1 内积功能加密方案构造

令PGGen 为非对称配对群的生成算法.令Dk和U(m+k+2)，k为两个矩阵分布，其中N 为MDDH 假设的参数，N 为内积函数的向量维数.令H是一族从{0，1}*到Zp的抗碰撞哈希函数.令Xpoly(λ) 和Ypoly(λ) 为内积函数的多项式上界.图3 中给出内积功能加密方案IPFE(Par，Setup，KGen，Enc，Dec) 的具体构造.

图3 基于MDDH 假设构造的内积功能加密方案IPFE=(Par，Setup，KGen，Enc，Dec)Figure 3 Construction of scheme IPFE=(Par，Setup，KGen，Enc，Dec) based on MDDH

首先说明构造的内积功能加密方案IPFE 满足正确性要求.对于任意向量Zm的密文ct([c]1，[d]1，[e]1)，我们有[c]1:[A]1s，[d]1:[W A]1s+[x]1以及[e]1:[(K0+τK1)A]1s，因此可以得到

故能够通过解密算法Dec 的验证.进一步，对于任意向量Zm，使用其功能密钥sky(-y⊤W，y) 对ct 进行解密，可以得到

因此对于多项式有界的‖x‖∞≤X和‖y‖∞≤Y，解密算法Dec 可以在[-mXY，mXY] 范围内求解出离散对数dy⊤x，进而成功计算出内积值y⊤x〈x，y〉.

从技术层面来说，本文的内积功能加密方案IPFE 可以看成是有机结合和改造了Agrawal 等人提出的IND-CPA 安全的内积功能加密方案[10](这对应于我们密文ct 中的[c]1和[d]1) 以及Kiltz 和Wee提出的具有一次模拟健壮性(one-time simulation-soundness) 的非交互零知识证明系统[51](这对应于我们密文ct 中的[e]1，其本质上是在证明[c]1属于线性空间span([A]1)).但是我们强调，Agrawal 等人的方案以及Kiltz 和Wee 提出的系统均未考虑密钥泄漏.为了实现适应性的抗泄漏CCA 安全性，我们将他们的技术在密钥泄漏场景下进行了改造.此外，我们密文ct 中的[c]1和[d]1部分与文献[10] 中的方案仅仅是结构类似，而维数却非常不同.为了能够证明适应性的抗泄漏安全性，我们将文献[10] 中IND-CPA安全内积功能加密方案的密文中2 维的[c]1扩展到了m+k+2 维的[c]1，这使得我们可以借助统计性的复杂性杠杆(complexity leveraging) 技术[52]来证明适应性安全性(即允许敌手A在整个实验过程中的任意时刻提交挑战向量(x0，x1)).相应地，我们将文献[51] 的非交互零知识证明系统进行了调整，使其能够证明更高维数的[c]1.一方面，密文ct 中的[e]1部分可以帮助我们在解密时拒绝一些由敌手“非法” 生成的密文，从而实现CCA 安全性.另一方面，由于[e]1的生成过程[e]1[(K0+τK1)A]1s以及[e]1的验证过程e([c⊤]1，[(+)B]2)e([e⊤]1，[B]2) 都是可以公开计算的，即仅需要使用公开的pp 和mpk，因此[e]1的生成和验证不会在主私钥msk 和功能密钥sky中引入更多元素，这帮助我们最终能够在保持抗泄漏安全性的同时实现CCA 安全性.

4.2 节将基于Dk-MDDH 假设证明本文的内积功能加密方案IPFE 是κ-LR-CCA 安全的，其中容许的泄漏比特数κ ≤logp-2λ.这里，我们对IPFE 方案的效率和泄漏率进行分析.令x·G 表示群G中的x个元素.当MDDH 参数为k、内积函数的向量维数为m时，IPFE 方案的公开系统参数pp 包含(k2+k)·G2，主公钥mpk 包含(2mk+3k2+4k)·G1+(2mk+2k2+4k)·G2，主私钥msk 包含(m2+mk+2m)·Zp，功能密钥sky包含(m+k+2)·Zp，3IPFE 方案的功能密钥为sky :=(-y⊤W，y)，其中y 是公开的、无需秘密保存，因此这里未将它计入sky 的大小中.密文ct 包含(2m+2k+3)·G1，解密Dec计算mk+2k2+3k个配对运算.

4.2 内积功能加密方案的抗泄漏CCA 安全性证明

下面给出所设计内积功能加密方案IPFE 的抗泄漏CCA 安全性定理以及安全性证明.

定理1(IPFE 的抗泄漏CCA 安全性) 令容许的泄漏比特数κ ≤logp-2λ且内积函数的多项式上界X ＜.4“X ＜/4” 这一要求实际上自然是成立的，因为p 为配对群的阶数， p 至少为2λ 比特的，故/4 为安全参数λ 的指数大小，显然远大于多项式大小的X=poly(λ).如果Dk-MDDH 假设在群G1和群G2上均成立，同时H是抗碰撞哈希函数，则图3 中构造的内积功能加密方案IPFE 是κ-LR-CCA 安全的.

具体而言，对于任意PPT 敌手A，其攻击IPFE 的κ-LR-CCA 安全性且进行最多Q次ODEC查询，存在PPT 敌手B1，B2，B3，使得

证明:我们将通过定义一系列不可区分的游戏 G0—G5来进行证明，其中游戏 G0为原始的安全实验，而在游戏G5中敌手A攻破安全性的优势几乎为0.为了方便起见，表2 中给出了这些游戏的简要描述，并用灰色标记出相邻两个游戏间的差别.我们用Pri[·]表示某个事件在游戏Gi中发生的概率.

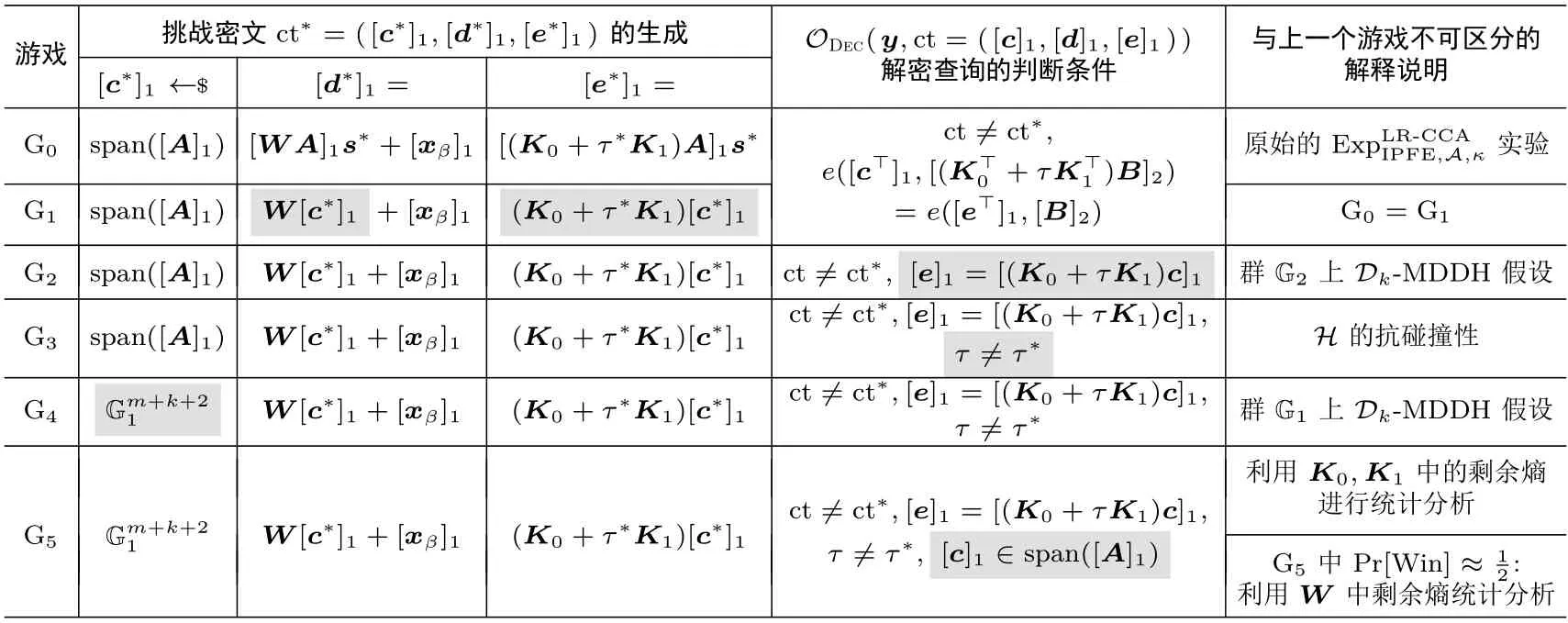
表2 内积功能加密方案IPFE 的抗泄漏CCA 安全性证明中游戏G0—G5 的简要描述Table 2 Brief description of games G0–G5 for LR-CCA security proof of IPFE

游戏G0: 该游戏为IPFE 的实验(参见图2).令事件Win 表示β′β.根据定义可知

— 通过OKGEN(y)查询，A可以获得功能密钥sky(-y⊤W，y);通过OLEAK(y，L)查询，A可以获得泄漏信息L(sky)L(-y⊤W，y);通过OMLEAK(L) 查询，A可以获得泄漏信息L(msk)L(W).A通过OLEAK和OMLEAK获得的密钥总泄漏量不超过κ比特.

— 在收到A的ODEC(y，ct([c]1，[d]1，[e]1)) 查询时，挑战者如下进行回复.挑战者首先判断是否有ct/ct*∧e([c⊤]1，[(+)B]2)e([e⊤]1，[B]2) 成立，其中τ:H([c]1，[d]1).如果不成立，则挑战者直接输出⊥给A.如果成立，则挑战者计算[d]1:-y⊤W[c]1+y⊤[d]1，并在[-mXY，mXY] 范围内求解离散对数d.如果能够求解得到d，挑战者将解密结果d输出给A;否则，挑战者输出⊥给A.

— 在收到挑战向量(x0，x1) 时，挑战者如下生成挑战密文ct*:([c*]1，[d*]1，[e*]1): 挑战者均匀选取s*←$计算[c*]1:[A]1s*，[d*]1:[W A]1s*+[xβ]1，τ*:H([c*]1，[d*]1)Zp和[e*]1:[(K0+τ*K1)A]1s*.

为了防止平凡攻击，敌手A进行的所有OKGEN(y) 查询必须满足〈x0，y〉〈x1，y〉，且A不能在获得挑战密文ct*之后继续进行OLEAK和OMLEAK查询.

游戏G1: 该游戏与上一游戏G0几乎一样，差别仅在于挑战密文ct*的生成.在该游戏中，挑战者在计算挑战密文ct*([c*]1，[d*]1，[e*]1) 中的[d*]1和[e*]1时，按如下方式进行计算: [d*]1:W[c*]1+[xβ]1，[e*]1:(K0+τ*K1)[c*]1，即不再使用[c*]1[A]1s*中的向量s*.

由于[c*]1[A]1s*，因此这些变化只是形式上的，G1和G0本质是相同的，故

游戏G2: 该游戏与上一游戏G1几乎一样，差别仅在于对解密查询ODEC的回复.在该游戏中，对于A的ODEC(y，ct([c]1，[d]1，[e]1)) 查询，挑战者的判断条件改为:

如果上述条件不成立，则挑战者直接输出⊥给A.

为了分析Pr2[DecBad]，注意到事件DecBad 发生意味着

即[e⊤]1-[c⊤(+)]1为[B]2内核(kernel) 里的一个非零向量.

根据引理3，Dk-MDDH 假设比Dk-KerMDH 假设更强，因此可知在计算意义上是很难找到[B]2内核里的非零向量的.故在群G2上的Dk-MDDH 假设下，事件DecBad 几乎不会发生，有Pr2[DecBad]≤(λ)+1/(p-1) 成立，从而命题1 得证.

游戏G3: 该游戏与上一游戏G2几乎一样，差别仅在于对解密查询ODEC的回复.在该游戏中，对于A的ODEC(y，ct([c]1，[d]1，[e]1)) 查询，挑战者的判断条件进一步改为:

其中τ:H([c]1，[d]1) 和τ*:H([c*]1，[d*]1) 分别为本次ODEC查询中计算的标签以及挑战密文ct*的生成过程中计算的标签.如果上述条件不成立，则挑战者直接输出⊥给A.

命题2基于H的抗碰撞性，有

证明:令事件TagColl 表示A进行过某次ODEC查询(y，ct([c]1，[d]1，[e]1))，使得有ct/ct*，[e]1[(K0+τK1)c]1，但ττ*成立.显然G2和G3在事件TagColl 不发生的情况下是完全相同的，因此有

为了分析Pr3[TagColl]，我们将事件TagColl 分为以下两种情况，并逐一进行分析:

根据引理2，群G1上的Dk-MDDH 假设成立能推出Uk-MDDH 假设和U(m+k+2)，k-MDDH 假设均成立.而根据群G1上的U(m+k+2)，k-MDDH 假设，在计算意义上难以判断[c*]1到底是从中均匀选取的还是从span([A]1){[A]1s*|s*}中选取的.因此，G3和G4是计算不可区分的，我们有

游戏G5: 该游戏与上一游戏G4几乎一样，差别仅在于对解密查询ODEC的回复.在该游戏中，对于A的ODEC(y，ct([c]1，[d]1，[e]1)) 查询，挑战者的判断条件进一步改为:

如果上述条件不成立，则挑战者直接输出⊥给A.

命题3

证明:令事件CBad 表示A进行过某次ODEC查询(y，ct([c]1，[d]1，[e]1))，使得有ct/ct*，[e]1[(K0+τK1)c]1，τ/τ*，但[c]1/span([A]1) 成立.显然G4和G5在事件CBad 不发生的情况下是完全相同的，因此有

事件CBad 发生意味着A的某次ODEC查询(y，ct([c]1，[d]1，[e]1)) 满足ct/ct*，τ/τ*，[c]1/span([A]1)，以及

下面说明A难以计算出满足上述条件的[e]1.首先由于τ/τ*，因此上式中的(μ0+τμ1) 与A所获得的信息(μ0+τ*μ1) 两两独立，故对于A而言，(μ0+τμ1) 在Zp上均匀分布.此外，由于[c]1/span([A]1)，前面选择的向量a⊥满足(a⊥)⊤c/0.因此，对于A而言，上式中的(μ0+τμ1)b⊥(a⊥)⊤c这一项在span(b⊥){γb⊥|Zp}上均匀分布，从而A能计算出满足上述条件的[e]1的概率不超过1/p.

根据上述分析，在A的一次ODEC查询中，事件CBad 发生的概率不超过1/p.因此，在A的Q次ODEC查询中，事件CBad 发生的概率不超过Q/p，即Pr5[CBad]≤Q/p，从而命题3 得证.

最后给出对Pr5[Win] 的分析.

命题4

证明:对于A提交的挑战向量(x0，x1)，令Δx1-x0为其差值.由于我们考虑的是多项式有界内积函数，因此‖x0‖∞≤X，‖x1‖∞≤X，即x0，x1[-X，X]m，故有Δx1-x0[-2X，2X]m.

综上分析，除了ct*之外，A能获得的关于u的信息最多只有κ比特.因此对于A而言，中至少还有(m+2)logp-κ比特的最小熵.

接下来分析G5中Win 发生的概率，即A能够猜对β的概率.在挑战密文ct*([c*]1，[d*]1，[e*]1)中，注意到仅[d*]1的计算涉及β:

综上所有分析，结合式(2)—(4)以及命题1—4，可以得到式(1)成立.

因此图3 中构造的内积功能加密方案IPFE 是κ—LR-CCA 安全的，定理1 得到证明.

4.3 抗泄漏安全功能加密方案的效率分析及比较

本小节对本文方案与已有的抗泄漏安全功能加密方案的效率进行分析和比较.

第1 节中已介绍，目前抗泄漏安全功能加密的相关工作较少，仅有的方案包括Wang 等人[43]构造的抗泄漏CCA 安全的功能加密方案以及Zhang 等人[44，45]构造的抗泄漏CPA 安全的内积功能加密方案.表1 中对这些方案的抗泄漏安全性进行了比较.下面将对这些方案的效率进行分析和比较，包括各项参数大小及算法运行时间.

表3 中分析和对比这些方案的各项参数大小，包括主公钥mpk、主私钥msk、功能密钥sky以及密文ct 的大小，其中表中的数字表示包含的群元素个数(如“m2+m” 表示包含m2+m个群元素)，“m” 为内积函数的向量维数，“logp” 为群阶p的比特长度(在128 比特安全强度下，一般有logp256).由表3 数据可知，本文方案的主公钥mpk 大小比文献[43] 方案要小(大约小m/4 倍)、比文献[44，45] 方案稍大(大约大4 倍)，主私钥msk 大小比文献[43—45] 方案均要大(大约大m/2 倍)，功能私钥sky大小比文献[43—45] 方案均要小(大约小3 倍)，而密文ct 大小比文献[43] 方案稍大(大约大2 倍)、比文献[44，45]方案要小(至少小128·m+512 倍).总的来说，本文方案的各项参数大小与已有方案[43-45]各有优劣，而在最影响通信复杂度的密文ct 大小方面，本文方案比文献[43] 方案稍大，但远小于文献[44，45] 方案.

表3 抗泄漏安全功能加密方案的各项参数大小比较Table 3 Comparison of leakage-resilient secure FE schemes: Parameter sizes

图4 中分析和对比了这些方案的算法运行时间，包括设置算法Setup、密钥生成算法KGen、加密算法Enc 以及解密算法Dec 在不同向量维数m下的运行时间.运行时间分析采用了libgnark 库[53]中的BN254 曲线.由于文献[43] 方案的KGen 和Dec 算法中分别涉及混淆电路的混淆算法和求值算法，其计算复杂度与混淆电路的层数、门数等参数息息相关，难以分析出实际的运行时间，因此在图4 的KGen 和Dec 算法的运行时间中，我们仅分析和对比了文献[44，45] 方案和本文方案.由图4 数据可知，本文方案的设置算法Setup 比文献[43] 方案快大约1—3 个数量级、比文献[44，45] 方案稍慢(不超过1 个数量级)，密钥生成算法KGen 比文献[44，45] 方案稍快(不超过1 个数量级)，加密算法Enc 比文献[43] 方案快大约2—7 个数量级、比文献[44，45] 方案快大约1—3 个数量级，解密算法Dec 比文献[44，45] 方案快大约2个数量级.总的来说，本文方案的算法运行时间比已有方案[43-45]有较大优势，特别是在操作最为频繁的加密算法Enc 和解密算法Dec 方面，本文方案比已有方案快1—7 个数量级.

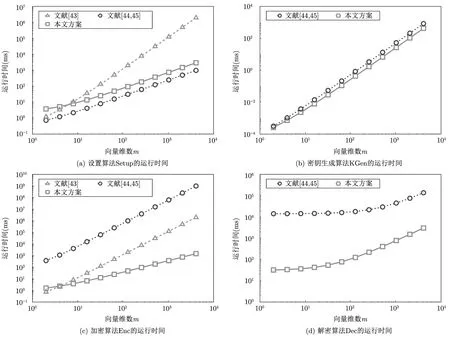
图4 抗泄漏安全功能加密方案的算法运行时间比较Figure 4 Comparison of leakage-resilient secure FE schemes: Running time of algorithms

5 总结

本文提出了第一个达到适应性抗泄漏CCA 安全性的内积功能加密方案.本文方案所达到的抗泄漏 CCA 安全性是完全适应性的，允许敌手以任意的适应性的方式进行四种查询，包括主私钥泄漏查询、功能密钥泄漏查询、功能密钥查询以及解密查询，比已有工作中考虑的功能加密抗泄漏安全性[43-45]都要强.所提方案为非对称配对群上的直接构造，不使用复杂的密码原语，相较已有工作而言构造更为简单.我们基于标准的MDDH 假设证明了方案的抗泄漏CCA 安全性，且方案支持的泄漏率优于Zhang 等人[44，45]构造的抗泄漏CPA 安全内积功能加密方案.在本文工作的基础上，如何进一步提高抗泄漏CCA 安全内积功能加密方案的效率以及支持的泄漏率可作为后续的研究方向.