煤矿瓦斯抽采巷小直径TBM转弯位姿控制研究与应用

陈良发，谭家贵，汪义龙，蔡昌伟，王冰山，金鲁华，周全超，杨 阳

(1.华能煤业有限公司，北京 100070；2.华能云南滇东能源有限责任公司矿业分公司白龙山煤矿一井，云南 曲靖 655508；3.华能煤炭技术研究有限公司，北京 100070)

近年来我国的TBM发展迅速，作为目前隧道掘进最先进的设备，小直径TBM在煤矿岩巷的施工作业中大大提高了掘进速度与安全性[1-3]。为了保持TBM掘进路线与拟定路线一致，需要对TBM在隧道岩巷掘进过程中刀盘的位姿进行控制，控制器性能的优劣对TBM刀盘位姿与隧道的位置、走向有着重要的影响[4，5]。因此，对煤矿瓦斯抽采巷小直径TBM的转弯位姿控制器开展研究。

目前国内外学者对TBM的姿态控制及轨迹跟踪技术开展了以下研究：张强等基于空间齐次变换矩阵对盾构机进行位姿正解，并根据各液压缸杆长建立位姿反解数学模型，并在MATLAB中验证了模型的准确性[6]；Yue M等通过设计滑模鲁棒控制器解决了盾构机掘进过程中变负载情况下的盾体姿态纠偏问题[7]；邵诚俊通过搭建TBM的多系统耦合动力学模型探究装备的纠偏轨迹规划与轨迹纠偏控制[8]；任颖莹等多名学者研究了模糊PID控制与估计自动跟踪控制相结合的控制算法[9-12]；黄威等将盾构姿态引入盾构水平受力平衡分析中，建立基于二维盾体结构提出一种力学与水平姿态理论分析模型[13]；吴惠明等基于支持向量机提出一种预测盾构机姿态及优化施工参数的方法，该方法拟合优度高、准确性好[14]；Wang L等针对盾构机推进系统液压缸建立运动模型，设计了基于主从控制方法的复杂地层盾构机位姿控制方法[15]；Zhou C等采用混合深度学习模型提出了一个预测性的框架用以解决盾构掘进过程中的位姿控制问题，并使用隧道工程采集到的盾构姿态与位置数据验证该框架模型具有较高的预测精度[16]；Wang X等搭建了一个土壤-机械耦合模型以预测隧道掘进过程中盾构机所受载荷，并进行逆运动学求解以描述因盾构机姿态调整引起的雅克比速度与土壤位移[17]；Bui等基于切割有限元方法有效地模拟TBM在隧道中的推进过程，能够提前对隧道的挖掘情况进行预测以实现对TBM位姿的预测与控制[18]；Gabriel等提出一种基于深度学习的三步骤智能决策系统，能够针对TBM掘进过程中传感器的测量值实时为操作员提供预测值，以实现对TBM位姿的提前预测与控制[19]。目前TBM施工中，TBM刀盘、机身的姿态与轨迹调节主要是通过全站仪、刀盘位移传感器等仪器测量并由主司机控制调整盾构机掘进参数以对轨迹偏差进行调节，在该调节过程中反馈经常滞后且调节效果与操作人员的工作经验相关，不正确的人工操作常导致隧道位置与走向偏差较大、隧道超挖与欠挖、TBM卡机等现象的发生。因此，开展TBM智能掘进技术是未来TBM发展的必然趋势。本文提出的基于主从分区速度控制方法的推进系统液压缸PID控制器在未来少人、无人化智能掘进施工能够发挥更大的作用。

目前国内外研究针对煤矿岩巷掘进环境下的小直径TBM的位姿控制研究还相对较少，笔者对小直径TBM的位姿控制方法进行了研究。

1 工程背景

滇东矿业分公司白龙山煤矿一井位于云南省曲靖市富源县老厂矿区，地处滇、黔、桂三省邻接地带的云南省富源县东南部，是云南省根据“西电东送”能源战略部署而新建的第一对大型现代化矿井。白龙山煤矿一井为煤与瓦斯“双突”矿井，目前处于基本建设时期。传统的钻爆法施工工艺在“双突”条件下瓦斯治理的复杂工艺下，工期和进度难以保证，特别是瓦斯抽采巷道的施工与现场的结合，全断面隧道掘进机(TBM)进行煤矿巷道建设施工的方法无论是在工期、造价亦或是工程技术等方面均具有显著优势，该矿井为实现智能化煤矿建设，计划采取TBM结合现场实际进行技术研究和应用。

白龙山煤矿一井具备TBM施工条件的瓦斯抽采巷主要为101采区和102采区的抽采巷，101采区总长度合计2810 m，102采区总长度合计为9638 m，边界巷转弯半径均大于100 m，均可满足TBM转弯施工要求。为保障施工安全性，防止煤与瓦斯突出事故发生，瓦斯抽采巷底板与煤层顶板的法距应始终保持在20 m左右层位，TBM施工过程中采用超前钻机对前方不少于120 m的距离进行超前探测，获知掘进巷道前方下部煤层厚度变化情况，后续TBM掘进时需根据煤层厚度变化及时调整位姿，因此需要一种实时、稳定的控制方法来辅助主司机调整TBM位姿，从而提高施工安全性。

2 TBM推进系统联合仿真模型

2.1 TBM动力学模型

由于TBM刀盘位姿与掘进路径改变均是通过控制刀盘推进油缸伸出的位移实现的，因此在进行TBM推进系统的三维模型建立时，重点对推进油缸进行建模，而对刀盘、主驱动，机体等部位进行简化建模。某小直径TBM的推进系统由8个液压缸组成，液压缸两个一组，共上、左、下、右四组推进液压缸。将简化后的TBM三维模型导入ADAMS动力学仿真软件。

首先为TBM模型添加约束副，重点是对推进液压缸部分的约束进行细化，而简化刀盘、盾体，撑紧盾等结构的约束。TBM掘进过程中，驱动力由推进系统的推进液压缸提供，表现为液压缸缸筒与液压缸杆之间的相互作用力，负载力则由岩体施加，同时为各个机械结构之间的约束副添加摩擦力(前盾与推进液压缸杆之间的球铰副、推进液压缸筒与撑紧盾之间的球铰副、液压缸杆与液压缸筒之间的圆柱副均要设置机械摩擦力)。岩体对TBM施加力作用在前盾上，掘进时刀盘阻力模拟为前盾上、下、左、右四个作用点上的单向作用力，再通过设置衬套力模拟TBM机体周向受力，通过在AMAMS中测量四个力作用点的速度并将掘进负载力设置为与速度相关的函数[20]。完成约束添加与力添加之后的模型如图1所示。

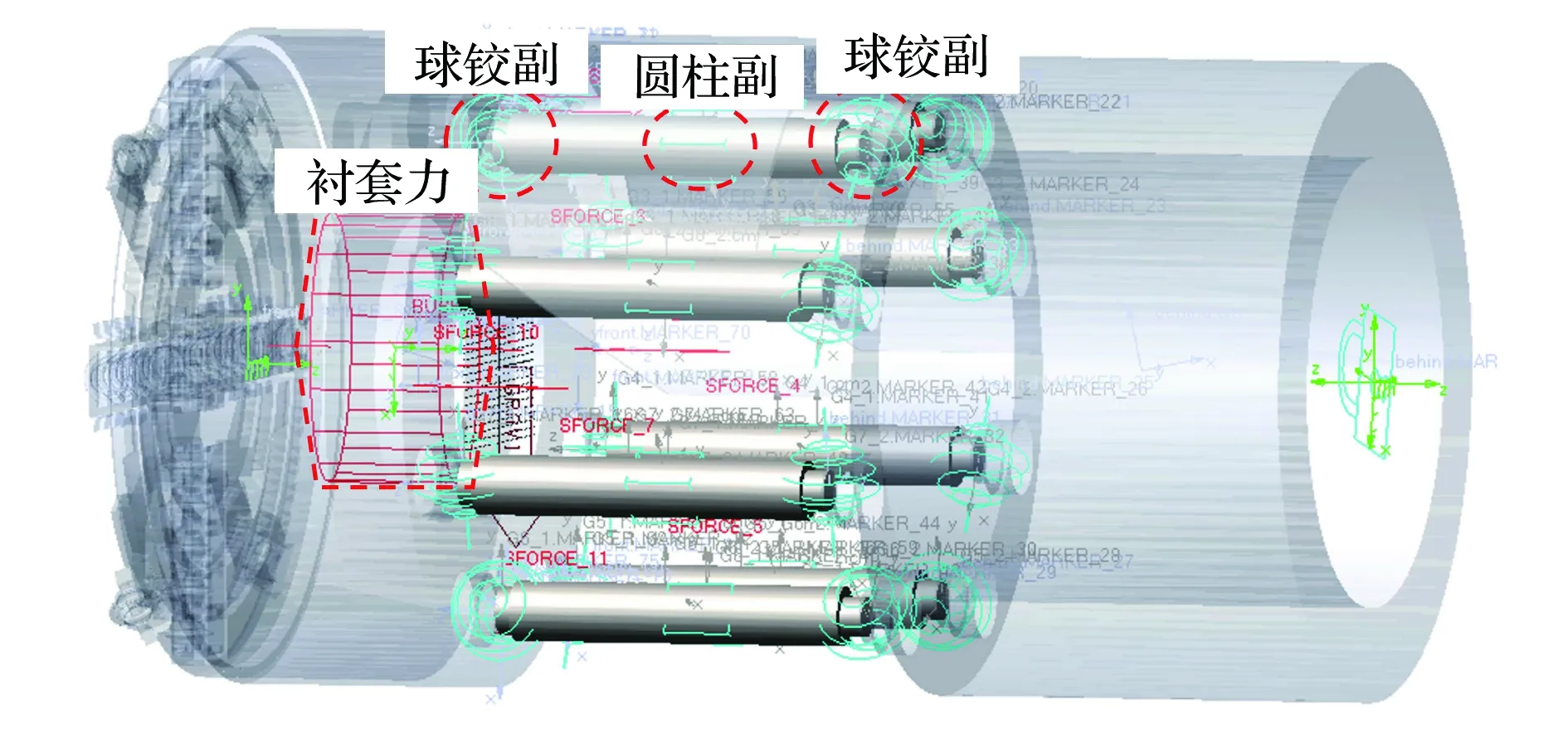
图1 TBM动力学模型

2.2 TBM推进系统液压仿真模型

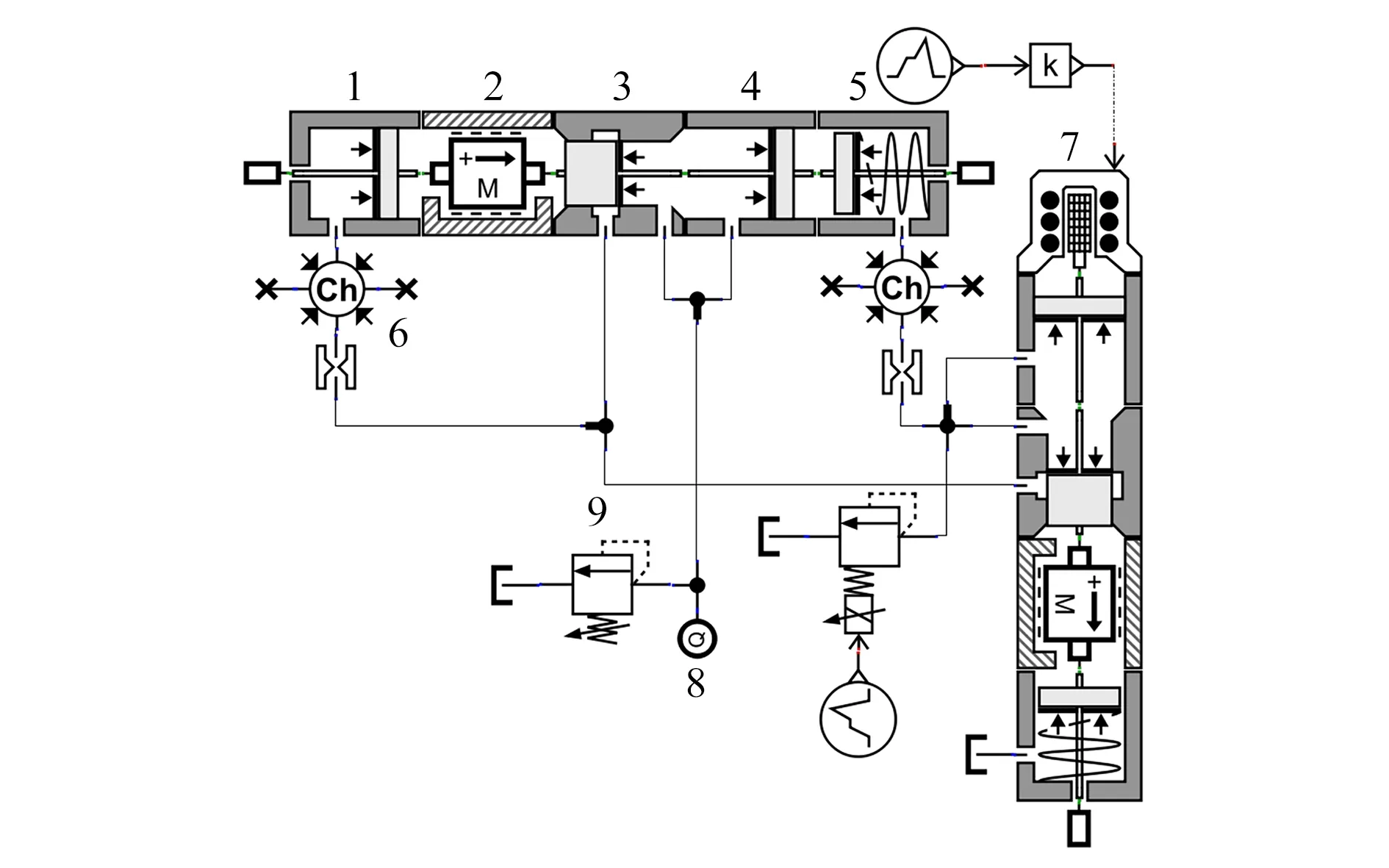
TBM推进系统单分区液压原理如图2所示，该单分区液压系统主要包含恒压变量泵、安全阀、三位六通换向阀、比例调速阀、比例溢流阀与推进液压缸。在建立TBM推进液压系统时，只考虑掘进过程中液压缸伸出的工况，不再对液压缸杆收回过程进行仿真，因此，可以简化省略换向阀，系统中采用恒压变量泵，在仿真模型中也可使用恒压源来替代，并对液压系统中的比例调速阀与比例溢流阀搭建HCD(Hydraulic Component Design)模型。做出以上简化可以减少仿真运算的时间，提高仿真效率。

1—电机；2—恒压变量泵；3—安全阀；4—三位六通换向阀；5—比例调速阀；6—比例溢流阀；7—推进液压缸

在AMESim中对比例调速阀与比例溢流阀进行HCD模型搭建，比例调速阀定差减压阀和比例节流阀两部分组成。定差减压阀控制端分别与比例节流阀进、出油口相连。当比例调速阀进出口压差增大时，减压阀阀芯左移，减压阀流道变窄，压损增大；相反，比例调速阀进出口压差减小时，减压阀阀芯左移，流道压损降低，从而使节流阀压差近似保持定值。因此定差减压阀的输出流量可通过调节比例节流阀控制电流成比例的进行调节，不受压力变化的影响。比例调速阀HCD模型如图3所示；比例溢流阀通过比例电磁铁控制阀芯左端弹簧的推力，当油液压力小于弹簧的推力时，比例溢流阀阀芯关闭，系统中油液全部流入执行器。当系统油液压力高于电磁铁推力时，阀芯左移，比例溢流阀流道打开，部分油液溢流，由于阀芯左端弹簧被压缩，系统油液压力随阀芯位移的增加而增大。

1—活塞①；2—一维平移质量；3—带环形孔的阀芯；4—活塞②；5—带弹簧的活塞③；6—液压容积与压力动力学模型；7—力输入转化模块；8—恒流源；9—溢流阀

对于推进液压缸及负载模型，将掘进过程所受负载力简化为恒力和具有运动速度的粘弹性模型，设置负载力与速度之间为一次函数模型，从而将液压缸推进速度与负载力创建联系。

为了实现TBM动力学模型与单分区液压模型之间的数据交换，建立AMESim与ADAMS联合仿真数据接口。从ADAMS动力学模型中输出8个推进油缸的位移、TBM掘进位移、刀盘的倾覆角与横摆角；从AMESim液压模型中输出八个推进油缸的液压力，为ADAMS动力学模型提供驱动力，通过ADAMS/Controls模块将模型导出生成.inf文件，并添加到AMESim液压模型当中，TBM机-液联合仿真模型搭建完毕，如图4所示。

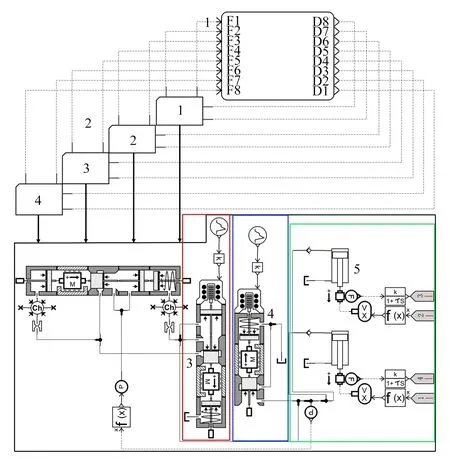
1—联合仿真数据交换模块；2—分区推进系统超级元件；3—比例调速阀；4—比例溢流阀；5—推进液压缸及负载

3 瓦斯抽采巷设计轴线参数化表征

由于煤层分布位置并不是始终不变的，为了抽出煤层中含有的瓦斯，TBM在掘进煤矿瓦斯抽采巷的过程中需要进行位姿调控以保证瓦斯抽采巷轴线位置距煤层基本不变。本研究假设瓦斯抽采巷设计轴线仅在竖直方向上(X方向)产生变化，而水平方向上位移暂不考虑。TBM在竖直方向上的设计轴线可以划分为三种曲线的组合，分别为直线、圆曲线与缓和曲线，其中缓和曲线作为设计轴线中直线与圆曲线之间的过渡线，以保证刀盘倾覆角不发生突变，确保TBM掘进过程的稳定性。TBM在转向时刀盘与盾体之间会产生倾角，其中竖直方向上的倾角为倾覆角，水平方向上的倾角为横摆角。下面对直线、圆曲线、缓和曲线、倾覆角与横摆角进行参数化表征。

3.1 直线型瓦斯抽采巷设计轴线

首先建立固定坐标系与运动坐标系，以撑紧盾盾尾圆心为固定坐标系原点(x，y，z)，以刀盘中心点为运动坐标系原点(x0，y0，z0)，s表示刀盘中心点运动轨迹的长度，TBM实际位姿的倾覆角与横摆角表示为α、β；期望的倾覆角与横摆角则表示为α0、β0。

直线型瓦斯抽采巷设计轴线如图5所示，假设TBM整机长度为L，则运动坐标系原点位于固定坐标系的(0，0，L)处。

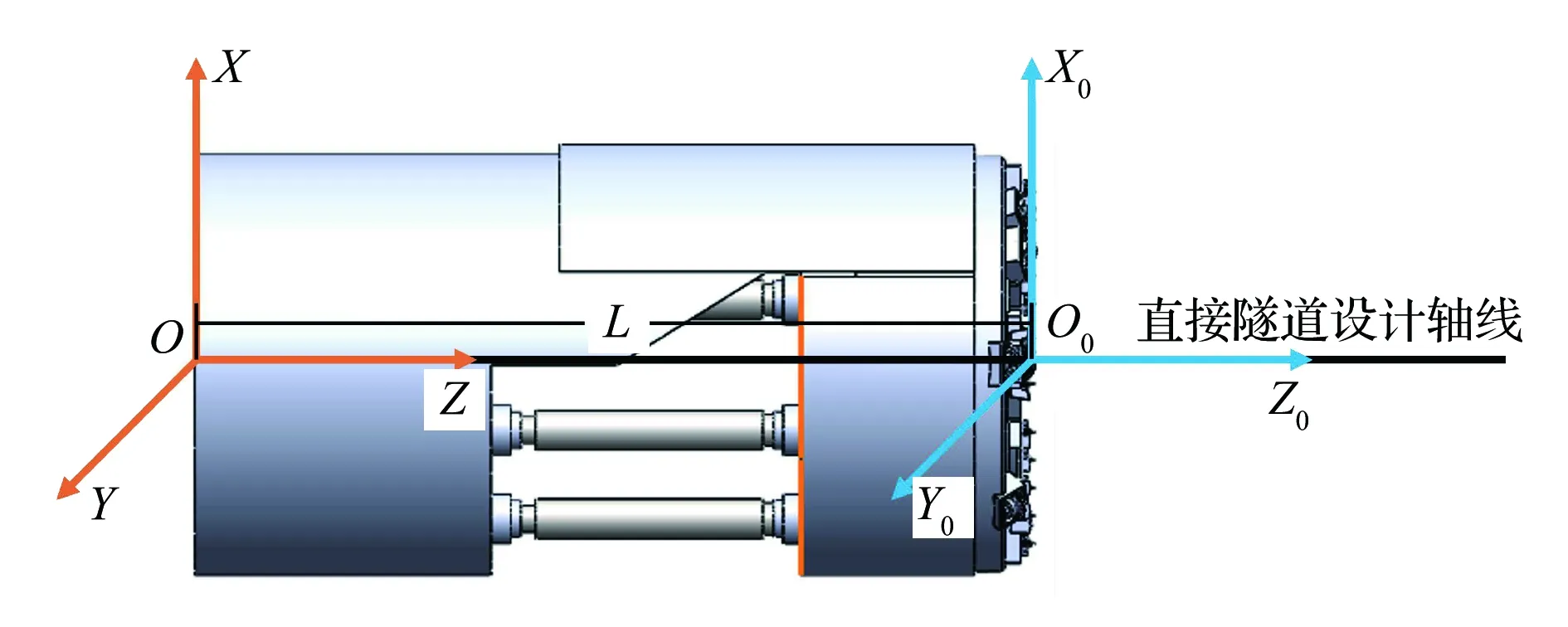
图5 直线型瓦斯抽采巷设计轴线示意

随着TBM掘进，随着掘进距离s的增加，动坐标原点O0相对于固定坐标系的坐标可以表示为：

TBM的期望倾覆角与横摆角可表示为：

3.2 圆曲线型瓦斯抽采巷设计轴线

圆曲线型瓦斯抽采巷设计轴线示意如图6所示，当TBM按照竖直曲线掘进时，运动坐标系原点O0可以由固定坐标系表示为：

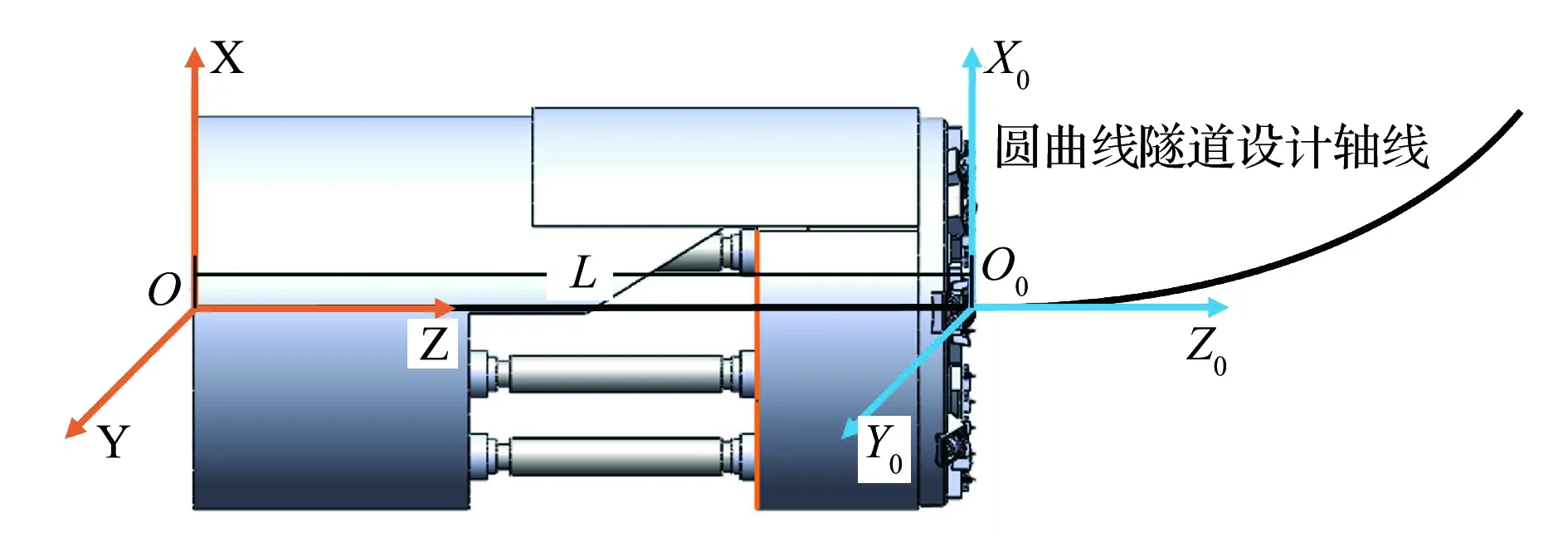
图6 圆曲线型瓦斯抽采巷设计轴线示意图

沿圆曲线隧道设计轴线掘进时，TBM的期望倾覆角与横摆角表示为：

式中，R为期望圆曲线的半径。

3.3 缓和曲线型瓦斯抽采巷设计轴线

缓和曲线的作用是充当直线掘进段与圆曲线掘进段之间的过渡曲线段，缓和曲线拥有当TBM位移增加，其曲率半径逐渐增大至圆曲线半径的特性，因此缓和曲线的参数表征与圆曲线半径以及自身设计长度有关。缓和曲线型瓦斯抽采巷设计轴线示意如图7所示，当TBM按照竖直曲线掘进时，参考回旋缓和曲线参数设计方法，运动坐标系原点O0可以由固定坐标系表示为：

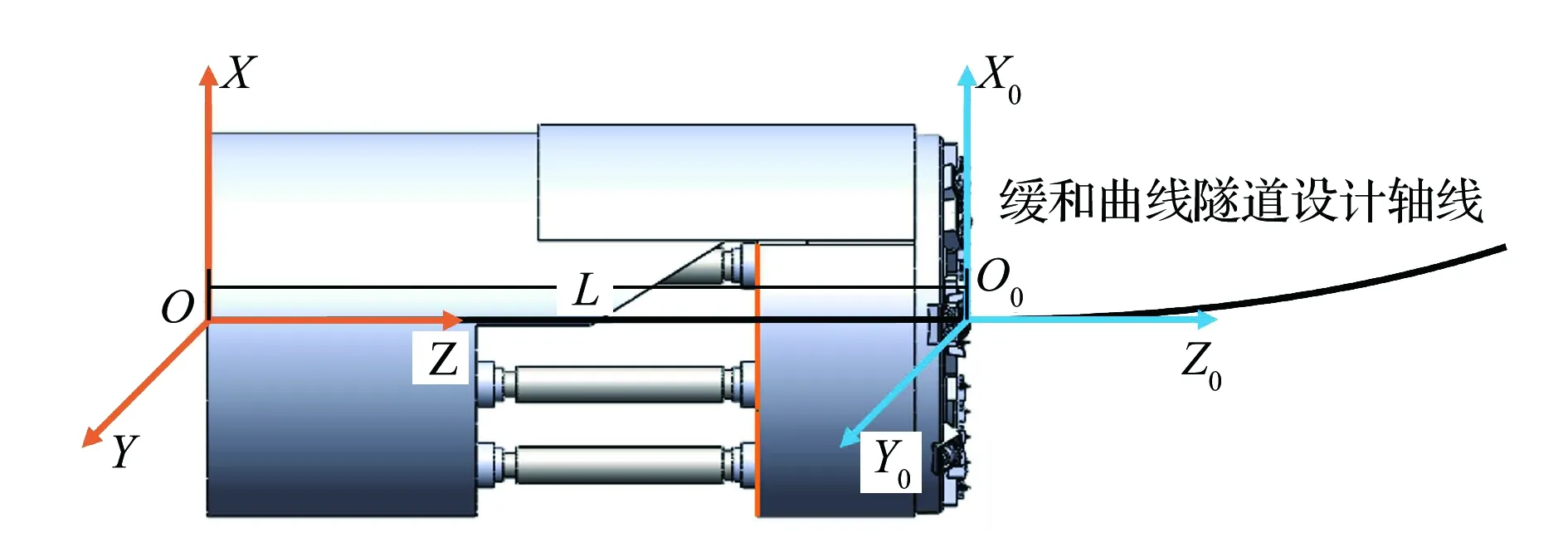
图7 缓和曲线型瓦斯抽采巷设计轴线示意

沿圆曲线隧道设计轴线掘进时，TBM的期望倾覆角与横摆角表示为：

式中，s0为缓和曲线的设计长度。

4 PID控制器设计与仿真分析

4.1 PID控制器设计

传统的TBM控制系统是开环控制系统，对于偏差信号没有反馈响应，无法对偏差进行纠偏处理，系统控制误差大，而PID控制通过比例、积分、微分三个环节对偏差信号进行处理，其结构简单、鲁棒性好。本研究采用PID控制将TBM的控制系统变为闭环控制，以实现对偏差及时纠正，保证TBM位姿的正确与稳定。

本研究采用推进系统液压缸主从控制方案，其原理是选定一组液压缸作为主推进分区，将TBM期望掘进速度作为期望信号输入，并返回该组液压缸实际速度信号，两信号的偏差作为控制量进行PID控制调节，PID输出不同大小的电流信号控制调速阀阀口开度以确保该组缸推进速度稳定，选取上分区液压缸作为主分区进行速度调节。在确定主分区后，对剩余三个分区液压缸分别进行PID调节，由于前文已经推导了TBM掘进距离s与期望倾覆角α0、期望横摆角β0之间的数值关系，因此通过在ADAMS动力学模型中测量TBM掘进距离便能够计算出TBM在该掘进距离时的期望倾覆角与横摆角。对于下分区液压缸，在AMESim中设置输入信号为期望倾覆角，反馈信号为在ADAMS动力学模型中实时测得的TBM倾覆角，并对偏差进行PID控制，输出电流信号控制调速阀阀口开度以对倾覆角进行调节；而对于左分区和右分区，输入信号为计算得到的期望横摆角，反馈信号为实时测得的横摆角，并对偏差进行PID控制。最终搭建完成的控制模型如图8所示。

1—联合仿真数据交换模块；2—分区推进系统超级元件；3—PID主从控制模块；4—比例调速阀；5—比例溢流阀；6—推进液压缸及负载；7—主缸速度PID模块

4.2 控制效果仿真分析

分别对三种设计轴线进行仿真分析，以ADAMS输出的掘进距离s为自变量，分别设置f(s2)=0、f(s2)=s/R、f(s3)=s2/2Rs1来计算直线、圆曲线和过渡曲线下的期望倾覆角，并作为PID控制的输入信号，由于本研究仅考虑TBM在竖直方向上的转弯，因此期望横摆角均设置为0。三种设计轴线下均设置上分区液压缸期望速度为1 mm/s；对上、左、下、右四组推进液压缸均设置相同的负载力-速度关系，大小为3.6×106N/(mm·s-1)；考虑到岩体强度不均匀，设置随机载荷10000 N；设置圆曲线半径为500 m，设置缓和曲线轴线长度为50 m。下面对三种设计轴线进行仿真分析。

4.2.1 直线型设计轴线

直线型设计轴线仿真得到的倾覆角与横摆角变化曲线如图9所示，由图9(a)可知直线型设计轴线仿真情况下的倾覆角与横摆角均在3.2 s左右稳定在0 rad上下波动，倾覆角波动幅值为8.4×10-6rad，横摆角波动幅值为8.8×10-6rad；而0～3.2 s之间角度摆动较大，其原因主要是因为上分区液压缸期望速度设置为1 mm/s，由于液压系统自身延迟，其余分区的液压缸提速较慢，导致偏角摆动较大，而由于随机载荷的影响，稳定状态下倾覆角与横摆角上下波动。

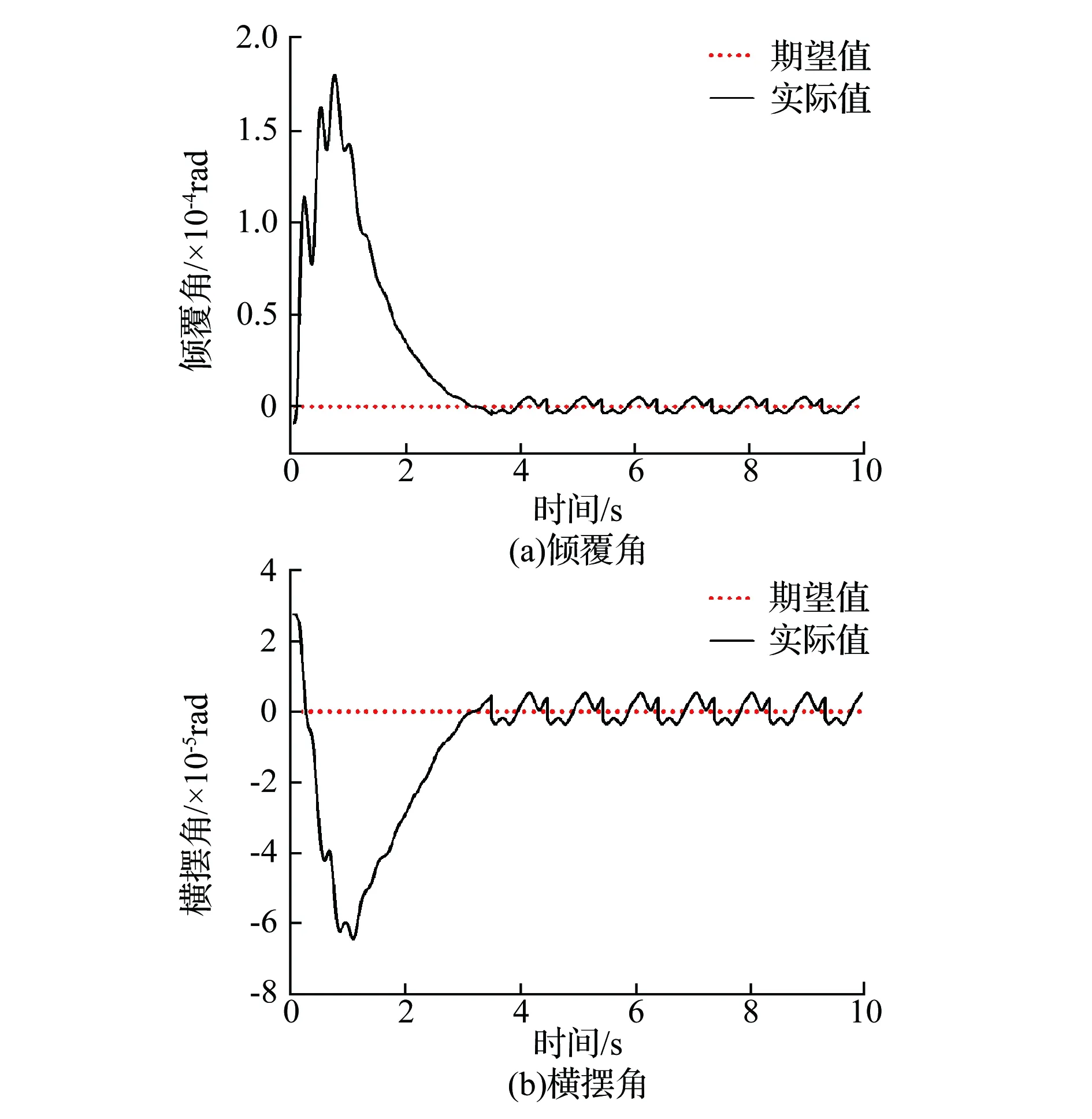
图9 直线型设计轴线倾覆角与横摆角

4.2.2 圆曲线型设计轴线

圆曲线型设计轴线仿真得到的倾覆角与横摆角变化曲线如图10所示，其中横摆角仿真结果与直线型设计轴线相基本相同，根据式(4)可知，倾覆角α大小与TBM掘进距离s成线性关系，且直线斜率为1/R，图10(a)中倾覆角的实际值在稳定状态下逐渐上升，且在期望值上下波动，倾覆角波动幅值为1.0×10-5rad，控制效果良好。

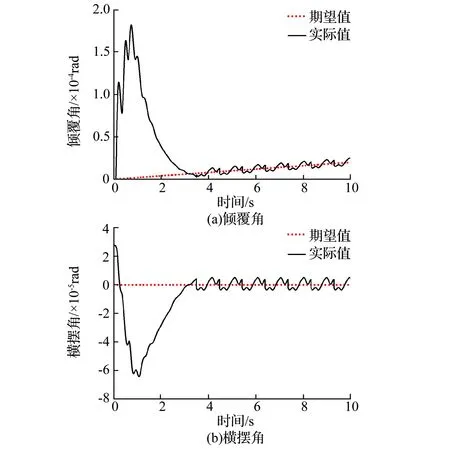
图10 圆曲线型设计轴线倾覆角与横摆角

4.2.3 缓和曲线型设计轴线

为缓和曲线型设计轴线仿真得到的倾覆角与横摆角变化曲线如图11所示，由于缓和曲线是直线与圆曲线之间的过渡曲线，因此在缓和曲线初始阶段与直线基本相同。由图可知，缓和曲线下TBM倾覆角与横摆角变化规律与直线设计轴线下的变化规律基本相同。

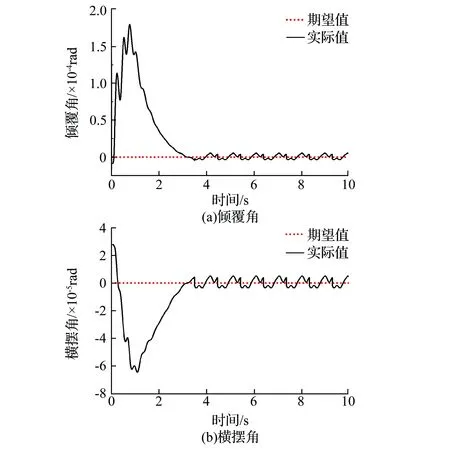
图11 缓和曲线型设计轴线倾覆角和横摆角

5 实验仿真对比分析

为验证该位姿控制器的可行性，选取某煤矿巷道小直径TBM转弯段施工掘进数据与仿真模型得到的结果进行对比。在小直径TBM按照拟定路线掘进施工过程中，刀盘上下左右四个方位布置的角位移传感器与位移传感器能够实时检测TBM刀盘的倾覆角与横摆角等位姿状态，同时，刀盘推进液压缸上布置有位移与压力传感器，用于实时反馈各推进缸的伸出位移与压力变化。使用PLC控制器将传感器采集到的模拟信号转换为真实的物理量，并在主控室上位机上显示。同时，这些数据被储存在上位机中，供主司机使用以根据信息控制和调整设备掘进参数。

将煤矿巷道预先拟定的期望倾覆角变化数据导入本文搭建的小直径TBM位姿控制器中，在ADAMS动力学模型中注入该巷道掘进前期收集记录的负载压力、速度、位移数据作为工况参数，通过联合仿真输出TBM掘进过程中倾覆角仿真变化数据，对数据进行插值拟合处理生成控制器仿真倾覆角变化曲线，并与TBM掘进该煤矿运输巷时采样得到的实际TBM倾覆角数据曲线进行对比分析，仿真与实际倾覆角随时间变化曲线如图12所示。

图12 仿真与实际倾覆角变化曲线

由图12可知，经过控制器调控后的TBM倾覆角与拟定的倾覆角变化更贴合，且控制过程倾覆角变化无较大的波动与突变，控制效果相较于人为操控更平稳、更具有实时性，能够较好地为主司机提供掘进轨迹预测参数，以实现TBM位姿辅助控制的作用效果。

6 结 论

1)依托煤矿瓦斯抽采巷需求，建立了小直径TBM动力学仿真模型与推进液压系统仿真模型，并建立数据交换接口，实现了TBM机-液联合仿真模型的建立。

2)将TBM掘进路线拆解为三种类型，分别对直线、圆曲线和缓和曲线时TBM的x、y、z位置坐标与倾覆角α、横摆角β进行参数化表征，以用于TBM的位姿控制。

3)搭建了基于主从分区速度控制方法的PID控制器，利用TBM机-液联合仿真模型分别对主分区缸组(上分区)进行速度控制，以倾覆角和横摆角为控制目标对其余三组缸分别进行PID控制调节。仿真结果表明TBM位姿角在3.2 s左右稳定，且在期望值附近上下波动，倾覆角与横摆角稳定情况下波动幅值均在1.0×10-5rad以下，该PID控制器对小直径TBM位姿控制效果良好。

4)本研究针对煤矿瓦斯抽采巷进行小直径TBM转弯位姿控制研究，瓦斯抽采巷多侧重于竖直方向倾覆角位姿控制，该控制方法同样可以推广至小直径TBM在俯仰与横摆等多种形式转弯位姿控制工况下应用。