基于FEM和RSM方法的异形环轧制型腔填充难度评价方法

2023-11-21胡阳刘东杨艳慧王建国吕楠饶浩东

西北工业大学学报 2023年5期

胡阳, 刘东, 杨艳慧, 王建国, 吕楠, 饶浩东

(西北工业大学材料学院, 陕西西安 710072)

异形环件轧制工艺是一种先进的金属塑性成形工艺,广泛应用于各种复杂截面形状的无缝环件生产,如轴承环、法兰环、齿轮环和火车轮。与传统锻造工艺相比,它具有生产成本低、生产效率高、内部质量好、精度高等优点[1-2]。然而,异形环的几何结构相当复杂,沿轴向各部位的体积分布有明显的差异,使得异形环件轧制过程中金属流动难以控制,型腔难以填充[3]。

国内外的学者通过试验、数值模拟的手段对异形环件的轧制过程进行了大量研究。Moussa等[4]最早探讨了在异形环件轧制过程中,如何在保证环件外径达标的同时,型腔能够恰好填充完整,并指出有很大一部分异形环并不能通过矩形环件直接轧制成形,对于一些变形量大、截面形状复杂的环件甚至需要多个阶段不同轧制型腔的轧制成形。Lee等[5]基于均匀体积分布单元技术和极限轧制比,提出了一种异形环件两段式轧制过程中间坯的设计方法,成功实现了挖掘机轮辋的精确成形,但这种两段式的轧制方式大大提高了生产周期及生产成本。Park等[6]在锻造阶段将原材料加工成形为初始异形环坯,再通过单道次轧制成形为最终产品形状,并通过有限元分析优化了环坯形状,以最短的轧制时间来生产尺寸精度最高的环件。文献[7-10]也采用了类似的方式对各类异形环坯轧制成形为异形环件的过程进行了有限元仿真分析,同样地都出现了环件截面心部应变偏小的现象,即使增加初始环坯的壁厚能够在一定程度上增大心部的变形量,但整个轧制时间的增加也会造成环件靠近表面区域温度偏低的现象,进而影响组织性能。目前,对于异形环件轧制工艺,普遍的做法是采用加大最终环件的加工余量,简化轧制型腔,以方便型腔填充,保证尺寸完整,但这种方式极大增加了材料成本。另一方面,在不提高材料成本的前提下期望保证型腔的填充完整性,也常会采用异形环坯,或是设计中间辊进行多道次轧制的成形方式,如此一来,不论是需要设计额外的多套型腔模具,还是多道次轧制方式所需要人工、时间、能耗的增加,都会提高生产成本。然而,对于异形截面环件的型腔填充难度始终未有一个成熟的评价方法,用来优化轧制型腔的设计。

因此,本文以台阶型环件为研究对象,将FEM方法与RSM方法相结合,提出了一种通用的异形环件型腔填充难易程度评价方法。为了实现这一目标,基于对轧制型腔的描述,定义了3个设计变量和相应的响应目标。应用Simufact有限元仿真软件建立了该台阶型环件轧制过程的有限元模型,基于模拟结果建立并优化了目标函数的响应模型,通过该响应模型,全面研究了不同变量对优化目标的影响。最后,结合响应目标的等值线图得出了该台阶型环件轧制型腔基于环件最大轴向体积变化率的填充难易程度评价方法。

1 异形环件轧制型腔的设计理念

在异形环件轧制中,为了减少多道次轧制带来的额外生产成本,在非必要情况下通常采用矩形环坯一道次轧制成形,这就必须在设计异形环件的轧制型腔时对型腔的填充难度进行考量:该异形环件是否能由矩形环坯直接轧制成形。

图1为一个常见的台阶型环件,图中的内轮廓为环形零件的截面形状,外轮廓为需要设计的轧制型腔形状。可以看出,该环形零件的上下端面及外环面形状相对简单,在单边余量确定的情况下,将3个方向加上余量直接设计为直边即可。而内环面形状相对复杂, 但仔细观察后发现上下近似为对称的形状,可以将其设计为对称式的2个台阶,这在一定程度上也能够降低异形环件的轧制难度。

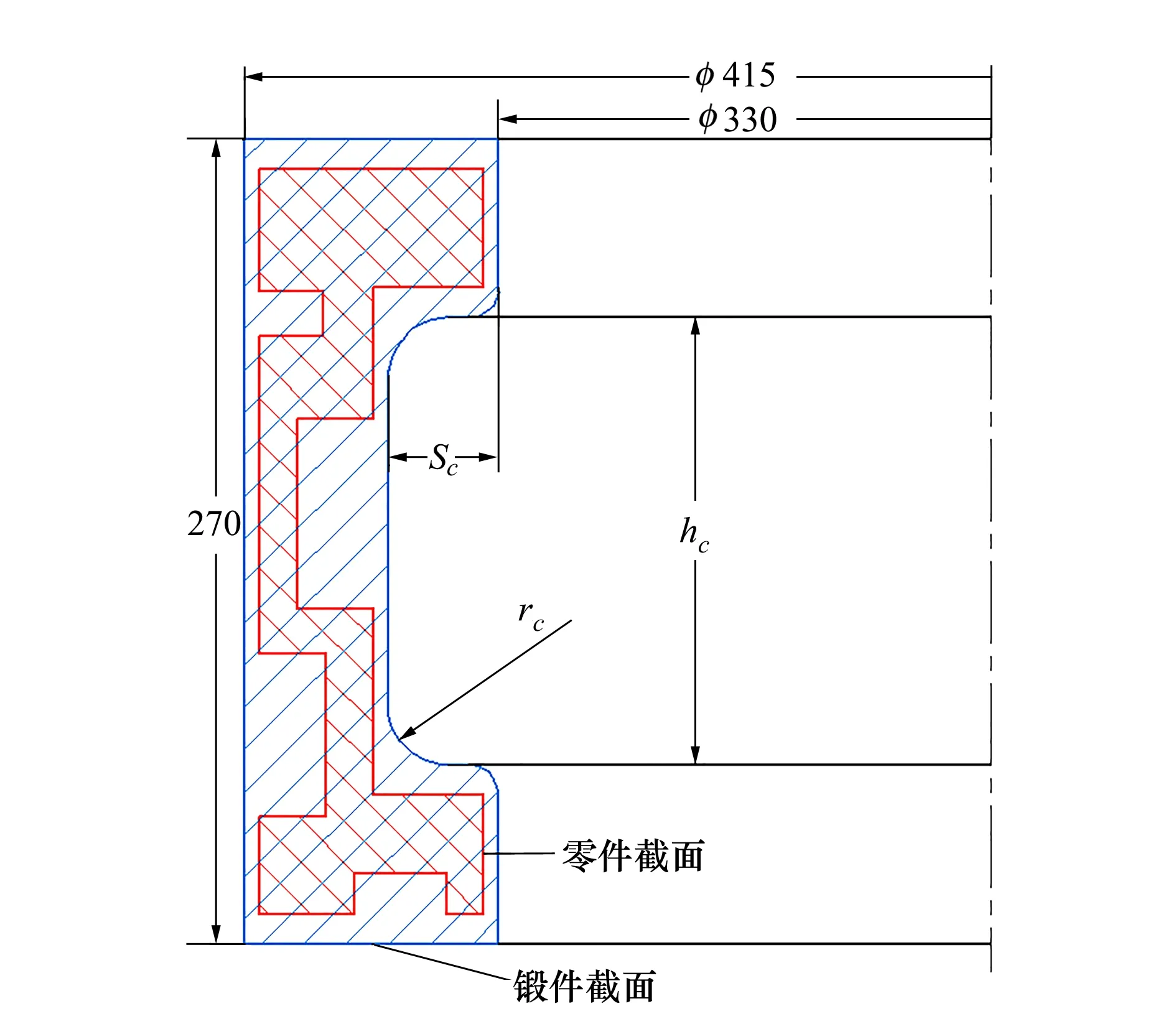
图1 型腔设计图

为了更为直观地表现环件的截面轮廓形状,假设环件的高度为h,将环件沿高度方向分为h等份后,则可以得到环件轧制前后单位高度上的轴向体积分布分别为:

由此可以得到轧制前后环件的轴向体积变化率为:

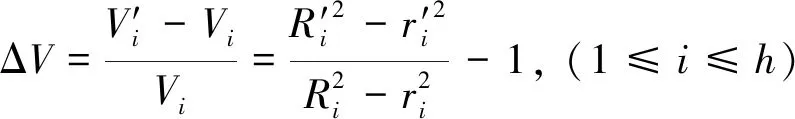
(3)

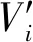
根据公式(3)绘制了由矩形环坯轧制成形台阶型环件过程的轴向体积变化率(见图2),可以发现,轧制过程中,凹槽处的坯料不断减少并向两端台阶处流动填充,且两端台阶处的轴向体积变化率最大,说明这部分的填充难度最大。因此,在设计轧制型腔时,内环面凹槽的高度hc,宽度sc及圆角rc的大小就是决定型腔填充难度的关键。具体的参数设计将在后续详细叙述。

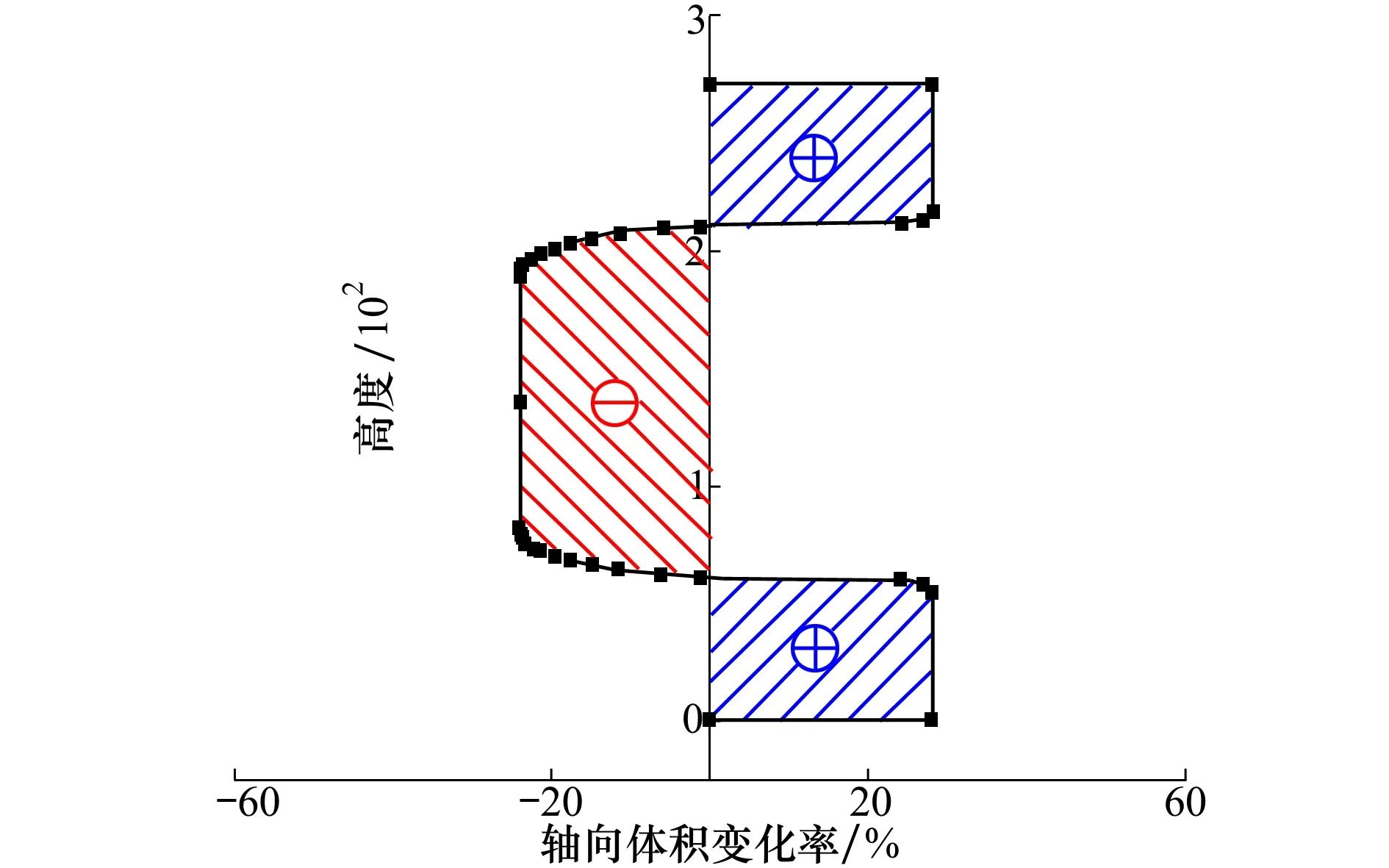
图2 环件轧制前后的轴向体积变化率

2 有限元模型的建立

基于Simufact有限元软件建立了台阶型环件轧制过程的三维热力耦合有限元模型,如图3所示。在该有限元模型中,各个轧辊被设定为刚性体,在轧制过程中不允许存在塑性变形,材料均为5CrNiMo,而环件则被设定为弹塑性变形体,材料为GH4738合金,2种材料的热力参数[11-12]列于表1中,同时采用文献[13]中所建立的Arrhenius方程来表示GH4738合金的本构模型。

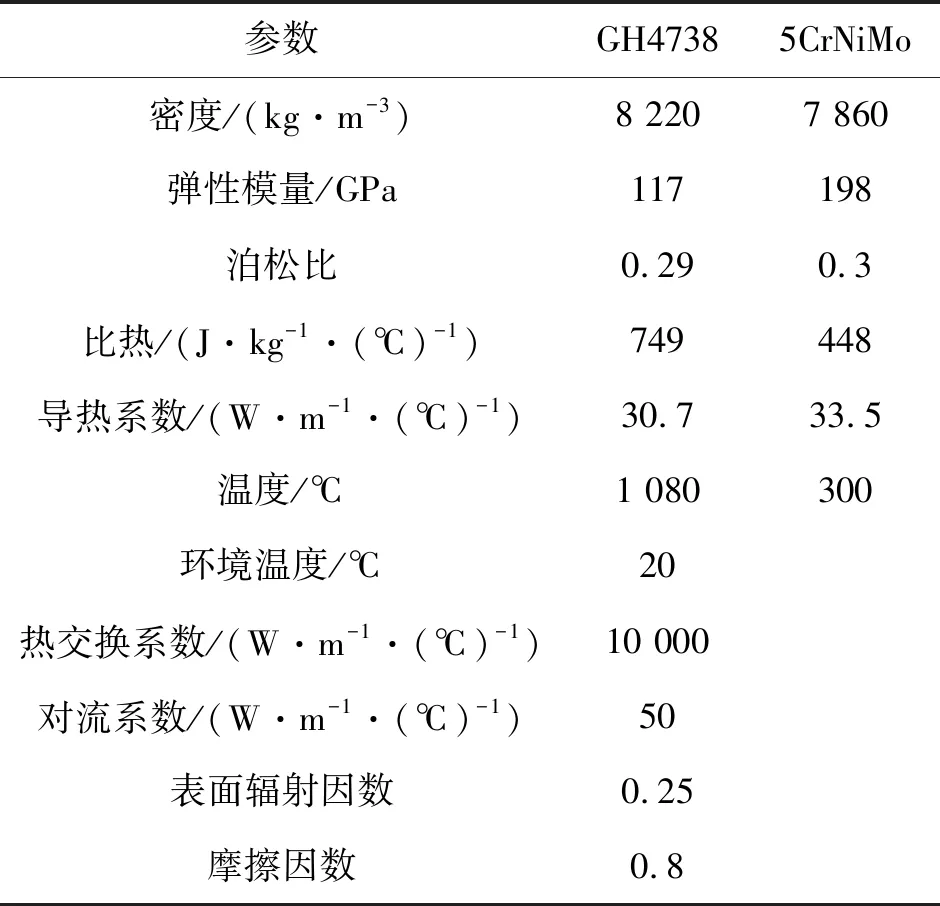
表1 模拟过程中的热力参数

图3 三维热力耦合模型

在该台阶型环件轧制的模拟中,所有的轧辊运动都与实际的轧制过程一致。主辊以1.5 rad/s的恒定速度旋转,芯辊在坯料的带动下被动旋转,同时以给定的进给曲线向前运动,如图4所示。抱辊的移动由测量辊控制,测量辊测量环件的实时外径,并反馈至抱辊控制系统,以控制环件的平稳轧制。锥辊的旋转速度与环件端面的实时线性速度相匹配,同时随着环件的增长而后退。

图4 芯辊进给曲线

3 响应面设计

响应面法是一种数学方法和统计方法相结合的产物,常用来针对多个变量进行建模和分析,以达到优化目标响应值的目的[14-15]。一般的流程为:

1) 设计独立变量及目标函数,并确定变量的取值范围;

2) 设计试验,并按照试验方案执行试验;

3) 拟合出数学响应模型;

4) 响应模型精度的验证与修正;

5) 获取最优的变量组合。

3.1 设计变量的选择

如前文所述,对于本文所选取的台阶型异形环件而言,上下端2个台阶处的填充难度最大,而凹槽的尺寸大小恰恰是填充的关键,因此在设计轧制型腔时,应充分考虑内环面上凹槽尺寸的大小对型腔填充的影响。根据设计原则,在单边余量确定后,分别选取内环面凹槽的宽度sc,高度hc以及圆角rc作为3个设计变量(见图1),即:

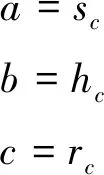
(4)

由3个设计变量即可确定轧制型腔余下的所有尺寸。同时,由于需要给零件留下机加及探伤的余量,因此设计变量a,b还需要满足下列不等式:

另一方面,a,b的值不能太小,当a,b趋近于0时,轧制型腔截面近似于矩形,显然这是没有意义的,而c的范围并没用特殊限制,因此本文给定a,b,c的范围如下:

3.2 目标函数的构建

为了实现台阶型异形环轧制过程的多目标型腔优化,将轧制结束时型腔的缺损率作为响应目标φ,由公式(10)确定。

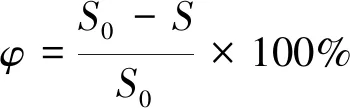
(10)

式中:S0为轧制型腔的截面积;S为轧制结束时环件的实际轴向截面积;φ的值越趋近于0表示型腔缺损率越小,型腔填充越完整。

针对台阶型异形环件轧制过程型腔优化设计的数学描述可定义为:

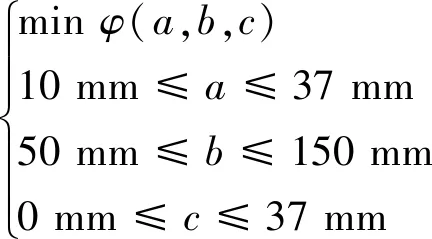
(11)

3.3 试验方案的设计

本试验采用三因素、五水平的中心复合设计,包括1个中心点、6个轴点和8个顶点共15个样本点。为了统一变量的范围,采用公式(12)对设计变量a,b,c的值进行编码转换,编码后的变量记为η1,η2,η3。

(12)

式中:λ为对应的设计变量的值;ηi为编码变量的值;λmax和λmin分别是该设计变量的最大值和最小值。因素水平如表2所示。

表2 中心复合设计因素水平表

通过该三因素五水平的中心复合设计可以得到20组试验方案,结合Simufact有限元仿真软件进行数值模拟分析,并统计模拟结果列于表3中,其中共有5组重复性试验。需要注意的是,为了避免无关因素的干扰,所有试验方案均采用相同的轧制参数,且成形环件外径、高度和最大壁厚一致,环坯截面尺寸一致,仅轧制型腔尺寸和对应矩形环坯的内外径略有不同。

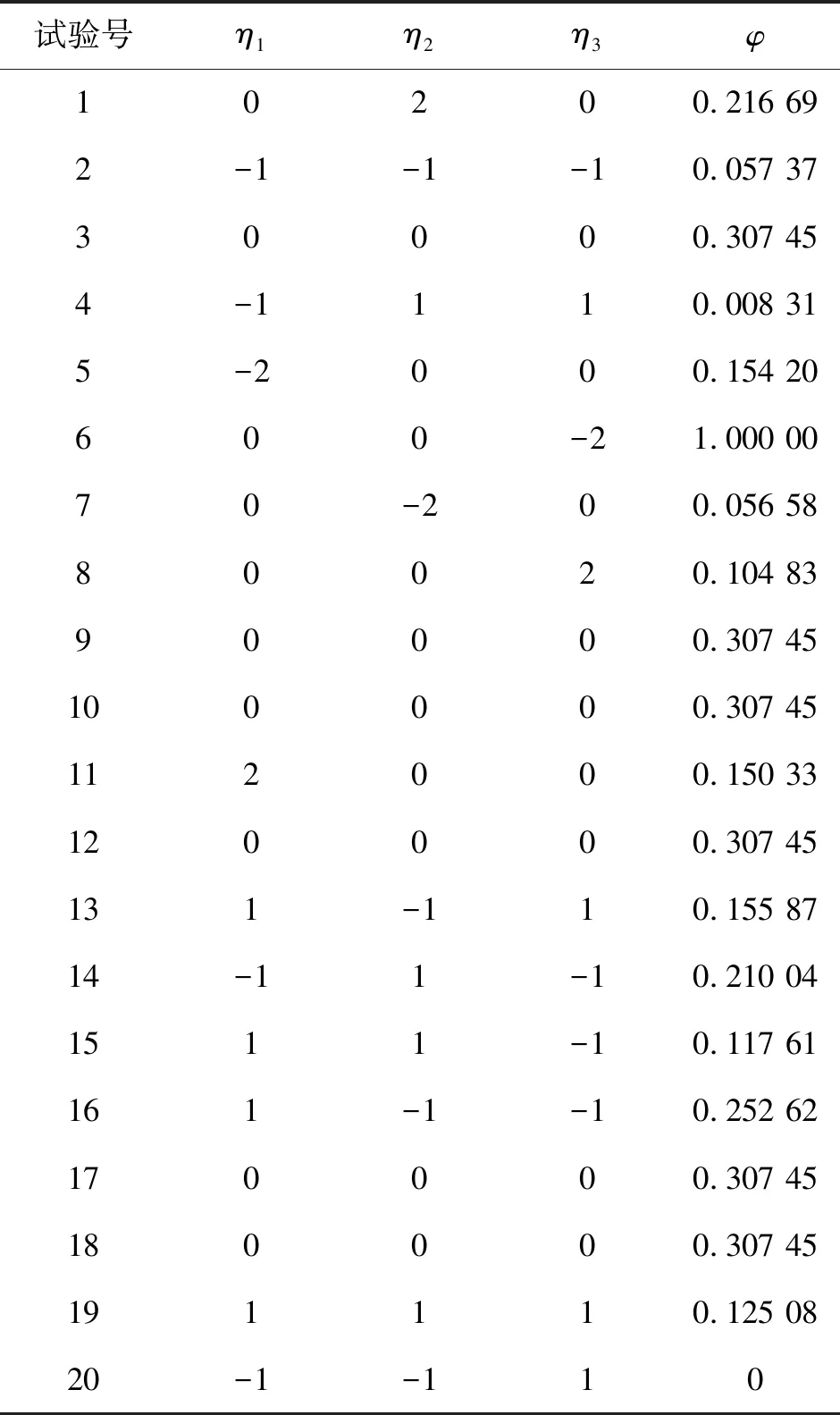
表3 试验方案和模拟结果

3.4 响应模型的构建

响应面法的基本思想是通过构造一个多项式来代替实验和数值模拟,以近似描述目标函数与设计变量之间的响应特性。因此,本文以二阶模型为基础(见公式(13)),应用最小二乘法建立目标函数φ关于设计变量的响应。

(13)

为了检验响应模型的拟合精度,对响应模型中各项进行了显著性分析和方差分析(ANOVA)。其中P值为一个概率值,用来判断各项的显著性,P值越小,表明对应项的显著性越高,响应模型越理想,相反地,当P值较大时,表明该对应项的显著性不高,应该在进一步的分析中被剔除。在去除了回归值P较大的项后,得到了改进后的目标函数φ关于设计变量的响应模型:

表4和表5分别为响应模型的显著水平和方差分析,T值和F值分别代表了平均值检验和方差检验,其中若F值远大于1,则说明各组均值间的差异具有统计学意义。从响应模型(14)的ANOVA分析结果可以看出,响应模型中各项均具有较好的显著性,模型的拟合程度也达到80.79%,说明该响应模型是合适的,能够很好地描述目标函数φ与各个设计变量之间的响应关系。

表4 响应模型(14)中各项的显著水平

表5 响应模型(4～19)的方差分析

4 结果与讨论

根据表3的结果可以看出,不同试验方案,其响应值的优劣也大不相同,例如试验20拥有最小的φ值,试验15拥有相对较小的φ值,试验6拥有最大的φ值。选取试验6、试验15和试验20这3组典型方案作为分析目标进行对比。图5为3组试验的填充情况对比图,可以发现,适当减小凹槽宽度及高度,可以降低型腔填充难度,但过度减小型腔的异形程度反而会大大增加锻件质量,提高生产成本,就如试验20中的结果一样,即使型腔缺损率几乎为0(见图5c)),锻件的质量却足足增加了134%;另一方面,减小凹槽圆角,能有效降低锻件质量,但当圆角减小到一定程度时,反倒不利于型腔的填充,出现如图5a)所示的情况。因此,在轧制型腔的设计过程中,3个设计变量需要互相协调,才能在保证型腔填充率的同时,不至于过分增加锻件质量,造成坯料的浪费,图5b)中试验15的结果就是锻件设计较为合理的型腔填充情况。

图5 不同试验方案下的型腔填充情况

图6为利用响应面法得到的响应函数φ分别关于不同变量的三维曲面图及二维等值线图。限定型腔截面的填充率在99%以上时,环件的填充质量为合格,则型腔缺损率在1%以上的区域即填充质量为不合格。从图中可以看出,在响应面分析中型腔缺损率1%对应的值为φ=0.26的等值线即为填充合格与不合格的分界线,φ在0.26以上的阴影区域表示填充不合格的情况。

图6 响应目标的二维等值线图和三维曲面图

由图6可知,当η3<-1.3时,型腔缺损率基本在1%以上,属于不合格的区域,说明当凹槽圆角过小的情况下,型腔几乎不可能填充完整;而当η3>0.5时,型腔填充率均在99%以上,属于合格的区域,且响应值φ的曲面曲率变化较小,此时η的变化对型腔的影响已经并不明显了,说明当凹槽圆角处在一个合适大小时,型腔基本能够填充完整。同时,由图2可知,轴向体积变化率最大处位于上下两台阶处,凹槽圆角大小的变化并不会改变其位置。因此,以约束条件为η3=0即凹槽圆角为18.5 mm时,如图6所示目标函数φ关于变量η1和η2的二维等值线图和三维曲面图的情况为例进行讨论。

图7为轧制前后环件的截面尺寸,假设环件轧制前后的内外径、高度、最大壁厚分别为r0,R0,h0,s0和r,R,h,s。则轧制前环件的体积为

图7 轧制前后环件截面尺寸

(15)

而轧制后的台阶型环件形状相对复杂,可将环件分为如图7b)所示的台阶端V1、环件中段V2、凹槽圆角V3三部分体积的组合,分别有:

则轧制结束时环件的体积V可表示为

V=2V1+V2+2V3

(19)

由于约束了不同方案下台阶型环件轧制过程的环坯截面尺寸一致,且最终环件的内外径尺寸也是一致的,故轧制结束时环件的最小壁厚减薄量是不随凹槽尺寸的变化而改变的,即s,s0和R+r的值均为定值。则整个环件截面上下两台阶处为轴向体积变化率最大处,可由公式(20)表示

(20)

可以看出,随着凹槽宽度sc和凹槽高度hc的减小,成型环件的体积逐渐增大,R0+r0的值也随之增大,最大轴向体积变化率ΔVmax逐渐减小。则在图6中,所有型腔填充率达到99%以上的情况里,变量取值在A点处时设计的型腔截面最大轴向体积变化率最大,变量取值在B点处时设计的型腔截面最大轴向体积变化率最小。其中,A点各变量取值分别为η1=0.797,η2=0.619,η3=0,B点各变量取值分别为η1=-0.515,η2=-0.402,η3=0。

由于环件轧制前后体积守恒,则有V=V0,将公式(15)～(19)联立后代入公式(20)可以得到环件最大轴向体积变化率关于台阶型环件轧制型腔各参数的表达式

将A,B两点的变量值通过公式(12)进行转码后代入公式(21)中,即可得到所有填充质量为合格的情况下轧制型腔最大轴向体积变化率的理论安全区间,最大轴向体积变化率最大可取到ΔVmax A=0.149,最小可取到ΔVmax B=0.072。

在异形环件的轧制过程中,当环件上最大轴向体积变化率处的型腔都能填充完整时,整个环件的填充是基本满足合格要求的,因此可以用最大轴向体积变化率来评价型腔的填充难易程度。因此,对于本文所研究的台阶型环件而言,在约束条件为η3=0即凹槽圆角为18.5 mm的前提下,当设计的台阶型环件轧制型腔的ΔVmax>0.149时,填充难易程度为困难,表示在该条件下不论凹槽参数取何值型腔的填充质量几乎不可能合格;当设计的台阶型环件轧制型腔的ΔVmax<0.072时,填充难易程度为容易,表示在该条件下型腔的填充质量几乎都能保证合格;而当设计的台阶型环件轧制型腔的0.072≤ΔVmax≤0.149时,填充难易程度为中等,需要综合考虑型腔截面的设计参数高度hc,宽度sc及圆角rc三者之间的相互匹配关系,只有在保证φ≤0.26的情况下型腔的填充质量才能合格。