基于核心素养的“三角函数的周期性”概念教学策略
2023-11-21惠敏敏
惠敏敏

摘 要:概念是数学的细胞,也是数学思维活动的重要载体。因此,数学概念教学不能止步于让学生熟悉概念、运用概念解题,而应挖掘数学概念的内涵与外延。厘清新授概念与学生熟悉的数学概念、知识间的内在联系,进而创建合适的数学概念生成情境,让数学概念在学生的自主探究中主动生成;让学生习得数学抽象、逻辑推理的具体方法,提升学生的数学核心素养。文章以“三角函数的周期性”公开教学观摩课为例,阐述了数学概念教学中设计探究生成过程的重要性。教师应注重从真实情境出发,逐步引导学生感悟、体会,从而水到渠成掌握数学知识概念。
关键词:三角函数;数学核心素养;教学策略;概念教学
一、教材分析
“三角函数的周期性”是苏教版(2019版)高中数学必修第一册教材7.3“三角函数的图像和性质”的第一节内容。周期性是三角函数的一个典型特征,是后续研究及学习三角函数的图像与性质的基本工具,三角函数周期性的研究也为一般函数周期性的研究奠定了重要基础。
二、学情分析
该堂课是在学生已经学习了函数、角与弧度、三角函数概念等相关知识的基础上开展的。学生来自江苏省四星级高中的普通班,数学学习的基础较好,且在高中阶段的学习已经接近一个学期,数学思维能力有了很大的提升,已具备一定的自主探究能力、数学推理能力及数学抽象能力,可以借助已学知识,采用类比、化归等思想方法完成本节课内容。
三、教学目标
其一,知识与技能。(1)了解周期函数的概念;(2)会判断一些简单的、常见的函数的周期性;(3)会求一些简单的三角函数的周期。
其二,过程与方法。通过众多实例总结探究周期函数,再由周期函数到三角函数的周期性的探索过程,培养学生的数学发现能力和概括总结能力。在研究周期性的过程中,让学生体验由简单到复杂,由特殊到一般的化归思想,并渗透数形结合的思想方法,培养数学的探索能力,学习钻研精神和科學的认知态度,通过小组合作学习培养学生团结协作的精神,体现立学课堂的教学思想.
其三,情感态度与价值观。通过家乡本土的实例引入,培养学生热爱家乡,热爱祖国的情怀。通过各种实例,提炼出共同特性——周期,体会事物间的内在联系,感受类比、化归的思想方法。在探索过程中体会失败与成功的情感体验。
其四,核心素养。以函数与三角函数的基本知识和基本技能为载体,培养学生的数学思维,让学生逐步体会到用数学的眼光去观察世界,用数学的思维来思考世界,用数学的语言来表达世界。在探究周期性和周期函数的概念过程中培养学生数学抽象能力;在由周期特征的实例与已有知识储备函数性质(例如函数奇偶性的概念)的表述中,表示出周期函数的数学语言,培养学生的逻辑推理能力;借助单位圆、三角函数线直观图,培养学生直观想象能力。
四、教学过程
(一)教学环节1:创设情境,引入新课
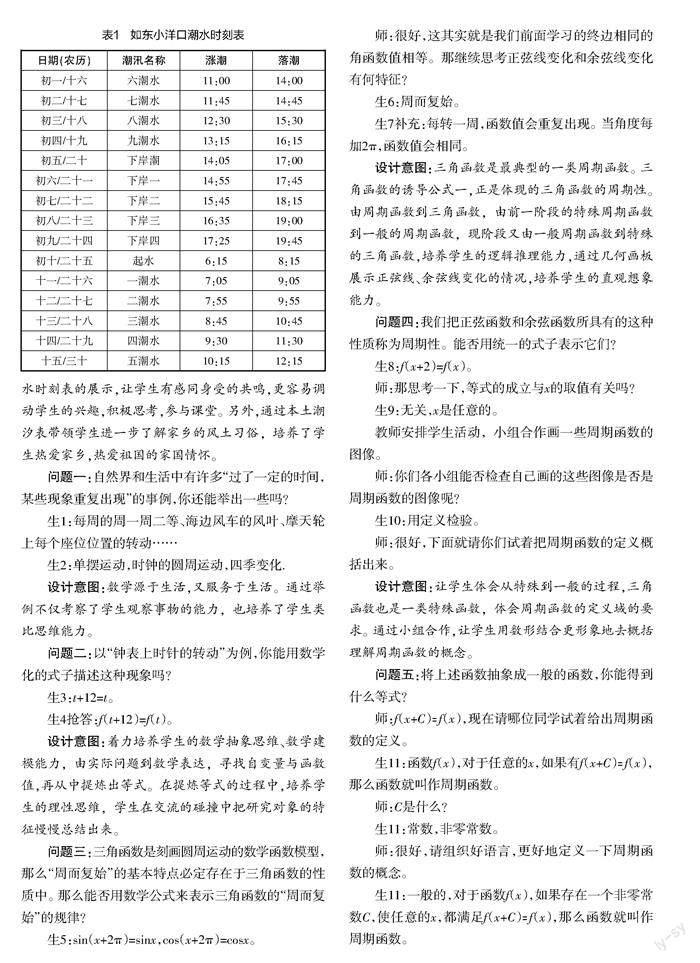
教师导入情境,如表1所示。
设计意图:不少本地学生在小学和初中时,通过在社会实践基地的学习,对潮水涨落有一定了解,而且有不少学生还有过赶海的经历。通过如东本土小洋口潮水时刻表的展示,让学生有感同身受的共鸣,更容易调动学生的兴趣,积极思考,参与课堂。另外,通过本土潮汐表带领学生进一步了解家乡的风土习俗,培养了学生热爱家乡,热爱祖国的家国情怀。
问题一:自然界和生活中有许多“过了一定的时间,某些现象重复出现”的事例,你还能举出一些吗?
生1:每周的周一周二等、海边风车的风叶、摩天轮上每个座位位置的转动……
生2:单摆运动,时钟的圆周运动,四季变化.
设计意图:数学源于生活,又服务于生活。通过举例不仅考察了学生观察事物的能力,也培养了学生类比思维能力。
问题二:以“钟表上时针的转动”为例,你能用数学化的式子描述这种现象吗?
生3:t+12=t。
生4抢答:f(t+12)=f(t)。
设计意图:着力培养学生的数学抽象思维、数学建模能力,由实际问题到数学表达,寻找自变量与函数值,再从中提炼出等式。在提炼等式的过程中,培养学生的理性思维,学生在交流的碰撞中把研究对象的特征慢慢总结出来。
问题三:三角函数是刻画圆周运动的数学函数模型,那么“周而复始”的基本特点必定存在于三角函数的性质中。那么能否用数学公式来表示三角函数的“周而复始”的规律?
生5:sin(x+2π)=sinx,cos(x+2π)=cosx。
师:很好,这其实就是我们前面学习的终边相同的角函数值相等。那继续思考正弦线变化和余弦线变化有何特征?
生6:周而复始。
生7补充:每转一周,函数值会重复出现。当角度每加2π,函数值会相同。
设计意图:三角函数是最典型的一类周期函数。三角函数的诱导公式一,正是体现的三角函数的周期性。由周期函数到三角函数,由前一阶段的特殊周期函数到一般的周期函数,现阶段又由一般周期函数到特殊的三角函数,培养学生的逻辑推理能力,通过几何画板展示正弦线、余弦线变化的情况,培养学生的直观想象能力。
问题四:我们把正弦函数和余弦函数所具有的这种性质称为周期性。能否用统一的式子表示它们?
生8:f(x+2)=f(x)。
师:那思考一下,等式的成立与x的取值有关吗?
生9:无关,x是任意的。
教师安排学生活动,小组合作画一些周期函数的图像。
师:你们各小组能否检查自己画的这些图像是否是周期函数的图像呢?
生10:用定义检验。
师:很好,下面就请你们试着把周期函数的定义概括出来。
设计意图:让学生体会从特殊到一般的过程,三角函数也是一类特殊函数,体会周期函数的定义域的要求。通过小组合作,让学生用数形结合更形象地去概括理解周期函数的概念。
问题五:将上述函数抽象成一般的函数,你能得到什么等式?
师:f(x+C)=f(x),现在请哪位同学试着给出周期函数的定义。
生11:函数f(x),对于任意的x,如果有f(x+C)=f(x),那么函数就叫作周期函数。
师:C是什么?
生11:常数,非零常数。
师:很好,请组织好语言,更好地定义一下周期函数的概念。
生11:一般的,对于函数f(x),如果存在一个非零常数C,使任意的x,都满足f(x+C)=f(x),那么函数就叫作周期函数。
师:任意的x是整个实数集上吗?
生12:应该是定义域内。老师,那周期函数的定义域是不是一定是整个实数集呢?
生13:可以不是整个实数集,比如可以只是整数集,f(x+1)=f(x),也可以是周期函数。
师:很好,那你再完善一下周期函数的定义。
生13:对于函数y=f(x),如果存在一个不为零的常数T,使当x取定义域内的每一个值时,f(x+C)=f(x)都成立,那么就把函数y=f(x)叫作周期函数。
设计意图:总结出周期函数的定义,实现了从特殊到一般的建构。高度概括、表达准确且结论具备一般性。
问题7:若函数f(x)是一个周期函数,C为该函数的一个周期,该函数还有其他周期吗?
生10:2π、-2π、4π、6π等等。
师:很好,你注意到负数也可以,而你这个总结的是三角函数的,一般函数呢?
生11:C、-C、2C、3C、kC等都是。
师:不错,那也就说明周期函数的周期有无数多个,我们最好引入一个最具有代表性的周期,以更方便地描述周期函数的周期。
生12:C。
师:如何命名呢?
学生小声讨论:最小周期?不对,最小还可以是负的,正的最小周期?
师:很好,最小正周期。下面定义一下最小正周期。如果在所有正周期中有一个最小的,则称它是函数f(x)的最小正周期。大家发现如果一个周期函数y=f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫作f(x)的最小正周期。
设计意图:完善周期函数的定义,体会最小正周期引入的必要性,总结出最小正周期的定义。
(二)教学环节2:例题分析
例题:已知函数f(x)是一个周期函数,周期为2,并且f(x)=x2(x∈[0,2)),那么你能否画出整个定义域上的图像?
师:对于这个问题,你想从什么角度切入?
生13:我们只要画出f(x)=x2(x∈[0,2))的图像,那么其余地方的图像都是和这个图像一样的。
生14:更准确地说应该先画出f(x)=x2(x∈[0,2))的图像,其余地方的图像都是由这个图像平移得到的,应该是左右平移得到的。
师:很好,那为什么是左右平移得到的呢?
生14:因为函数f(x)是一个周期函数,周期为2,也就是f(x+2)=f(x)。
师:不错,我们发现对于周期函数,如果能画出一个周期的图像,那么通过周期函数的定义,就可以画出整个函数的图像。同理,如果知道一个周期的解析式,就可以根据定义写出整个定义域的解析式。
教学反思:数学学科核心素养的落实,应该重点关注教学内容与教学结构的环节设计,由外到内逐步深入,合情合理地提出教学问题,以符合学生思维形成过程。对于“三角函數的周期性”的相关学习内容,会涉及以下问题:三角函数为什么会有周期性?三角函数的周期是多少?如何描述一般函数的周期性?教师通过上述三个问题逐步开展教学,可以促进学生形成学习数学的思想和方法,从“科学探究与创新意识”到“科学态度与社会责任”进一步揭示数学学习更高层次的价值追求。
数学概念的教学是培养学生核心素养的重要组成部分,合理设计概念的探究生成过程,是开展教学、落实核心素养教学的基本着力点。教师要创设合理的、实际的问题情境,提出具有开放性、挑战性的问题,以概念的生成发展过程为主线,合理设计教学流程,将数学核心素养与整个教学过程融会贯通,促使学生在主动建构知识体系的过程中实现思维的发展。另外,在教育教学的过程中,要注重在课堂上互相渗透各类数学思想方法,使学生的学习由“散珠”的基本概念形成“串珠”的核心概念。
参考文献:
[1]陆春霞. 追求自然而有深度的数学概念教学[J]. 中学数学研究,2022(09):1-2.
[2]陈唐明. 和数学教师谈如何有效研读教材[J]. 中学数学教学参考,2016(13):60-62.
[3]陈唐明. 本质的角度·思想的高度·思维的效度——高效数学课堂的三个基本维度[J]. 数学教学研究,2014,33(05):2-4+14.
[4]刘长明. 基于核心素养的“三角函数”教材设计与教学思考[J]. 中学数学教学参考,2020(Z1):50-53.
(责任编辑:淳 洁)
