基于小波变换和LSTM神经网络的格陵兰岛近海海域海平面变化预测

赵 健, 刘仁强

基于小波变换和LSTM神经网络的格陵兰岛近海海域海平面变化预测

赵 健, 刘仁强

(中国石油大学(华东) 海洋与空间信息学院, 山东 青岛 266580)

海平面变化包含多种不同时间尺度信息, 传统的预测方法仅对海平面变化趋势项、周期项进行拟合, 难以利用海平面变化的不同时间尺度信号, 使得预测精度不高。本文基于深度学习的预测模型, 提出一种融合小波变换(wavelet transform, WT)与LSTM(long short-term memory, LSTM)神经网络的海平面异常组合预测模型。首先利用小波分解得到反映海平面变化总体趋势的低频分量和刻画主要细节信息的高频分量; 然后通过LSTM神经网络对代表不同时间尺度的各个分量预测和重构, 实现海平面变化的非线性预测。基于该模型的海平面变化预测的均方根误差、平均绝对误差和相关系数分别为12.76 mm、9.94 mm和0.937, 预测精度均优于LSTM和EEMD-LSTM预测模型, WT-LSTM组合模型对区域海平面变化预测具有较好的应用价值。

海平面异常; 小波变换; 长短时记忆网络; 海平面变化; 预测

海平面上升是由气候变暖、极地冰川融化、上层海水热膨胀等引起的全球性环境问题, 是全球气候变化的重要指标。2019年发布的《气候变化下的海洋和冰冻圈》[1]表明: 全球海平面上升速率从1901－1990年的1.4 mm/a增加到 1993－2015年的3.2 mm/a。而NASA(National Aeronautics and Space Administration)、AVISO(Archivage, Validation et Inter⁃prétation des données des Satellites Océanographiques)等机构所确定的1993年至今的全球平均海平面变化速率约为3.3～3.5 mm/a, 不确定度约为0.4 mm/a[2]。作为一种缓发性灾害, 海平面持续升高会造成沿海地区海水入侵、土壤盐渍化、海岸侵蚀等, 同时会破坏沿海国家和地区的生态环境, 成为制约经济发展的重要因素。因此准确掌握海平面变化规律并合理预测海平面变化, 对人口众多、经济发达的沿海地区具有极其重要的科学和现实意义。

海平面异常(sea level anomaly, SLA)是经过一系列大气逆气压、电离层、对流层、潮汐改正的卫星观测瞬时海平面与平均海平面的差值, 可有效反映海平面变化规律, 是海平面变化和中尺度涡研究的重要数据来源。目前海平面变化预报的方法可概括为两类: 气候模型和传统数理统计方法。气候模型主要是利用影响海平面变化的驱动机制, 通过全球海、气、陆及海冰耦合模式实现大尺度海平面变化研究; 传统数理统计方法依据海平面变化的规律进行拟合外推, 多用于区域海平面研究。海平面变化通常可以分为趋势项、周期项、剩余随机项和白噪声等4部分[3], 针对海平面变化的各部分需要采用不同方法进行拟合或分离。传统数理统计方法多采用最小二乘拟合海平面变化的趋势项[4-6], 周期项可以通过经验模态分解、集合经验模态分解、小波分解、奇异谱分析等方法提取[7-9], 剩余随机项可以通过自回归滑动平均[3, 9-10]等模型进行预测。近年来, 随着深度学习算法的深入发展, 各种神经网络因其良好的非线性拟合能力被广泛应用于海平面变化非线性预测中, 如BP(back-propagation)、RBF (radial basis function)、LSTM(long short-term memory)等神经网络[5, 10-13]。孙文等[14]利用20年的卫星测高数据对人工神经网络、支持向量机、自回归滑动平均、摆动灰色模型等方法的预报结果进行比对, 结果表明神经网络对于海平面预测具有更好的适应性。顾小丽等[7]利用RBF神经网络延拓原始数据, 较好地抑制了经验模态分解(empirical mode decomposition, EMD)的端点效应。集合经验模态分解(ensemble empirical mode decomposition, EEMD)的提出有效改善了EMD分解中的模态混叠现象[15], 赵健等[11]提出了EEMD-BP组合模型, 可较好地分解出海平面变化中存在的不同时间尺度信号, 有效提高预测精度。Zhao等[16]提出的SSA-LSTM组合模型, 通过引入LSTM神经网络使得海平面非线性变化预测精度明显提高。虽然已有研究人员对海平面变化的驱动机制进行了较为深入的探讨, 但是使用不同数据和预测方法会导致海平面变化的预测结果存在一定差异, 还需进一步加强海平面变化预测的相关研究。

格陵兰海和挪威海是沟通北冰洋和大西洋海水交换的主要通道, 该区域海平面变化直接反映了北冰洋和大西洋的海水交换情况, 对于掌握北冰洋与北大西洋水文要素、研究高纬地区海平面变化机制具有重要意义。在目前的海平面变化研究中, 大多集中在中低纬度地区, 对于高纬地区海平面变化的研究相对较少。Rose等[17]通过再处理北极卫星数据进行海平面变化研究发现, 1991－2018年波弗特环流区和格陵兰岛近海海域海平面显著上升, 而挪威海近岸海域海平面上升最为明显, 北极海平面整体以1.54 mm/a的速率上升。金波文等[18]利用新奥尔松地区验潮站和GNSS(Global Navigation Satellite System)数据分析得出该区域1993－2018年的绝对海平面变化速率为0.78±0.41 mm/a, 海平面变化存在明显的周期性和季节性。江伟伟等[19]对格陵兰岛近海海域进行相关研究发现该区域1992—2010年海平面变化速率约为1.7 mm/a, 且冰岛附近海域海平面上升速率最高。目前, 高纬地区海平面变化的研究仅局限于北极区域的数据再处理和历史数据的变化分析。本文基于我国首套自主研发的全球海洋气候数据集产品, 在对格陵兰岛近海海域海平面异常数据进行深入分析的基础上, 对比不同预测模型的预测精度, 构建基于小波变换和LSTM网络的WT-LSTM组合模型, 并对该区域2016－2020年海平面变化趋势进行预测。

1 研究区域及数据来源

1.1 研究区域

格陵兰岛近海海域主要由格陵兰海和挪威海组成(60°N～82°N, 45°W～27°E), 其西邻格陵兰岛, 东接欧洲斯堪的纳维亚半岛, 南北分别与北冰洋和北大西洋相接, 如图1所示。该区域是北冰洋的边缘海之一, 同时也是沟通北冰洋和大西洋海水交换的重要通道。受格陵兰寒流和挪威暖流影响, 北冰洋海水流出总量的83%从格陵兰岛东部流出, 流入总量78%的海水从该海域东部流入北冰洋[20]。研究格陵兰岛近海海域的海平面变化规律, 对掌握北冰洋和大西洋海水交换情况及北极气候变化具有重要意义。

图1 研究区域示意图

1.2 数据来源

本文采用的SLA数据来源于自然资源部第一海洋研究所研制的我国首套全球海洋气候数据集(Climate Data Records, CDRs)产品, 该数据集融合了T/P、GFO、ERS-1/2、Jason-1/2、Envisat、Cryosat-2、HY-2A、Saral、Sentinel-3等多颗卫星的测高数据[21-22], 空间分辨率为0.25°×0.25°, 时间分辨率为1个月。由于获取CDRs数据的限制, 本文选取研究区域1993年1月—2015年12月的SLA数据进行分析。

考虑到不同网格对应的实际面积大小会受到不同纬度的影响, 利用式(1)进行网格数据区域加权处理, 进而获取研究区域海平面变化的整体趋势。区域加权处理后的格陵兰岛近海海域1993年1月—2015年12月的SLA时间序列如图2所示, 由图2可以发现, 格陵兰岛近海海域海平面具有明显的季节性变化特征, 每年春季(2—4月)为季节性低海平面期, 秋季(9—11月)为季节性高海平面期, 海平面变化表现出较为明显的上升趋势, 线性趋势约为2.12 mm/a, 低于3.2 mm/a的同期全球海平面变化上升速率[1]。

式(1)中, 表示k时刻的区域加权后的SLA值, 表示网格点位置, 表示k时刻位置的SLA观测值, 表示取样点的纬度。

2 WT-LSTM组合预测模型

由于海平面变化存在不同时间尺度的信号特征, 如年周期、半年周期等, 通过小波变换的原理可知[23], 利用小波函数可分解出一组包含不同周期的海平面变化信号。LSTM神经网络可不需要了解海平面变化的驱动机制实现非线性预测, 但是海平面变化规律较为复杂, 单一的LSTM网络难以学习到不同时间尺度信号的历史规律。因此本文提出一种融合小波变换和LSTM神经网络的组合预测模型, 通过小波变换提取海平面变化的年周期、半年周期和季节内周期等, 并对每个时间尺度的信号建立LSTM预测模型进行海平面变化非线性预测。WT-LSTM组合模型预测流程如下:

(1)小波基与分解层数的确定

目前小波基和分解层深的选择没有确切的标准, 小波基应选择与原信号近似的函数, 使得小波变换后的数据平滑; 分解层数不能太大或太小, 分解层数太大会造成信号的信息损失, 分解层数过少会造成去噪效果不明显, 影响精度。本文小波变换为实现海平面变化趋势的提取, 选用2层分解即可。常用的基小波有Haar小波、db小波、sym小波、bior小波等, db6小波是db小波族中常用的小波之一。由于db6小波分解出的SLA低频信号较为平滑且高频分量的周期与海平面变化存在的主要周期一致, 所以选用db6小波进行2层分解。

(2)离散小波分解

Mallat算法[24]是一种利用低通和高通滤波器划分频带范围, 实现信号的分解与重构的简易算法。本文利用该算法对SLA信号进行离散小波分解, 分解过程如式(2)—(3)所示:

(3)小波系数重构

小波系数长度随分解层数的增加而变短, 因此需对分解的小波系数进行重构, 使得各系数长度与原序列长度相同, 重构算法如式(4)所示。

(4)LSTM模型构建

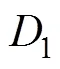
(5)海平面变化预测

WT-LSTM组合模型具体预测流程如图3所示。

图3 WT-LSTM组合模型预测流程

3 实验及结果分析

3.1 评价指标

本文采用均方根误差(root mean square error, RMSE, 记为R)、平均绝对误差(mean absolute error, MAE, 记为MA)、相关系数等评价指标对组合模型预测精度进行评价。R、MA和的计算公式如下[11]:

3.2 WT-LSTM组合预测模型精度分析

为检验本文构建的WT-LSTM组合模型预测精度, 利用文献[11]构建EEMD-LSTM组合模型与WT-LSTM模型进行预测效果对比。分别采用EEMD和WT方法对格陵兰岛近海海域1993—2015年的SLA时间序列进行分解, 再构建LSTM神经网络模型进行海平面变化预测。

EEMD分解时设置高斯白噪声标准偏差为0.4, 加入白噪声次数为100。格陵兰岛近海海域1993年1月—2015年12月的SLA时间序列经EEMD分解后得到7个IMF分量和1个趋势项, 如图4(a)—(h)所示, 由于EEMD分解出的IMF6、IMF7分量未通过95%显著性检验[27], 认为这两个分量是包含物理意义较少的白噪声成分, 在后续利用LSTM网络进行预测时不考虑IMF6、IMF7。经功率谱分析发现IMF1—IMF5分量对应的主要周期分别为3.99个月、11.96个月、11.96个月、55个月、91.67个月。其中3.99个月周期(IMF1)为海平面季节内变化, 11.96个月周期(IMF2、IMF3)为海平面年变化, 55个月周期(IMF4)可能与北大西洋涛动4～5 a的年际振荡有关, 91.67个月周期(IMF5)则与海平面年代际变化相关。由图4(c)、(d)、(e)等可以看出, 虽然EEMD分解可以很好地分离出海平面变化过程中不同时间尺度信号, 但是存在一定程度的模态混叠现象。

图4 1993—2015年格陵兰岛近海海域SLA时间序列EEMD分解结果

图5 1993—2015年格陵兰岛近海海域SLA时间序列小波重构结果

除上述EEMD-LSTM和WT-LSTM两种组合模型之外, 本文还构建了LSTM神经网络模型对研究区域SLA观测值进行直接预测。LSTM、EEMD- LSTM和WT-LSTM三种模型的预测值与相同时间段原始观测值的对比结果如图8所示。从图8中可以看出, LSTM模型预测结果的极值点与真实值相差较大; EEMD-LSTM模型通过分解得到多个时间尺度分量, 再对各分量进行预测, 拟合效果较LSTM模型明显提高; 而WT-LSTM模型的预测结果与观测值最为吻合。三种模型的预测结果均与SLA实际观测值较为吻合, 能够较好地模拟出海平面变化的整体趋势。

图6 EEMD分解各分量预测效果与观测值对比

图7 小波重构各分量预测效果与观测值对比

图8 LSTM、EEMD-LSTM、WT-LSTM模型预测结果对比

表1为LSTM、EEMD-LSTM、WT-LSTM等三种模型2011—2015年预测值与原始观测值的误差统计。从表1可以看出, LSTM模型仅学习了海平面变化的整体趋势, 无法准确把握海平面变化中不同时间尺度的变化信息, 预测结果相对较差。EEMD-LSTM模型精度相对较低, 主要是因为EEMD分解得到的部分IMF分量对海平面变化影响较小, 在预测结果重构时导致误差累积; 其次, EEMD分解结果中存在的模态混叠也会影响预测精度。WT-LSTM模型通过对小波分解得到的主要周期信号进行预测, 很好的把握海平面变化的趋势和周期信号, 同时减少了误差累积, 均方根误差(R)、平均绝对误差(MA)和相关系数()三个指标均表现最为优异。

表1 LSTM、EEMD-LSTM、WT-LSTM模型预测误差比较

3.3 基于WT-LSTM组合模型的2016—2020年格陵兰岛近海海域海平面变化预测

基于上述分析, 本文采用WT-LSTM组合模型对格陵兰岛近海海域2016年1月—2020年12月的海平面变化进行预测, 并与AVISO(Archiving Validation and Interpretation of Satellite Oceanographic)提供的同期实测数据进行比对, 结果如图9所示。图9中黑色实线为研究区域1993年1月—2015年12月的SLA观测值, 红色实线为基于WT-LSTM组合模型的格陵兰岛近海海域2016年1月—2020年12月SLA预测结果, 蓝色虚线为研究区域AVISO同期实测数据。WT-LSTM组合模型预测结果显示1993—2020年格陵兰岛近海海域海平面变化呈持续上升趋势, 线性速率约为2.64 mm/a。基于AVISO网站提供的SLA实测数据得到的该海域1993—2020年海平面上升线性趋势约为2.65±0.49 mm/a。从图9中可以看出, WT-LSTM组合模型预测结果与AVISO实测数据非常吻合, 预测结果较为可靠。

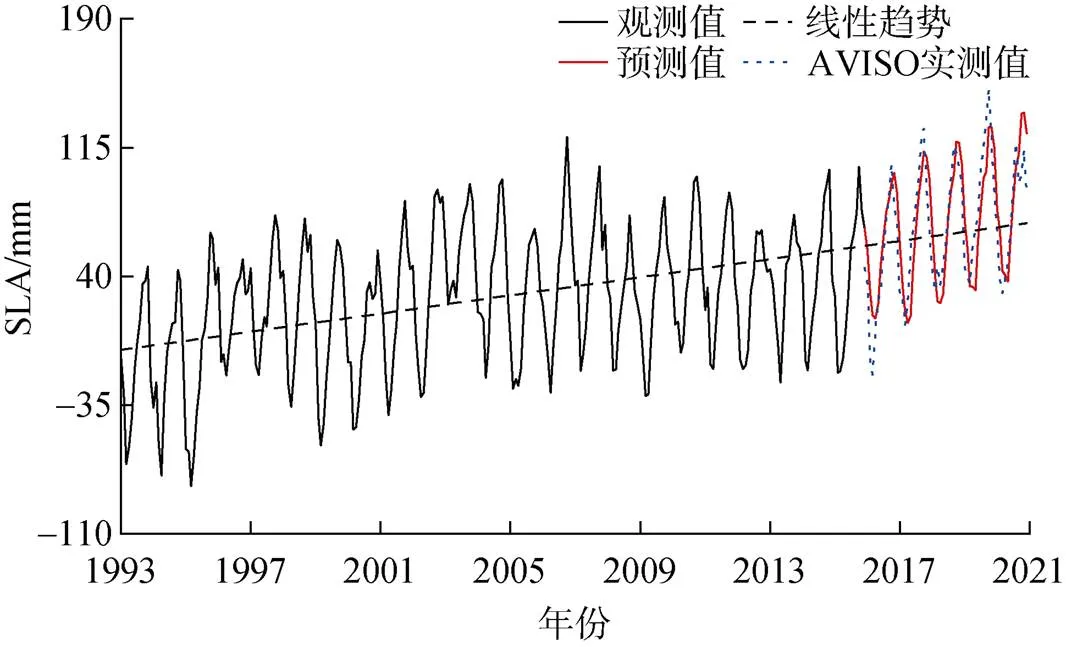
图9 基于WT-LSTM组合模型的格陵兰岛近海海域2016—2020年SLA预测结果与实测数据的比对

4 结论

本文基于我国首套自主研发的海洋CDRs产品, 利用格陵兰岛近海海域1993—2015年的SLA数据, 构建了WT-LSTM组合模型对该区域2016—2020年的海平面变化趋势进行预测, 主要结论为:

(1)WT-LSTM组合模型不仅能够获取海平面变化的整体趋势, 还可提取半年变化、季节变化等海平面变化的细节信息, 从而掌握区域海平面变化中不同时间尺度信号的变化。WT-LSTM组合模型5a期预测的均方根误差(R)和平均绝对误差(MA)分别为12.76 mm和9.94 mm, 均低于LSTM和EEMD-LSTM模型, 表明该组合模型具有较高的预测精度。

(2)基于我国首套海洋CDRs产品中的SLA数据, 利用WT-LSTM组合模型对格陵兰岛近海海域2016—2020年的海平面变化趋势进行了预测, 结果表明该区域海平面变化呈现缓慢上升趋势, 速率约为2.64 mm/a。

(3)WT-LSTM组合模型对海平面变化的极值预测效果相对较差, 且极值预测存在一定的超前和滞后性, 在今后的研究中还需针对极值预测问题展开研究。

(4)由于条件所限, 本文收集到的CDRs产品时间范围相对较短, 仅获取到格陵兰岛近海海域1993—2015年的SLA数据。而基于WT-LSTM组合模型的海平面变化预测是基于历史海平面变化规律对未来海平面变化趋势预测, 如能获取到更长时间范围的SLA数据, WT-LSTM组合模型预测结果会更为准确。

[1] IPCC. Summary for policymakers [M/OL]//IPCC. IPCC special report on the ocean and cryosphere in a changing climate, 2019[2019-11-03]. https: //www.ipcc.ch/srocc/.

[2] 金涛勇, 刘文轩, 姜卫平, 等. 卫星测高确定全球海平面变化研究进展[J]. 测绘地理信息, 2022, 47(3): 1-8.JIN Taoyong, LIU Wenxuan, JIANG Weiping, et al. Research progress on global sea level change determined by satellite altimetry[J]. Journal of Geomatics, 2022, 47(3): 1-8.

[3] 牛余朋, 郭金运, 袁佳佳, 等. 集成奇异谱分析和自回归滑动平均预测日本近海海平面变化[J]. 地球物理学报, 2020, 63(9): 3263-3274. NIU Yupeng, GUO Jinyun, YUAN Jiajia, et al. Prediction of sea level change in Japanese coast using singular spectrum analysis and auto regression moving average[J]. Chinese Journal of Geophysics, 2020, 63(9): 3263-3274.

[4] 孙文, 王庆宾. 基于最小二乘与ARMA组合模型的海平面异常预报[J]. 大地测量与地球动力学, 2012, 32(5): 91-94. SUN Wen, WANG Qingbin. Sea level anomaly forecasting based on combined model of least square and ARMA[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 91-94.

[5] 赵健, 樊彦国, 丁宁. 基于最小二乘与径向基函数神经网络的海平面变化预测[J]. 海洋科学, 2018, 42(5): 92-97. ZHAO Jian, FAN Yanguo, DING Ning. Sea level anomaly forecasting using least square and the radial basis function neural network[J]. Marine Sciences, 2018, 42(5): 92-97.

[6] ZHAO J, FAN Y, MU Y. Sea level prediction in the Yellow Sea from satellite altimetry with a combined Least Squares-Neural Network approach[J]. Marine Geodesy, 2019, 42(4): 344-366.

[7] 顾小丽, 李培良, 谭海涛, 等. 基于RBF神经网络的EMD方法在海平面分析中的应用[J]. 海洋与湖沼, 2009, 40(5): 532-539. GU Xiaoli, LI Peiliang, TAN Haitao, et al. Sea level variation analysis with RBF neural network based EMD method[J]. Oceanologia et Limnologia Sinica, 2009, 40(5): 532-539.

[8] ZHAO J, CAI R, FAN Y. Prediction of sea level nonlinear trends around Shandong Peninsula from satellite altimetry[J]. Sensors, 2019, 19(21): 4770.

[9] 刘进宇, 汪海洪, 欧阳玉华. 基于SSA和ARMA的海平面变化短期预测[J]. 测绘地理信息, 2021, 46(S01): 305-307. LIU Jinyu, WANG Haihong, OUYANG Yuhua. Short-term prediction of sea level change based on SSA and ARMA[J]. Journal of Geomatics, 2021, 6(S1): 305-307.

[10] SHEN Y, GUO J, LIU X, et al. Long-term prediction of polar motion using a combined SSA and ARMA model[J]. Journal of Geodesy, 2018, 92(3): 333-343.

[11] 赵健, 樊彦国, 张音. 基于EEMD-BP组合模型的区域海平面变化多尺度预测[J]. 系统工程理论与实践, 2019, 39(10): 2713-2722. ZHAO Jian, FAN Yanguo, ZHANG Yin. Multi-scale prediction of regional sea level variations based on EEMD-BP combined model[J]. Systems Engineering - Theory & Practice, 2019, 39(10): 2713-2722.

[12] LIU H, HE B, QIN P, et al. Sea level anomaly intelligent inversion model based on LSTM-RBF network[J/OL]. Meteorology and Atmospheric Physics, 2021, 133(2): 245-259.

[13] 张雪薇, 韩震, 郭鑫. 深度学习在海洋信息探测中的应用: 现状与展望[J]. 海洋科学, 2022, 46(2): 145-155.ZHANG Xuewei, HAN Zhen, GUO Xin. Research progress in the application of deep learning to ocean information detection: status and prospect[J]. Marine Sciences, 2022, 46(2): 145-155.

[14] 孙文, 王庆宾, 周睿, 等. 海平面异常序列预报方法的比较与分析[J]. 测绘通报, 2014, 60(1): 46-49. SUN Wen, WANG Qingbin, ZHOU Rui, et al. A comparison and analysis of methods of sea level anomaly time series forecasting[J]. Bulletin of Surveying and Mapping, 2014, 60(1): 46-49.

[15] WU Z, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[16] ZHAO J, CAI R, SUN W. Regional sea level changes prediction integrated with singular spectrum analysis and long-short-term memory network[J]. Advances in Space Research, 2021, 68(11): 4534-4543.

[17] ROSE S K, ANDERSEN O B, PASSARO M, et al. Arctic Ocean sea level record from the complete radar altimetry era: 1991–2018[J]. Remote Sensing, 2019, 11(14): 1672-1701.

[18] 金波文, 王慧, 张建立, 等. 北极新奥尔松地区海平面变化和陆地垂直运动分析[J]. 武汉大学学报: 信息科学版, 2021, 46(4): 503-509. JIN Bowen, WANG Hui, ZHANG Jianli, et al. Sea level change and vertical land motion along Ny-Alesund coast in Arctic[J]. Geomatics and Information Science of Wuhan University, 2021, 46(4): 503-509.

[19] 江伟伟, 李磊, 王春晖, 等. 格陵兰岛附近海域海平面变化的初步研究[J]. 中国海洋大学学报(自然科学版), 2011, 41(10): 10-16. JIANG Weiwei, LI Lei, WANG Chunhui, et al. A preliminary analysis on sea level change in the seas near the Greenland[J]. Periodical of Ocean University of China (Natural Science), 2011, 41(10): 10-16.

[20] 江伟伟. 格陵兰岛附近海域的海平面变化及影响因素研究[D]. 青岛: 中国海洋大学, 2011. JIANG Weiwei. Study on the sea level variations and influence factors in the seas near the Greenland[D]. Qingdao: Ocean University of China, 2011.

[21] 张杰, 孙伟富, 杨俊钢, 等. 海洋气候数据集生成与分析简介[J]. 海洋科学进展, 2019, 37(2): 325-331. ZHANG Jie, SUN Weifu, YANG Jungang, et al. Brief introduction to the first global ocean climate data records (CDRs) of China[J]. Advances in Marine Science, 2019, 37(2), 325–331.

[22] 孙伟富, 张杰, 孟俊敏, 等. 中国南海及邻近海域SST时空分布和变化特征分析[J]. 海洋科学进展, 2018, 36(3): 402-411.SUN Weifu, ZHANG Jie, MENG Junmin, et al. SST analysis of temporal and spatial distribution and change characteristics in the South China Sea and its adjacent waters[J]. Advances in Marine Science, 2018, 36(3): 402-411.

[23] 贺国光, 马寿峰, 李宇. 基于小波分解与重构的时间序列预测法[J]. 自动化学报, 2002, 28(6): 1012-1014. HE Guoguang, MA Shoufeng, LI Yu. A study on forecasting for time series based on wavelet analysis[J]. Acta Automatica Sinica, 2002, 28(6): 1012-1014.

[24] MALLAT S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1989, 11(7): 674-693.

[25] 李亚蒙, 孙宝楠, 丁军航, 等. 基于LSTM的海洋表面短期风速预测研究[J]. 海洋科学, 2022, 46(11): 55-66. LI Yameng, SUN Baonan, DING Junhang, et al. Short-term wind-speed prediction of ocean surface based on LSTM[J]. Marine Sciences, 2022, 46(11): 55-66.

[26] 周玮辰, 韩震, 张雪薇. 基于融合U-Net及ConvLSTM的海面高度异常预报方法研究[J]. 海洋通报, 2021, 40(4): 410-416. ZHOU Weichen, HAN Zhen, ZHANG Xuewei. Research on sea level anomaly prediction based on U-Net structure and ConvLSTM layers[J]. Marine Science Bulletin, 2021, 40(4): 410-416.

[27] WU Z, HUANG N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, 2004, 460(2046): 1597-1611.

Prediction of sea level change based on wavelet transform and LSTM neural network near Greenland

ZHAO Jian, LIU Ren-qiang

(College of Oceanography and Space Informatics, China University of Petroleum (East China), Qingdao 266580, China)

The information on sea-level change data spans several time scales. The traditional prediction methods only fit the trend and periodic terms of sea level change, making it difficult to decompose the signals of different time scales, thereby resulting in low prediction accuracy. This paper proposes a combined prediction model of sea level anomalies based on deep learning prediction models that integrate wavelet transform (WT) and long short-term memory (LSTM) neural networks. Firstly, wavelet decomposition is performed to obtain the low-frequency component reflecting the overall trend of sea level change and the high-frequency component reflecting the main features; each component is then predicted and reconstructed by an LSTM neural network to realize the nonlinear prediction of sea level change. The root mean square error, mean absolute error, and correlation coefficient of sea-level change prediction based on this model are 12.76 mm, 9.94 mm, and 0.937, respectively, and the prediction accuracy is better than that of the LSTM and ensemble empirical mode decomposition–LSTM prediction models. Therefore, WT–LSTM combined model has better application potential for regional sea-level change prediction.

sea level anomaly; wavelet transform; long short-term memory network; sea level change; prediction

Apr. 13, 2022

[The National Key Research and Development Program of China, No. 2016YFA0600102]

P727

A

1000-3096(2023)8-0007-10

10.11759/hykx20220413002

2022-04-13;

2022-10-01

国家重点研发计划项目(2016YFA0600102)

赵健(1981—), 男, 山东齐河人, 博士, 副教授, 主要研究方向为卫星大地测量数据处理, E-mail: zhjianupc@163.com

(本文编辑: 丛培秀)