上行蜂窝网络小区间干扰模型

鞠晓杰，王 雪，王 铎，孔 鑫，周浩天

（中国运载火箭技术研究院，北京 100076）

为有效利用频谱资源，5G、6G 等移动通信系统普遍采用全频率复用技术[1-5]。然而，全频率复用带来了严重的小区间干扰，使得小区边缘服务质量较差。为确保小区边缘具有与小区中心相媲美的服务能力，干扰管理技术已成为学术及工业界研究的热点[6-11]。小区间干扰模型如何既能准确地反映上述因素的影响，又具有较低的复杂度，是研究人员进行干扰管理分析与设计的基础[12-16]。

该文针对全频率复用上行链路，提出基于用户随机位置的干扰模型，该模型中用户随机分布在小区内部，其对相邻小区基站的干扰因子为一个随机变量，并由用户位置及大尺度衰落等因素共同决定。该文提出了等干扰线法，得到了该模型下干扰因子概率密度函数（Probability Density Function,PDF）的闭合表达式，并通过仿真验证了模型的准确性，为后续开展干扰管理设计提供了理论参考。

1 基于用户随机位置的干扰模型

基于用户随机位置的小区间干扰模型如图1 所示，该图选取了蜂窝模型中的两个相邻小区，其中每个小区包含一个位于中心的基站及K个用户。相比于Wyner 模型而言，该干扰模型同样仅考虑相邻小区干扰的影响，非相邻小区由于空间位置相隔较远，所产生的干扰由于路径损耗的影响而被忽略；不同之处在于该模型中K个用户随机分布在小区内部，且不再具有相同的小区间干扰因子，每个用户的小区间干扰因子由用户位置、路径损耗及阴影效应等因素共同决定。此外，该模型中假设小区内部采用理想功率进行控制，即用户根据上行链路情况调整其发射功率，进而保证基站端对该用户的接收功率为固定值，该文假设该固定值被归一化为1。最后，对于距离基站为r的用户而言，其信号由于大尺度衰落而引起的衰减为rμ10ζ/10，其中，μ为路径损耗因子，随机变量ζ由阴影效应引入，服从正态分布，其均值为0，标准差为Y（单位为dB）。

图1 基于用户随机位置的小区间干扰模型

基于上述假设，若用户位置固定，如图1 中的U1，为了保证基站端接收功率为1，U1的发射功率需调整为。此时，U1对于相邻小区基站B2的干扰功率为类似于Wyner 模型，定义干扰因子α为基站端干扰用户与本小区用户信号幅度的比值，则α=，其中，r0、r1分别为用户到本小区基站及相邻小区基站的距离，ζ0、ζ1均服从正态分布，且均值为0，标准差为Y。考虑到ζ0与ζ1由同一用户到不同基站的阴影效应引入，两变量间存在一定的相关性，即ζ0-ζ1服从正态分布，其均值为0，标准差为Y。以上分析可以看出，当用户在小区内随机分布时，干扰因子α为一随机变量，且由用户位置、路径损耗及阴影效应共同决定。

2 无阴影效应情况干扰因子分布

如图2 所示，设定基站B1和B2分别位于(0,0)和(a,0)点，则正六边形小区的边长，每小区所覆盖的面积为Scell=设定小区中某个用户位于(x,y)点，则仅考虑用户随机位置和路径损耗，干扰因子α可表示为：

对式（1）进行化简，可得到：

由式（2）可以看出，当干扰因子α固定时，点(x,y)组成的轨迹为一个圆，其圆心坐标(c,0)和半径r分别为：

由于轨迹圆上的点所对应的干扰因子α相同，因此定义该轨迹圆为“等干扰线”。如图2 所示，等干扰线分为两种类型：“等干扰线1”完全在小区内部，而“等干扰线2”只有部分在小区内部。

由图2 可看出，不同干扰因子的等干扰线为互不相交的圆，且干扰因子小的圆在干扰因子大的圆的内部。利用这一特性，求解干扰因子α概率密度函数（PDF）的基本思想可概括为：对于某个干扰因子α，其对应的等干扰线所包围的面积与小区面积的比值为干扰因子不超过α的概率，即对应α的累积分布函数（CDF），进一步，对该干扰因子的CDF 进行求导便可得到其所对应的PDF。

考虑到“等干扰线2”与六边形小区边缘有多种不同的相交方式，需要对不同的相交方式进行分段处理，其复杂度相对较高。为此，理论分析中考虑等效的圆小区模型，如图3 所示，其中基站位置及圆小区面积均与图2 相同，则圆小区的半径为对于等效的圆小区模型，若等干扰线与小区边缘相切，则r-c=R，进一步化简可得到干扰因子α=0.587μ。

图3 等效圆小区情况的等干扰线示意图

因此，当α≤0.587μ时，等干扰线完全在小区内部；反之，等干扰线仅有部分在小区内部。

2.1 等干扰线完全在小区内部情况

等干扰线完全在小区内部，即α≤0.587μ，对于某个干扰因子α，其等干扰线所包围的面积对应图3中的阴影部分，且S=πr2，则α的CDF为Fα(α)=对Fα(α)求导可得到α的PDF 为：

2.2 等干扰线部分在小区内部情况

如图4 所示，对于等干扰线部分在小区内部的情况，即α＞0.587μ，此时等干扰线与小区边缘的交点E 坐标可表示为：

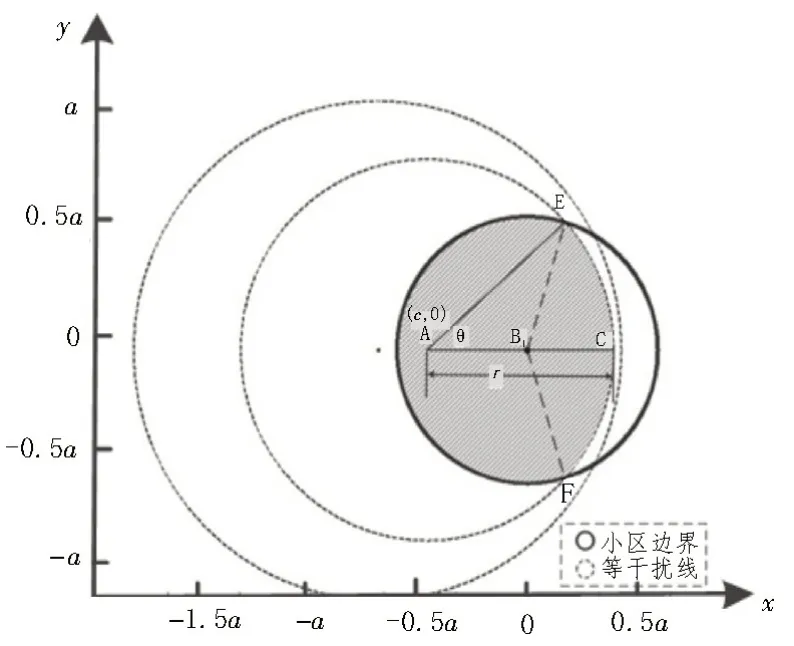
图4 等干扰线部分在小区内部示意图

该情况下，等干扰线包围的面积如图4 中的阴影部分所示，该文利用“微分”思想求解干扰因子由α变化为α+dα时（其中，dα为一阶无穷小量），等干扰线所包围面积的变化程度。

如图5 所示，当干扰因子由α变为α+dα时，等干扰线轨迹圆的圆心由A 点移动到B 点，其半径由r变为r+dr。此时，干扰线包围面积的变化即图5 中的阴影部分。需要注意的是当干扰因子增加一阶无穷小量dα时，等干扰线包围面积的变化非常小，图5仅为了直观地反映面积变化。

图5 阴影面积求解示意图

对于图5 中阴影部分的面积，可通过点A、G、H组成的面积减去点A、E、F 组成的小扇形面积得到。对于小扇形而言，其半径为r；但是对于AGH组成的图形而言，由于轨迹圆圆心的移动，半径在不同的角度φ取值不同，如当φ=0 时，其半径为dAD=r+dr-|dc|，其中，| dc|为圆心移动的距离。相应地，角度φ对应的半径为r+dr-|dc|cosφ。为简化分析，将AGH 组成的图形近视为扇形，其平均半径r～ 可表示为：

因此，图5 中阴影部分的面积可表示为：

注意式（7）中忽略了高阶无穷小量的影响。因此，干扰因子α的PDF 可表示为：

其中，dr/dα和dc/dα分别为式（3）中r与c的导数。至此，得到仅考虑路径损耗及用户随机位置情况下干扰因子α的PDF，可表示为如下的分段函数：

3 有阴影效应干扰因子分布

当考虑阴影效应时，干扰因子可表示为αsh=α10ζ/20，其中，α的PDF 如式（9）所示，ζ服从正态分布，其均值为0，标准差为Y。

由于α与ζ相互独立，则lg 与ζ/20 相互独立。根据两个独立随机变量和的PDF 公式，可以得到lg(αsh)的PDF 为：

其中，符号“*”表示卷积运算。

4 仿真及数值分析

通过蒙特卡洛仿真和理论分析的方法分别得到无阴影效应及有阴影效应两种情况下，用户随机位置干扰模型中干扰因子的PDF 曲线，以验证分析方法的有效性，分析路径损耗及阴影效应如何影响干扰因子的分布。

用户随机位置干扰模型下，小区间干扰因子是由用户位置及大尺度衰落共同决定的随机变量。分别通过蒙特卡洛仿真及理论分析方法得到干扰因子的分布。考虑到某些参数下，干扰因子可能很小，该节采用对数坐标，即给出lgα的PDF 曲线，使仿真及理论结果对比更为明显。

对于蒙特卡洛仿真而言，从蜂窝系统中选取两个相邻的小区，如图1 所示，其执行过程如下：首先，在小区1 中随机设定参考用户的位置，则可得到该用户对基站2 的小区间干扰因子α，并相应地得到lgα。将上述过程重复2 000 次，并通过统计的方式得到lgα的PDF 曲线。对于理论分析而言，无阴影效应及有阴影效应情况下，lgα的PDF 分别如式（9）和式（10）所示。

4.1 不考虑阴影效应情况干扰因子分布

图6 给出无阴影效应情况下，lgα在不同路径损耗因子μ下的理论及仿真PDF 曲线，其中蒙特卡洛仿真对应两个相邻的六边形小区。从图中可看出，当路径损耗因子μ从2.0 增加到5.0 时，仿真及理论PDF 曲线均向左移动，这意味着当μ增加时，小区间干扰减弱。由此得到启示：可利用路径损耗效应来对抗小区间干扰。此外，对比仿真及理论PDF 曲线，可以看到除了部分lgα的取值外，理论与仿真曲线吻合较好。对于理论与仿真不吻合的部分，其主要原因在于理论分析中为了简化，采用等面积的圆小区来代替六边形小区。这种处理方法在小区内部较为准确，但对于六边形小区的边缘部分，圆小区无法对其进行刻画。为了验证这一论断，在图7 中将仿真场景设为两个相邻的等面积圆小区，可以看到图6中不吻合的点在图7 吻合得很好。

图6 lg α 理论及仿真PDF曲线（六边形小区）

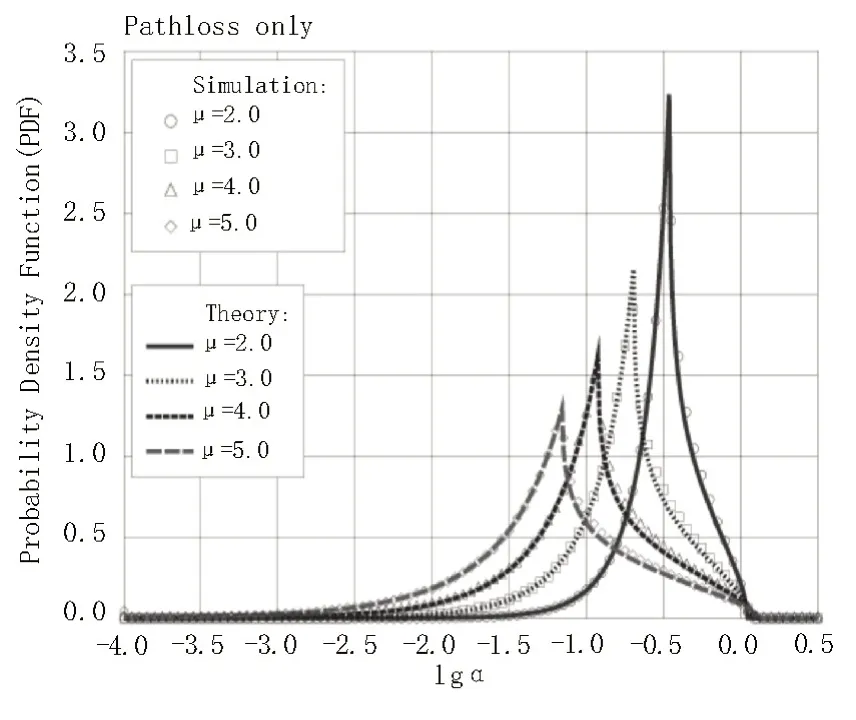
图7 lg α 理论及仿真PDF曲线（圆形小区）

4.2 考虑阴影效应情况干扰因子分布

图8 给出考虑阴影效应情况下，不同路径损耗因子所对应的lgα仿真及理论PDF 曲线。其中，阴影效应参数γ设为8 dB，以满足城市蜂窝系统的需要。此外，仿真所针对的系统模型与图6 相同，均为两个相邻的六边形小区。由图可知，类似于图6 的结论，即当路径损耗因子增加时，小区间干扰随之减弱。此外，对比理论及仿真PDF 曲线可看出，二者吻合得很好，即使对于某些小区边缘的lgα，也未出现图6 中的不匹配情况。由此可得出，相比于路径损耗而言，阴影效应对lgα的分布起主导作用，使其分布形状更接近于式（10）中ζ/20 的分布，即正态分布。最后，需要指出的是，当考虑阴影效应时，干扰因子可能超过1，即lgα＞0，这意味着相邻小区干扰信号的强度可能超过本小区用户。

5 结论

该文提出基于用户随机位置的小区间干扰模型。该模型下，小区间干扰因子是由用户位置、路径损耗及阴影效应等共同决定的随机变量。利用等干扰线分析方法，该文给出无阴影效应和考虑阴影效应两种情况下干扰因子概率密度函数的闭合表达式，并通过仿真验证了理论分析的准确性。分析表明，小区间干扰随着路径损耗因子的增加而减小，且阴影效应在干扰模型中占据主导地位，为后续开展小区间干扰管理设计提供参考。