基于MSP432 的波形分析及显示系统设计

王国庆，甄喆，袁毅，杨会龙，孙艳丽

（海军航空大学，山东烟台 264001）

目前测量波形失真度的仪器按原理主要分为基于基波抑制法的模拟式和基于频谱分析法的数字式[1]。二者各有特点，其中基波抑制法对200 kHz 以内波形测试准确度较高，成本较低，但测试失真范围和频率范围较窄，而且无法重构并显示波形；基于频谱分析法因需对信号进行模数转换（ADC），频率较高的信号测试精度受限于AD 采样的上限频率，误差也与量化、采样间隔的非均匀、非整周期采样导致频谱泄露等有关，且仪器价格昂贵[2]。针对以上信号失真度测量方法一种优缺点，该文设计一种基于MSP432 的波形分析及显示系统。该系统采用频谱分析法，利用MSP432 自带ADC 具有高采样率、高精度优势，借助Matlab 仿真通过取前后多个值的均方根提高幅值精度，并根据频率改变采样率，减少非整周期采样导致频谱泄露，从而实现对任意周期信号的各谐波分量幅值进行高精度测量，计算失真度并重构波形进行显示。

1 系统硬件设计

系统硬件结构主要包括MSP432 微处理器、模数转换器（ADC）、电平转换电路及滞回电压比较器等部分。电平转换电路将输入信号电压转换成ADC支持的0～3.3 V 电压，ADC 将待测试的模拟信号转变成微处理器识别的数字信号，MSP432 微处理器主要进行FFT 变换、基波分量查找、谐波分量幅值计算，失真度计算及波形重构。滞回电压比较器将输入信号转换成方波，由处理器进行频率粗测量。

1.1 微处理器及模数转换器

以MSP432P401R 微控器作为系统的主控与数据处理核心，允许最多32 个独立的ADC 通道进行转换并支持16 位量化（文中采用14 位量化），采样精确度高，采用FFT 进行数据处理。同时MSP432 单片机的ADC 采样时钟由单片机内部的48 MHz 时钟分频得到，分频系数是48、49、50 等整数，因此分频系数为48 时有最高的采样频率1 MHz，基本满足100 kHz 高频率信号及其2、3、4、5 次谐波信号的采样要求，可以采集幅度调理后的待分析波形信号。MSP432P401R 微控器自带8 路串口，可以与计算机和迪文屏通信。

1.2 电平转换电路

在输入信号电压峰峰值范围10～600 mV，基波频率为10 Hz～100 kHz 条件下，需要考虑MSP432 内部ADC 的测量信号单极性的特点和运算放大器的带宽限制。由于该单片机集成的ADC 只能支持输入0～3.3 V 电压[3-6]，因此需要在单片机之前加上放大电路和上拉电路，其目的就是将小幅度信号放大并把信号源输出的双极性信号变为单极性信号，确保MSP432 内部ADC 正常工作。选择带宽较大的AD8055AR 运算放大器，并通过设计负反馈环节展宽电路带宽及提升带负载能力[7-8]。仿真电路如图1所示。

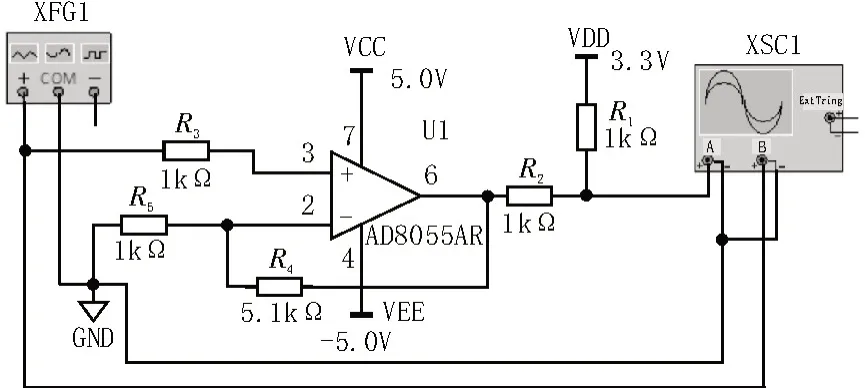
图1 电平转换仿真电路

集成运放的输出电压（AD8055AR 的6 脚）为Uo1与输入电压Ui（XFG1 的输出端+）关系为：

运算放大后增加了一个电压抬升电路，通过电压源UDD与R1、R2组成的分压电路与Uo1叠加，把信号的电压抬升至Uo（XSC1 的A 端），保证其在ADC 合理范围之内，从而实现正常测量。送至MSP432 内部ADC 的电压Uo为：

在模数转换完成后去掉抬高电平所用的直流分量，即可通过FFT 进行解算。

1.3 ADC处理

ADC 处理给后续的FFT 处理提供原始数据[9-11]。MSP432 内部带4 点数的FFT 函数，该文在单次波形分析时，选择处理1024 点连续采样的数据。

当输入信号频率1 kHz，采样率为2、4、8、16、32、64、128、256、512 kHz 时，取1 024 个采样点做FFT时，这1 024 个采样点正好对应着整数个周期的输入信号，这种采样率与频率之间的关系，经过FFT 后，其基波及2、3、4、5 次谐波的位置比较准确，THD 的计算值也比较准确，但输入信号频率越高，采样率如果不能相应地增高，误差就会变大，因非整周期采样导致频谱泄露，经过FFT 后，基波与2、3、4、5 次谐波的位置与理论上的位置有偏差。

为了减小频谱泄露导致的误差，采取了两种措施：1）取测量的基波和谐波位置的前后2 个点，共5 个点求其均方根作为该频点的幅度，再利用失真度计算公式计算失真度；2）根据基波频率，选择较合适的采样率，尽量减少由于非整周期采样导致的频谱泄露，这个过程需要额外测量出基波信号频率。测量基波信号频率可采用两种方法：一种是用滞回比较器形成方波，再将方波接入单片机的数字口，用定时器设定时间，然后计算设定时间内方波的个数来换算出基波频率；另一种方法是直接用640 kHz 采样时钟采集输入信号，粗略计算基波频率。

1.4 滞回电压比较器电路

滞回比较器采用集成运放构成正反馈电路，通过与门限电压1.65 V 进行比较，将输入信号整形为方波信号，电路图如图2 所示。通过MSP432粗测该方波信号频率，从而选择合适的采样率能够获得整数个周期信号，减少频谱泄露[12-13]。同时还为FFT 变换后找到基波峰值及谐波分量峰值作参考，起到加快算法寻找基波与谐波峰值的辅助作用。

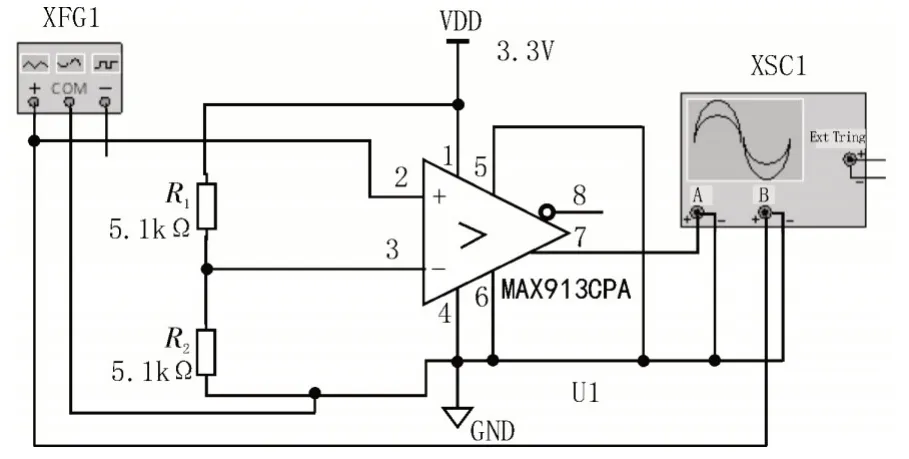
图2 电压比较器仿真电路

2 系统软件实现

2.1 波形分析软件实现

系统的信号采集、波形分析与数据显示模块基于MSP432 开发板和迪文屏开发实现，软件工程文件由keil 开发环境编写[14-16]。在keil 工程文件中，ADC、串口等都有例程。在配置ADC函数时，先设置分频系数，用48 MHz 除以该分频系数得到不同的采样率（例如设置分频系数为750时，得到采样率为64 kHz），再设置每采集1 024 个数据点产生一次中断，进行数据读取与分析。在配置串口函数时，设置各个串口前置分频器系数为26，使MSP432 单片机与计算机、迪文屏的串行波特率均为115 200 bps。

在main.c 函数中依流程进行如下操作：根据迪文屏输出的数据协议，与迪文屏实时通信，响应迪文屏按键命令；响应ADC 数据准备好中断，得到1 024点待分析数据；利用MSP432 自带的FFT 库函数，计算待分析数据的基频以及2、3、4、5 次谐波幅度，得到待分析数据的基频和谐波频率位置坐标；根据基频和谐波频率位置坐标计算失真度、用计算出的各次谐波幅度，乘以理想的点频信号，叠加后重构待分析波形；将失真度等结果数据、原始波形以及重构波形等送迪文屏显示；程序调试过程中的测试数据通过串口送计算机等[17-18]。流程如图3 所示。

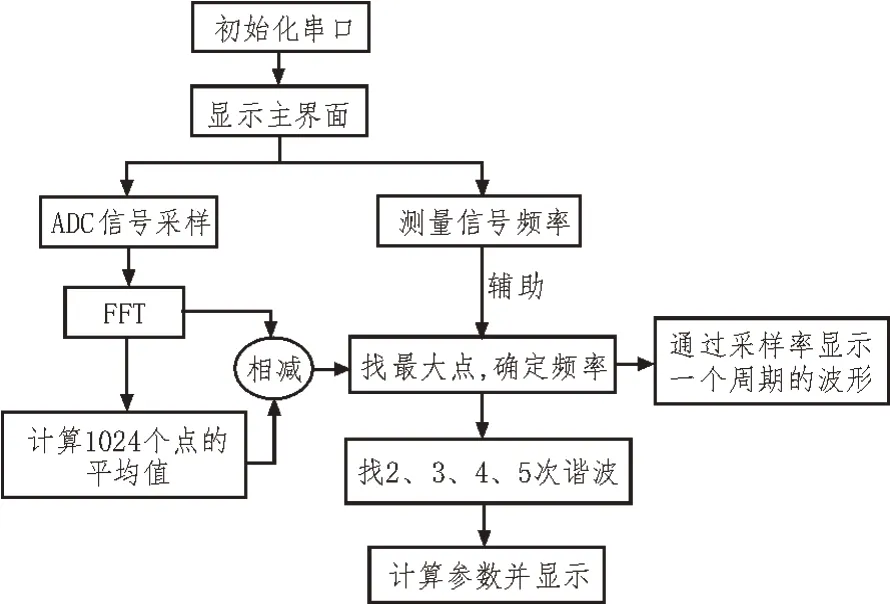
图3 软件流程图

由于输入信号频率范围为10 Hz～100 kHz，并且采样率要不低于基波信号频率的10 倍，所以设计时，需要分段设置采样率。在改变信号频率和谐波参数时，可以通过在触摸屏上设置按键来实现。在程序调试过程中，利用串口将不同节点的数据传送给计算机，通过Matlab 软件读取数据，验证每一步是否正确。

2.2 显示部分软件实现

迪文屏也配有专门的上位机开发软件DGUS Tool V7.388，该软件设计用到“按钮返回”、“数据变量显示”、“动态曲线显示”等功能，“按钮返回”需要配置键值和变量地址，选择数据自动上传，配置完成后，点击此处按钮屏幕发送响应指令；“动态曲线显示”功能稍微复杂，该设计专门编写了动态曲线显示函数，需要用到波形曲线数据，通道号、数据长度等参数，其中波形曲线数据用无符号16 位二进制数表示，占两个字节，通道号、数据长度用无符号8 位表示，占一个字节。该设计中设置一个波形的总点数为180 点，而每个数据占用两个字节，即一个波形的总点数占用360 字节，由于360 大于255，因此无法用一个无符号8 位来表示一个波形所占用的总字节数，在发送180 点波形数据时，分两次发送，第一次发送100 点，发送时先向迪文屏发送16 进制指令，再发送200个字节的波形数据。第二次发送80点，发送时先向迪文屏发送16 进制指令，再发送80 个字节的波形数据。

在波形重构方面，基本思路：不管波形的基波频率是多少，都要在迪文屏上显示基波一个周期的完整时域波形。相应地，为了显示比例一致，也要在迪文屏上显示2 次谐波两个周期的完整时域波形、3次谐波3 个周期的完整时域波形、4 次谐波4 个周期的完整时域波形以及5 次谐波5 个周期的完整时域波形。因此需要先在程序中存储1-5 次谐波波形变量，每个变量180 点，对应着1-5 个周期的正弦波形，均由Matlab 程序生成。当计算出各次谐波系数后，用谐波系数加权相应的谐波波形变量，最后叠加在一起，完成重构波形，并送迪文屏显示[17-18]。

3 系统测试

3.1 Matlab仿真结果

通过Matlab 软件模拟基波频率、谐波幅度，设置采样率，仿真基波和谐波的时域波形，用自带的FFT函数计算信号的频谱，排除直流分量后，用最大值函数找到了基波位置和幅度，并根据基波的位置预测2、3、4、5 次谐波的位置，找出其波形各谐波分量的电压有效值，如图4 所示。进而利用式（3）进行相关计算，最终输出信号失真度。在Matlab 中对失真度标称值THD0进行求解并记录结果。

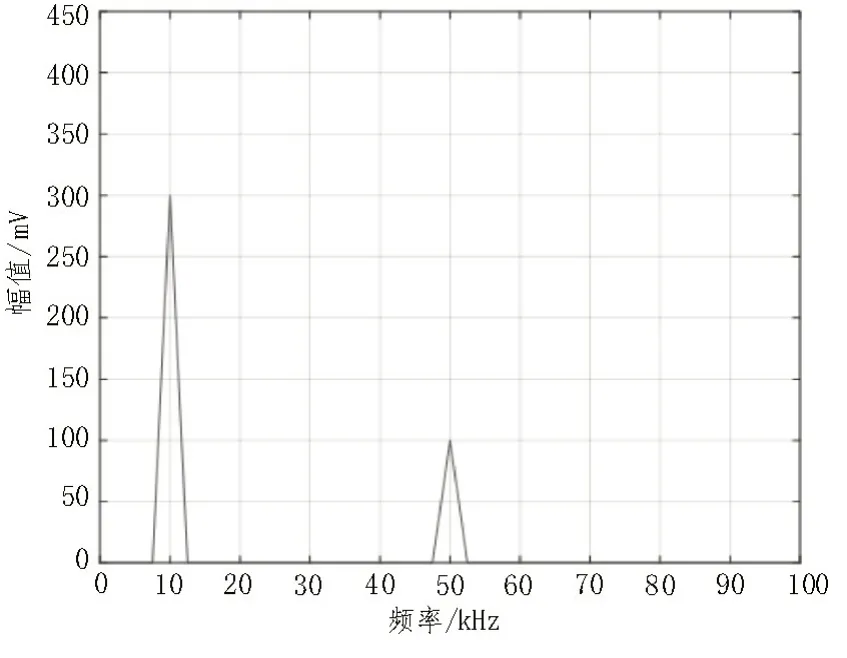
图4 信号基波及谐波分量位置仿真

3.2 实测数据分析

将设计的外围电路与MSP432P401R 开发板及迪文屏进行连接如图5 所示，信号源分别设置基波、多次谐波的频率与幅值，产生的信号作为系统的输入信号，输出接到迪文液晶屏，多次改变基波、多次谐波的频率与幅值，记录显示结果并与Matlab 仿真结果比较，如表1 所示。

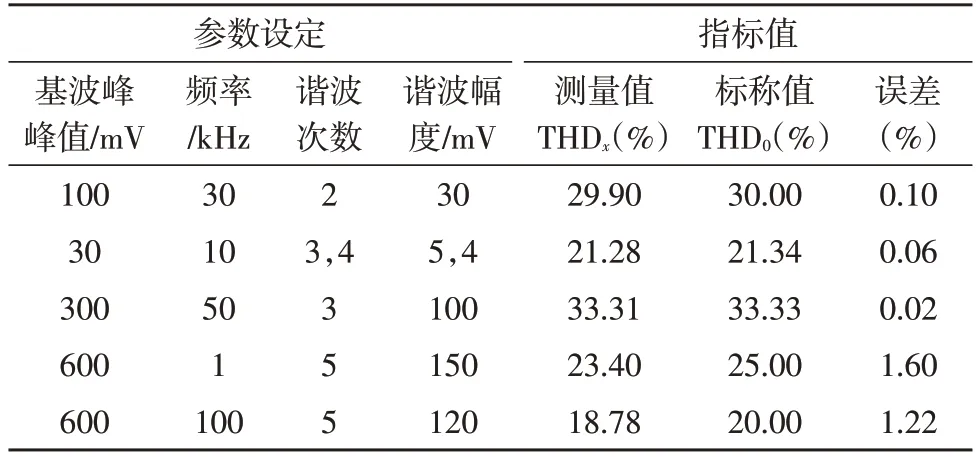
表1 输入谐波信号的MSP432实测谐波失真率

图5 液晶显示波形及失真度

根据实测结果可知，基于MSP432 的波形分析及量示系统实测值与Matlab 仿真结果接近，误差很小，说明该系统能以较高的精度测量信号的谐波分量及失真度。

4 结束语

该文设计的波形分析及显示系统可以实现电压范围10～600 mV，基波频率10 Hz～100 kHz 的5 次内谐波值及失真度值测量与计算，且能够重构波形。对电压大于600 mV 的信号可使用电压衰减电路处理后再输入该系统。此外，该文所提的波形重构及针对频谱泄露进行采样分段可为失真度测量提供有益参考。