非典型边界轴向移动绳的行波解及振动抑制

2023-11-20贺钰腾陈恩伟吴远峰任雪倩陆益民

振动工程学报 2023年5期

贺钰腾，陈恩伟，吴远峰，任雪倩，陆益民

（合肥工业大学机械工程学院，安徽合肥 230009）

引言

缆车、带锯、电梯、涂装机械、流体管道等工程都涉及到轴向移动系统，移动材料所产生的振动会影响设备正常运行。作为一种轴向移动系统模型，轴向移动绳系统的振动研究以及振动控制具有重要的意义。

轴向移动绳系统横向振动的解析计算方法主要有摄动法、模态分析法［1］、行波法等。Wickert 等［2］利用模态分析和格林函数方法推导出移动绳模型振动响应的精确表达，指出移动载荷作用下的轴向移动绳振动响应由三个行波组成，为本文的受迫振动求解提供了思路。Lee 等［3］研究了不同边界条件对轴向移动绳系统固有频率及能量变化的影响。Tan等［4］利用传递函数法获得具有一般边界的移动绳精确解，基于波动理论分析其动力特性。Yang 等［5-6］基于不变流形法推导出轴向移动材料的线性和非线性复模态方程。Lu 等［7-8］研究了轴向移动绳系统在时变边界条件下的节点和共振规律。Gaiko 等［9］研究了移动绳在不同边界条件下的反射波，获得了半无限长移动绳振动响应的精确解。Chen 等［10-14］将行波法应用于有限长绳移系统，考虑到行波在左右边界会发生多次反射，提出了一种适用于各种类型边界的行波反射叠加法。本文基于此理论，将轴向移动绳系统的行波解拓展到多周期以及受迫振动中。

与分布式控制相比，轴向移动绳系统的边界控制方法更加简单［15-16］。Lee 等［15］根据速度反馈在轴向移动绳系统边界处施加阻尼力，并利用李雅普诺夫方法证明其稳定性。Kelleche 等［17］利用边界低增益自适应输出反馈控制使非线性轴向移动结构达到指数稳定。Nguyen 等［18］在边界处设置阻尼器和液压控制器，并考虑边界处质量，利用李雅普诺夫方法得出了稳健的边界控制和自适应规律。Fung 等［16］基于输出反馈法和极值原理，开发了一种用于边界处有质量阻尼的移动绳的最优边界控制器。何修宇［19］、许冰霜［20］、刘屿等［21］运用李雅普诺夫直接法对轴向移动系统进行分析，证明了所设计的边界控制策略能够使系统的横向振动逐渐变小并趋于稳定。

以上研究大部分针对绳移系统的自由振动，所提出的边界控制方法是否适用于存在外界激励的情况有待验证。本文针对此问题，研究均布简谐载荷作用下的轴向移动绳系统，在边界处设置的质量-阻尼-弹簧控制器和力执行器可以抽象为非典型边界，利用绳子边界处的状态设计边界控制力，运用行波反射叠加法精确求解其真实响应，验证控制方法的有效性。考虑了绳移系统受均布简谐激励力时的边界控制问题。

本文第1 节建立具有非典型（质量-阻尼-弹簧）边界的轴向移动绳系统模型；第2 节使用行波法对所建立的数学模型进行求解；第3节寻求最优边界控制力；第4节对边界振动控制效果进行仿真；第5节为结论。

1 运动方程和边界值问题

本文研究的轴向移动绳系统如图1 所示，左端为固定边界，右端控制器可化简为质量-阻尼-弹簧边界，执行器可化简为力f作用在边界处，x为固定的轴向坐标，u为横向位移函数，u（x，t）表示轴向移动绳在t时刻x处的横向位移，l0为两边界之间绳子的长度，常数v为绳子的轴向移速，ρ为绳子线密度，P为绳子中张力，η为右边界处的黏性阻尼系数，k为右边界处弹簧的刚度系数，m为右边界处的质量。

图1 具有质量-阻尼-弹簧边界的轴向移动绳系统Fig.1 An axially moving string with mass-dashpot-spring boundary

绳子所受均布简谐载荷集度为Asin(ωt) N/m，由于此为变质量系统，根据修订过的哈密顿原理［22］求得运动控制方程：

推导过程参见附录A。其中，u的下标表示对其求偏导，c=表示波速。初始条件设为：

式中ϕ(x)与ψ(x)分别表示轴向移动绳系统的初始位移与初始速度。

2 行波法求解

轴向移动绳系统自由振动可以分解为两个左右行波［23］，当系统受均布简谐激励力时，运动方程式（1）的通解可写为：

式中F(x-vrt)表示速度为vr=c+v的右行波；G(x+vlt)表示速度为vl=c-v的左行波；Q（t）为受激励力影响的关于时间的函数，因为激励力是均布的，所以Q与坐标x无关。

将式（5）代入式（1）并求解可得：

式中ω表示简谐载荷的角频率。

C1与C2的取值并不影响最终横向响应的求解结果，不妨令式（6）中任意常数C1=C2=0，可得：

将通解（5）代入到初始条件（4）可得：

对式（8）求解可得：

这里的x1为任意常数，并不影响最后振动响应的求解结果，不妨令x1=0。

将通解式（5）代入边界条件（2）和（3）可得：

由式（11）可求解G（s）。式（11）的特征方程为：

二阶常系数非齐次微分方程（11）的解根据β的取值不同可以分为两种情况：β≠1 与β=1。当β≠1时，方程（11）的解为：

式中a为某一常数；C3和C4表示任意常数。

β=1 时的求解过程与β≠1 时类似，考虑到理论的完整性，β=1 的情况见附录B。

根据行波反射过程［13］可知，在第n个行波周期期间，左行波G2由初始右行波F1在右边界反射而来：

其中，上标n表示行波所在的行波反射周期数，行波反射周期为T=；一个周期内，行波每经过一次，反射下标数字加1（一个周期内，初始左行波为G1，最后一次反射所得的左行波为G3），更详细的行波反射说明参见文献［13］。

连续性条件为：

将式（15）代入到式（16）可得：

同理可得，在第n个行波周期ta（ta=时刻之后，左行波G3由右行波F2在右边界反射而来，ta为右行波由绳左端点移动到右端点的时间，详细定义参见文献［13］。

连续性条件为：

式（15）和（18）为右侧边界的反射方程。

根据式（2）中的左侧固定边界条件易得左侧边界反射方程为：

当轴向移动绳系统进行自由振动时，由文献［13］可知，以行波表示的振动能量公式为：

3 振动抑制

根据第2 节，当已知非典型边界的轴向移动绳系统的初始条件时，可以求得其真实的振动响应和自由振动能量，这对于系统的振动抑制具有指导意义，同时能够体现边界控制对振动抑制的效果。工程实际应用中，在边界处安装传感器、控制器和执行器，传感器用于获取边界处的位移、速度等参数，执行器根据传感器获取的数据进行力控制。振动抑制的目的是通过改变边界条件，使得一个行波反射周期后的轴向移动绳系统在无激励时不再有横向振动，在受激励力时能快速稳定且减小振幅。

当执行器的控制力满足：

时，控制力抵消了边界质量、弹簧刚度的影响，调整边界阻尼到最优值［15］如下：

此时，右边界条件为：

右边界行波反射方程为：

可见右边界的反射波没有横向振动。

4 仿真算例

仿真使用的初始条件为：

式中A0与B0分别表示初始位移与初始速度的最大值。

表1 展示了仿真所用到的基本参数，其他数据均可由这些基本参数求得。

表1 仿真所选用的参数Tab.1 Parameters chosen for the simulation

4.1 无激励力

无激励力时，A=0。当有边界控制时，边界控制方法是在右边界处安装可以抽象为质量、阻尼、刚度和力的控制器和执行器，进而改变边界条件，当执行器采用如式（24）所示的控制规律时，此时右边界等价于采用最优阻尼控制的边界；当没有边界控制时，右边界处不安装控制器和执行器，右边界处没有任何力和约束，右边界条件（3）变为：

此即自由边界条件（非边界控制）。

图2（a）～（d）分别展示了前5 个行波反射周期，轴向移动绳系统在不同位置处的横向位移响应。以图2（b）为例，纵坐标u（0.5l0，t）/m 表示移动绳在中点处的位移，单位是米，横坐标t/T为周期数。通过图2 可以看出，一个行波反射周期后，合适的边界控制对于轴向移动绳的横向振动抑制尤为明显。

图2 有无边界控制的位移响应比较（无激励力）Fig.2 Comparison of displacement response between boundary control and non-boundary control（without excitation）

图3（a）展示了轴向移动绳系统前5 个行波反射周期的总能量变化情况，纵坐标E/E（0）表示移动绳的总能量除以初始能量，为无量纲坐标。从能量的变化幅度可知，总能量中轴向动能占比很大，经过一个行波反射周期后，受最优边界控制的移动绳将不再有横向振动，只剩下轴向动能=0.9993。通过边界控制将边界条件转化为最优阻尼边界，使得轴向移动绳系统在一段时间后不再振动，结果与文献［15］的一致，验证了本文结果的正确性。图3（b）和（c）进一步展示了左右行波的能量变化，纵坐标同样经过无量纲化，EF表示式（23）中的右行波能量，EG表示式（23）中的左行波能量。从以上的能量变化同样可以看出，合适的边界控制有利于轴向移动绳的横向振动抑制。

图3 有无边界控制的能量变化比较（无激励力）Fig.3 Comparison of energy variation of boundary control and non-boundary control（without excitation）

4.2 均布简谐激励力

本小节在移动绳受均布简谐激励条件下，将有边界控制和无边界控制的两种情况进行对比。

首先，研究没有边界控制时的共振现象，由文献［3］可知，固定-自由边界轴向移动绳系统的K（正整数K=1，2，3，…）阶固有频率ωK为：

根据表1 所给参数，计算出ω1=4.35 rad/s，ω2=13.05 rad/s。

取均布简谐激励力幅值A=0.01 N/m。图4（a）～（d）分别展示了不同频率激励时，固定-自由边界轴向移动绳系统前10 个周期内的横向位移响应，X轴坐标x/l0为无量纲空间坐标；Y轴坐标t/T为无量纲时间；Z轴坐标u(x，t)/m 表示对应轴向位置处的横向位移，单位是米。

图4 不同激励频率作用时的位移响应Fig.4 Displacement response for different excitation frequencies

可以看出对于轴向移动系统，当均布简谐载荷的频率为一阶共振频率ω1（4.35 rad/s）时，系统发生共振，之后随着共振频率的增加，系统的振动幅值减小。值得注意的是在图4（d）中，当均布简谐激励的频率为系统的二阶固有频率时共振并不会发生，这种非共振现象是由系统的轴向移动引起的。轴向移动绳系统是一种变质量系统，绳子在边界处的流入与流出影响控制体能量的变化率［24］。

其次，就轴向移动绳系统发生共振的情况（ω=ω1），采用边界控制的方法抑制其横向振动。当轴向移动绳系统受均布简谐载荷Asin(ωt)作用时，经过式（24）的力控制，右边界反射方程最终变为式（27）。

图5（a）～（d）分别展示了前10 个行波反射周期内，轴向移动绳系统受频率为ω1的均布简谐载荷激励时，不同位置处的横向位移响应。可以看出，在轴向移动绳系统所受均布简谐载荷的频率为一阶共振频率时，系统发生共振，本文提出的边界控制方法依然可以明显降低系统的振动幅值，振动抑制效果明显。

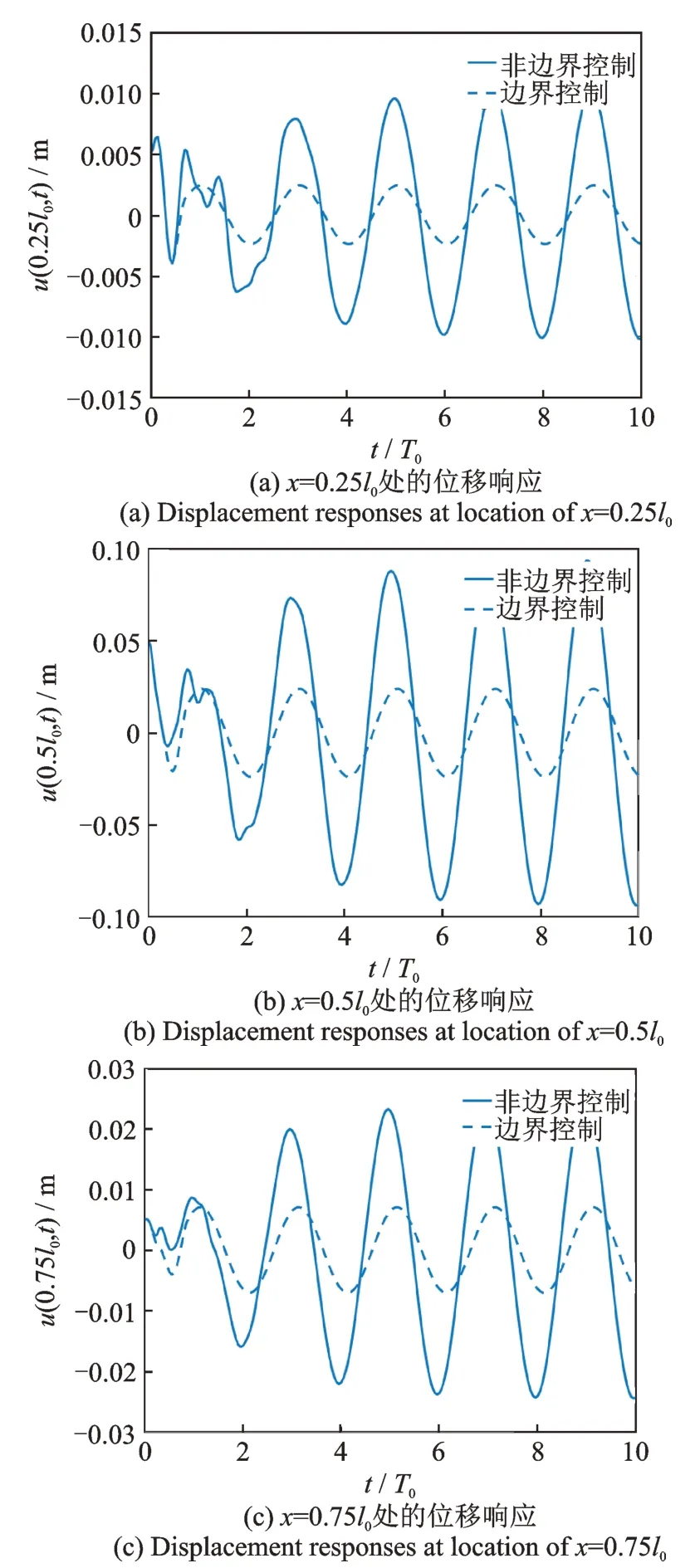
图5 有无边界控制的位移响应比较（受均布简谐激励力，频率ω=ω1，幅值A=0.01 N/m）Fig.5 Comparison of displacement response between boundary control and non-boundary control（subject to the uniform harmonic force with frequency ω= ω1 and amplitude A=0.01 N/m）