基于ACVMD-WT 法的GNSS-RTK 高耸结构动态监测与模态分析

2023-11-20熊春宝史青法

振动工程学报 2023年5期

熊春宝，王猛，尚智，史青法

（1.天津大学建筑工程学院，天津 300350；2.天津市陆海测绘有限公司，天津 300304）

引言

中国在基础设施发展方面取得了重大成就，以台北101 大厦、广州塔、天津117 大厦为代表的超高层或高耸结构，在人们的生产、生活等方面扮演着重要角色。然而，风荷载、地震荷载、温度及结构自身等因素会导致其发生变形甚至倒塌。因此，迫切需要对建设时间相对久远的建筑结构进行动态监测以保证其功能的正常使用。

现阶段，各类监测传感器已应用到结构监测中，如加速度计［1］、三维激光扫描仪［2］、雷达干涉系统［3］、摄影技术［4］以及全球导航卫星系统［5］等。但是加速度计在数据积分过程中会产生“漂移”现象；三维激光扫描技术对外部环境要求相对较高；雷达干涉测量同样对大气条件要求相对苛刻；摄影测量的自身硬件水平、光照强度等都会影响成像质量。

全球导航卫星系统（Global Navigation Satellite System，GNSS）具有操作简单，受外部条件制约性小，效率高等优点，能够实现对目标进行全天候的连续实时监测［6］。梁强武等［7］利用GPS 和全站仪对超高层建筑的动力特性进行识别，得到了结构的自振频率。Li 等［8］利用GPS/BDS 技术对超高层结构进行变形监测，并采用改进的模糊函数法提高监测精度。目前，GNSS 技术可用于超高层或高耸结构的动态变形监测［9-10］。

在利用实时动态差分技术的全球卫星导航卫星系统（GNSS-real-time kinematic，GNSS-RTK）监测时，因外部因素及仪器本身的影响，致使结果存在一定误差。RTK 系统内部差分技术可消除大部分误差，但无法消除多路径［11］和随机噪声等背景噪声。各种滤波算法是减弱背景噪声的实用方法，如小波分析［12］、经验模态分解（empirical mode decomposition，EMD）［13］。对于复杂的带噪信号，单一的小波无法达到最佳的降噪效果；EMD 会引起模态混叠现象。近年来，集合经验模态分解（ensemble empirical mode decomposition，EEMD）［14］和完备集合经验模态分解（complete ensemble empirical mode decomposition，CEEMD）［15］常用于信号降噪，但EEMD 会有较大的信号重组误差，CEEMD 会因为添加的辅助噪声而分解出额外的模态数。EEMD-切比雪夫联合滤波被初步用于海洋平台的信号降噪［16］，但EEMD 信号重组误差和结构模态参数识别等问题却仍未解决。添加自适应噪声的完备集合经验模态分解（complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN）及相应改进算法的重构误差相对较小［17］，其不足是有效信息成分出现较“晚”，在分解得到的本征模态函数（intrinsic mode function，IMF）中容易出现多余的分量。

变分模态分解（variational mode decomposition，VMD）［18］不仅能够避免模态混叠问题，还有良好的信号重组能力。该算法在轴承故障诊断中取得了一定成果［19-20］，但较少用于GNSS-RTK 的数据分析。据此，本文基于改进的VMD 来提取RTK 监测结果中的信息分量。

模态识别是进行结构动态监测的重要任务，其中频率和阻尼比更是起到关键作用。准确识别各模态参数成为了研究结构动力特性的热点。

接下来，本文利用GNSS-RTK 技术对高耸结构进行实时动态监测，并对背景噪声进行分析。通过提出改进的VMD 与小波阈值（wavelet threshold，WT）相联合的方法（ACVMD-WT）对数据进行降噪处理，并与EEMD，CEEMDAN 和CEEMDAN-WT 进行对比，验证所提方法的优越性。最后，通过模态分析得到结构的频率和阻尼信息，把握结构的动力特性。

1 GNSS-RTK 定位误差及噪声分析

本次监测的高耸结构处于大面积的水域环境中。为研究仪器定位误差和水域对监测结果的影响，先选择类似的水域环境进行测试，并选取泥砖地作为对比环境。

如图1 所示，将1 套RTK 作为基准站放置在远离遮挡的空地上，其余2 套作为移动站放在泥砖地和水域环境中。水域半径为50 m，两基准站与移动站的距离分别为60 和700m左右。仪器高度截止角为15°，风力为3～4 级，温度为8～10 ℃，数据采集时间为12 h。

图1 设备布置Fig.1 Equipment arrangement

仪器在水平方向（x，y）的定位精度（1 cm）优于在竖直方向的定位精度（2 cm），且在后续试验中结构的水平位移将作为分析重点，因此，图2 给出了RTK 测试结果的水平方向云点图。

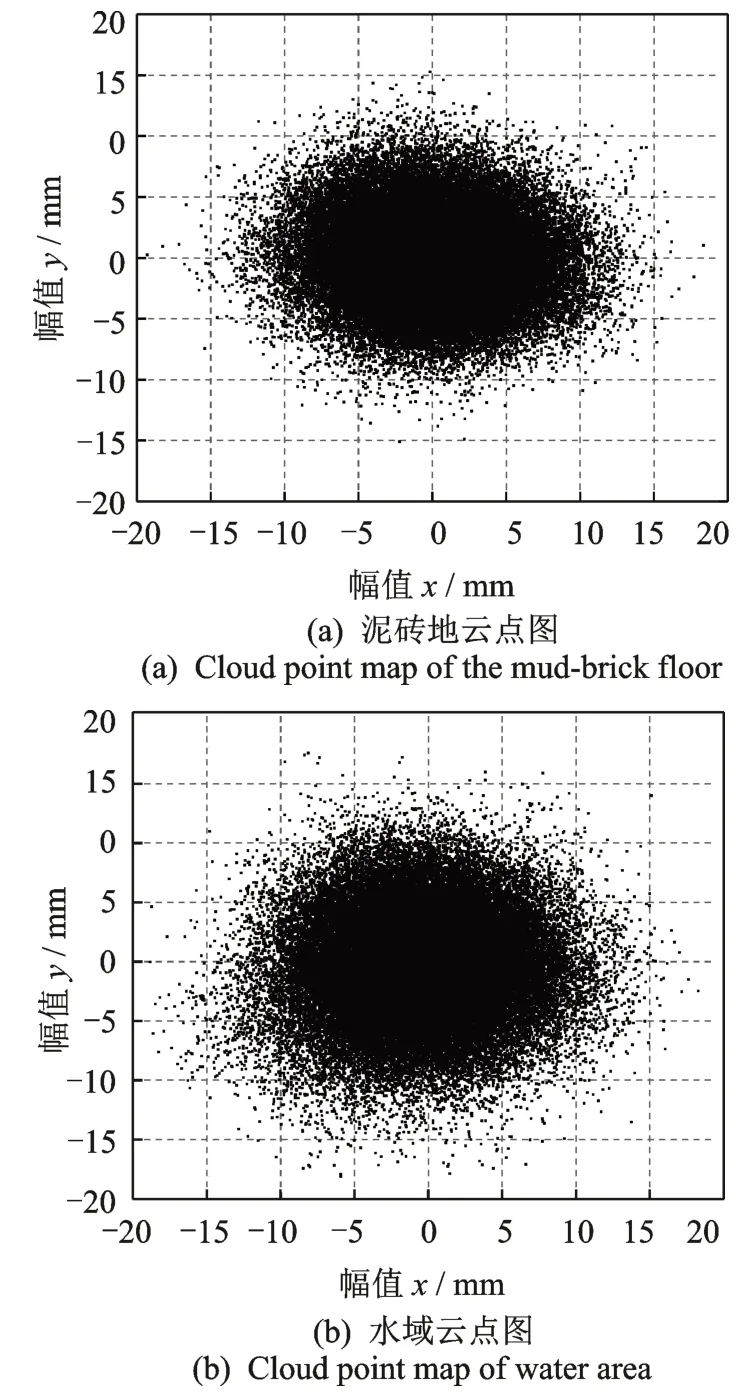
图2 水平方向云点图Fig.2 Cloud point maps of horizontal direction

由于两移动站所处位置均为固定点，理论上坐标点也应均为定值。但在图2 中，两场地坐标点呈“散乱”状态，故其幅值变化代表了RTK 产生的误差。由RTK 工作原理和误差来源可知，其误差主要来源于背景噪声。从图2 中可以看出，在x方向，两者的幅值基本在±15mm内；而在y方向，水域的幅值总体上大于泥砖地，甚至有些超过18 mm，水域云点图的离散度也大于泥砖地，表明水域环境引起的噪声误差稍大。主要原因是光滑水域更易对卫星发出的信号形成反射现象，致使GNSS-RTK 接收机接受更多的反射信号，从而引起相对更大的误差。此外，两云点图形状也存在差异，图2（a）呈椭圆状，而图2（b）更倾向圆形状，说明这两者信号的反射点位置与反射方向有所不同。

表1 给出了两场地环境水平方向幅值的均方根（root mean square，RMS）值，RMS 越大，表明误差越大。在表1 中，一方面，两环境周围信号反射媒介的影响导致y方向的RMS 值均小于x方向；另一方面，水域在x和y方向的RMS 值均大于泥砖地，且在x方向的RMS 值最大，再次证明了水域总体上产生的背景噪声更大。

表1 水平方向均方根值Tab.1 RMS values in the horizontal direction

以上分析有助于理解包括水域在内的环境产生的背景噪声对RTK 监测结果的影响。同时，需要合适的滤波算法对监测数据实施降噪处理。

2 改进的VMD-WT 降噪方法

2.1 VMD 原理及性能评估

VMD 算法的核心步骤如下［21］：

1.通过对各IMF 进行Hilbert 变换获得相应的各解析信号。

2.将各IMF 与相应的频率指数项相乘，并把各IMF 的中心频谱进行调整，将频谱转移到基带上。

3.基于高斯平滑估计，求出解调信号的各IMF宽带，然后通过变分约束函数对其进行求解，变分约束函数表达式为：

式中 ∂t为对t进行求导；δ(t)为单位脉冲函数；μk为k个有限IMF；ωk为各IMF 对应的中心频率；∗代表卷积为范数；j 为虚数单位；f(t)为原信号。

4.引入下式，将上述约束问题转化为无约束问题进行求解：

式中α为二次惩罚因子；λ为Lagrange 算子为向量间内积。

5.利用交替方向算子乘法将以上步骤进行迭代，各IMF 的带宽和中心频率也在迭代中进行更新。若得到式（1）中变分约束最优值，则算法终止。

为验证VMD 算法的适用性，选取仿真信号进行模拟试验：

式中x(t)表示纯净信号；X(t)由3 个正弦信号和随机噪声n(t)相加组成，如图3 所示。

图3 噪声信号Fig.3 The noise signal

对图3 信号同时实施CEENDAN 与VMD，在式（3）中，信号含有1.5，3 和5 Hz 三个频率，理论上VMD 分解只需设置3 个IMF。为对信号重组效果进行评估，VMD 分解设置的模态数与CEEMDAN自动分解得到的模态数相同（9 个IMF），故CEEMDAN 产生了多余的模态数。将以有效信息成分为主的IMFs 进行重组，如图4 所示，图4 显示经VMD 重组后的信号与原纯净信号匹配度更佳。利用均方根误差（root mean square error，RMSE）作为评价标准，RMSE 值越小，重组前后信号的拟合误差越低。CEEMDAN 和VMD 的RMSE 值分别为2.444 和1.877，表明VMD 相比CEEMDAN 能更好地适用于信号重组。

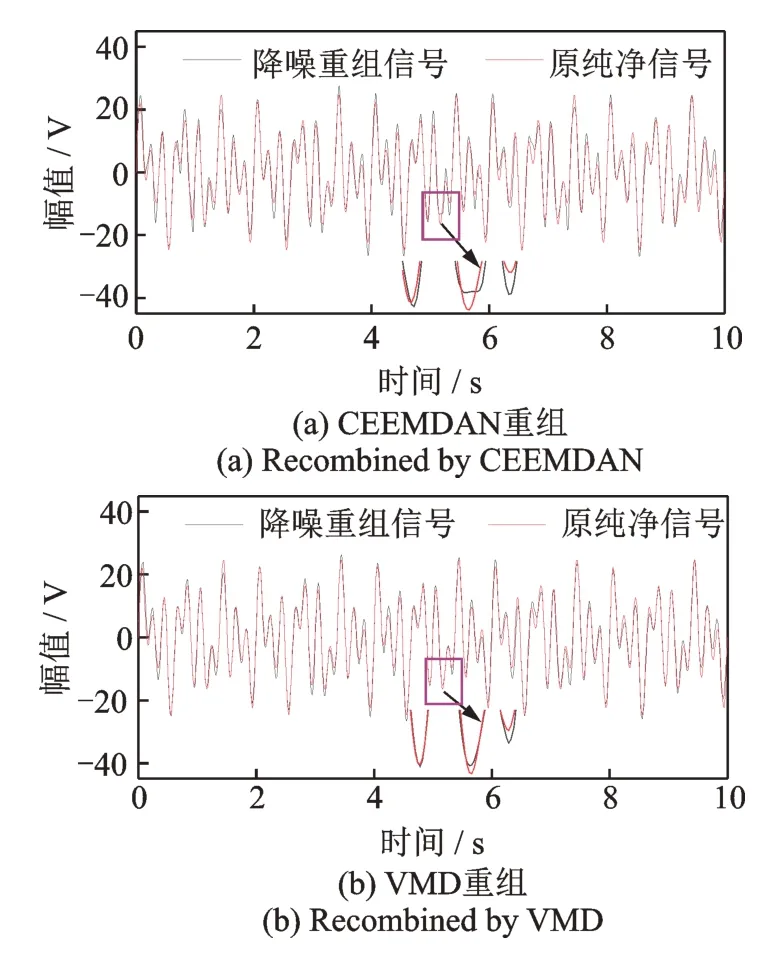
图4 不同方法重组信号Fig.4 Recombined signals by different methods

2.2 改进的VMD 算法

VMD 分解数的设置和模态分量的选取，是影响其分解和重组效果的两个重要因素。对于不同的分解数，信号重组误差均值不同，若重组误差均值最小，则分解数为最宜。同时，提出了自相关归一化函数（autocorrelation normalization function）和相关系数（correlation coefficient）综合对VMD 分解得到的IMFs 进行筛选，即ACVMD。

图5 为噪声信号与正常信号的自相关归一化函数。两种信号的峰值均出现在横坐标的零点处，在其余点处，噪声信号的波形基本稳定在零附近，而正常信号波形随时间上下波动。

图5 自相关归一化函数Fig.5 Autocorrelation normalization function

2.3 小波阈值（WT）

小波阈值可对噪声主导的IMFs 进行降噪，由于软阈值［23］得到的小波系数有良好的连续性，所得信号比较光滑，因此本文使用软阈值函数，其表达式为：

式中θj，k为小波系数；η为阈值；sgn(⋅)表示符号函数。

2.4 信号处理流程

如图6 所示，首先，对原始信号进行初步VMD分解，计算出不同分解数下信号的最小重组误差均值以确定最优的VMD 分解。然后，利用自相关函数和相关系数对分解得到的IMFs 进行筛选，保留有用的IMFs，同时利用小波软阈值对含噪为主的IMFs 进行降噪，以上过程即为ACVMD-WT 降噪。最后，将保留的IMFs 与降噪后的IMFs 进行重组，得到降噪后的信号，并利用模态辨识方法获取结构频率和阻尼信息。

图6 信号分析过程Fig.6 Signal analysis processes

3 结构动态监测与模态特性分析

3.1 ACVMD-WT 性能分析

在对高耸结构监测数据分析前，先利用GNSSRTK 实测信号分析不同噪声水平下所提方法的适用性。图7 分别为某桥梁和海洋平台的监测信号，监测频率分别为10 和1 Hz。在图7 中，两信号的噪声水平明显不同，后者信号噪声更为严重，无法准确识别其动态位移的变化情况。

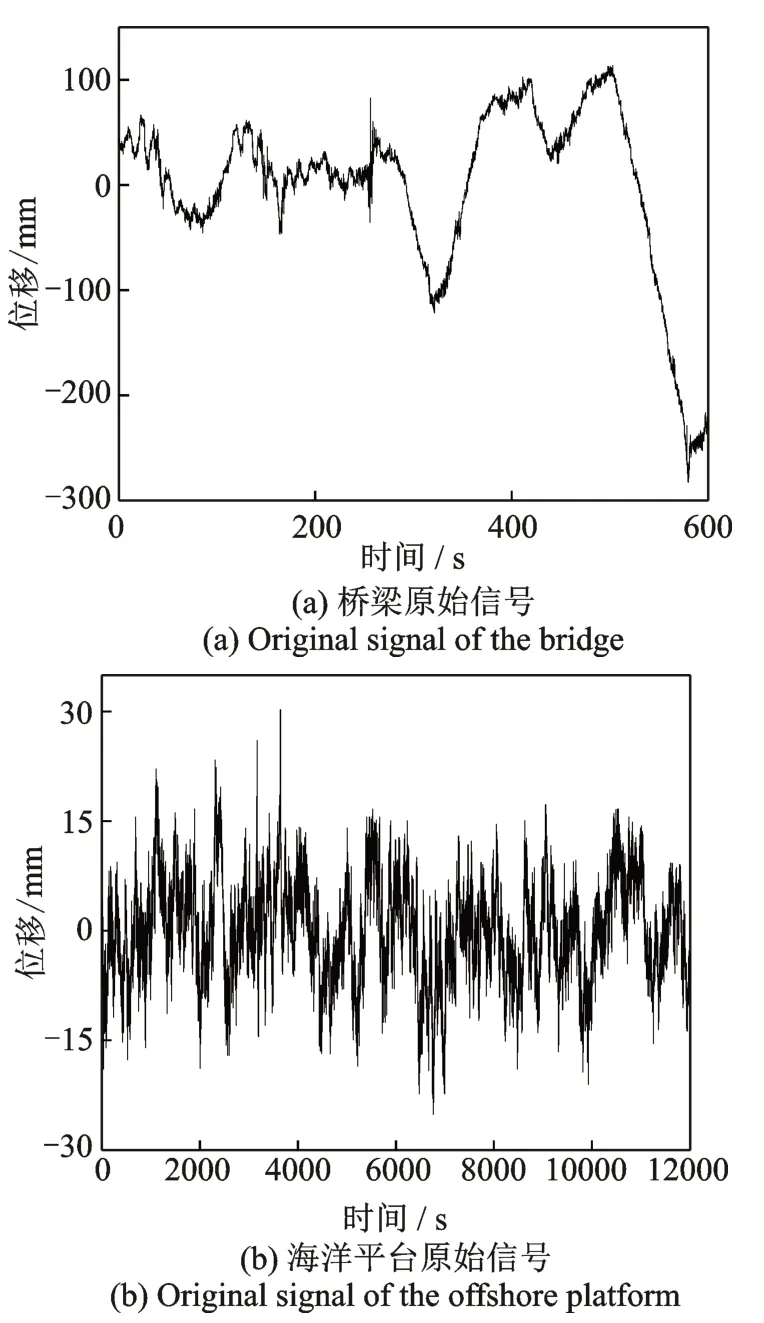
图7 不同噪声水平的原始信号Fig.7 Original signals with different noise levels

基于CEEMDAN 易出现多余分量的特性，设定两信号VMD 分解模态数低于CEEMDAN 分解得到的13 和15 个IMFs。VMD 不同分解数产生的信号重组误差均值如表2 所示。由表2 可知，分解数分别为5 和9 时，信号的重组误差均值最小。

表2 VMD 不同分解数的信号重组误差均值Tab.2 Mean value of signal recombination error for different decomposition numbers of VMD

图8 为两信号经VMD 得到的IMFs 及相应各IMF 的自相关归一化函数图。结合图8（a）～（b）可明显看出前两个IMF 为有用分量。基于图8（c）～（d），初步识别出第一个IMF 为有用分量，若直接舍弃其余各IMF，则有用信息会丢失，因此计算出图8（c）各IMF 与原信号的相关系数，前三个IMF相关系数值分别为0.749，0.482 和0.328，大于0.3，为非弱相关，予以保留。Daubechies（dbN）小波常用于工程信号的降噪，利用db6 小波软阈值分别对图8（a）的IMF3～IMF5，图8（c）的IMF4～IMF11进行5 层分解［24］。将降噪后的IMFs 与保留的IMFs 进行重组，如图9 所示。经降噪后，两信号的噪声水平显著降低。

图8 VMD 分解及相应的各IMF 自相关归一化函数Fig.8 VMD decomposition and corresponding IMF autocorrelation normalization functions

图9 降噪后信号Fig.9 Signals after noise reduction

为评价所提方法对不同噪声水平信号的降噪效果，另对两信号进行CEEMDAN-WT 降噪，并计算出信噪比（signal-noise ratio，SNR），RMSE 及相关系数。SNR 与相关系数值越大，表明降噪效果越佳，求解结果如表3 所示。从表3 中可以看出，本文方法的降噪指标均优于CEEMDAN-WT 法。且当信号噪声水平相对越小，改进的VMD 在有效减少IMF分解个数方面的优势越明显。

表3 降噪结果对比Tab.3 Comparison of noise reduction results

3.2 工程概况与设备布置

本次监测对象为天津广播电视塔（简称天塔），其全貌如图10 所示。天塔始建于1991 年，高度为415.2 m，自下而上分为塔基、塔座、塔身、塔楼、天线等。外筒为圆柱形筒体，直径从36.5m逐渐缩小至12.5 m，每10m的高度变坡一次，壁厚从1.8 m渐变至0.7m左右；内筒则是电梯及消防梯井，矩形截角筒体［25］。天塔不仅是电视调频广播发射中心，还承担娱乐、旅游等功能，更是世界上仅有的一座位于水中的高塔。鉴于天塔的多种重要功能，需定期对其进行健康监测。

图10 天津广播电视塔全貌Fig.10 The panorama of Tianjin Radio and Television Tower

试验时间为2021 年1 月13 日，地点在天津市河西区，空气湿度为18%，温度为9 ℃左右，风力为4～5 级，风速为1.2～6.6 m/s。主要的仪器为4套可同时接收GPS，GLONASS 及BDS 三种类型卫星信号的RTK。在天塔274m空旷位置处的东、西、南3 个方向（北方向遮挡严重，不再布置监测点）各放置1 套RTK 接收机作为移动站（D1，D2和D3），在水平距离移动站100m处的地面上放置1 套RTK 接收机作为基准站，如图11 所示。RTK采样率由1 Hz 提升到10 Hz，高度截止角为15°，试验持续进行10 h。

图11 现场仪器布置Fig.11 Field instrument layout

3.3 数据降噪处理

风荷载通常是影响结构水平位移变化的重要因素，3 个监测点水平方向（南北、东西方向）的位移变化如表4 所示。D3 监测点南北方向的位移波动变化大于东西方向的位移波动，而D1 和D2 则相反，且D1 监测点东西方向的位移最大值达到了97.1847 mm。

表4 监测点位移Tab.4 Displacements of monitor points

选取D3 测点的部分数据进行分析，如图12 所示。在图12 中，水平方向的位移在±40mm内变化，南北方向的位移（信号N）波动总体大于东西方向（信号W），与D3 点位移变化趋势相吻合。本次试验中的基准站与移动站距离仅为100 m，背景噪声是影响监测结果的重要误差来源。从图12 中可以看出，在噪声影响下，无法更好地识别天塔的动态位移，因此需要对原信号进行降噪处理。

图12 原始信号Fig.12 The original signal

依据2.4 节，利用VMD 对信号W 进行初步分解。为能有效设置VMD 分解的模态数，先对信号进行CEEMDAN 分解得到15 个IMF，因此VMD 分解的模态数不超过15 个。不同VMD 分解数得到的信号重组误差均值如表5 所示。由表5 可知，当模态数为12 时，信号重组误差均值最小，表明信号经VMD 分解为12 个IMF 最合理，如图13（a）所示。

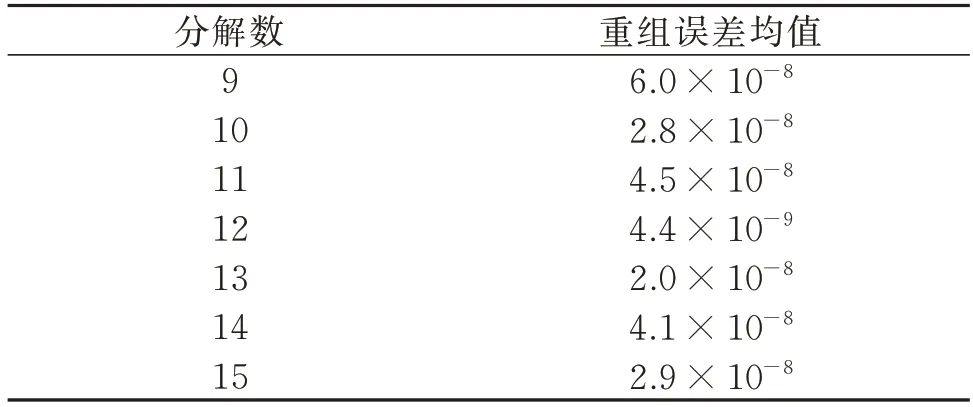
表5 不同VMD 分解数得到的信号重组误差均值Tab.5 The mean value of the signal recombination error obtained by different VMD decomposition numbers

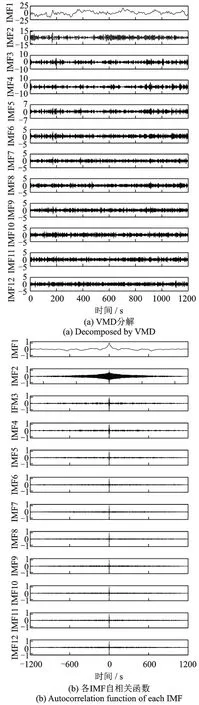
图13 信号分解及各IMF 自相关归一化函数Fig.13 Decomposition of the signal and autocorrelation normalization of each IMF

然后对各IMF 进行自相关归一化求解。由图13（b）可知，IMF1 和IMF2 含有更多的有用信息成分，为减少有用信息成分的丢失，利用相关系数对IMFs 进行进一步筛选，结果如表6 所示。

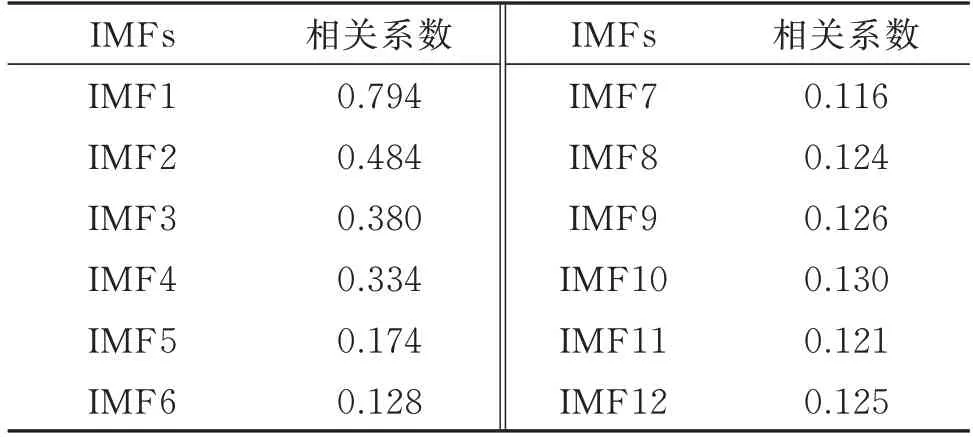
表6 各IMF 与原信号相关系数Tab.6 Correlation coefficient between each IMF and the original signal

由表6 可知，前4 个IMF 的系数值最大，与W 的相关性最好。后8 个IMF 的系数值均小于0.3，与原信号属于弱相关。基于各IMF 相关系数和自相关函数的综合分析，将IMF1～IMF4 作为有用IMFs。然后利用db6 小波软阈值对IMF5～IMF12 进行5 层分解降噪。最后将IMF1～IMF4 和处理后的IMFs进行重组，得到信号W1。同理，对信号N 进行相同步骤的降噪处理得到N1，如图14 所示。

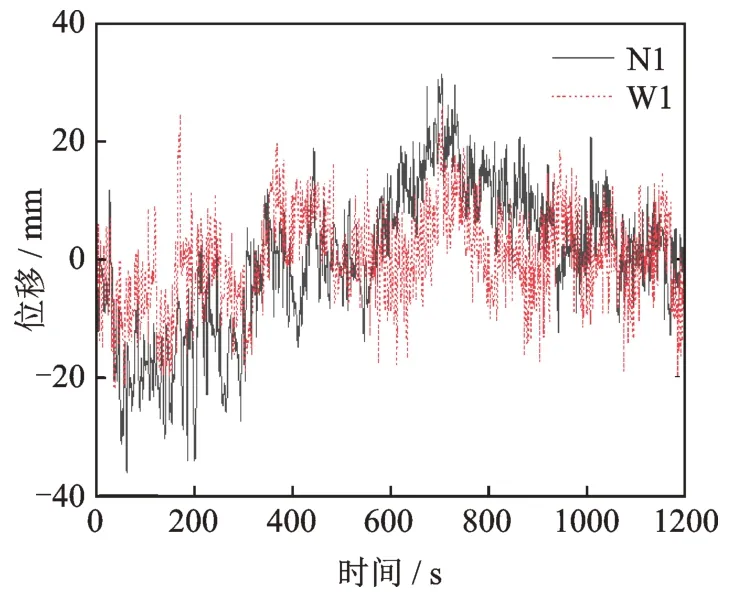
图14 重组信号Fig.14 The recombined signal

降噪后的位移基本在±30mm内，相比图12，尽管仍存有噪声，但其影响明显得到削弱。同时对信号N 和W 分别进行EEMD，CEEMDAN 和CEEMDAN-WT 降噪处理。表7 给出了不同方法降噪后的SNR，RMSE 及相关系数值。从表7 中可以看出，EEMD 的降噪效果最差，CEEMDAN 和CEEMDAN-WT 的降噪效果优于EEMD。而ACVMDWT 算法的SNR 分别为13.354 和10.120 dB；RMSE分别为2.617 和2.363 mm，优于前三种算法的评价指标，相关系数值也大于前三者。表明所提算法不仅能有效削弱噪声，还能保留信号有效信息。

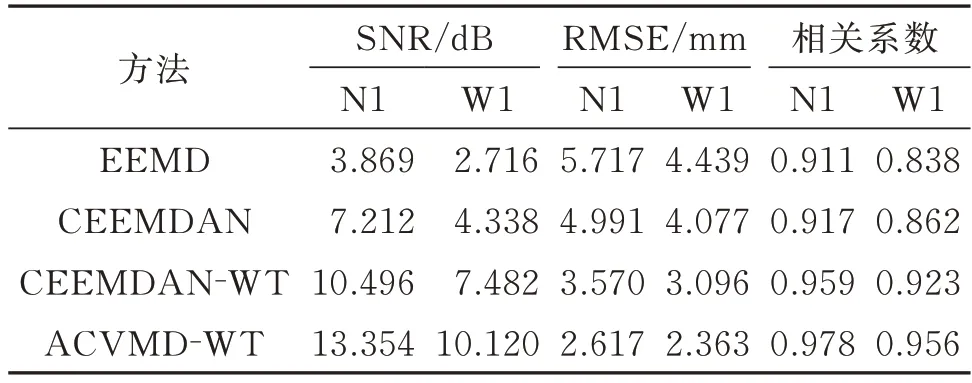
表7 不同方法降噪结果Tab.7 Noise reduction results of different methods

3.4 模态参数分析

对降噪前后的两信号进行快速傅里叶变换得到对应的功率谱，如图15 所示。由图15 可知，降噪后信号的频率峰值点更加明显，能更好地辨识出天塔水平方向的前三阶频率。第一阶频率均为0.1583 Hz，虽然第二、三阶频率带较为密集，但仍能从降噪后功率谱中准确识别出对应的频率，证明了ACVMD-WT 算法有助于提高结构频率参数的辨识度。

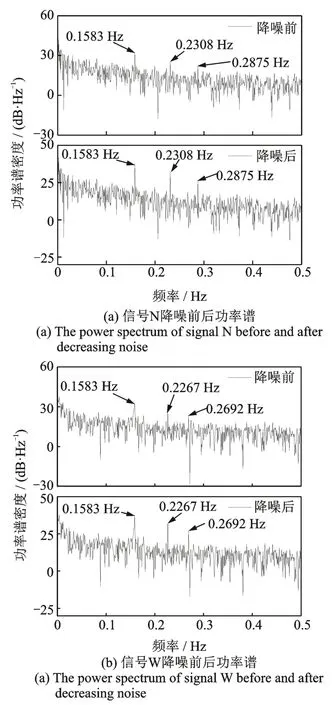
图15 降噪前后信号功率谱Fig.15 The power spectra of signals before and after noise reduction

本团队曾在2014 年对天塔进行过监测，并由有限元模型得到了结构前五阶频率（0.1586，0.2250，0.2763，0.3785 和0.4581 Hz）［26］。在此前试验中，RTK 采样率为1 Hz，仅得到了第一阶频率（0.1590 Hz），与有限元分析值的相对误差为0.252%。本次通过提升采样率和经更优算法的降噪处理后，识别出了更高阶数的频率参数。

如表8 所示，一阶频率与有限元相对误差为0.189%，小于此前误差，前三阶频率与有限元相对误差的最大值也仅为4.054%，说明在提高频率辨识阶数的基础上准确获取到了结构的前三阶频率；同时，也表明天塔在长期使用过程中其固有频率无显著改变，仍保持良好的结构特性。

表8 相对频率误差Tab.8 Errors of relative frequency

在表8 中，y方向（W1）的频率与有限元结果的相对误差相对更小，利用随机减量技术（random decrement technique，RDT）［27］获取到W1 含相应模态的自由衰减响应，如图16 所示。基于前人研究，本次子样本数为1000（通常大于400），截取时间为40 s。将自由衰减响应作为Ibrahim Time Domain（ITD）［28］的输入响应提取结构的阻尼信息，前三阶阻尼比分别为1.76%，3.36%和0.33%。