采用BP 神经网络优化的振动信号压缩感知方法
2023-11-20朱一凯陈安妮余哲帆万华平
朱一凯,陈安妮,余哲帆,万华平
(1.东南大学混凝土及预应力混凝土结构教育部重点实验室,江苏 南京 211189;2.浙江大学建筑工程学院,浙江 杭州 310058)
引言
结构健康监测已成为土木工程结构损伤演化行为研究的有效手段和服役安全保障的重要技术。结构健康监测是利用传感技术实时监测结构响应和环境变量,运用信号处理方法提取反映结构健康状态的特征量,进而对结构的服役状况进行评估[1]。新兴的无线传感网络技术具有成本低廉、安装维护方便、布点规模大、干扰性小等优点,逐渐被应用于大型土木结构的健康监测[2]。无线健康监测系统受传感器电池寿命、节点存储空间和传输带宽限制,难以进行长期、高频的数据采集工作。因此,寻求一种高效率的采样方法对于无线健康监测系统非常必要,有望解决无线传感网络的能耗问题,提升无线健康监测系统的工作寿命。
压缩感 知(Compressive Sensing,CS)[3]是一种新型采样理论,其利用信号的稀疏特性,通过少量的采样数据恢复出原始信号。CS 广泛运用于图像处理、雷达成像及核磁共振等领域[4-5]。在结构健康监测领域,CS 也逐渐得到研究人员的关注。Bao 等[6-7]使用CS 对山东滨州黄河大桥的健康监测数据进行分析,指出原始信号自身的稀疏性是成功实现CS的关键因素,而结构监测信号自身稀疏性往往有限。Yao 等[8]基于模拟退火算法和蚁群算法,探究了基于CS 的传感器布置方法,仿真和实测数据验证了该布置方法有效性。李惠等[9]将随机解调器植入传感器,用于产生随机采样矩阵,节省了传感器内存空间。Wan 等[10]基于时移策略构造特殊稀疏字典,适用于风速信号压缩与重构,并利用杭州东站屋面实测风速信号验证了该方法有效性。
对于实测信号,噪声污染不可避免,噪声污染会导致原始信号的稀疏性降低,而信号稀疏性又是影响CS 效果的重要因素。针对信号噪声问题,Deanna 等[11]提出了CoSaMP 算法,采用回溯策略来降低噪声干扰影响,但该方法效果对原始信号(无噪声污染)的稀疏性要求较高。Ji 等[12]和Huang 等[13]提出了多任务贝叶斯压缩感知方法,通过纳入噪声先验信息来降低噪声干扰,该方法依赖于信号相关性且计算较为复杂。康杰等[14]基于Polar 插值的改进正交匹配追踪恢复算法,能够重构稀疏性较低的信号,但该方法主要适用于频率泄漏引起的低稀疏性情况。
本文针对受噪声干扰且稀疏性较低的信号,提出利用反向传播(Back Propagation,BP)神经网络对LASSO 算法得到的稀疏系数进行优化,用于改善CS 效果。BP 神经网络将预期样本和输出样本的误差进行反向传播,通过反复迭代训练,得到优化的稀疏系数。本文提出了基于BP 神经网络优化的CS方法,可有效提升信号重构的精度,通过仿真数据和实测数据验证了该方法的有效性。
1 压缩感知基本理论
原始信号x∈RN经过观测矩阵Φ∈RM×N压缩观测,可以得到观测信号y∈RM,如下:
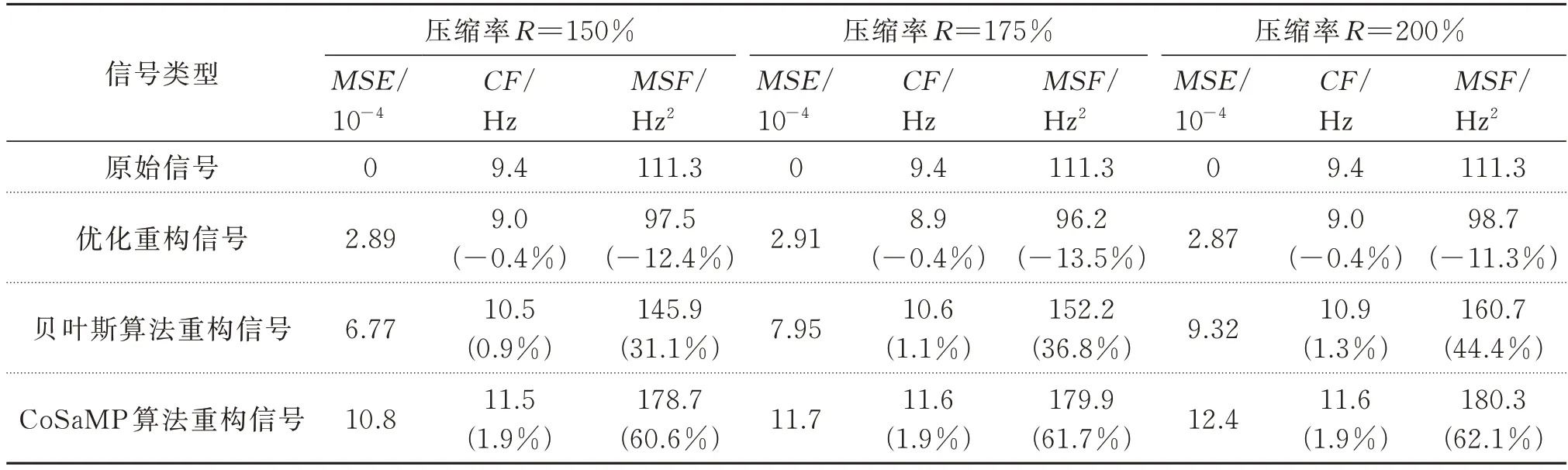
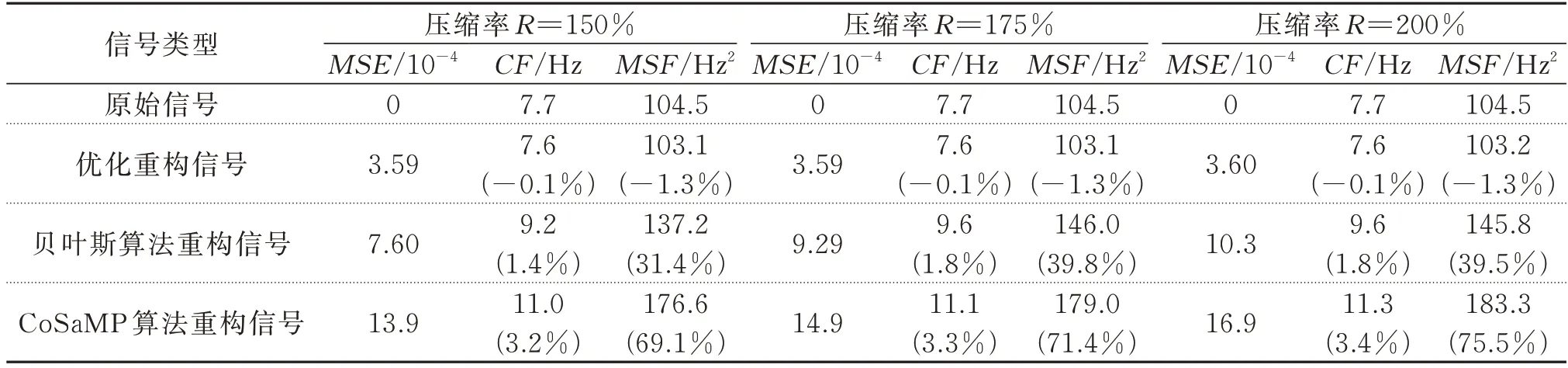
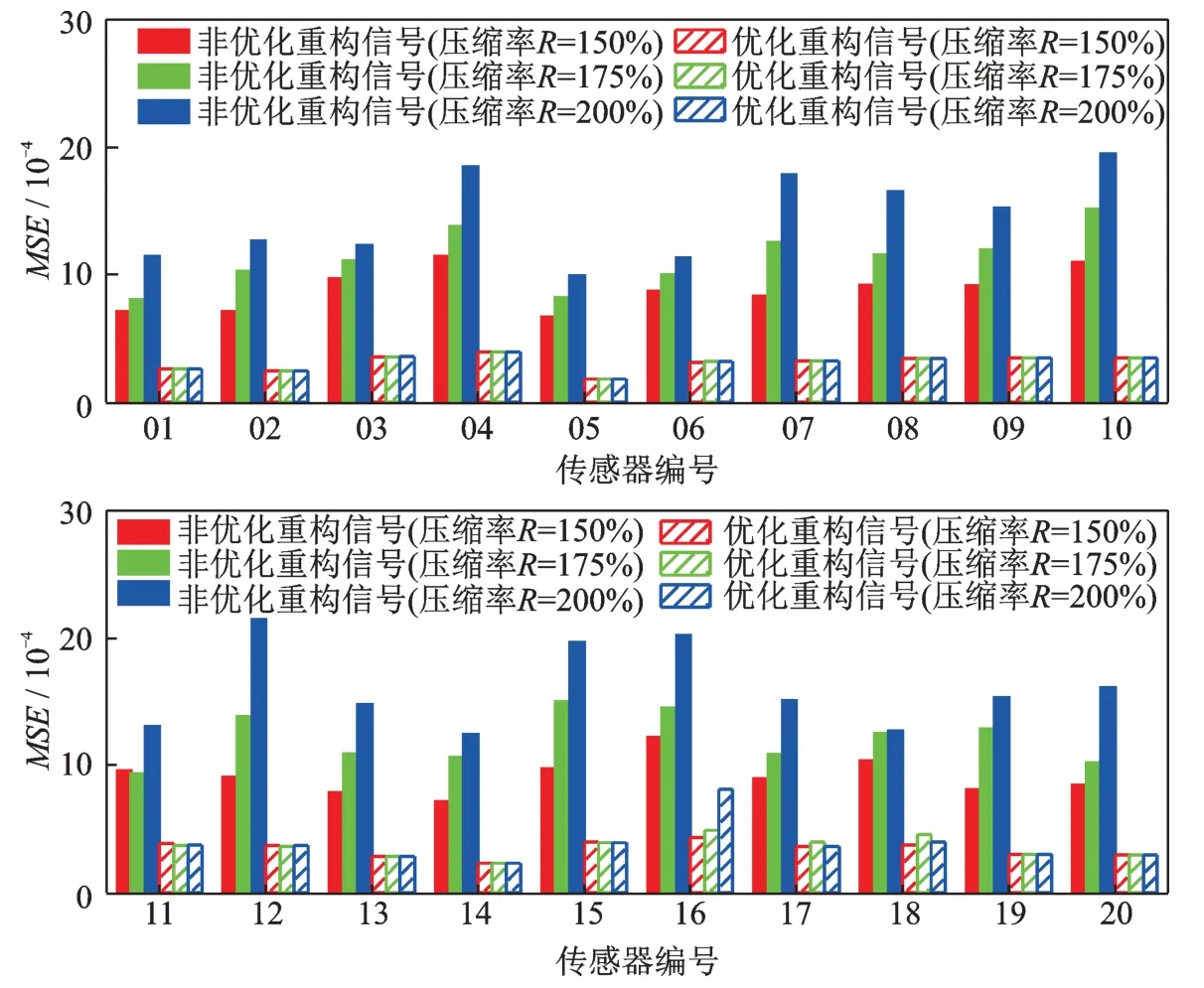
式中M和N的取值满足M 式中w为稀疏表示的系数向量。由式(2)可得: 将式(3)代入式(1),令传感矩阵A=ΦΨ,有: 根据方程(4),压缩感知问题可描述为:已知观测信号y和传感矩阵A,在w具有稀疏性的先验条件下,求解w。式(4)的求解可以转化为求解下式表示的l0范数问题: 式中‖·‖0为l0伪范数,表示向量中非零值的个数。 Candès 等[15]指出传感矩阵A满足有限等距性条件(Restricted Isometry Property,RIP)时: 式(4)可以解得唯一的稀疏解;当观测矩阵Φ为伯努利随机矩阵时,传感矩阵A通常可以满足RIP条件。且式(5)可以转变为求解下式的l1范数最小化问题: 式中‖·‖1为l1范数,表示向量各个分量的绝对值之和。 式(7)可使用LASSO 算法通过最小化方差来求解: 式中α为正则化参数,用来控制w的稀疏度,避免LASSO 算法出现过拟合的情况。 式(8)是连续的凸函数,可以通过迭代求解,解得稀疏系数w的估计值,通过式(3)计算得到信号的估计值。 若x为一加速度信号,在离散余弦基(DCT)上的表示具有“能量集中”的特性,稀疏性较好,通常DCT 选为变换基Ψ∈RN×N。 考虑到实测的加速度信号往往含有噪声,式(3)中引入了噪声项ε,得到: 将噪声 项ε在DCT上用系数向量wε表示,则式(9)转变为: 在信号传输过程中,传统方法传输完整原始信号x,未进行信号压缩。而CS 传输方法是将原始信号x乘以观测矩阵Φ得到压缩信号y,然后将压缩信号进行传输,实现数据压缩传输效果;在接收传输数据后,再求解系数向量(w+wε),并重构原始加速度信号x。但此时系数向量因受噪声干扰而稀疏性下降,利用LASSO 算法得到的解为粗略稀疏系数。为了降低噪声的干扰影响和提升压缩感知效果,在粗略稀疏系数和精确稀疏系数之间建立一个映射,采用BP 神经网络建立此映射。BP 神经网络具有极强的非线性映射能力,并适合处理大量复杂数据,具有得到接近精确稀疏系数的优化稀疏系数的潜力。 BP 神经网络如图1 所示,通常由输入层、隐含层、输出层3 个部分组成,每一层由若干神经元组成,层与层之间的神经元全数相连。神经元的输入是上一层神经元的输出,加权求和后加上阈值,代入激活函数,得到的输出传入下一层神经元。其对应的数学模型为: 图1 BP 神经网络及神经元结构Fig.1 BP neural network and neuron structure 式中pi为前一层中第i个神经元的输入;wi为对应的权值;n为前一层神经元的个数;b为该神经元的阈值;f(·)表示激活函数。 构建神经网络是一个循环迭代过程,不断调整和更新神经元的权值和阈值,直到输出值和目标值之间的误差满足要求,达到满意的拟合效果[16]。神经网络的输出值和目标值误差用均方误差定义,如下式所示: 式中ER(θ)为目标误差;wi为第i个权值参数;bi为第i个阈值参数;K为训练样本集中的样本个数;ξj为第j个目标量为第j个输出量;N为目标量的长度。 神经网络的优化问题转变成求ER(θ)最小值的问题,使用ADAM 优化算法[17]求解。ADAM 通过计算梯度的一阶矩和二阶矩估计,动态调整针对每个参数的学习率。其迭代式如下: 式中参数0≤β1<1,0 ≤β2<1,分别取0.9 和0.999。 本文方法结合了LASSO 算法和BP 神经网络,前者用于寻找初始稀疏系数,后者优化初始稀疏系数。LASSO 算法的目标是寻找稀疏系数中所有非零元素,但由于噪声干扰,能够较为准确地识别出稀疏系数中数值较大的非零元素。对于数值较小的非零元素,LASSO 算法求解精度较低,但数值较小的非零元素和数值较大的元素具有一定的相关性。LASSO 算法求解出初始稀疏系数和精确稀疏系数,其中较为精确的数值较大的非零元素与数值较小的元素具有一定的相关性。由于噪声的随机性较强,难以高效精确描述数值大元素与数值小元素间的相关性,为此根据初始稀疏系数来求解精确稀疏系数。而BP 神经网络具有极强的非线性映射能力,能够通过训练寻找初始稀疏系数和精确稀疏系数之间的非线性拟合关系,对初始稀疏系数优化,使其更加接近精确稀疏系数,达到优化重构精度的效果。 为了避免神经网络泛化能力受稀疏系数幅值大小影响,对稀疏系数进行线性归一化。对粗略稀疏系数及其对应稀疏系数归一化方法如下所示: 需对神经网络进行训练,预采集一段完整信号,分为K段长度为N的信号。根据式(2)和(15)计算得到归一化后的精确稀疏系数样本集为了消除稀疏系数幅值大小影响,对其进行线性归一化后再作为神经网络的目标输出;使用LASSO 算法得到粗略稀疏系数样本集,作为神经网络的输入,得到神经网络的实际输出为归一化的优化稀疏系数。利用ADAM 优化算法得到模型参数,建立BP神经网络。BP 神经网络训练完成后,采用新的压缩数据用来测试,对比粗略稀疏系数和优化稀疏系数的重构效果,以检验该方法有效性。优化稀疏系数的计算流程如图2 所示。 图2 稀疏系数优化的计算流程Fig.2 Calculation process of sparse coefficient optimization 用三层框架结构(如图3 所示)验证本文方法的有效性。每层楼板的质量表示为mi(i=1,2,3),每层楼的刚度系数为ki,阻尼系数为ci。每层楼板的质量、刚度系数、阻尼器系数分别为10 kg,1000 kg/m和10 N·s/m。则该三层框架结构的质量矩阵Μ、刚度矩阵K和阻尼矩阵C分别为: 图3 三层框架结构模型Fig.3 Structural model of three story frame 假设在每层楼板均装有加速度传感器,且传感器的采样频率设为50 Hz,采样持续时间为300 s。为了模拟结构振动响应,每层施加高斯噪声激励N(0,0.01);同时考虑测试噪声影响,计算得到的振动响应加入高斯噪声N(0,0.001)。仿真模拟采用的电脑计算平台是:Windows10 操作系统/Intel Core i7-9750H CPU/16G RAM,及数值软件是:Python 3.9+numpy 1.21.1+scipy 1.7.1。得到的楼板加速度信号如图4 所示。 图4 各层加速度信号采样值Fig.4 Sampling value of acceleration signal of each layer 定义采样率R=N/M,单次运算截取出长度N=200 的一维时间序列进行运算,对R=150%,175%,200%三种不同压缩率的情况进行讨论。在利用神经网络对粗略稀疏系数进行优化之前,需选取合适的LASSO 算法的正则化参数α,得到精度较好的稀疏系数,利于后续BP 神经网络对稀疏系数进行优化。 采用均方误差MSE=指标来评价重构信号的精度,其中K表示信号的段数。α依次取100,10-1,10-2,…,10-10,选用前1000 个数据来进行压缩感知和重构,计算结果如图5 所示。可知,当α=10-5时,LASSO 算法能够得到较高精度的粗略稀疏系数。 图5 不同压缩率情况下的均方误差与正则化参数的关系(框架结构模型)Fig.5 Relationship between MSE and regularization parameters under different compression rates(frame structure model) 前10199 个采样点通过步长为1、长度为200 的滑动窗构成10000 个N=200 的信号样本,生成10000 个精确稀疏系数样本和粗略稀疏系数样本。将得到的精确稀疏系数样本和粗略稀疏系数样本划分为10 组,每组有1000 个粗略稀疏系数样本及其对应的精确稀疏系数样本。前9 组数据用作训练集对神经网络进行训练,第10 组数据作为验证集,判断出合适的迭代次数。根据式(12)定义本文方法的目标误差ER=用于评价训练后的神经网络拟合精度。神经网络设置1 层隐藏层,输入、输出信号长度均为200,避免神经网络内部传递信息出现丢失或者冗余,将其神经元数量设置为200;初始学习率η设置为10-4。图6 展示了150%,175%,200%三种压缩率下在不同迭代次数下的目标误差ER。 图6 不同压缩率情况下的目标误差与迭代次数的关系(框架结构模型)Fig.6 Relationship between target error and iteration times under different compression rates(frame structure model) 由图6 可知,当迭代次数为4400 时,目标误差ER达到较小值,随着迭代次数继续增加,目标误差ER逐渐增大,因此迭代次数为4400 时的BP 神经网络的效果最佳。选择长度为5000 时的加速度信号作为测试集,将其分为25 段,每段N=200。对于测试集,利用上述方法得到粗略稀疏系数和优化稀疏系数,基于两种稀疏系数来重构信号,并计算各自的均方误差MSE,对比结果如图7所示。从图7中可以看出,本文方法得到的重构信号与原始信号的误差相对更小。 图7 重构信号优化前后的误差对比(框架结构模型)Fig.7 Error comparison before and after optimization of reconstructed signal(frame structure model) 为更加直观展示重构效果,将重构出的时域信号和频域信号及其误差展示在图8 和9 中。从图8和9 中可以看出,对于第1 层楼板的加速度信号,优化稀疏系数重构出的信号与原始信号之间的偏差在时域和频域都更小。 图8 重构加速度信号在时域内对比结果(第1 层传感器)Fig.8 Comparison results of reconstructed acceleration signal in time domain(layer 1 sensor) 图9 重构加速度信号在频域内对比结果(第1 层传感器)Fig.9 Comparison results of reconstructed acceleration signal in frequency domain(layer 1 sensor) 为了更全面展示本文重构方法的性能,将第1层优化重构信号与贝叶斯算法和CoSaMP 算法重构信号进行对比。采用误差指标MSE衡量重构误差,并引入频率重心指标CF=∑fi yi/∑yi和均方频率MSF=∑fi2yi/∑yi表征重构信号的频率特征,其 中,fi表示频 谱中第i个频率;yi表示第i个 频率对应的幅值。不同算法的指标对比结果如表1 所示。相较于其他重构算法,使用BP 神经网络优化的重构信号误差明显更小,并且重构信号的频率特征更加接近原始信号。 表1 不同算法重构信号的误差和频率特征对比(第1 层传感器)Tab.1 Comparison of error and frequency characteristics of reconstructed signals with different algorithms(layer 1 sensor) 为了更全面展示方法的可行性,对所有楼板的加速度数据进行分析。在三种不同压缩率的情况下,优化前后的加速度信号重构误差对比结果如图10 所示。使用BP 神经网络优化后,加速度信号的重构误差降低明显,表明本文方法用于仿真加速度信号重构精度高。 图10 不同测点优化前后重构信号的误差对比(第1~3 层传感器)Fig.10 Error comparison of reconstructed signals before and after optimization of different measuring points(sensors of layer 1~3) 用广州塔的实测加速度信号进一步验证本文方法的有效性。广州塔位于中国广东省广州市海珠区,总高度600 m,其中天线桅杆高146 m,塔身主体高454 m。广州塔的塔身主体布置了20 个加速度传感器(如图11 所示),采样频率为50 Hz。关于广州结构健康监测系统的更详细介绍,请参考文献[18]和网站:http://www.zn903.com/ceyxia/benchmark/index.htm。 图11 广州塔加速度传感器测点布置Fig.11 Measuring point layout of acceleration sensor of Canton tower 用广州塔底部编号01 传感器的加速度信号进行深入分析,同样考虑R=150%,175%,200%三种压缩率情况。根据上节提到的方法构建训练集、验证集和测试集。图12 展示了正则化参数α和均方误差MSE的关系,由12 图可知,当α取10-5时,粗略稀疏系数重构出的信号与原始信号误差最小。图13 展示了不同压缩率下和不同迭代次数与目标误差ER的关系。由图13 可知,当迭代次数取20000 时,目标误差ER达到较小值且不再明显减小,因此迭代次数为20000 时的BP 神经网络达到训练效果。 图12 不同压缩率情况下的均方误差与正则化参数的关系(广州塔)Fig.12 Relationship between MSE and regularization parameters under different compression rates(Canton tower) 图13 不同压缩率情况下的目标误差与迭代次数的关系(广州塔)Fig.13 Relationship between target error and iteration times under different compression rates(Canton tower) 同样地,选择长度为5000 的测试集,参照上一节的方法求得粗略稀疏系数和优化稀疏系数信号。基于两种稀疏系数重构出加速度信号,计算得到各自的均方误差MSE,结果如图14 所示。图14 表明,优化后得到的重构信号的误差更小。 图14 重构信号优化前后的误差对比(广州塔)Fig.14 Error comparison before and after optimization of reconstructed signal(Canton tower) 为更直观展示重构效果,重构加速度信号在时域和频域的对比结果如图15 和16 所示。由图15 和16 可得,优化后的重构加速度信号与原始加速度信号之间的偏差在时域和频域均更小。 图15 重构加速度信号在时域内对比结果(传感器编号01)Fig.15 Comparison results of reconstructed acceleration signal in time domain(sensor No.01) 图16 重构加速度信号在频域内对比结果(传感器编号01)Fig.16 Comparison result of reconstructed acceleration signal in frequency domain(sensor No.01) 为了更全面展示本文重构方法的性能,不同算法重构信号的指标对比结果如表2 所示。在三种不同压缩率的情况下,相较于其他重构算法,使用BP神经网络优化的重构信号误差明显更小,并且重构信号的频率特征更加接近原始信号。 表2 不同算法重构信号的误差和频率特征对比(传感器编号01)Tab.2 Comparison of error and frequency characteristics of reconstructed signals with different algorithms(sensor No.01) 为了更全面展示方法的可行性,用所有传感器的加速度数据进行分析,这里只展示重构信号误差的对比结果。在三种不同压缩率的情况下,优化前后的加速度信号重构误差对比结果如图17 所示。使用BP 神经网络优化后,加速度信号的重构误差降低明显,表明本文方法用于加速度信号重构精度高。 图17 不同测点优化前后重构信号的误差对比(传感器编号01~20)Fig.17 Error comparison of reconstructed signals before and after optimization of different measuring points(Sensor No.01~ 20) 噪声会导致振动信号的稀疏性下降,进而影响LASSO 算法用于信号重构的效果。本文提出了基于BP 神经网络优化的压缩感知方法,利用BP 神经网络对LASSO 算法得到的稀疏系数进行优化,提升振动信号的重构精度。用三层框架结构和广州塔验证本文方法的有效性,得到的结论如下:(1)LASSO 算法的正则化参数和BP 神经网络的迭代次数是本文方法的两个关键参数,选择合适的正则化参数可以获得较高精度的稀疏系数,选取合适的迭代次数可提升BP 神经网络的优化效果。(2)相比非优化的重构信号,基于BP 神经网络优化的重构信号与原始信号之间的偏差在时域和频域均更小,表明引入的BP 神经网络优化策略可有效提升压缩感知方法的性能。2 BP 神经网络优化方法
2.1 BP 神经网络原理

2.2 稀疏系数优化方法

3 仿真数据验证








4 实测数据验证






5 结论
