变厚度旋转圆柱壳的自由振动研究

2023-11-20李欣业桑建兵

振动工程学报 2023年5期

李涵，李欣业，白斌，钱毅，桑建兵，李想

（1.河北工业大学机械工程学院，天津 300401；2.湖南三一工业职业技术学院工程机械学院，湖南长沙 410129；3.核工业理化工程研究院粒子输运与富集技术国防科技重点实验室，天津 300180）

引言

旋转圆柱壳结构在工业领域中应用广泛，例如，高速旋转的离心分离器、航空发动机的转子系统等。在这些工程装备中，旋转圆柱壳结构所处的工作条件日趋严苛复杂，此外，为了进一步提高使用性能和工作效率，旋转圆柱壳结构的壁厚呈现出越来越薄的趋势，这些因素导致其结构振动问题日益凸显。此外，由于离心力和科氏力以及初始环向张力的影响，相对于静止的圆柱壳，旋转圆柱壳会出现特殊的行波振动现象。因此，对旋转圆柱壳结构振动特性的研究具有重要意义。

对旋转圆柱壳结构自由振动分析的求解方法有多种，例如，一些学者采用Galerkin 法对旋转圆柱壳的自由振动特性进行分析［1-5］，同时，微分求积法也常用于旋转圆柱壳的自由振动研究［6-11］。此外，与有限元方法相比，虽然Ritz 法难以分析几何形状复杂的结构，但其计算过程比较简单，且能保持较高的精度，因此仍被广泛应用于旋转圆柱壳的振动特性研究中。例如，李文达等［12］通过Ritz 法，采用改进的傅里叶级数位移形式，对弹性约束边界下的旋转薄壁圆柱壳结构的自由振动进行分析；还有研究利用Ritz 法，采用Gram-Schmidt 多项式构成近似函数，对旋转圆柱壳的自由振动进行分析［13-14］；Lei 等［15］运用无单元kp-Ritz 法，对旋转圆柱壳的自由振动进行了分析；Qin 等［16］通过Ritz 法，采用Chebyshev 多项式构成近似函数，研究了旋转圆柱壳的自由振动。但是，在上述研究采用Ritz 法对旋转圆柱壳振动特性进行求解的过程中，多采用傅里叶级数和Gram-Schmidt 多项式构成近似函数，较少采用Chebyshev 多项式，而Chebyshev 多项式在数值运算中具有正交性、快速收敛性和稳定性的优点［17］，比较适合构成近似函数。

此外，上述研究都未考虑旋转圆柱壳厚度变化的影响，然而在实际应用中，为了进一步减轻重量，旋转圆柱壳结构有时需要设计为变厚度的形式，即厚度沿轴向变化。因此，已有学者对变厚度旋转圆柱壳的行波振动特性进行了分析。Quoc 等［2］采用Galerkin 法对处在热环境下的变厚度旋转圆柱壳的振动特性进行了研究，但是该研究只考虑了一种厚度变化形式。

基于上述讨论，本文将考虑3 种厚度变化形式，并采用Chebyshev-Ritz 方法，比较不同厚度变化形式下旋转圆柱壳的自由振动，讨论转速、厚度变化参数和圆柱壳长径比等参数对变厚度旋转圆柱壳自由振动的影响，该研究将对旋转圆柱壳结构的轻量化设计具有一定意义。

1 理论建模

为了研究变厚度旋转圆柱壳结构的行波振动特性，首先对其进行理论建模。如图1 所示，圆柱壳结构以转速Ω绕其中心轴旋转，其长度为L，平均半径为R，（x，θ，z）为建立在圆柱壳中曲面上的正交坐标系，u，v，w分别为圆柱壳上任意一点沿x，θ，z三个方向上的位移分量。本文假定旋转圆柱壳的厚度h（x）沿其轴向线性变化，如图2 所示，可分为3 种变化形式，分别记为V1，V2 和V3。在这3 种不同的厚度变化形式下，圆柱壳上、下表面在坐标轴z方向上的坐标会发生变化，具体表达式如下：

图1 旋转圆柱壳结构示意图Fig.1 Schematic diagram of a rotating cylindrical shell

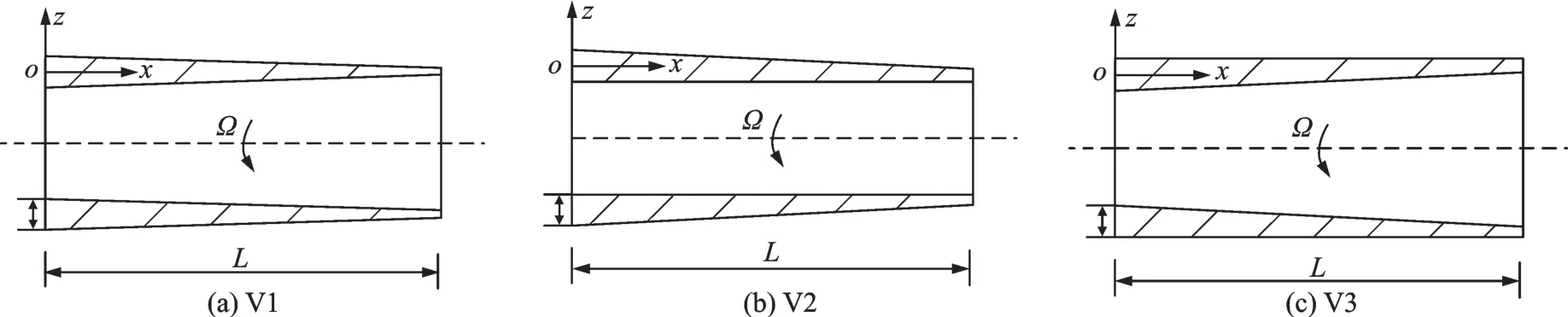
图2 变厚度旋转圆柱壳的3 种厚度变化形式Fig.2 Three varying forms of thickness for a rotating cylindrical shell with variable thickness

V1 厚度变化形式：

式中h1（x）和h2（x）分别表示圆柱壳上、下表面在坐标轴z方向上的坐标；h0表示圆柱壳初始厚度，即在x=0 时的厚度；kh表示厚度变化参数。

V2 厚度变化形式：

V3 厚度变化形式：

1.1 动能与势能求解

为了对所建模型进行固有频率的求解，本文采用Chebyshev-Ritz 法对变厚度旋转圆柱壳结构进行研究，因此首先需给出圆柱壳的动能方程与势能方程。

旋转圆柱壳上任意一点的速度向量可以表示为：

式中r表示旋转圆柱壳在坐标系（x，θ，z）上的任意一点的位移向量，可以表示为r=ui+vj+wk，其中，i，j，k 分别为沿x，θ，z方向的单位向量为r的一阶导数。

旋转圆柱壳的动能计算公式为：

式中ρ表示密度。

然后，将公式（4）代入公式（5），得到旋转圆柱壳的动能方程为：

根据Sanders 壳理论，旋转圆柱壳上任意一点的应变可以表示为：

旋转圆柱壳的应力应变关系表示为：

其中，E为材料弹性模量，μ为材料泊松比。

由旋转圆柱壳结构的变形引起的应变能可描述为：

由离心力引起的旋转圆柱壳的应变能表达式为［19］：

因此，变截面旋转圆柱壳的总势能方程可以表示为：

1.2 固有频率及模态振型求解

在上一小节得到的旋转圆柱壳动能方程与势能方程的基础上，本小节利用Chebyshev-Ritz 方法求解旋转圆柱壳固有频率及模态振型，并给出求解过程。

首先，旋转圆柱壳结构的位移场可表示为：

式中w1为旋转圆柱壳的固有频率；n为旋转圆柱壳行波模态的环向波数；U（x），V（x）和W（x）为模态函数，在本文中，这些模态函数通过Chebyshev 多项式和其对应的边界函数的乘积近似展开，具体公式为：

式中ai，bj和ck为未知系数；nmax表示在计算中被截断的项数；Pi(ξ)，Pj(ξ)和Pk(ξ)为第一类Chebyshev 表达式，可以用三角函数的形式表示为：

通过Chebyshev 多项式可以以较低的计算成本实现较快的收敛速度，并保持较高的精度，但是它定义在区间［-1，1］上，并在区间［-1，1］上才具有正交性，所以需要进行坐标变换，即ξ=2x/L-1。fu(ξ)，fv(ξ)和fw(ξ)表示沿ξ方向的边界函数，这些边界函数需要满足相应的旋转圆柱壳的几何边界条件，具体表达式如表1 所示。

表1 不同边界条件下的边界函数Tab.1 The boundary function for different boundary conditions

其次，由公式（6）和（12）可获得变厚度旋转圆柱壳的能量表达式为：

根据瑞利原理，最可能的近似值通过使关于未知系数的能量表达式Π最小而被确定，因此对能量表达式Π关于未知系数进行求导运算：

然后，公式（17）可以进一步转化为矩阵形式下的特征值问题：

式中P为由未知系数组成的特征向量，即旋转圆柱壳的振型，表达式为：

K为刚度矩阵，M1和M2为质量矩阵，具体表达式分别为：

其中，各矩阵的第i行、第j列元素分别为：

式中i0=d=h（x），Q66=G。求解方程（18），即可得到与固有频率相对应的振型。

2 数值结果与讨论

本节首先将计算结果与文献［18］和［20］中的结果进行对比，并对其收敛性进行研究，以验证本文建模方法的准确性与收敛性，然后通过参数研究分析变厚度旋转圆柱壳的自由振动行波特性。在本文中，除特别提及外，旋转圆柱壳的长度L=1 m，初始厚度h0=0.02 m，厚度变化参数kh=0.5，密度ρ=1072 kg/m3，弹性模量E=172 GPa，剪切模量G=4.2 GPa，泊松比μ=0.31，平均半径R=0.2，转速Ω=25 r/s，无量纲频率参数w*=wR，无量纲转速Ω*=ΩR，下标“b”和“f”分别表示后行波与前行波。

2.1 比较与收敛研究

为了验证本文建模方法的准确性与收敛性，本小节进行了两个算例研究。

2.1.1 算例1

如表2 所示，分别给出了两端固定（C-C）边界条件下厚度均匀的旋转圆柱壳的后行波和前行波无量纲频率参数，并与文献［20］中的结果进行了对比，而且还进行了收敛性研究，列出了不同截断项数下的计算结果。在本算例中，旋转圆柱壳的长径比L/R=10，厚径比h/R=0.05，泊松比μ=0.3，无量纲频率参数w*=wR，无量纲转速Ω*=，这里Ω*取0.0025。

2.1.2 算例2

如表3 所示，算例2 给出了两端简支（S-S）边界条件下厚度均匀的旋转圆柱壳的固有频率（Hz），并与文献［18］中的结果进行了对比。本算例中，圆柱壳长度L=0.256m，平均半径R=0.16 m，厚度h=0.0025m，弹性模量E=110 GPa，泊松比μ=0.31，密度ρ=4480 kg/m3，轴向半波数m=1，转速Ω=20000 r/min。

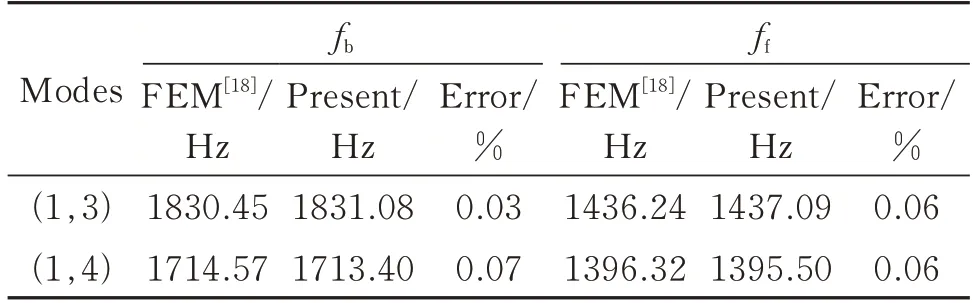
表3 旋转圆柱壳固有频率的比较Tab.3 Comparisons of natural frequencies for a rotating cylindrical shell

由表2 可知，本文得出的结果与文献［20］中的结果基本相符，研究表明计算结果随着截断项数nmax的增加而收敛到某一个值，当截断项数为11 时，计算结果已经收敛到一个足够准确的数值，因此在下列计算中截断项数nmax取11。

表3 的结果显示，本文所用建模方法得到的结果与文献［18］中的结果基本吻合，而且最大误差保持在1%以下。

总之，上述两个算例，验证了本文建模方法的正确性与收敛性。

2.2 参数研究

为了得到不同厚度变化形式下变厚度旋转圆柱壳的振动特性，本节在两端简支的边界条件下，讨论了不同的厚度变化形式、转速、厚度变化参数、圆柱壳长径比对变厚度旋转圆柱壳自由振动行波特性的影响，结果如图3～6 所示。

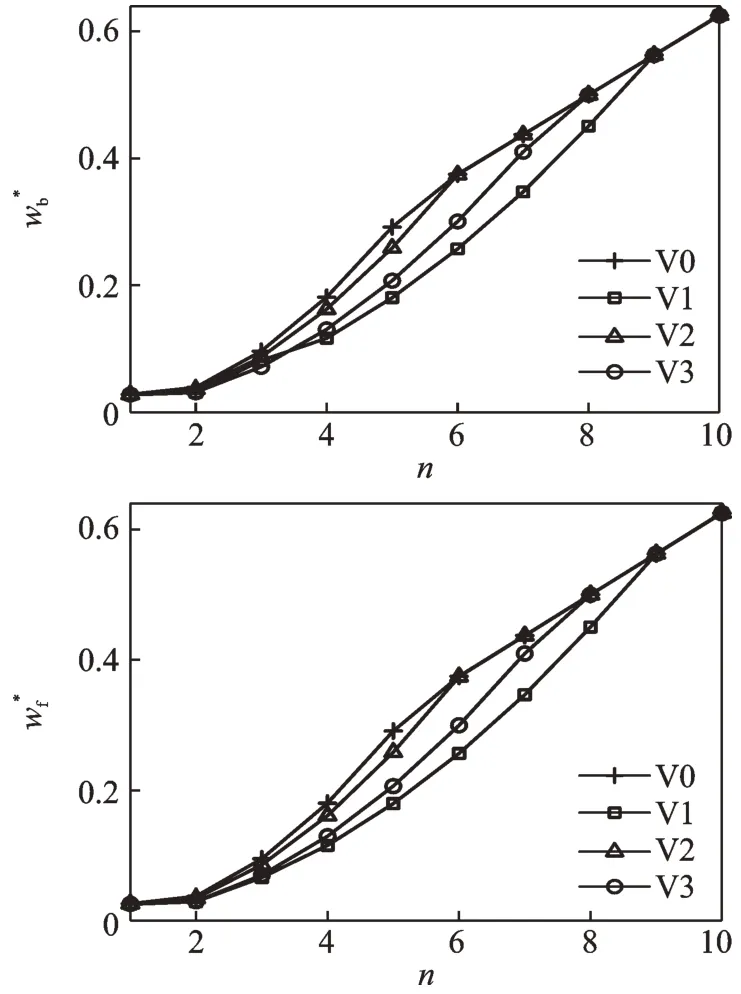
图3 变厚度旋转圆柱壳的无量纲频率参数随环向波数n 的变化情况Fig.3 Variation of the nondimensional frequency parameter for a rotating cylindrical shell with variable thickness with respect to the circumferential wave number n

图3 表示不同厚度变化形式下变厚度旋转圆柱壳的无量纲频率参数和随环向波数n的变化情况。图中V0 表示kh为0，即旋转圆柱壳的厚度是均匀的，在x轴方向上保持不变。

由图3 可知，所有厚度变化形式下的旋转圆柱壳的无量纲频率参数和都随环向波数n的增加而增加，并且V0 厚度变化形式下的旋转圆柱壳无量纲频率参数值最大，V1 厚度变化形式下的无量纲频率参数值最小。当不考虑特殊的V0 厚度变化形式时，V2 厚度变化形式下的旋转圆柱壳的无量纲频率参数值高于其他两种厚度形式下的无量纲频率参数，且比较接近V0 厚度变化形式下的无量纲频率参数值。从图3 中还可以明显看出，4 种厚度变化形式下的旋转圆柱壳的无量纲频率参数随着环向波数n的增加先由相同的初始值分散后又收敛于同一数值。

图4研究了当转速分别为0，25 和50 r/s 时，旋转圆柱壳在3 种厚度变化形式下的无量纲频率参数和随厚度变化参数kh的变化情况。由图4 可以看出，不同转速以及不同厚度变化形式下的变厚度旋转圆柱壳的无量纲频率参数都随着厚度变化参数kh的增大而逐渐减小，其中，V2 厚度变化形式下的无量纲频率参数的变化最小，且明显小于其他两种厚度变化形式下的无量纲频率参数的变化。此外，由图4 还可以发现，转速对无量纲频率参数随厚度变化参数kh增加而减小的变化趋势几乎无影响。

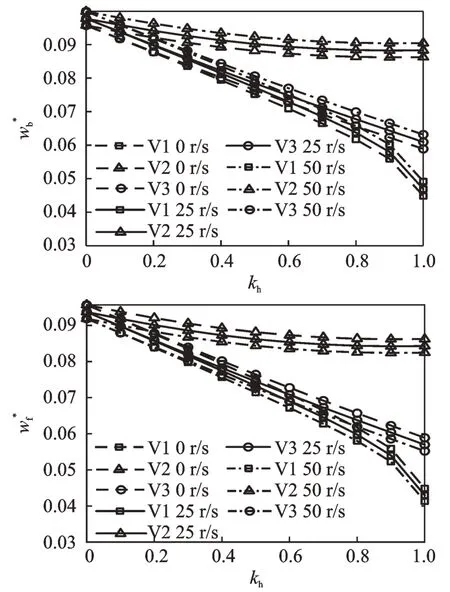
图4 变厚度旋转圆柱壳的无量纲频率参数随厚度变化参数kh的变化情况Fig.4 Variation of the nondimensional frequency parameter for a rotating cylindrical shell with variable thickness with respect to the thickness variation parameter kh

为了进一步研究转速对变厚度旋转圆柱壳自由振动的影响，图5 给出了变厚度旋转圆柱壳的无量纲频率参数w*随转速Ω的变化情况，图中BW 表示后行波，FW 表示前行波。由图5 可知，变厚度旋转圆柱壳的后行波无量纲频率参数随转速的增加而逐渐增大，而前行波无量纲频率参数随转速的增加而逐渐减小，其中V0 厚度变化形式下的前行波无量纲频率参数值和后行波无量纲频率参数值在不同转速下都是最大的，其次是V2 厚度变化形式。

图5 变厚度旋转圆柱壳的无量纲频率参数随转速Ω 的变化情况（kh=0.5）Fig.5 Variation of the nondimensional frequency parameter for a rotating cylindrical shell with variable thickness with respect to the rotational velocity Ω（kh=0.5）

最后，研究了几何参数对变厚度旋转圆柱壳的无量纲频率参数的影响。图6 给出了变厚度旋转圆柱壳的无量纲频率参数随长径比L/R的变化情况。

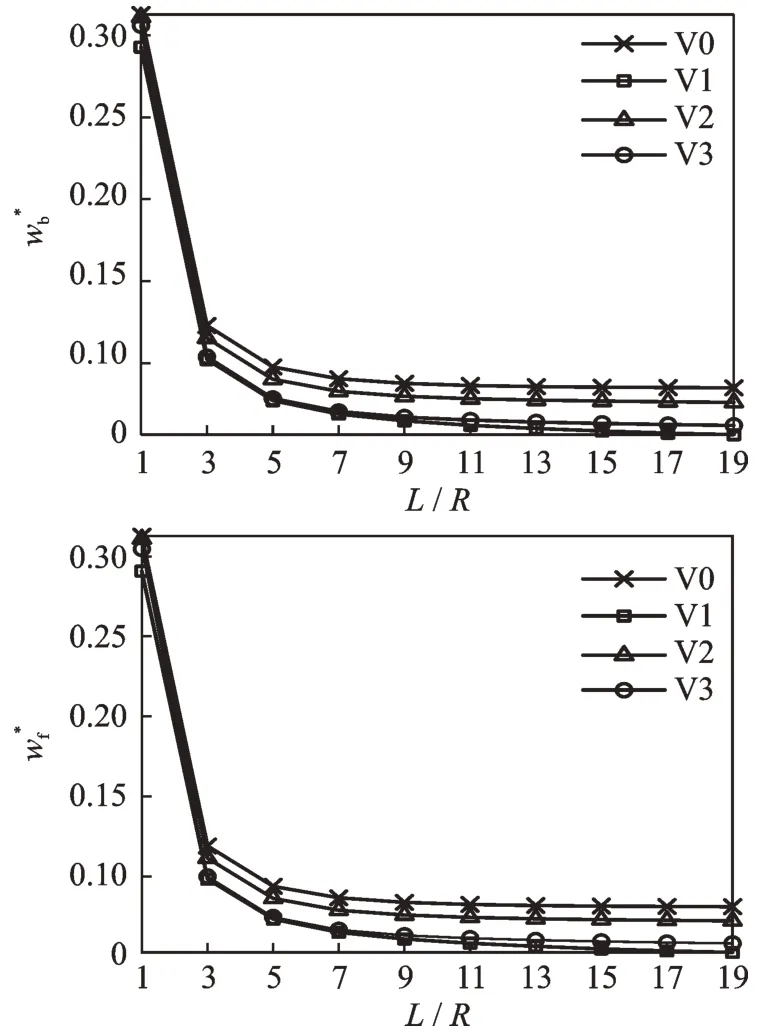
图6 变厚度旋转圆柱壳的无量纲频率参数随长径比L/R的变化情况Fig.6 Variation of the nondimensional frequency parameter for a rotating cylindrical shell with variable thickness with respect to length-to-radius ratio L/R

由图6 可以看出，变厚度旋转圆柱壳的无量纲频率参数随长径比L/R的增大而逐渐减小，具体而言，当长径比小于3 时，无量纲频率参数随长径比L/R的增大而迅速减小，当长径比大于3 时，无量纲频率参数随长径比L/R的增大而缓慢减小。而且，V0 厚度变化形式下的无量纲频率参数值在不同长径比下仍然是最大的，其次是V2 厚度变化形式，V1厚度变化形式下的无量纲频率参数值最小，且与V3厚度变化形式下相近。