基于颜色直方图和卡尔曼预测的目标跟踪算法

宋亚姬，戚晓艳，孙 艳

（空军航空大学 航空基础学院，吉林 长春）

引言

近年来无论在现代防御还是海上和空中交通管制系统中运动目标跟踪都是不可缺少的重要技术，随着现代航空航天事业及现代信息化战争的发展，运动目标跟踪技术得到了高度重视，成为计算机视觉领域的研究热点问题。所谓的目标跟踪是指在视频序列中检测目标，确定运动目标的位置、大小和目标运动轨迹，并实时估计其运动参数。由于目标跟踪在实现上非常复杂，在许多技术方面还不是很完善，因此对目标跟踪方法的研究具有重要的理论价值和广阔的发展前景[1]。

连续自适应均值漂移算法（Camshift）是通过统计迭代运算来寻找目标位置，算法简单容易实现，应用非常广泛。但是当目标较小或快速移动时容易丢失目标，有遮挡的情况下不能自我恢复跟踪。本文在此基础上进行了改进优化，用核直方图来计算目标的概率分布，应用Kalman 滤波来预测目标位置，并通过与Camshift 进行反复的跟踪迭代，在连续图像序列中实时搜索目标进行跟踪。通过仿真实验验证了算法的可行性。

1 基于颜色直方图和Kalman 预测的目标跟踪算法原理

1.1 直方图背投影

图像中物体颜色的全局分布即不同颜色在图像中出现的概率可用颜色直方图来描述，应用颜色直方图对运动目标进行跟踪，不容易受到目标快速移动、旋转等形状尺寸发生变化的影响。将原始图像通过颜色直方图转换为色彩概率分布图像的过程被称为直方图背投影。应用Camshift 算法进行目标跟踪首先要通过颜色直方图来提取目标图像的颜色特征[2]，实验中采集的图像通常为RGB 格式，由于Camshift 算法只能识别HSV 格式图像，因此要将图像转换为HSV格式。将目标的概率分布映射到观测图像，将颜色空间下的H 通道的灰度值反向投影，经过处理原图像转换成了灰度图像。

其中qu表示直方图中分量u 的像素值；c（xi）为像素xi的值；δ为Kronecker 函数。将直方图的尺度从[0,max(q)]变成[0，255]：

通过以上处理，将视频图像中目标的原像素点x的灰度值u 由其所对应的概率值pu代替，先求出图像的直方图，得到反向投影矩阵，即为直方图反向投影的过程。在此过程中将原来图像的灰度直方图经过计算出得出不同色度值的概率分布，就将原始图像通过直方图反向投影成了二维的色彩概率分布图。

1.2 Kalman 滤波原理

Kalman 滤波是一种高效率的递归滤波器，由状态方程和观测方程来进行描述，通过系统输入输出观测数据，对系统状态进行最优估计[3]。Kalman 滤波器由以下差分方程来描述系统的状态：

Kalman 滤波对控制系统的最优化估计包括两个关键环节：预测和修正。通过预测环节Kalman 滤波通过对当前系统状态建立观测模型到下一时刻系统状态的先验估计；在得到先验估计后，通过对先验估计和观测值的分析得到后验估计，此为修正环节。通过反复进行预测、修正，就实现了Kalman 滤波工作过程。

1.3 Camshift 算法

连续自适应均值漂移（Camshift）算法基于无参密度估计理论，在均值漂移算法的基础上扩展而来。CamShift 是一种自适应算法，能够对目标的大小和形状进行自适应调整，在目标尺寸和形状变化较大的情况下也能实现跟踪。在d 维欧式空间Rd中，核核密度估计为：

2 算法实现过程

为了提高在旋转、遮挡等复杂情况下的目标跟踪成功率，改善Camshift 算法图像分割耗时长、计算量大等问题，同时为了减少寻找目标的时间,克服颜色干扰的问题，在跟踪中引入了Kalman 滤波器。将Kalman滤波对当前帧图像中目标的质心位置的预测值与CamShift 算法跟踪结果进行比较分析来判定[4]。具体实现过程如下，其中i 为视频序列中图像的帧数：

（1） 计算直方图背投影，在初始帧图像中对搜索窗的位置和大小初始化，从搜索窗中的目标区域内提取目标的颜色直方图，同时提取目标的质心坐标，记为(xi，yi)，其中i=1，为初始帧图像。

（5） 更新模型，获取下一帧图像，跳转到第（2）步，重新执行搜索过程。

3 实验结果及分析

3.1 直方图背投影实验

为验证算法的可行性，用Matlab 软件进行了仿真实验。图1 给出了直方图背投影实验的部分实验结果。通过实验结果可知，如果把整幅图像设置为搜索区域，利用颜色直方图计算颜色概率分布时，与跟踪目标具有相似颜色特征的区域被一并保留，则跟踪结果受到一定程度的干扰。而设置合适的搜索窗后，在比搜索窗稍大一些的区域进行搜索时，可将搜索窗外区域的颜色概率视为零，从而大大减少算法的计算量，在较大程度上削弱与目标具有相似颜色特征的景物所带来的干扰问题。

图1 直方图背投影图

3.2 引入Kalman 预测的目标跟踪实验

当算法迭代超过15 次或相邻两次搜索得到的质心坐标差值在4 个像素以内时作为质心收敛的条件，将算法检测中提取的二值图像中目标的质心坐标与加入Kalman 滤波预测后实验结果进行比较。图2 给出了图像序列中第50、51、52 帧图像的跟踪实验结果。表1 给出了部分图像中运动目标质心位置经Kalman 滤波预测的结果，坐标以像素为单位。

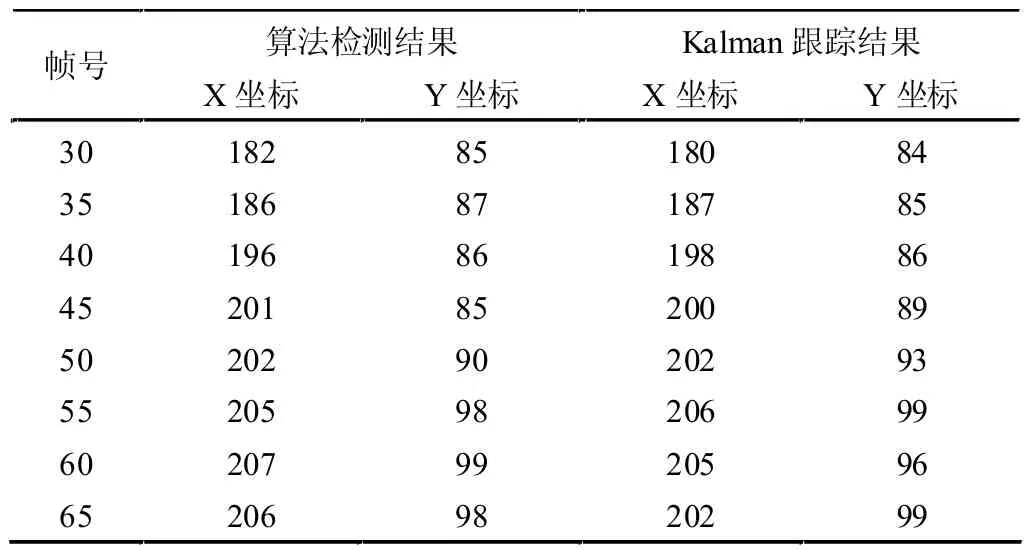
表1 Kalman 预测的目标质心部分实验结果

图2 跟踪实验结果

由图2 可知，引入了Kalman 滤波后减少了跟踪过程中对颜色的过分依赖，当目标遇到大面积颜色干扰时，可通过Kalman 滤波对目标质心位置的预测值来修正跟踪结果，实现准确跟踪。通过表1 数值可知，在同一帧图像中，在应用Kalman 预测之后跟踪结果的误差基本在4 个像素以内，误差符合预期目标，跟踪效果较为理想。

结束语

本文针对运动目标跟踪中常见问题进行了系统分析。应用颜色直方图建立目标的颜色概率分布，当目标存在旋转、变形等复杂情况下Camshift 算法跟踪目标容易丢失，为减少目标寻找与匹配的时间，提高跟踪效率，在算法中引入了Kalman 滤波器。在直方图背投影实验中，设置合适的搜索窗，搜索窗外的区域颜色概率视为零，在较大程度上削弱相似颜色特征带来的干扰问题。利用目标的外接矩形框大小、质心等特征对目标进行特征匹配，应用Kalman 滤波器对目标位置进行预测，为Camshift 算法提供起始点，将算法的最终收敛点作为每帧的跟踪结果，并将其返回给滤波器进行状态更新，反复迭代实现了对运动目标的连续跟踪。由于Kalman 滤波器具有计算量小，可实时处理等优点，引入Kalman 滤波后大大减少了算法的迭代次数，提高了算法的运算速度。仿真实验表明，该算法能够有效地抑制各自算法的不足，减少了算法的计算量，有效地提高了跟踪的成功率。