盲源分离通信抗干扰技术与实践

姚富强，于淼，郭鹏程,2，顾淼淼,3

（1.国防科技大学第六十三研究所，江苏 南京 210007；2.国防科技大学电子科学学院，湖南 长沙 410073；3.中国人民解放军31609 部队，江苏 南通 226141）

0 引言

由于信道的开放特性，无线通信容易受到无意和有意干扰，抗干扰能力是保密通信最基本的要求[1]。在战术通信领域，“通得上”和“抗得住”是2 个永恒主题，“抗得住”就是要保证在恶劣电磁环境和强电子对抗条件下的可靠传输[2]。通信抗干扰大概经历了扩谱抗干扰和智能抗干扰2 个发展阶段，目前正在向内生抗干扰方向发展[3]。

复杂电磁环境中，通信信号和干扰信号时频混叠，该场景与语音信号处理领域的“鸡尾酒会问题”相似。盲源分离致力于解决“鸡尾酒会问题”，旨在分离出共存的各语音信号，已成为当前信号处理和神经网络领域的研究热点。

盲源分离（BSS,blind source separation）是指在未知或少量先验信息情况下，仅利用观测混合信号对源信号和混合情况进行估计的理论与技术[4-5]。盲源分离起源于20 世纪80 年代，Hérault 和Jutten[6]提出了著名的H-J 算法，开创性地进行了信号盲分离研究工作。此后，学术界针对源信号独立性等理论和实践问题开展了大量研究[4-32]，形成了独立分量分析或独立成分分析（ICA,independent component analysis）等理论[4-8]，目前ICA 已经成为BSS 的主要解决方法。盲源分离已在生物医学[33-35]、语音[30-32,36-38]、图像[39]、视频[40]和水声[41-42]等信号处理领域得到广泛关注。由于无线信号分离和语音信号分离的相似性以及“盲”的优点，盲源分离技术被迅速用于无线通信侦察领域[43-45]，同时促进了盲源分离抗干扰技术的发展[46-57]。

根据接收通道数目m，盲源分离可以分为多通道（m〉1）和单通道（m=1）盲源分离。再根据源信号数目n与m的关系，多通道盲源分离又可分为超定（m〉n）、适定（m=n）和欠定（2≤m〈n）几种情况。单通道盲源分离原属于欠定盲源分离，但是，由于接收端仅有一个接收通道，基于矩阵的多通道盲源分离理论框架不再适用。鉴于单通道设备的普遍性，该技术在实际应用中具有非常重要的意义。因此，本文将单通道盲源分离抗干扰技术单独列出。

扩谱抗干扰以频谱资源为代价，其抗干扰能力与频谱资源之间存在固有矛盾，尤其在抗宽频段压制干扰时，这种矛盾更加突出。智能抗干扰技术需要认知电磁环境及协调抗干扰策略，大幅增加了勤务信令所需的时频资源开销，面临信令开销与系统效率之间的突出矛盾。实际应用中，以上两类矛盾往往难以调和，严重制约系统性能的提高。盲源分离在扩谱抗干扰基础上增加统计域维度，将时频混叠的通信信号与干扰信号分离开来，可在不增加频谱资源和勤务信令条件下提高通信抗干扰能力。盲源分离为解决以上两类矛盾提供了有效技术途径，推动通信抗干扰由“硬抗”向“容扰”发展。

1 盲源分离通信抗干扰基本原理

结合无线通信系统，盲源分离通信抗干扰技术原理如图1 所示。

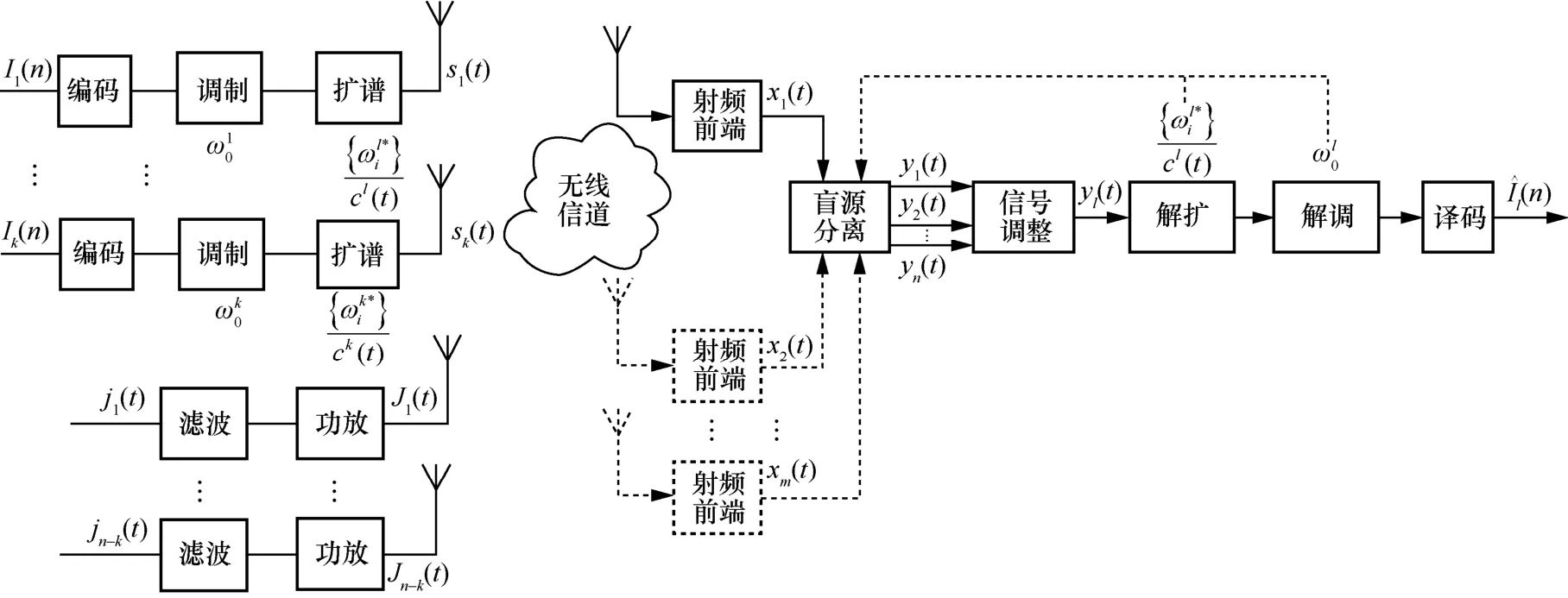
图1 盲源分离通信抗干扰技术原理

图1 中，源信号包括k个通信信号和n-k个干扰信号，即

源信号u(t)经无线信道传播后，接收端获得接收信号x(t)可写为

其中，m为天线数目。式(2)所示的接收信号为通信信号和干扰信号的混合形式。由于接收含有干扰信号成分，通信性能将受到影响。图2 以理想的线性瞬时混合为例，对图1中的信号混合和分离情况进行说明。

图2 盲源分离主要流程

图2 中，A为接收信号混合矩阵，W为分离矩阵，y(t)为分离信号，h[y(t)]为反映分离程度的目标函数，接收信号x(t)可表示为

其中，A={aij}，aij为混合系数，反映了第j个源信号到第i根天线传播信道的衰减情况；n(t)=[n1(t),n2(t),…,nm(t)]T为噪声信号。为便于观察，将式(3)写成向量形式，可以得到

式(4)表明，每路接收信号xi（t)(1≤i≤m）均为n个源信号的线性组合，同时含有干扰和其他信号成分。

如图2 所示，对于式(3)和式(4)所示的混合信号，盲源分离通过极大化h[y(t)]引导分离矩阵W迭代，使W逼近混合矩阵的逆矩阵（W≈A-1），从而实现信号分离，如式(5)所示。

将式(5)写成向量形式，可以得到

式(6)中，每一路分离信号yi（t)(1≤i≤n）对应一个源信号，与式(4)对比发现，信号得到有效分离。

实际应用中，式(6)所示的分离信号和源信号的次序对应关系具有不确定性，还需进行相关处理。图1 中的信号调整模块从分离信号中识别出有用信号并调整其幅度。设第l个信号为目标信号，后续模块对yl(t)解扩、解调、译码以恢复用户信息(t)。当接收端具有多个接收通道时，可通过多通道盲源分离技术进行分离；当接收端仅有一个接收通道时，可采用单通道盲源分离技术。接收端还可利用载频、跳频图案、直扩码等先验信息进行半盲源分离，以进一步提高分离性能。盲源分离主要受信号统计特性影响，与具体的通信技术体制不形成直接关系，对于未采用扩谱通信技术的场景，去除图1中的扩谱和解扩模块依然适用。

2 盲源分离通信抗干扰主要关键技术

结合无线通信实际情况，根据使用需求，重点讨论多通道和单通道盲源分离抗干扰等关键技术。

2.1 多通道盲源分离抗干扰技术

多通道盲源分离技术发展相对完善，但考虑背景噪声、信道衰落及天线数目等因素，需要关注降噪处理、卷积混合信号盲源分离及欠定盲源分离等问题。

2.1.1 小波降噪处理

独立分量分析通常先对混合信号进行白化处理，使之互不相关，再以独立性为目标函数，引导信号分离[5-6]。当混合矩阵各行线性相关性增大时，白化处理会放大噪声，对后续信号分离产生不利影响。因而，在信号分离前，需要对接收信号进行降噪处理。小波变换作为有效的降噪手段，可为盲源分离抗干扰提供帮助。

信号x(t)的连续小波变换的数学表达式为[58]

其中，T[x(t)]为小波变换系数，a为缩放因子，b为平移因子，φ(·) 为小波基函数。小波变换可以反映信号不同频率成分的细节特征，正信噪比情况下，信号的小波系数较大，而噪声的小波系数较小。

根据阈值选取规则确定门限值，保留（硬阈值方法）或者收缩（软阈值方法）超过门限值的小波系数，最后利用处理后的小波系数重构信号即可消除或减小噪声[58]。

但是，小波降噪性能受小波基、阈值选取规则、分解层数、阈值处理方法等参数影响，参数空间巨大。文献[59]结合理论分析和仿真实验，明确了适合跳频信号盲源分离抗干扰的降噪参数集，当干信比等于10 dB 时，小波降噪盲源分离较未降噪盲源分离容忍噪声强度提高了约2.5 dB。

2.1.2 卷积混合信号盲源分离

当无线信道存在多径衰落时，接收信号为源信号的卷积混合形式。参考线性瞬时混合模型图[60]，卷积混合信号盲源分离过程如图3 所示。

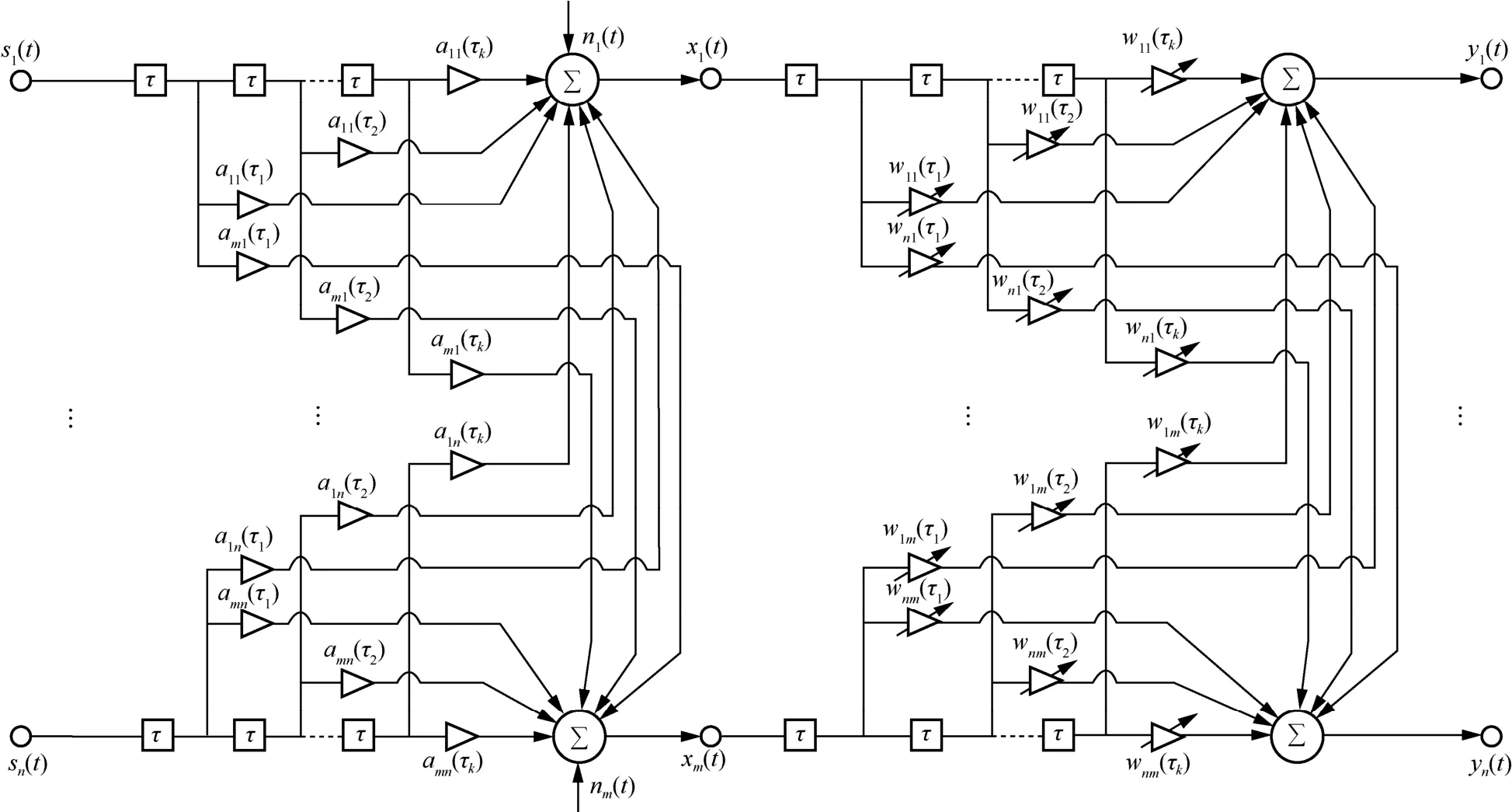
图3 卷积混合信号盲源分离过程

图3 表明，在混合过程中，信号不但存在幅度衰减，还出现多条传播路径，接收信号可表示为[4]

其中，每个源信号sj(t)均有K条路径，每径的幅度衰减为aij(τk)，时延为τk，噪声为ni(t)。如图3 所示，对于式(8)所示的混合信号，直观的方法是通过有限冲激响应（FIR,finite impulse response）滤波器的方式进行信号分离，如式(9)所示[4]

由于时域卷积对应频域相乘，可将卷积混合信号转换至频域进行分离[4,15-17]。对式(8)进行短时傅里叶变换，可以得到[16]

其中，v为短时傅里叶变换的帧号。转换至频域后，信号的混合模型重新变成线性瞬时混合形式，已有的复数盲源分离算法均可以实现频域分离。

由于盲源分离固有的次序和幅度模糊问题会给信号拼接带来困难，频域分离信号需要进行次序和幅度修正，最后通过傅里叶逆变换恢复时域信号。由于每段数据的长度与多径数目存在一定关系，分段长度在实际中要合理选取[16-17]。分离矩阵含有的波束信息以及相临分段间信号的相关性，均可用于对分离信号的次序和幅度进行修正[17]。

自20 世纪90 年代被提出以来，特征矩阵联合近似对角化（JADE）算法以其出色的分离精度和处理速度[49]，已经成为经典的盲源分离算法之一，一些研究工作直接采用JADE 算法[61]或将其作为对比算法[62]。因此，本文利用JADE 算法进行时域分离，同频域分离方法进行性能比较。一组卷积混合信号的分离结果如图4 所示。

图4(a)展示了噪声阻塞干扰信号和通信信号（2FSK 调制）波形；混合信号波形如图 4(b)所示，仿真中设定每路信号含有3 条路径。图 4(c)为采用JADE 算法的时域分离信号波形，图 4(d)为频域分离信号波形。从图 4(c)和图 4(d)可以定性看出，频域盲源分离方法对卷积混合信号的分离性能优于时域分离方法。

相关系数是衡量信号相似程度的重要指标，信号X和信号Y的相关系数定义式为[63]

其中，相关系数ρXY取值为0～1，当ρXY=0时，2 个信号不相关；当ρXY=1时，2 个信号相关性最强。盲源分离抗干扰技术追求的主要目标是从含干扰的混合信号中分离出的通信信号与原通信信号完全相关，即相关系数为1。图4 所示的结果中，JADE算法的时域分离通信信号与原通信信号的相关系数为0.813 1，频域盲源分离信号对应的相关系数为0.962 7，性能提升约18.40%。

2.1.3 欠定盲源分离

传统超定和适定盲源分离可以通过矩阵求逆的方法估计混合矩阵，进而实现信号分离[7]。但是，无线通信经常遇到接收天线数目少于源信号数目的欠定情况。此时，盲源分离需要通过较少混合信号分离出较多源信号，由于混合矩阵为病态，求解过程较超定和适定情况更加复杂。针对欠定盲源分离的特殊性，通常采取“两步走”的方法：先估计分离矩阵，再恢复源信号[18]。

学术界将基于稀疏性的信号处理的方法称为稀疏分量分析（SCA,sparse component analysis）[19]。SCA 已经成为欠定盲源分离的重要解决途径[19-22]。稀疏是指矩阵或向量中多数元素取值为零，仅有极少数元素取值为非零[20]。一般来说，时域信号非稀疏，经过短时傅里叶变换或小波包变换后，变换域信号通常具有较好的稀疏性[20-21]。利用信号稀疏性进行欠定盲源分离的原理比较直观，即使源信号数目较多，但只要每个时刻“活跃”（取值为非零）的源信号数目少于或等于接收天线数目，即可实现信号分离。

为便于分析，假设源信号足够稀疏，多数时刻仅有一个非零元素。对于非零元素多于一个的情况，该方法仍然成立。对于第一个源信号取值为非零的L个源信号列向量u(i1),u(i2),…,u(iL)，u(i1)=[s(i1),…,J(i1)]T，有[20]

在1～n中选取一个数值q，利用式(12)可以构建如下矩阵[21]

式(13)右侧每一列均对应着混合矩阵A的第一列a1，经过平均以后即可得到a1的近似估计。因此，在K个时刻按照式(13)构建矩阵，由于存在n个源信号，K列将主要有n种取值，对应着混合矩阵的n个列向量。已知数据的分类数目n，较多算法可以将信号聚类并估计其中心位置d（i1≤i≤n）。由式(13)可知，每个聚类的中心对应着混合矩阵的一个列向量[18]，从而可以实现混合矩阵估计[20-21]。当源信号稀疏性稍弱时，聚类性能会受到影响，通过信号角度变化剔除发散点可以提高聚类性能[64]，也可以通过密度聚类方法提高聚类中心的估计精度[22]。

估计出混合矩阵以后，考虑信号的稀疏性，源信号可在最小化源信号范数情况下恢复，如式(14)所示[19-21]。

式(14)是典型的线性规划问题，求解方法比较成熟，本文不再赘述。

文献[50]利用通用软件无线电设备（USRP,universal software radio peripheral）构建了原型系统，对天线发射和接收信号进行了多通道盲源分离实验，在干扰信号带宽覆盖通信信号带宽且干扰信号功率大于通信信号功率的情况下，采用盲源分离技术较未采用盲源分离技术的抗干扰能力提升20 dB 以上。在实际工程中，盲源分离抗干扰性能的提升还将受到诸多非理想因素的限制。

2.2 单通道盲源分离抗干扰技术

由于大量通信设备仅设置单根天线，多通道盲源分离抗干扰技术难以直接适用，单通道盲源分离抗干扰技术的需求十分迫切，但技术难度显著增大。

2.2.1 单通道盲源分离基本思路

加性信道情况下，单通道接收混合信号可写成

其中，s(t)为通信信号，J(t)为干扰信号，n(t)为噪声，a和b分别为通信信号和干扰信号的衰减系数。为便于分析，此处未考虑多径的情况。式(15)表明，单通道盲源分离本质上是极端欠定方程的求解问题，旨在利用有限已知量x(t)求解较多未知量(s(t),J(t))，难度极大。由于问题本身的复杂性，单通道盲源分离目前还尚未形成统一的理论框架，学术界主要针对特定场景提出了一些针对性解决方案。对于通信抗干扰场景，本文主要关注利用信号变换域差异的单通道盲源分离技术。

对于国有企业来讲，一定要把企业产权的边界划分清楚明了，这样一来会使得企业对利润的分配更加合理科学，提高企业的资本利用率。此外还要注重塑造银行和企业之间的关系，使得两者之间的信用契约关系稳固坚定，进而形成对企业产生一种牵制作用。

单天线接收的多个信号在时域和频域都相互混叠，但只要各信号在变换域互不重合即可进行分离[65]。因此，可利用信号在变换域的差异构建出多个虚拟观测信号，使混合情况变为适定甚至超定，为信号分离创造条件，主要思路如图5 所示。

图5 中，通过单路混合信号构建出多个虚拟观测信号，进而可利用多通道盲源分离技术实现信号分离[27,66]。

目前，循环平稳[67-69]和经验模态分解（EMD,empirical-mode decomposition）[70-71]等信号处理方法为虚拟观测信号构建提供了理论基础。

2.2.2 基于循环平稳的虚拟观测信号构建

如果随机过程x(t)的自相关函数具有周期性，则x(t)为循环平稳随机过程[67]。即

其中，*表示共轭，E[·]表示数学期望。对Rx(t,τ)进行傅里叶级数展开，可以得到[67]

其中，傅里叶系数可表示为

②仅当循环频率α=0时，高斯白噪声的循环谱非零。

③循环谱由载频、符号速率和调制方式等参数决定。

其中，⊗表示卷积运算。通过求解式(22)所示的线性方程，使(t)和s(t)的误差最小，即可求得LCL-FRESH 滤波器所有参数[69]。

2.2.3 基于EMD 的虚拟观测信号构建

经验模态分解（EMD）是处理非线性非平稳信号的有效手段，无须预先指定基函数即可自适应地将信号拆分成若干个本征模函数（IMF,intrinsic-mode functions）。由于各IMF 包含原信号不同时间尺度的局部特征信息，EMD 能够获得信号的时-频-能量细节表征[70]。

对混合信号x(t)，令第一个分量h0=x(t)，EMD首先构建其上包络和下包络，得到平均包络信号m1，从x(t)去除m1得到第一个分量h1[71]

将h1作为信号，重复上述去除平均包络的过程。定义标准偏差Γ为

当Γ小于给定的阈值时，即得到第一个IMF，记为c1[71]。

得到c1以后，用信号x(t)减去c1，继续上述步骤，当最后的IMF 足够单调时迭代结束。因此，原信号即全部IMF 和残差rn之和，即[71]

由此，原信号x(t)可分解为K个IMF 和一路残差，各IMF 中含有不同程度的s(t)和J(t)，实现了多个虚拟观测信号构建。

上述方法为单通道盲源分离创造了条件，但是，为达到通信抗干扰要求，该类方法的分离精度和计算复杂度还需进一步优化。与多通道盲源分离技术相比，单通道盲源分离理论还未成熟，当前所能达到的技术性能与多通道盲源分离相比还存在差距，需要予以更多的关注。

3 盲源分离通信抗干扰技术的主要特点

3.1 抗宽频段压制干扰

盲源分离利用通信信号和干扰信号的统计域特征差异进行信号分离，在传统空域、频域、码域、时域等抗干扰技术架构基础上，增加了统计域维度。对于宽频段压制干扰甚至全工作频段压制干扰，传统抗干扰技术将面临无频可用且难以硬抗的被动局面。但是，在接收端未饱和溢出情况下，盲源分离依然可实现通信信号和全压制干扰信号分离，从而为对抗极端恶劣干扰提供一种有效手段。

3.2 缓解频谱资源与抗干扰能力之间的固有矛盾

扩谱技术（跳频、直接序列扩谱等）是当前国内外通信抗干扰的主流技术手段，其抗干扰能力以频谱资源为代价[1]。随着用频装备和用频需求不断增加，频谱资源日益紧张。香农公式表明[72]，抗干扰能力不能随着带宽增加而无限制增加，频谱资源的有限性还限制了扩谱抗干扰能力的进一步提升。盲源分离抗干扰技术具有“容扰”的特点，可实现通信信号与干扰信号共存。盲源分离抗干扰技术能够在不增加频谱资源的条件下明显提高通信抗干扰能力，为缓解频谱资源与抗干扰能力之间的固有矛盾提供了一种有效的解决方案。

3.3 节省勤务信令开销

智能抗干扰技术通过智能认知、智能决策、波形机动和频谱机动等步骤，根据电磁环境变化自动调整通信参数来提高抗干扰能力[3]。一般来说，通信双方采取相同的通信参数才能正常通信，因此，智能抗干扰需要交互勤务信令以确保收发端同步调整。点对点通信中，上述信令交互问题尚不明显。但是，在大规模自组织网络情况下，多节点间交互干扰认知结果和协调抗干扰策略将造成大量信令开销。干扰严重时需要更多的信令交互，然而受扰信道又难以提供更多的时频资源。盲源分离在接收端的信号层面进行盲处理，几乎不需要与发送端交互信令，可节省勤务信令所需的系统开销。

3.4 具有内生抗干扰属性

盲源分离性能主要受源信号的相关性影响，几乎不受载频、带宽、调制方式等因素影响。因此，盲源分离对宽频段阻塞、梳状阻塞、扫频等常见干扰具有较好的适应性，不依赖电磁环境感知结果进行调整。盲源分离抗干扰技术在信号空间增加了统计域维度，符合“N+1”维的内生抗干扰框架[3]。

4 下一步发展重点

4.1 解决模型理想化问题

传统盲源分离在源信号统计独立情况下发展起来，目标函数多数以独立性或非相关性为准则。但是，实际应用中，无线通信还可能面临跳频跟踪干扰和直扩相关干扰，其波形与通信信号具有很强的相关性[1]，源信号统计独立的假设前提不再成立，即已有的盲源分离方法难以抗相关干扰。

另外，盲源分离的混合模型过于理想，主要以线性瞬时混合模型和卷积混合模型为主，未考虑电波的大尺度和小尺度模型，尤其是城市、郊区、丘陵等地形地貌对信号的影响。

深度神经网络能够从原始数据中提取复杂特征，还可实现复杂的非线性系统建模，已经成为信号处理的有力工具[28-29,73]。深度神经网络能够深入挖掘信号和信道的细节特征，可为相关信号和复杂信道混合信号分离[74]提供解决方法。

神经网络的深度和训练数据的广度还可弥补单通道盲源分离维度的不足，近年来，基于深度神经网络的语音信号单通道盲源分离研究取得了较大进展[30-31]，可进一步提高无线信号单通道盲源分离技术性能[75]。

4.2 降低处理时延

传统超定和适定盲源分离利用多通道数据估计高阶积累量或非线性函数，涉及大量矩阵和高阶运算，计算复杂度较高。欠定盲源分离通常对信号进行短时傅里叶变换和逆变换以及聚类运算，计算复杂度进一步增加[18-22]。基于粒子滤波的单通道盲源分离技术需要对未知变量的后验概率分布进行蒙特卡罗采样，在粒子多样性匮乏时还需要重采样，计算复杂度太大[25]。基于深度神经网络的单通道盲源分离在训练阶段需要大量的卷积和梯度运算，计算复杂度随网络规模增大而大幅提高[30-31]。随着复杂度不断增加，盲源分离算法的处理时延也相应增加，满足高速无线通信实时性要求的压力越来越大。

光器件具有超大带宽、低功耗和极低时延等优点[57]，可为实时盲源分离提供新的技术支撑。近年来，光器件信号处理获得巨大突破，实现了光子神经网络深度学习的原位反向传播[76]，开发出基于卷积神经网络的硅基集成光子处理器[77]，验证了光学卷积处理器对手写数字的分类能力[78]，实现了50 GBaud/s 的光信号盲源分离[57]，提高了病态混合情况下的分离信号信干比[79]。

上述工作为光器件盲源分离创造了有利条件，为盲源分离在超大带宽和超高速率无线通信场景下的抗干扰应用奠定了基础。但是，光模拟运算及光神经网络还面临着低精度和噪声累积条件下的高准确率计算等问题[80]。

4.3 提高信号分离精度

分离精度直接影响抗干扰效果，盲源分离抗干扰对分离精度的追求没有止境。在强干扰情况下，通信信号功率远小于干扰信号，分离矩阵的微小偏差可能会使通信信号出现较大损失，残留干扰仍将对通信性能造成不利影响。如干信比为20 dB 时，即使99%的干扰成分得到了分离，1%残留干扰的功率仍然与通信信号相当。因此，在强干扰条件下，特别需要关注信号高精度分离问题。

无线通信收发双方共享跳频图案、调制方式、信息速率、载频等先验信息。通信过程中，导频、同步等信号还可实时提供额外的先验信息。在信号处理领域，随着先验信息的增加，估计和求解的精度将随之提升。如果能够利用先验信息设计高精度半盲分离算法，以进一步提高抗强干扰的能力，对无线通信抗干扰具有非常重要的意义。但是，传统盲源分离从“盲”的角度建立起来，如何打破全盲的理论框架，使先验信息的利用成为可能，是需要重点研究的问题。

5 结束语

盲源分离抗干扰技术具有不增加频谱资源和节省勤务信令开销等独特优点，实践表明，在已有抗干扰手段基础上，可进一步提升抗干扰能力。盲源分离抗干扰技术体系已经建立并取得一些实用化成果，但在模型构建和实时性、精确性等方面还面临一些新的挑战。后续研究需要关注基于深度学习的单通道盲源分离、光器件盲源分离和半盲源分离等技术，为盲源分离抗干扰提供新的能力增量。同时，还需要推进盲源分离抗干扰技术与智能抗干扰技术联合设计，以进一步提高无线通信的系统抗干扰能力。