基于多智能超表面的信道空间内生抗干扰方法

朱勇刚，孙艺夫,2，姚富强，李程，郭文龙，安康

（1.国防科技大学第六十三研究所，江苏 南京 210007；2.国防科技大学电子科学学院，湖南 长沙 410073）

0 引言

抗干扰是保密无线通信与一般无线通信的根本区别之一[1]。到目前为止，通信抗干扰技术主要经历了常规扩谱抗干扰和智能抗干扰2 个发展阶段。其中，常规扩谱抗干扰技术以香农信息论为基础，通过扩展通信信号频谱来分散干扰方的干扰功率；智能抗干扰技术遵循“敌变我变”策略，在精确认知干扰信号的基础上，有针对性地动态调整通信信号参数，以适应变化的干扰环境。常规扩谱抗干扰和智能抗干扰都是通信抗干扰方在有限的通信信号空间内与通信干扰方的对抗博弈，主要差别在于两者的智能化程度有所不同。然而，随着干扰变化规律和电磁环境的日益复杂，现有抗干扰技术遇到了性能提升的瓶颈，例如，当干扰信号的维度和功率充满整个通信信号空间时，上述2 种抗干扰方法将失效。文献[2]通过重新审视无线通信系统的构成，提出了无线通信内生抗干扰的概念，即无线通信系统中能够挖掘和利用的内生抗干扰属性主要包括语义空间、通信信号空间和通信信道空间，通过构建动态异构冗余的抗干扰空间，使无线通信系统具备自身鲁棒的先天免疫能力，从而在不需要精确认知干扰的条件下，有效抵抗各种已知或未知干扰的影响，为突破现有无线通信抗干扰性能的瓶颈提供了方向，也为无线通信抗干扰理论与技术发展提供了丰富的想象空间。

近年来，由于智能超表面（RIS,reconfigurable intelligent surface）可为构建智能无线环境带来可能，因此作为6G 候选技术受到广泛关注[3-5]。智能超表面由大量精心设计的电磁单元组成[6]，通过对电磁单元上的可调元件施加控制信号，可以动态控制电磁单元的电磁性质，进而对空间电磁波进行智能调控，形成幅度、相位、极化和频率等参数动态控制的电磁场。在一般无线通信应用中，RIS 主要用于增大信号覆盖范围、热点增流、安全通信和频谱共享等。在保密无线通信应用中，智能超表面为开发和利用通信信道空间，进而实现通信信道空间内生抗干扰提供了基本手段[2]。需要指出的是，与一般无线通信相比，RIS 在保密无线通信抗干扰中的应用至少存在以下两点区别：一是作为非合作方，干扰方到接收机和RIS 的信道信息往往难以准确获取，这给RIS反射系数的优化带来困难；二是为了获得足够的“信道维”内生抗干扰能力[2]，必须尽可能开发和利用信道空间，即研究多RIS 辅助的通信抗干扰方法，然而，现有基于单RIS 的通信抗干扰方法难以扩展到多RIS 的场景[7-11]。

针对基于单智能超表面的抗干扰应用场景，文献[7]提出了一种低复杂度解码算法，以及RIS 反射系数和发射功率交替优化方法。文献[8]分析了RIS单元个数对多用户通信系统性能的影响，结果表明，当单元个数大于2K(K-1)时，RIS 能够有效降低多个用户之间的互扰。文献[9]提出了一种基于发射波束和RIS 相移联合优化的抗干扰方法。在此基础上，文献[10-11]进一步研究了同时存在干扰和窃听攻击时，基于RIS 的无线通信系统性能。但是，以上文献假设通信抗干扰准确已知干扰功率或干扰信道等信息，该假设在实际应用中往往难以成立。文献[12-13]分别研究了存在干扰感知误差和干扰来波方向不确定条件下的RIS 参数优化与调控方法。文献[14]研究了干扰与通信信号之间的相关性对通信系统性能的影响，结果表明，当干扰信道与通信信道之间的空间相关矩阵渐进正交时，接收机信噪比与智能超表面单元数的二次方成正比；否则，接收机信噪比与智能超表面单元数呈线性关系。因此，为了充分挖掘信道空间内生抗干扰能力，还需重点研究分布于电波传播环境中不同位置的多个RIS 对抗干扰性能的影响[2]。在基于多RIS 的无线通信系统模型和性能研究方面，文献[15]分析了多RIS 辅助通信系统，提出了从多个RIS 中选择一个最优RIS 用于辅助通信时的等效信道模型，结果表明，上述2 种情形都可以采用Gamma 分布和Log-Normal 分布有效刻画等效信道系数。文献[16]分析了由2 个RIS 构成的并联信道和级联信道的传输模型，验证了多RIS 能够显著改善室内、室外等场景下的误码性能和可达速率。文献[17-18]分别研究了多RIS 辅助的通信系统以及从多个RIS 中选择一个最优RIS 用于辅助通信的系统性能，结果表明，在发射功率一定的前提下，多RIS 辅助的通信系统误符号率显著低于无RIS 辅助的通信系统，且随着RIS 个数和RIS 的单元个数增加而减小。通过在RIS 中嵌入主动单元，文献[19]提出了一种从多个RIS 中选择一个最优RIS 用于辅助通信的方案。然而，目前还未见基于多RIS 的通信抗干扰研究报道。

本文将RIS 的应用扩展到无线通信抗干扰，提出了一种基于多智能超表面的信道空间内生抗干扰方法。其基本思路是通过分别优化位于电磁空间中的智能超表面反射系数、发射波束和接收波束，使智能超表面成为增强通信信号和抑制干扰信号的可控信道；通过调整各智能超表面的开关状态，使发射机-RISl(1≤l≤L)-接收机之间构成一种动态异构冗余的无线信道空间，为无线通信抗干扰提供了新的维度。同时，针对干扰信息往往难以准确获取的问题，本文所提方法对不确定干扰信息进行了鲁棒化处理，为实现不以干扰精确认知为前提的抗干扰提供了技术支撑。

1 系统模型

本文考虑的系统模型如图1 所示。该模型包括一个发射机、一个接收机、一个干扰机以及L（L≥ 1）个开关状态受发射机控制的智能超表面。假设发射机与接收机之间直射链路受阻，且发射机和接收机分别配备NT根和NU天线，第l（1≤l≤L）个智能超表面含有NR,l个反射单元并与一个开关控制器相连，发射机可以通过开关控制器来控制RISl的工作状态xl∈{0,1}，其中，“0”表示RISl关闭，“1”表示RISl开启。

图1 多智能超表面辅助的通信抗干扰系统模型

由式(1)可知，接收机接收信干噪比为

与现有基于多RIS 辅助的无线通信系统模型[15,17]相比，图1 所示的系统模型主要存在两点区别：一是考虑了干扰的影响；二是在每个智能超表面中增加了开关状态控制变量xl。理论上，通过优化智能超表面的相移矩阵Pl，发射机-RISl-接收机之间将构成一条可控的无线信道；通过动态调控各智能超表面的开关状态xl，可在收发两端生成多条可控的无线信道，当各信道之间的相关性足够弱时，则可以构建可控的动态异构冗余信道空间，为信道空间内生抗干扰提供支撑[2]。

在上述模型中，智能超表面的优化和调控不可避免地受到干扰的影响，然而，由于干扰机与通信方之间的非合作关系，干扰信道信息往往很难被准确获取，因此，如何在干扰信息不确定性条件下对多智能超表面进行优化和调控成为问题的关键。为此，本文将不确定性干扰建模为干扰机与接收机和干扰机与RISl之间的信道hJ和gJ,l的不确定性区域[11]，即

其中，θ,φ分别为信道的方向角和仰角，(θL,φL)和(θU,φU)分别为对应角度的上下限，也即将干扰建模为位于Δ 范围内的随机变量。值得注意的是，本文仅需获取干扰信道仰角和方向角分布范围作为先验信息，不需要获取干扰样式等其他干扰参数。由此，基于智能超表面的抗干扰问题转化为在干扰信息不确定性区域Δ 条件下和满足最大发射功率、RIS 幅度和接收波束等约束下，联合优化发射波束f、接收波束v和智能超表面相移矩阵Pl及其开关状态xl，使频谱效率最大化，即

其中，C1 为发射机功率约束，Pmax为最大发射功率约束；C2 为智能超表面相移矩阵幅度约束；C3 为接收机天线波束幅度约束；C4 为智能超表面工作状态约束。

2 多智能超表面的优化与选择算法

本节提出了一种基于块坐标下降（BCD,block coordinate descent）的低复杂度算法求解式(4)，即通过对干扰信息不确性区域Δ 离散化处理得到鲁棒干扰信道，然后采用交替优化方法将多个优化变量解耦并分别优化得到对应闭式解，最后利用贪婪算法优化RIS 开关变量。

2.1 不确定干扰的鲁棒化处理

为将含有不确定性区域Δ 的难以求解的优化问题式(4)转化为可求解的问题，本节将Δ 离散化为S（S〉 1）个样本集合，定义为[11]

当S→∞时，离散化的逼近于连续的Δ。此时，在干扰信息不确定性区域Δ 内的任何干扰产生的信道矩阵均可以由中元素的线性组合表示。进一步将式(3)中矩阵元素的方向角与仰角均匀离散化

2.2 多智能超表面相移矩阵与收发射机波束优化

本节主要给出基于循环坐标下降（CCD,cyclic coordinate descent）法[20]的多智能超表面相移矩阵优化算法，以及发射波束和接收波束的最优闭式解。需要指出，尽管半正定松弛（SDR,semidefinite relaxation）[21-22]、连续凸优化（SCA,successive convex approximation）[23]等通用的优化方法也可对本节中的优化变量进行求解，但上述方法往往需要引入大量辅助变量进行近似处理，计算复杂度较高[24-25]。

交替更新η和，可以得到多智能超表面相移矩阵的最优闭式解。

其次，优化发射波束f。结合式(2)和式(4)可知，使频谱效率最大的发射波束是使式(2)的分子最大的发射波束。因此，在发射功率约束条件下，容易得到发射机的最佳发射波束为

最后，优化接收波束v。结合式(2)和式(4)，可以得到最小均方误差准则[27]下的接收波束v最优闭式解为

2.3 多智能超表面的选择

在优化智能超表面相移矩阵Pl、发射波束f和接收波束v之后，问题式(4)转化为以多智能超表面开关状态为变量的非线性整数优化问题。一般地，非线性整数优化问题是NP-hard 问题，难以得到全局最优解。本节给出一种贪婪的多智能超表面选择算法，如算法1 所示。其基本思路是首先开启所有智能超表面，然后逐个关闭智能超表面RISl，并比较关闭前后的目标函数，用以判断开启该智能超表面是否有利于抗干扰，直至遍历所有智能超表面。

算法1贪婪的多智能超表面选择算法

算法1 中，步骤1)初始化RIS 的开关矩阵x；步骤4)计算关闭RISl后的目标值γl；步骤5)比较新的目标值与初始目标值的大小，如果k≠0，表示关闭RISk可以获得更高的频谱效率提升，然后令xk=0，并更新下一次迭代的初始值，如果k=0，这意味着关闭任何一个RIS 都不可能提高频谱效率，此时需要终止循环并输出最优开关矩阵x。

最后，给出本文所提方法的整体流程，如算法2所示。

算法2基于多智能超表面的信道空间内生抗干扰方法

算法2 中，步骤1)初始化RIS 相移矩阵P0、发射机波束f0、接收机波束v0、开关状态xl，并定义误差ξ；步骤3)和步骤4)根据CCD 算法、发射机波束和接收机波束的闭式解、算法1 以及目标函数式(7)不断更新P,f,v,x,γ，直到γ收敛时输出P,f,v,x的最优解。

3 收敛性和复杂度分析

本文所提方法对智能超表面相位矩阵采用迭代优化方法求解，因此需分析其收敛性。本节通过证明η与Pl的单调性推导出递增收敛至式(9)的KKT 解。

其中，不等式(a)因η的更新而成立；等式(b)和不等式(c)因优化Pl而成立；不等式(d)因最大最小问题的下降性质而成立。由此可见，序列是单调递减的。

其次，证明CCD 算法生成的序列收敛至式(9)的KKT（Karush-Kuhn-Tucker）点。对于η的收敛性，用以下的不等式证明，即

不等式(19)因式(16)和优化函数上界性质而成立。当m→∞，结合η的收敛性，可以得出

其中，α是与单位模量约束相关的双变量。最后，结合部分KKT 条件和式(21)，可得

此外，由于约束C1 和C2 的存在，优化框架存在上限，即收敛至最优点。

下面通过算法复杂度来比较所提方法与现有算法的时效性。具体来说，所提方法的复杂度主要来自3 个方面：一是求解式(9)的CCD 算法；二是收发数字波束f和v的计算；三是选择最优智能超表面的贪婪算法。令I1和ε1分别表示所提方法外层循环和CCD 算法的容错精度，由文献[20]可知，更新式(11)中单个i的复杂度为O(NR)，那么求解式(9)的CCD 算法的总复杂度为；接着，由文献[29]可知，通过式(14)和式(15)计算f和v的复杂度分别为 O (NUNR)和O (NTNR)；最后，贪婪算法的复杂度主要来自计算目标函数式(7)，根据文献[29]可得，其总复杂度为 O(L2NTNRNU)。因此，所提方法的总复杂度为

此外，广泛采用的SDR 和SCA 算法与所提方法的区别在于式(9)的求解算法不同，对应的复杂度也不同。对于SDR 算法，求解式(9)的复杂度来自用CVX 工具求解变量为=且具有NR个约束的优化问题，根据文献[10]，其总复杂度为

对于SCA 算法，求解式(9)的复杂度来自用CVX 工具求解具有NR+3个优化变量和NR个约束的优化问题，根据文献[29]，其总复杂度为

4 仿真结果与分析

本节通过数值仿真来评估所提方法的性能。仿真参数设置如下：智能超表面个数L=2，且每个智能超表面的单元数为NR,1=NR,2=64，接收噪声功率δ2=10-11W，发射机和接收机天线数和功率分别为NT=36，NU=16，Pmax=1 W，PJ=20 W。此外发射机、干扰机、RIS1、RIS2和接收机分别部署在（0 m，0 m，100 m），（9 m，9 m，78 m），（18 m，18 m，57 m），（-30 m，30 m，75m），（-4 m，55 m，31 m）。在该位置部署中，RIS1在发射机与干扰机所在直线的延长线上。另外，干扰信道的不确定角度为ϕJ=θU-θL=φU-φL=4°。本文采用文献[11]中的信道模型对干扰信道和合法信道进行建模，即

1) 无RIS 辅助。收发射机之间存在直射链路，且没有RIS 辅助。

2) 多RIS+CCD。收发射机之间无直接链路，但存在多个处于开启状态的RIS，利用CCD 算法优化RIS 相移矩阵的通信场景。

3) 多RIS+CCD+RIS 开关控制（本文所提方法）。收发射机之间无直接链路但存在多个RIS，利用CCD 算法优化RIS 相移矩阵后，再利用RIS 开关优化算法优化RIS 工作状态的通信场景。

4) 单RIS+CCD。收发射机之间无直接链路且只存在单个智能超表面，即RIS1，利用CCD算法优化RIS 相移矩阵的通信场景。为了便于比较，设置此场景下RIS1的单元个数为NR=128。

图2 给出了不同干扰功率下的频谱效率随干扰功率的变化情况。从图2 可以看出，当干扰功率PJ=0时，单RIS+CCD 辅助的通信场景具有最高的频谱效率，但是随着干扰功率的增加，其频谱效率急剧下降，而本文所提方法始终保持较高的频谱效率。这是因为在本文仿真场景下，由于单RIS 只存在一条双衰落路径，且RIS 集中部署单元个数多时，能更好地补偿双衰落。但是当存在干扰时，由于单RIS 场景中干扰信道和通信信道正相关，调节RIS反射波束会同时增强合法通信信号和干扰信号强度，因此通信性能急剧下降。而本文所提方法可以通过调控RIS 开关构建动态异构冗余的信道抗干扰空间，使通信信道与干扰信道不相关，进而优化RIS 波束相位在合法通信信号强度增强的同时零陷干扰信号，从而在高干扰功率下实现鲁棒通信抗干扰。

图2 不同干扰功率下的频谱效率随干扰功率的变化情况

图3 给出了不同RIS 单元个数下不同方法的频谱效率。在该仿真中，NR,1=NR,2=N，对于单RIS+CCD 方法的仿真场景，其单元个数设置为NR=2N。可以看出，本文所提方法的频谱效率远高于其他算法，且其频谱效率随着RIS 单元个数的增加而提升，而其他方法的频谱效率基本保持不变。这是因为发射信号与干扰信号方向一致，RIS 无法分辨信号与干扰，从而无法提升频谱效率，而本文所提方法利用冗余信道空间，通过关闭RIS1，识别发射信号与干扰信号，从而提升频谱效率。

图3 不同RIS 单元个数下不同方法的频谱效率

图4 给出了不同发射与接收天线个数下的频谱效率。从图4 可以看出，所提方法与无RIS 辅助的频谱效率随着发射机与接收机的天线数的增加而增加，且所提方法始终高于其他方法。这是因为增加天线个数能提高阵列增益与分集增益，从而提高频谱效率。但其他对比方法由于无法分辨信号与干扰，频谱效率提升不大。

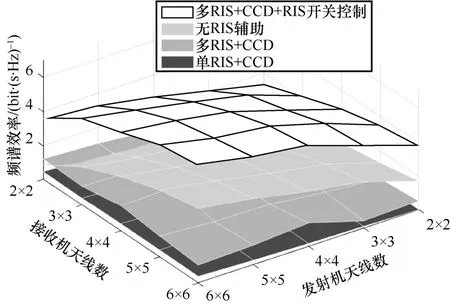
图4 不同发射与接收天线个数下的频谱效率

图5 给出了不同信道不确定度ϕJ下的频谱效率。从图5 可以看出，随着信道不确定度的增加，所有方法的频谱效率几乎没有下降。这是因为所有算法都采用了本文的不确定干扰鲁棒化处理。这说明不确定干扰鲁棒化处理不仅适于本文所提方法，也适用于其他方法，且能够有效降低干扰不确定性带来的影响。

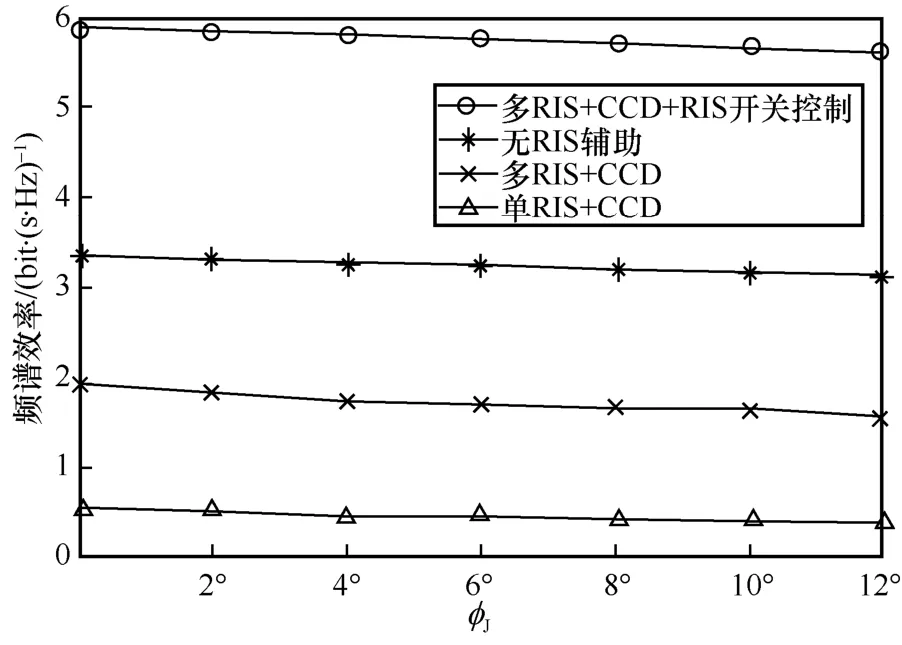
图5 不同信道不确定度 ϕJ下的频谱效率

为了进一步验证第3 节中复杂度分析的正确性和所提方法的时效性，本文采用当前智能超表面系统广泛使用的运行时间作为评判指标来衡量算法复杂度[30]。图6 给出了不同RIS 单元个数下不同方法的运行时间。从图6 可以看出，由于所提方法直接给出了最优闭式解，而常规SDR 和SCA 优化算法需要引入大量辅助变量进行近似处理，因此随着单元个数增加，所提方法所需运行时间缓慢增加（0.3～0.8 s），且与SDR 和SCA 方法运行时间之差急剧增大，这与第3 节中复杂度分析相吻合。上述结果表明所提方法具有较高的时效性，有利于抗干扰性能的提升。

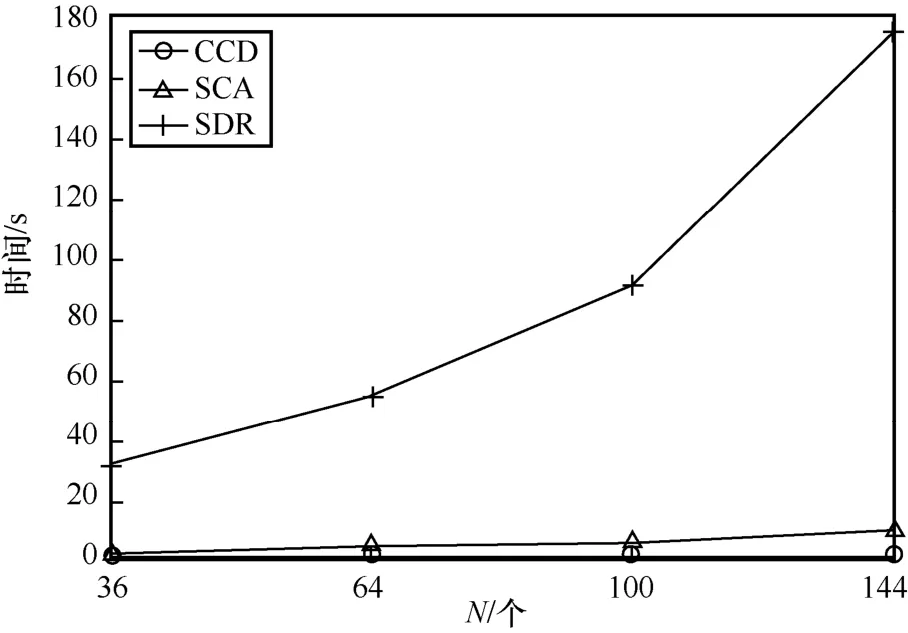
图6 不同RIS 单元个数下不同方法的运行时间

5 结束语

本文提出了一种基于多智能超表面的信道空间内生抗干扰方法，与已有方法相比，所提方法的主要优势是能够在不精确认知干扰的条件下有效抵抗干扰，可用于未知干扰和智能干扰等应用场景，为实现信道空间内生抗干扰提供了技术支撑。理论分析与仿真结果验证了所提方法的有效性。需要指出的是，尽管本文所提方法能够有效抵抗信道信息存在不确定性的干扰，但依然需要已知干扰的变化范围，且对RIS 的调控信息同样面临干扰威胁。下一步需要重点在如下3 个方面展开研究，一是研究不需要任何干扰信息的信道空间内生抗干扰方法；二是将信道空间与信号空间、语义空间相结合，研究多维空间联合的内生抗干扰方法；三是结合实际应用场景设计多RIS 联合调控方法。