基于球域失真空-时依赖的全景视频编码

杨栩，朱策，郭红伟,4，罗雷1,

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.成都师范学院物理与工程技术学院，四川 成都 611130；3.电子科技大学信息与通信工程学院，四川 成都 611731；4.红河学院工学院，云南 蒙自 661100）

0 引言

随着Web3.0 的到来和元宇宙的兴起，虚拟现实（VR,virtual reality）和增强现实（AR,augmented reality）[1]技术为用户提供了沉浸式交互视听体验，广泛应用于游戏、监控、视频会议等领域。相较于传统2D 视频，VR 全景视频[2-3]包含360°×180°的全方位球域视觉信息，具有高分辨率、高帧率以及大视场等特征[4]，数据量极大，这给传输和存储全景视频带来巨大挑战。因此，迫切需要高效的全景视频压缩技术来应对这些挑战。

全景视频投影到编码平面后再使用传统视频编码器（如高效视频编码（HEVC,high efficiency video coding）标准H.265/HEVC[5]、通用视频编码（VVC,versatile video coding）标准H.266/VVC[6]对应的编码器）进行压缩。然而，全景视频在投影过程中会产生边界和拉伸形变，影响跨边界的运动搜索和形变区域的编码性能。因此，在全景视频编码方面，一些研究聚焦于投影格式（如等距柱状投影（ERP,equi-rectangular projection）[7]、正六面体投影（CMP,cubemap projection）[8]、正八面体投影（OHP,octahedron projection）[3]等），以期找到既具有较少的投影边界又能产生较小拉伸形变的投影格式。然而，很难找到能同时满足这2 个条件的投影格式，因为投影平面越少，投影边界越少，但拉伸形变越严重；反之，投影平面越多，拉伸形变越小，但投影边界也越多，导致组合后的矩形编码平面的图像不连续。由于CMP 失真相对较小，正六面体的展开平面能成为一个独立的矩形编码平面，符合编码器基于矩形块划分的编码特性，因此CMP 成为传统编码和智能编码[9]的主要研究对象之一，本文将在CMP 上建立优化模型。

还有一些研究集中在改进编码算法，以弥补投影带来的编码性能损失。一类研究关注投影边界，例如文献[8,10]通过填充CMP 边界区域来提升跨边界运动搜索效果。然而，由于投影边界占比较小，性能提升非常有限，特别是对运动变化不大的全景视频几乎没有效果。在此基础上，文献[11]不仅进行了边界填充拓展，还建立了符合全景视频特征的率失真优化模型，从而提升了编码性能。另一类研究关注投影产生的拉伸形变，文献[12]针对CMP提出基于熵平衡的比特分配算法以匹配拉伸区域的形变程度，进而提升率失真性能。文献[13]根据CMP 在平面中心区域与外围区域的形变程度来调整量化参数（QP,quantization parameter），取得和文献[12]差不多的编码性能。文献[14]根据CMP的形变程度，提出一种球域率失真优化算法。虽然这些算法对全景视频编码比较有效，但是其仅考虑投影区域的拉伸形变对编码性能的影响，没有考虑编码帧间的时域依赖关系，因此率失真性能还有较大的提升空间。

视频编码的帧间预测技术使当前编码单元的失真不仅影响其自身的编码性能，还会影响后续编码帧中参考该单元的编码块的率失真性能，文献[15-20]对2D 平面的时域依赖率失真优化模型进行了研究。但该模型无法直接应用于全景视频编码，并且该模型的复杂度较高，这对超高分辨率的全景视频编码来说是不可行的。

本文针对正六面体投影的全景视频编码，提出空-时依赖的球域失真模型，主要贡献如下。

1) 在CMP 上建立平面编码失真与球域感知失真的空域映射模型。像素均匀分布在整个球面，投影后拉伸平面区域的冗余像素与其面积成正比，以此来划分平面编码区域及球面环带区域并计算相应面积，并将面积比作为球域失真空域映射权重。

2) 根据运动补偿预测的时域参考关系建立球域失真时域传播模型。为了降低编码复杂度和减少缓存空间，建立失真后向传播链。通过运动补偿预测误差和重建误差的关系来计算失真时域影响权重。

3) 根据帧级时域相关性自适应调整帧级量化参数，根据球域失真空域映射权重和时域影响权重来调整编码树单元（CTU,coding tree unit）级拉格朗日乘子和QP。实验结果显示，在相同编码质量下，本文算法在所有全景视频测试序列上有平均超过7%的码率节省。

1 球域失真空-时域依赖优化模型

全景视频需要投影到2D 平面进行编码，解码后反投影回球面供人观看，这种框架使主观视觉感受受到球域失真而非编码失真的影响。然而，客观质量评价受基于均方误差（MSE,mean square error）的编码失真影响。不一致的主客观质量评价会损失编码性能。此外，运动补偿预测误差使球域失真在时域传播，当前编码单元的失真不仅影响自身的编码性能，还会影响后续与它具有参考关系的编码单元的编码性能。针对以上两点，本文提出一种空-时域依赖的球域失真优化模型。

为了使全景视频编码的客观质量评价与主观质量评价保持一致，全景视频在平面编码的率失真优化目标是在给定的目标比特内尽可能地减少球域感知失真而非编码失真，也即

其中，及Ri分别为第i块编码单元所对应的球域感知失真和平面编码比特，RT为编码比特预算，N为编码单元总数。

如图1 所示，球面图像会投影到正六面体的6 个面以适应编码器的矩形图像编码规则。在实际编码过程中，编码器会将编码平面划分为有限个编码单元，并按照行和列排列。根据球面图像到编码平面再到编码单元划分之间的一一对应关系可以看出，每一个编码单元都对应着唯一的一块球面区域。虽然像素点均匀分布在整个球面，但是不同位置的球面图像到编码平面的投影距离不同，导致与每个编码单元对应的球面图像在投影后会出现不同程度的拉伸形变，拉伸区域的空缺像素通过插值填充，但这些插值像素并不真实存在，而是成为冗余像素并对编码域的主客观质量评价产生影响。

图1 全景视频正六面体投影

为了使影响球域主观质量的评价指标球域失真和编码域的质量评价指标编码失真Di趋于一致，引入编码单元的空域映射权重来抵消冗余像素对编码域编码失真的不利影响。所以，CMP 视频序列的平面编码失真与球域感知失真之间存在以下映射关系

其中，和Di分别为第i个编码单元所对应的球域失真映射权重以及编码失真。

根据拉格朗日乘子法[18]，合并式(1)和式(2)，将约束性优化问题转换为无约束优化问题，则球域率失真优化模型变为

其中，λ为全局拉格朗日乘子，用于平衡失真和码率，较小的λ使失真较小但消耗的码率较大，较大的λ使失真较大但消耗的码率较小；o1,...,oN为编码单元的编码参数，比如量化参数、编码模式、参考帧索引等。由于编码参数之间存在耦合关系，因此式(3)的全局率失真优化问题在编码中难以实现。

视频编码采用独立率失真优化技术，其易于实现且复杂度较低。编码时，假设编码单元间相互独立，对每个编码单元进行独立率失真优化。当前编码单元的率失真性能仅取决于当前编码单元的编码参数，与其他编码单元的编码参数无关，即

其中，λi及oi分别为当前编码单元的拉格朗日乘子及编码参数。然而，独立率失真优化使编码性能还有很大的提升空间。

根据文献[18]，编码单元的码率仅由其自身的编码参数决定，而失真与其参考单元的失真具有很强的相关性，失真会通过运动补偿预测在时域传播。所以，有必要建立失真传播链并量化失真的影响大小。

除非场景切换，视频图像具有时域连续性。帧间预测技术充分利用这种特性来减少视频信号在时域上的冗余，进一步提高了压缩率。已编码单元的失真会影响后续以其为参考的编码单元的失真，从而形成一条失真时域传播链，如图2 所示。图2(a)为球域失真传播链；图2(b)为球面图像投影到六面体后的失真传播链；图2(c)为编码平面上的失真传播链。

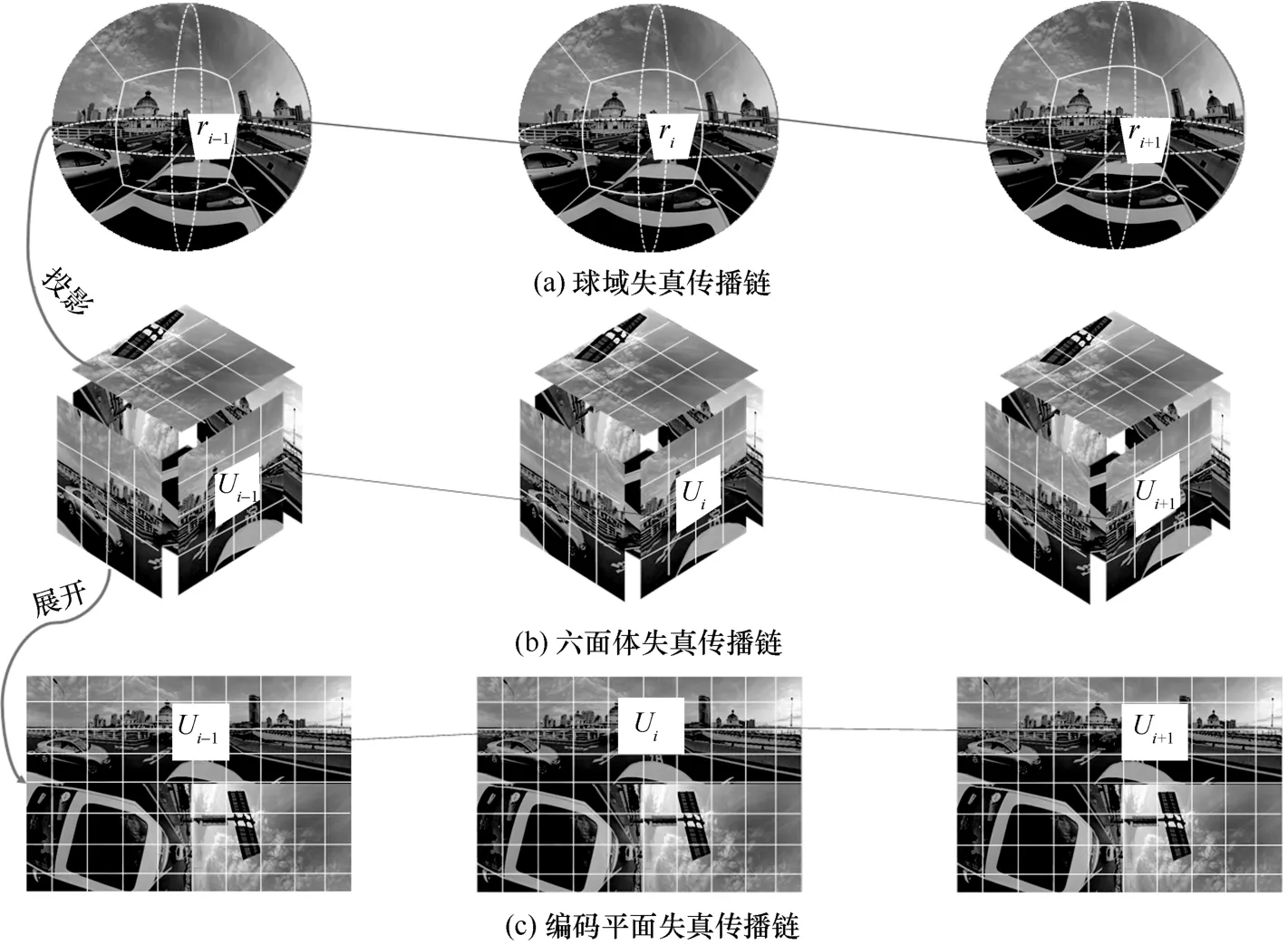
图2 失真时域传播链

根据文献[18]，失真时域传播链上第i+1 个编码单元Ui+1的重建失真Di+1和运动补偿预测（MCP,motion compensation prediction）失真存在如下关系

其中，b为与视频信号源相关的常量；Ri+1为编码码率，主要由自身的编码参数决定。可以表示为

依次类推，传播链上第N个编码单元的失真DN与Di的关系可以表示为

结合式(5)～式(8)，式(3)中的球域率失真优化问题变为

式(9)的球域率失真优化模型进一步表示为

2 球域失真空域映射权重

不同经纬度的球面区域到正六面体的投影距离不同，导致球面区域投影到平面后出现不同程度的拉伸形变。具体而言，具有相同弧度ϕ的不同位置球面区域在平面上的投影高度会有所差异，如图3 所示，CMP 的切面上高纬度球面区域在投影平面的高度d1大于低纬度区域投影高度d2。投影后，通过插值来填补平面拉伸区域的空缺像素，而插值的冗余像素会影响全景视频的编码性能。为解决这个问题，本文需要在球域失真与编码失真之间建立一个符合主客观质量评价一致性的空域映射模型。

图3 同弧度球面投影高度变化

从六面体的一个面来观察，可以看到球面图像的一部分被投影到该面上。如图4 所示，黑色正方形块为投影平面，球面区域被划分为5 个环带区域，每个区域宽度相同，分别标记为1～5。假设球面上同一环带区域到投影平面的距离相等，相应区域的各编码单元的失真权重相同。由于像素点在整个球面上均匀分布，球面图像投影到编码平面前后的像素点数量与区域面积成正比。因此，本文用面积比来量化球域失真映射权重。

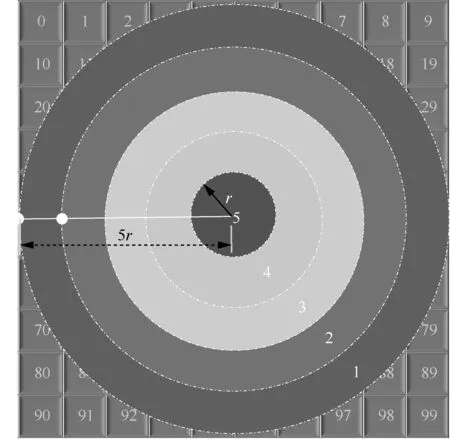
图4 球面区域划分

由于CMP 的6 个投影平面的分辨率相同，均为1 280×1 280，将其划分为100 个分辨率为128×128 的CTU。为了与编码平面对应，将球面环带宽度r设定为CTU 的行宽。则第i个球面环带区域面积Ssphere(i)为

在编码平面，各编码单元对应着唯一的球面区域，将编码平面划分为与球面环带区域对应的5 个编码平面区域，分别标记为数字1～5，如图5 所示，同色的编码单元组成同一编码平面区域，同一编码平面区域的球域失真映射权重相同。

图5 编码平面区域划分

第i个编码平面区域面积Scmp(i)为

因此，根据式(11)和式(12)，第i个编码平面区域内的编码单元的球域失真映射权重为

至此，对于正六面体的一个编码平面的球域失真映射权重模型已经建立，而实际编码平面包含6 个映射平面，将它们按照如图6 所示的顺序排列，从而组成一个矩形编码平面。图6(a)展示了投影平面的组合顺序，编码平面的第一行分别为左、前、右投影平面，第二行分别为底、后、顶投影平面。图6(b)展示了编码平面的区域划分，而该区域划分方式决定了编码单元的空域映射权重。

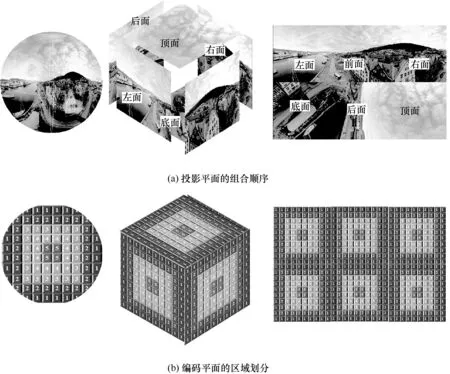
图6 投影平面的组合顺序和编码平面的区域划分

3 球域失真时域影响权重

球域失真映射到编码平面后，由于采用了帧间预测编码技术，编码平面上的压缩失真不仅影响当前编码单元的编码性能，还会对后续参考该编码单元的其他编码单元的编码性能产生影响。因此，当考虑时域依赖编码时，需要根据参考关系来建立全局率失真优化模型。最新的通用视频编码标准VVC 采用层次编码结构，如图7 所示，其中8n+i表示第n个图像组（GOP,group of picture）中每个编码帧的图像序号（POC），i=1,2,…,8。在低时延编码配置中，一个GOP 包含8 帧，分为3 层。编码帧参考时域上前一帧以及最近邻的3 个关键帧，当前编码帧的失真会在时域上进行传播。因此，有必要量化编码单元的失真影响因子，并根据该失真影响因子来调整编码参数，从而提升传播链上所有编码单元的整体编码性能。

图7 层次编码结构

根据式(5)～式(8)，可以递推出当前编码单元的失真影响因子，然而，该失真影响因子的求解需要缓存未编码帧，并通过前向运动搜索在源像素上来完成，复杂度极高。为了不增加编码复杂度，根据视频信号连续性特性，可以在已编码帧上建立后向失真传播链，如图8 所示，根据已编码信息来量化失真影响权重。

图8 后向失真传播链

根据式(5)～式(7)，在后向失真传播链中，当前编码单元Ui的失真Di与前一编码单元Ui-1的失真Di-1之间的关系变为

同理，当前编码单元Ui的失真Di对后向失真传播链中编码单元Ui-N的失真影响变为

根据式(14)可得，失真影响因子βi-1为

当编码图8 所示的传播链上的编码单元Ui时，后向传播链上的其余编码单元已经完成编码，所以式(16)中Di-1及可以获取。进而式(9)变为

综合式(15)～式(17)，编码单元Ui的失真时域影响权重为

4 算法实现

第2 节和第3 节根据第1 节建立的球域失真空-时域依赖模型确立了球域失真空域映射权重和时域影响权重，它们在算法实现过程中会调整拉格朗日乘子和量化参数，从而影响编码模式的选择以及编码失真。因此，算法实现过程中需要调整量化参数。

4.1 帧级量化参数调整

当前主流编码器均采用图7 所示的层次编码结构，将一个GOP 中的各帧分成不同的编码层次，不同层次的编码帧采用不同的编码策略，QP 级联编码策略[21]作为一种重要的层次编码技术，极大地提升了编码性能。然而，当前QP 级联技术采用固定的QP 偏移策略，即

其中，QPslice为帧级量化参数；QP0为编码器默认的输入量化参数；QPi为第i层编码帧的量化参数偏移量，层次越高，该偏移值越大。

虽然该技术能体现不同层次编码帧的重要性，却不能根据图像特征自适应调整量化参数。为此，本文提出一种自适应帧级QP 调整策略。

自适应量化参数编码策略是根据帧级时域依赖性的大小来调整量化参数。直观上讲，对于时域相关性较强的编码帧，有大部分编码单元采用帧间预测编码，极限为当前编码帧的失真完全由参考帧决定；反之，则可能有较多的编码单元采用帧内预测编码。所以，可以通过帧级重建失真误差与运动补偿预测误差的比值来量化帧级时域相关性。然而，在编码某帧结束之前不能获取重建失真误差与运动补偿预测误差信息，也就不能量化该编码帧与参考帧的时域相关性大小。为此，根据视频图像的连续性特点，只要没有发生场景切换（在实际编码过程中，使用帧像素值的方差的变化量来判断视频场景是否发生切换），就可用时域邻近已编码帧的编码信息来近似量化当前编码帧的时域相关性大小，即

其中，ωslice为帧级时域依赖权重，分别为当前编码帧的上一帧的重建失真误差和运动补偿预测误差，Om,n、Cm,n和Pm,n分别为源像素值、重建像素值和预测像素值，H和W为图像分辨率的高和宽。

为了保证关键帧的参考质量，帧级量化参数调整策略仅用于时域相关性较强的非关键帧，即

4.2 编码树单元级量化参数调整

将式(10)中的带权重的拉格朗日乘子表示为当前编码单元Ui的拉格朗日乘子λi，也即其率失真曲线斜率为

其中，λ为参考软件本身的拉格朗日乘子，由帧级量化参数计算而来，即

其中，QPslice为4.1 节优化后的帧级量化参数，ωl为与编码帧所属层级相关的权重系数，ξ为与当前编码帧是否作为参考图像相关的系数。

由式(22)计算出每个CTU 的拉格朗日乘子后，再使用文献[22]拟合的拉格朗日乘子与QP 的关系式计算QP 并用于编码，即

4.3 算法流程

本节给出球域失真空-时域依赖的球域率失真优化（STD-SRDO,spatial and temporal dependent based spherical rate-distortion optimization）算法的详细流程，如算法1 所示。该算法在空-时域依赖的球域失真模型上分别进行帧级和编码树单元级量化参数调整，通过球域失真映射模型获取球域失真空域映射权重，再通过球域失真时域传播模型获取失真时域影响权重，最后计算拉格朗日乘子和量化参数以优化编码。假设编码帧数为N，每帧包含M个编码单元。

算法1球域失真空-时域依赖的球域率失真优化

5 实验

全景视频编码的目标是在最小化码率和编码时间的同时，保证编码质量。为验证本文算法的有效性，将基于球域失真空-时域依赖的全景视频编码算法集成到VVC 参考软件VTM14.0 中，编码器配置为低时延P 帧（LDP,low-delay P frame）和低时延B 帧（LDB,low-delay B frame），实验条件遵守国际编码标准组织（JCT-VC,joint collaborative team on video coding）建议的通用测试条件（CTC,common test conditions）[23]，全景视频编码的标准测试序列包括8K、6K 和4K 三类共计16 个视频序列，其帧率、比特深度以及分辨率等特征信息如表1 所示。实验计算机配置为Intel(R) Xeon(R) Platinum 8255C CPU @2.50 GHz×2，内存为256 GB，基于X64 的处理器，64 位Windows10 专业版操作系统。

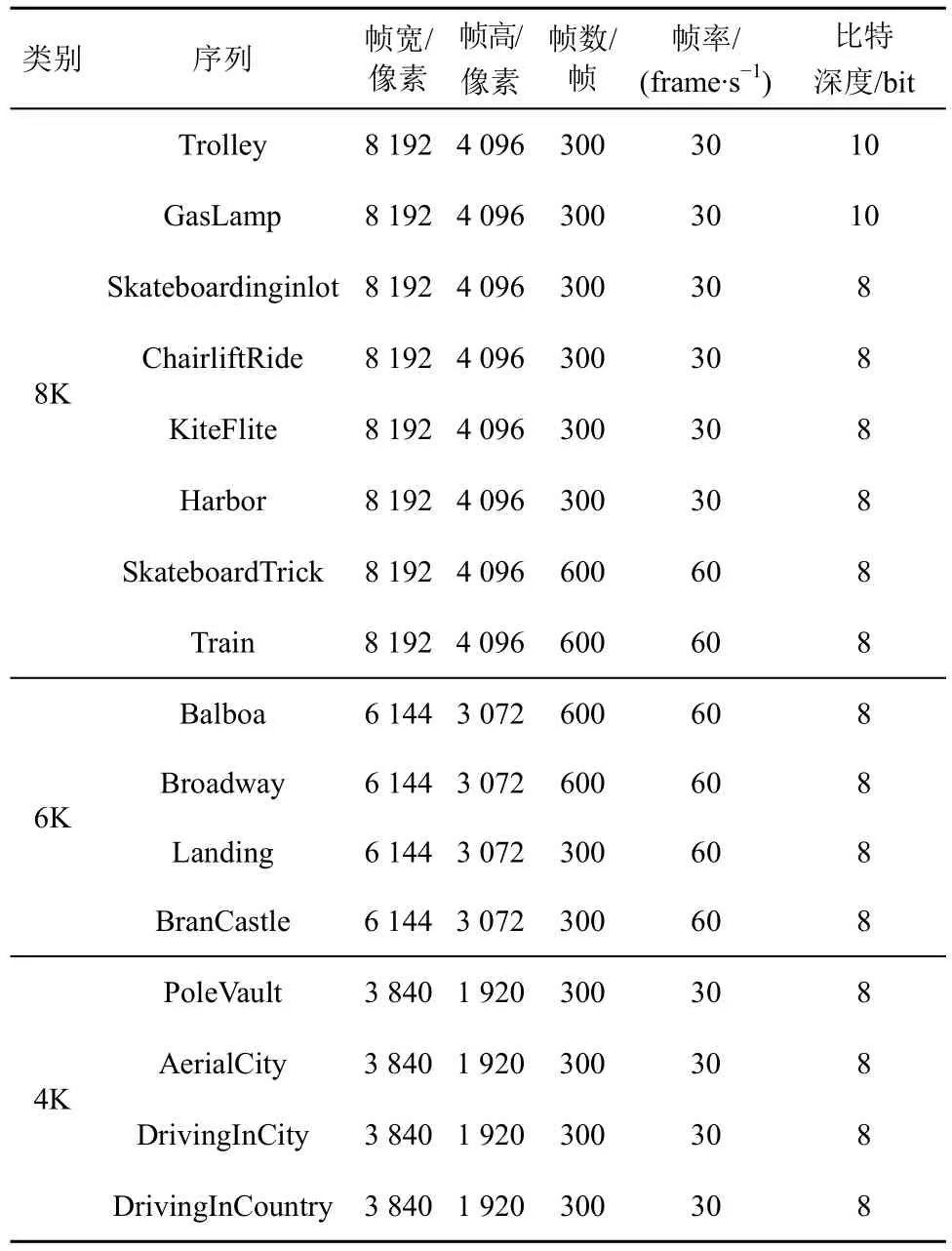
表1 全景视频测试序列特征信息

全景视频大都具有较多的仿射运动，运动目标通常出现在赤道区域附近[24]，而赤道附近区域也是人眼视觉关注度较高的区域。图9 给出了全景视频测试序列。从图9 可以看出，全景视频图像具有类型多样、分辨率高、视域广等特征，有些视频序列的背景图像是静止的，比如PoleVault、Harbor 等；有些视频序列的背景和前景图像都呈现运动变化，比如DrivingInCity、Landing 等。

图9 全景视频测试序列

5.1 率失真性能分析

本文所提算法以VTM14.0 为基准，分别用QP 值为22、27、32、37 去编码每个测试序列。编码率失真性能评价指标为BD-rate。BD-rate 是评价视频编码算法性能的主要参数之一，表示在相同编码质量下新算法相对于基准的码率节省百分比，负值表示率失真性能提升，正值表示率失真性能降低。表2 为基于带权重的空域映射模型的球域率失真优化（WM-SRDO,weighted mapping model based spherical rate-distortion optimization）算法相较于基准的BD-rate。从表2 可以看出，在8K、6K 和4K 测试序列上，分别使用SPSNR、CPP-PSNR 和WS-PSNR 作为客观质量评价指标，WM-SRDO 算法的BD-rate 总体平均为-2.2%、-2.1%和-2.6%，该算法对所有全景视频序列都是有效的。实验结果表明，该算法在一定程度上能有效改善投影过程中的过采样问题，而且运动较小的视频序列的编码性能整体提升更高，比如GasLamp、PoleVault 等。

表2 WM-SRDO 算法相较于基准的BD-rate

表3 为STD-SRDO 算法相较于基准的BD-rate。从表3 可以看出，以S-PSNR、CPP-PSNR、WS-PSNR为客观质量评价指标，BD-rate 总体平均为-7.4%、-7.4%、-7.9%。STD-SRDO 算法对所有测试序列均有效，特别是在8K 全景视频序列上，亮度分量的平均码率节省超过了12%，色度分量码率节省超过了16%。对单个视频序列而言，序列Train 的亮度分量码率节省高达22.6%，Harbor 的色度分量的码率节省达到30%以上。整体来看，大部分8K 视频序列具有图像稳定、背景静止的特征，而考虑失真时域传播的率失真优化算法对这类视频十分有效。对于运动变化较大的视频序列来说，由于帧间预测技术的使用频率相对降低，帧内编码的使用频率相对增高，因此时域依赖程度也会降低，考虑时域依赖的率失真优化算法的编码性能也会相对较低。这一点在6K 视频序列上体现得尤其明显，6K 视频大都具有运动镜头，图像变化快、运动速度高，因而时域传播链相对较短，提升当前帧的编码质量对后续帧的编码质量的改善影响有限。这一点也可以从编码结果上看出，STD-SRDO算法在6K视频序列上的平均码率节省为1.9%。4K 视频序列的图像相对6K 视频变换缓慢，整体上有3.4%的码率节省，这也比较符合图像的运动特征。

表3 STD-SRDO 算法相较于基准的BD-rate（LDP 配置）

表4 为STD-SRDO 算法在LDB 配置下相较于基准的BD-rate。从表4 可以看出，与LDP 配置下编码结果类似，在SPSNR、CPP-PSNR、WS-PSNR 客观质量评价指标下，STD-SRDO 算法平均码率节省达到7.0%、7.0%、7.6%。同样，在时域相关性较强的视频序列上的编码性能提升比较明显。

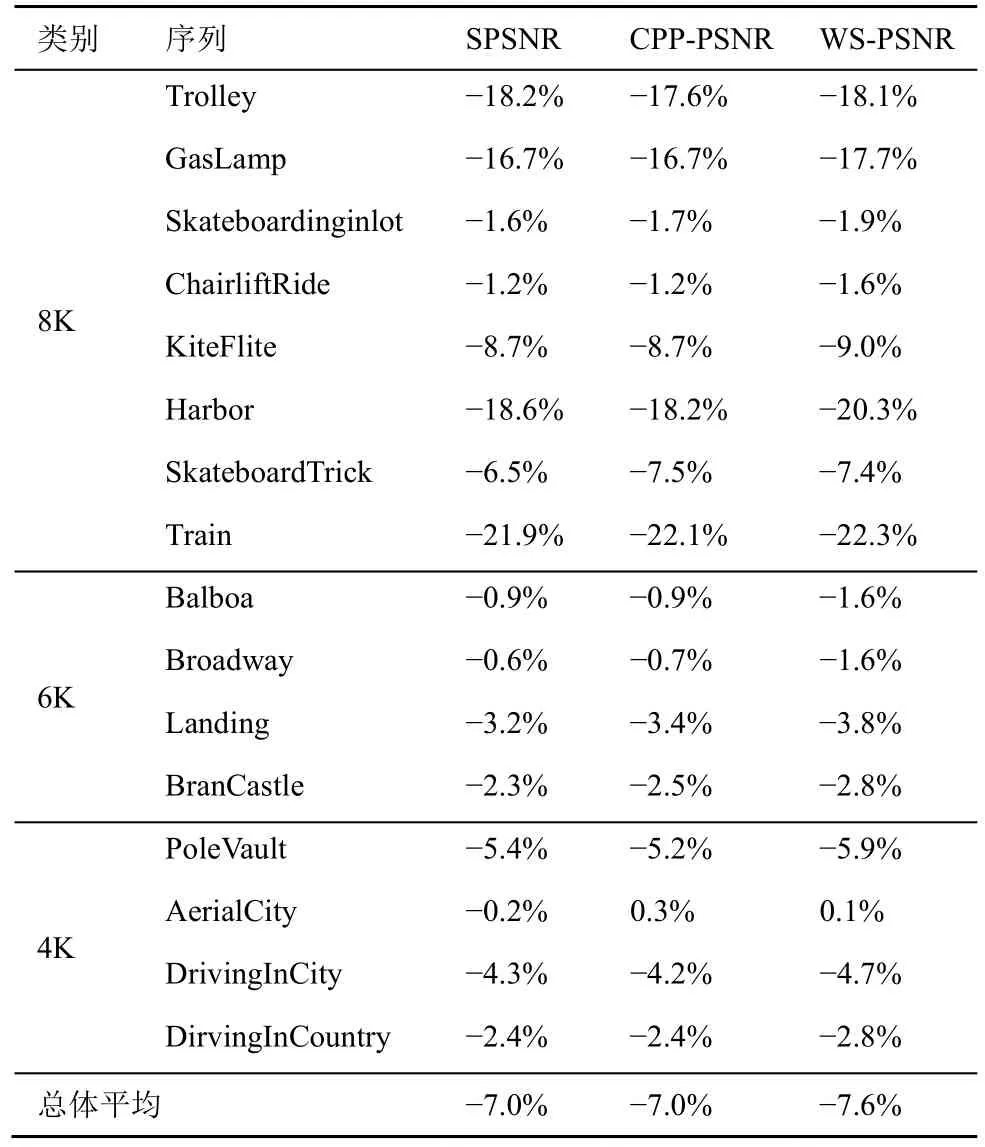
表4 STD-SRDO 算法相较于基准的BD-rate（LDB 配置）

表5 和表6 分别为本文算法与同类算法在LDP和LDB 配置下相较于基准的BD-rate。为简便起见，将SPSNR、CPPPSNR 及WSPSNR 分别缩写为S、CPP 及WS。文献[8]的边界补偿算法有0.5%的码率节省，该算法对运动较大的全景视频比较有效，而运动较小甚至静止图像存在较少的跨边界运动，编码性能提升较少。文献[10]针对CMP 边界进行拓展，以保持图像边界的连续性，性能提升达1.2%。文献[11]在边界补偿的基础上还提出了球域运动模型，平均有2.1%的码率节省。文献[12]提出基于熵平衡的比特分配算法来提升球域率失真性能，整体平均有2.6%的码率节省。文献[13]提出带权重的客观质量评价指标WS-PSNR，并用于调整量化参数，平均有3.2%的码率节省。本文算法在SPSNR 或WSPSNR评价指标下分别有8.1%或8.6%的码率节省，远高于同类算法，特别是在时域依赖强的视频序列上，本文算法效果更加明显，码率节省最高达20%。

表5 本文算法与同类算法在LDP 配置下相较于基准的BD-rate

为了更直观地观察率失真性能对比情况，图10给出了部分测试序列在不同算法下的率失真曲线对比。TD-SRDO 和STD-SRDO 算法分别仅考虑球域失真时域传播以及同时考虑球域失真空域映射和时域传播。从图 10 可以看出，本文算法STD-SRDO 率失真性能更优，特别是在Trolley、Gaslamp、Harbor 等时域依赖性较强的视频序列上效果更加明显。

5.2 编码时间对比

编码时间是衡量算法编码复杂度的重要指标，为了弄清时域依赖算法是否会增加编码复杂度，表7对比了本文算法TD-SRDO 与STD-SRDO 以及基准编码所有测试序列所用时间，比率为算法与基准的编码时间比值。从表7 可以看出，TD-SRDO 算法的编码时间与基准的编码时间几乎持平，观察具体视频序列的编码时间可以看出，运动较大的视频序列的编码时间有所增加，原因为增加了时域传播权重的计算量，比如Skateboardinginlot、ChairliftRide等；而运动较小的视频序列的编码时间有所降低，原因为帧级自适应QP 调整策略使时域依赖强的视频序列的量化参数增大，比如GasLamp、Train 等。STD-SRDO 算法相较于基准的编码时间下降9%；在TD-SRDO 算法基础上，编码时间进一步降低，编码时间下降的主要原因是增加的空域映射模型使高纬度区域的量化参数进一步增加，从而节省编码时间。

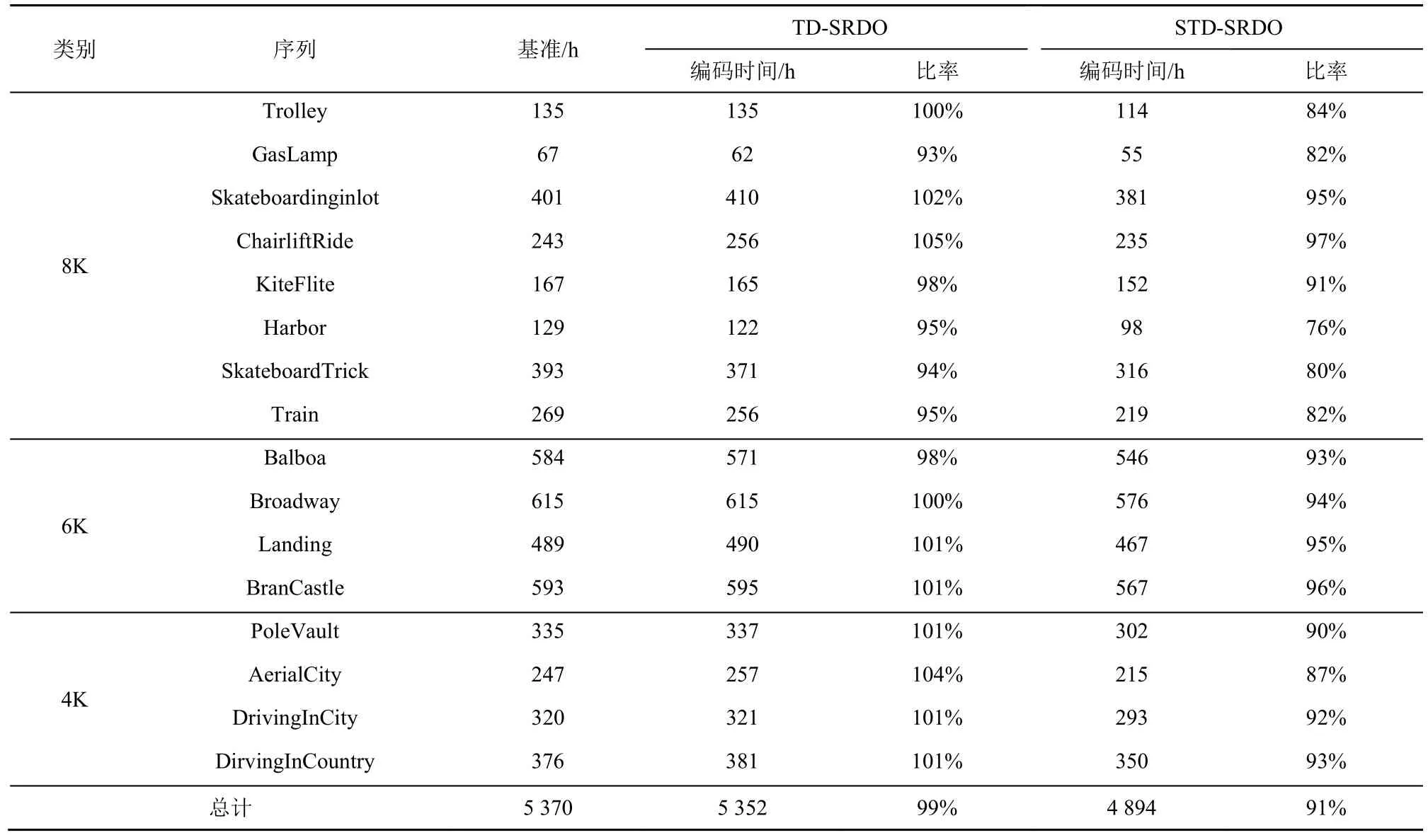
表7 不同算法编码时间对比

6 结束语

本文针对球域失真空-时域依赖的全景视频编码进行了研究。首先，在空域上建立球域失真到压缩失真的映射模型，提升了单帧编码的率失真性能。其次，根据运动补偿预测编码，当前编码单元的失真不仅影响自身的编码性能，还会影响后续帧中与之具有参考关系的编码单元的编码性能，以此建立球域失真时域传播链并量化时域影响权重，再根据球域失真映射权重和时域影响权重来调整拉格朗日乘子和量化参数。实验结果显示，与VTM14.0 基准相比，本文算法实现了7.4%的码率节省和9%的编码时间节省，显著提升了全景视频的编码性能。