用于多载波信号峰均功率比抑制的准互补序列集构造方法研究

2023-11-19李玉博王美悦刘涛陈晓玉

通信学报 2023年10期

李玉博，王美悦，刘涛，陈晓玉

（1.燕山大学信息科学与工程学院，河北秦皇岛 066004；2.河北省信息传输与信号处理重点实验室，河北秦皇岛 066004）

0 引言

相互正交的互补码集（MOCCS,mutually orthogonal complementary code set）由于具有良好的相关特性被广泛用于信道估计[1]和多载波码分多址（MC-CDMA,multicarrier code-division multipleaccess）系统中的干扰消除[2-3]等。然而由理论界限可知，MOCCS 的集合大小不大于每条互补序列中的子序列数目，当集合大小等于子序列数目时，MOCCS 为完全互补码（CCC,complete complementary code），这使互补码在MC-CDMA 系统中海量用户接入[4]的应用受到极大限制。为此，Liu 等[5]提出了准互补序列集（QCSS,quasi-complementary sequence set）的概念，包括低相关区互补序列集（LCZ-CSS,low correlation zone complementary sequence set）和低相关互补序列集（LC-CSS,low correlation complementary sequence set）。LCZ-CSS的相关函数旁瓣幅值在零偏移附近的相关区内很低，当相关区长度等于子序列长度时，LCZ-CSS 被称为LC-CSS。关于序列的相关下界由Welch[6]自1974 年给出后，Liu 等[7-9]在一系列工作中推导出了非周期QCSS 在特殊条件下更加紧密的相关下界，并称达到此下界的QCSS 最优。

到目前为止，针对各种参数的最优QCSS 的构造还不完善。文献[5]利用Singer 差集构造了两类最优和渐进最优的周期QCSSs。通过将文献[5]中的Singer 差集替换为几乎差集，文献[10]提出了一类渐进最优的周期QCSS。文献[11-12]基于有限域上的加法与乘法特征给出了最优和渐进最优的周期QCSSs 的构造方法。然而，前述文献只涉及周期相关特性，文献[13]指出非周期相关特性的QCSS 在实际应用中的重要作用，因此，该文首先提出了渐进最优非周期QCSS，并给出了非周期LC-CSS 的3 种构造，然而，其构造的序列集中互补序列的数目不多且子序列长度受限于素数，尤其是对于二元QCSS，其互补序列数目甚少，不利于其在多用户接入场景下的应用。文献[14]提出了一种具有渐进最优参数非周期二元LCZ-CSS 的构造，具有渐进最优参数非周期二元LC-CSS 可从所提的构造中导出，该文构造的序列集的互补序列数目较多且为二进制序列，因此在实际系统中更容易实现。众所周知，多载波通信系统存在信号峰均功率比（PAPR,peak-to-average power ratio）过高的问题，高PAPR值可能使发射机前端电路饱和，导致发射信号非线性失真，进而降低系统性能。结合互补码集与MC-CDMA 系统的特点，文献[15]通过分析时域扩频MC-CDMA 信号结构，得出时域扩频MC-CDMA系统信号PAPR由用户扩频的CCC所组成二维矩阵的列向量所决定的结论。为解决该问题，文献[15]基于广义布尔函数构造了具有低列向量PAPR 的CCC 集。近年来，文献[16]进一步基于多变量函数构造了具有低列向量PAPR 的CCC 集。相比传统CCC，QCSS 具有序列数目众多的优势，因此在大规模多址接入场景中有巨大的应用潜力。然而目前QCSS 的构造方法并不多，而且已有的构造方法都没有考虑到时域扩频MC-CDMA 信号PAPR 抑制[17-19]的问题，因此在最差情况下系统信号PAPR 达到了最大值，即与子序列数目相等，这在子载波数比较多的系统当中是难以接受的。构造具有低列向量PAPR 的QCSS 一方面可以解决海量用户接入的问题，另一方面可以解决时域扩频多载波系统信号PAPR 过高的问题，这是本文的主要研究动机。

在实际应用中，二元序列直接对应二进制相移键控（BPSK,binary phase shift keying）调制，具有方便实现的优点，因此相比于其他单位圆上的多相复数根序列，二元序列是更加理想的扩频序列。本文基于正交Golay 序列（OGS,orthogonal golay sequence）集，提出了一类渐进最优非周期二元QCSS 的构造。相较于文献[14]，本文提出的构造不仅具有更多数目的准互补序列，且有至多为2 的列向量PAPR。最后，将构造得到的LC-CSS 在准异步QCSS-MC-CDMA 系统中进行误码率（BER,bit error rate）仿真，可以看出，其与文献[14]具有相似的BER 性能，但由于其列向量PAPR 远小于后者，可解决时域多载波信号PAPR 过高的问题。

1 基本概念和定义

定义1令a=(a0,a1,…,aN-1)和b=(b0,b1,…,bN-1)是两条长度为N的二元序列，其非周期互相关函数定义为

当a=b时，,b(τ)为非周期自相关函数，记为(τ)。

定义2定义C={C0,C1,…,CK-1}包含K条互补序列，每条互补序列Ck由M条长度为N的子序列组成，即

最大非周期自相关函数幅值δa和最大非周期互相关函数幅值δc分别为

定义3对于集合C={C0,C1,…,CK-1}，如果其满足式(4)条件，则称序列集C为LCZ-CSS。

其中，0≤k1≠k2≤K-1且0≤τ≤Z-1，或0≤k1=k2≤K-1且0〈τ≤Z-1，0 〈δmax≪MN。序列集C参数表示为(K,M,N,Z,δmax)-LCZ-CSS，其中，K为互补序列数目，M为每条互补序列的子序列数目，N为子序列长度，δmax是长度为Z的低相关区内的最大非周期相关函数幅值。特别地，如果Z=N，则称序列集C为LC-CSS。

为评估QCSS 相关性能的优劣，Liu 等[20]给出了QCSS参数需满足的理论界限，如引理1 所示。

引理1[20]对于(K,M,N,Z,δmax)-LCZ-CSS，δmax满足

Liu等[8]提出了对于非周期LC-CSS更加紧密的相关下界，如引理2 所示。

引理2[8]当K≥3M，M≥2及N≥2时，对于非周期 (K,M,N,δmax)-LC-CSS，δmax满足

为便于分析相关性能，定义最优因子ρ分别为

显然，ρ≥1。当QCSS 的最优因子ρ=1时，称其为最优的；当1〈ρ≤2时，称其为渐进最优的。

定义4记a=(a0,a1,…,aN-1)为一条长度为N的二元序列，将序列a扩展到具有N个子载波的多载波通信系统中，假设基频为0，相邻子载波间的频率间隔为1，则时域多载波信号可以被写为

Liu 等[15]指出，MC-CDMA 系统中的PAPR 控制问题是由互补矩阵的列向量PAPR 决定的，因此，多载波系统中的峰均功率控制问题是降低所有互补码的列向量的最大PAPR。例如，给出一条含有8 个长度为7 的子序列的二元互补序列，并将其写成矩阵的形式

图1 给出了该互补序列中4 条列向量的IAPR曲线。在多载波通信系统中，由式(9)可知，由于多个子载波在某个时刻以同一个方向进行累加时，会产生较大峰值，在最差情况下，所有子载波同时达到最大值，此时PAPR 为子载波数目，如图1 中d0的IAPR 最大值为子序列数目8。当信号峰值进入功率放大器的非线性区域时，会使信号产生畸变，从而产生载波间干扰和带外功率辐射，降低系统性能。因此，对于多载波信号PAPR 抑制的QCSS 构造方法的研究是很有必要的。

图1 4 条列向量的IAPR 曲线

因此，本文工作的目标是构造低列向量PAPR 的QCSS，这将有2 个方面的好处：一方面，系统的PAPR得到抑制；另一方面，互补序列的数目得到扩展。这2 个方面的优势使所构造的QCSS 在海量用户接入的MC-CDMA 系统具有较大的应用潜力。

2 QCSS 的构造

步骤1有限域 F2n，其本原元为α且n≥3 。取一正整数Z使Z≤2n-1。

互补序列C(u,k,v)中的每个元素定义为

定理1经由上述方法构造得到的互补序列集C具有如下性质。

2) 每个互补矩阵的列向量PAPR 上界都为2。

证明详见附录1。

由于LC-CSS 是LCZ-CSS的一个特例，因此可从定理1 直接得出以下推论。

推论1在定理1 的序列集C的构造中设置Z=2n-1，那么由此构造的序列集C是非周期二元(2nU,2n,2n-1,2n)-LC-CSS 。

在上述构造中，显然，映射集π的构造是一个关键因素。文献[14]利用有限域上的本原元构造了一个包含有2n条映射序列的映射集

其中，0≤t≤2n-2，α是GF(2n)的本原元，ϕ是从 F2n到Z2n的一对一映射函数，取 F2n中元素的十进制形式。本文给出一种新的映射集π的构造方法，具体如引理3 所示。

引理3记有限域GF(pn)，p为素数，n为正整数。在GF(p) 上选择一个n次本原多项式f(x)，以f(x) 为m序列的生成多项式，各寄存器的非零状态序列记为G={β0,β1,…,，对G的各项依次加上一个固定状态，并用十进制表示，则可得到pn条长度为pn-1的从的一对一映射序列πu，具体定义式为

证明详见附录2。

引理3 构造了不同于文献[14]的映射集。事实上，映射集π所满足的性质与非重复一次碰撞跳频序列的性质相似，因此可以通过寻求这样的跳频序列来进一步构造许多满足定理 1 的QCSS。

证明详见附录3。

推论3利用引理3 的映射集，根据定理1 构造的 (22n,2n,2n-1,2n)-LC-CSS 可知，引理3 构造的准互补序列集是渐进最优的。

证明详见附录4。

表1 列出了本文和文献[14]在Z=4和3≤n≤10时的二元LCZ-CSS 的参数比较。从表1可以看出，本文相较于文献[14]扩展了互补序列的数目。

本节给出了低列向量PAPR 的渐进最优非周期二元QCSS 的构造方法。首先给出了列向量PAPR上界为2 的QCSS 的一般构造框架，其次将引理3构造的映射集代入构造框架中，进而可以构造渐进最优的QCSS，经此构造得到的QCSS 不仅互补序列数目多且其列向量PAPR 上界为2。文献[21]利用布尔函数构造了过载率最大为4 的二元OGS 集，通过更换不同的OGS 集，进而可以构造QCSS。例如当n=5 时，可以构造4 个满足定理1 的QCSS，大大增加了系统中可容纳的用户数目。文献[21-22]已经构造出大量的OGS 集，本文提出的构造方法的优势是基于多个二元OGS 集可得到多个渐进最优的非周期二元QCSS，其内的每个互补序列都有低列向量PAPR，且其上界为2。

3 QCSS-MC-CDMA 系统中的性能分析

考虑具有子载波为M、码片持续时间为N的上行链路QCSS-MC-CDMA 系统，假设有K个用户，其中第0 个用户为期望用户，即它是在多个用户存在的情况下检测信号的预期用户。系统的收发端结构如图2 所示，其中bk(n) 代表第k个用户的BPSK的信号，假设该系统为准异步系统，考虑均值为0的高斯白噪声信道。

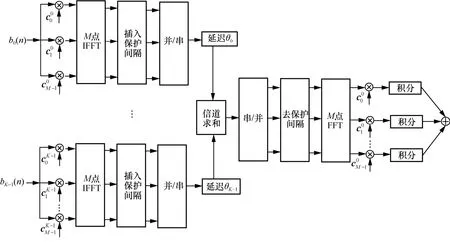
图2 准异步QCSS-MC-CDMA 系统的收发端结构

首先利用为每个用户分配的互补序列对调制信号进行扩频，将得到的扩频矩阵按列进行快速傅里叶逆变换（IFFT,inverse fast Fourier transform）以获得时域样本，然后加入循环前缀以抑制符号间串扰和子载波间干扰，接着经过并串变换得到用户要发送的信号。接收端的接收信号可表示为

其中，N0表示噪声向量。类似地，其他用户的接收信号可以通过在接收端处改变解扩码来获得。

取n=5，Z=31，基于引理3 和文献[21]的OGS 集可构造4 个QCSS，每个序列集的参数为(1024,32,31,32)-LC-CSS，从所构造的QCSS 中选取K=8 个用户进行仿真实验，蒙特卡罗仿真次数为 104。图3 为本文和文献[14]所构造互补序列进行多载波调制后的列向量IAPR 的比较，图4 给出了两者所有列向量PAPR 分布的比较。从图3 和图4可以明显看出，本文互补矩阵的列向量PAPR 最大为2，而文献[14]中互补矩阵的列向量PAPR 最大为子序列的个数32，即本文所构造的序列应用到MCCDMA 系统中信号的IAPR 得到了有效的抑制。图5为本文和文献[14]构造的 QCSS 在准异步QCSS-MC-CDMA 系统中的BER 性能的比较。从图5可以看出，两者具有相似的BER 性能，但是本文所构造的QCSS 具有更低的列向量PAPR 且有更多的互补序列数目。

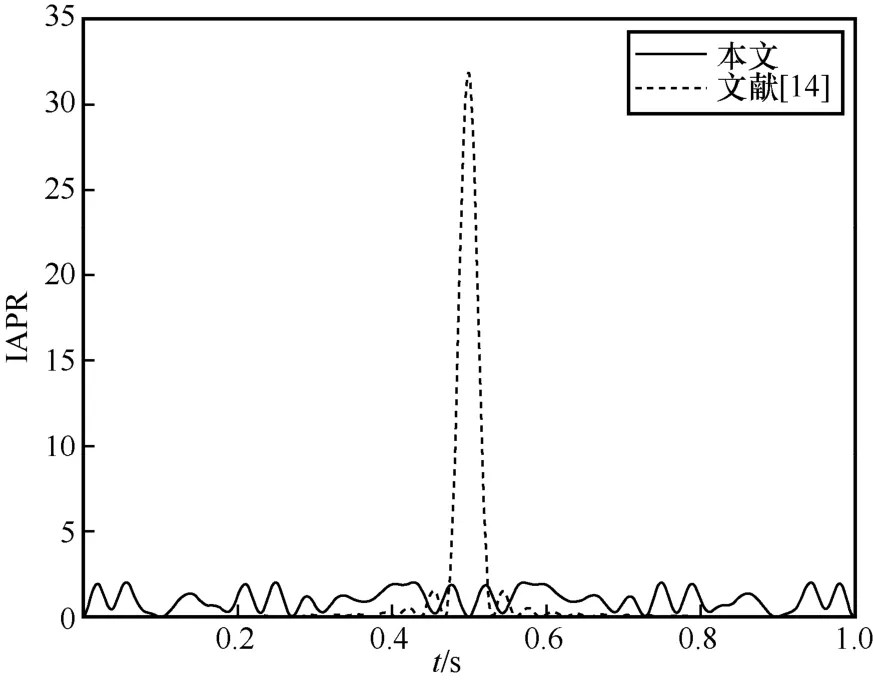
图3 本文和文献[14]所构造互补序列进行多载波调制后的列向量IAPR 的比较

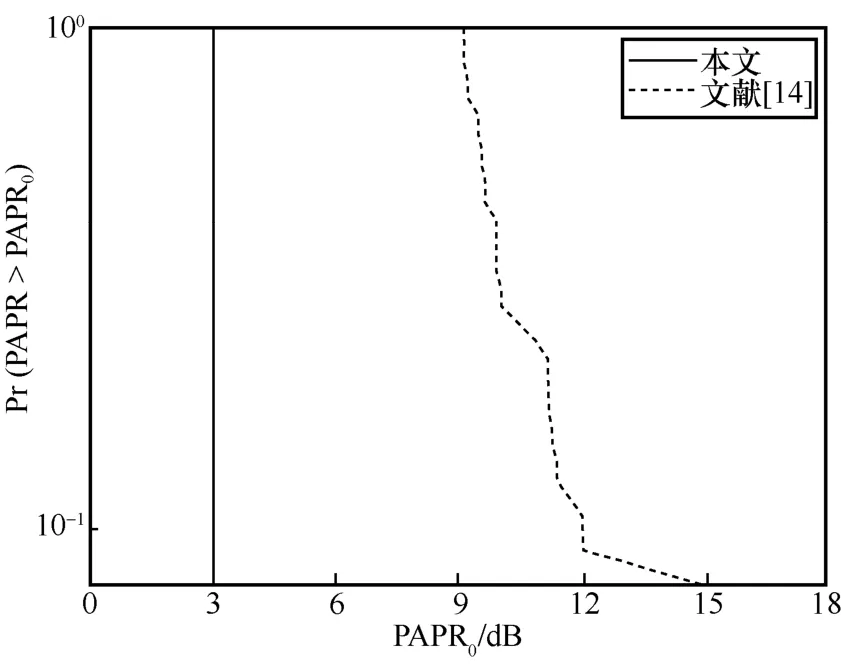
图4 本文和文献[14]所构造互补序列进行多载波调制后的所有列向量PAPR 分布的比较

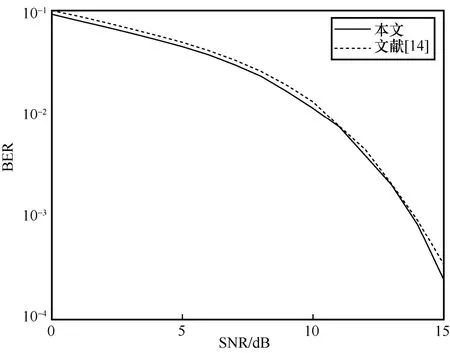
图5 本文和文献[14]构造的QCSS 在准异步QCSS-MC-CDMA 系统中的BER 性能的比较

以上仿真结果很好地验证了前述理论分析的正确性，相较于文献[14]，本文构造的QCSS 不仅抑制了系统PAPR，而且大大扩展了互补序列数目，然而，值得注意的是，本文利用OGS 集作为初始序列集构造QCSS 属于间接构造法，最后得到的序列集的参数依赖于初始序列集的参数，这是本文方法的一个不足之处，研究序列的直接构造法是笔者下一步的研究方向。