基于微分进化算法的无线传感器网络覆盖优化问题研究
2023-11-18坎香,方伟
坎 香 ,方 伟
1.江阴职业技术学院 计算机科学系, 江苏 江阴 214405;2.江南大学 物联网工程学院, 江苏 无锡 214122
无线传感器网络(wireless sensor networks,WSN)涉及传感器技术、无线通信技术、嵌入式技术、分布式信息处理技术等多个学科领域的内容,是当今学术研究的热点领域之一[1-3]。WSN中的传感器节点采用无线连接,以多跳自组织方式形成网络,将感知信息传送至汇聚节点,再由汇聚节点通过卫星或物联网发送至终端的任务管理节点进行统一分析管理。WSN 的覆盖方法是WSN 的一项关键基本技术,该方法的优劣关系到组网成本和网络容错能力,以及整个网络的工作效率。因此,WSN 的覆盖优化方法是国内外专家学者的重点研究方向之一[4-6]。
近年来,群体智能算法由于出色的寻优能力被广泛应用于WSN 的覆盖优化[7-9]。文献[10-11]提出利用遗传算法较强的全局搜索能力和并行搜索能力实现WSN 的覆盖优化,但受局部搜索能力的限制,算法在最优解附近收敛速度慢,从而导致动态节点选择的实时性不高;文献[12]以最大化节点间的距离为适应度函数,将微粒群算法应用于WSN 的覆盖问题,实现以簇头节点为中心向外均匀分布的节点部署形式,但该算法未考虑边界约束问题。
微分进化算法是Rainer Storn 和Kenneth Price在1995年为求解切比雪夫多项式而提出,主要特点是收敛速度快、可调参数少、鲁棒性好、算法简单,其基本思想在于利用当前种群不同个体之间的差异,通过重组得到中间种群,并在子代与父代中选择较优个体来获得新一代种群。作为一种新颖的进化算法,微分进化算法在面对非线性、不可微、多目标、多约束的复杂优化问题时显示出高效的寻优能力,目前已成功应用于摄像机标定、生物信息学、工业生产优化、变电站规划、电力系统调度等领域。
目前微分进化算法在WSN 路由算法上的应用较多,但在WSN 覆盖部署问题上的应用尚少。本文针对微分进化算法在WSN 覆盖问题上的应用特点,尝试完善覆盖模型、改进算法的适应度评价函数和选择机制,以实验论证微分进化算法在WSN覆盖问题上的可行性。
1 无线传感器网络覆盖模型及改进
1.1 基本覆盖模型
设WSN 的监测区域A 为L×W的二维长方形平面,将监测区域A划分为m×n个网格点,并布置N个传感器节点。传感器节点的集合为C={c1,c2,…,cN},其中ci={xi,yi,r}((xi,yi)为节点ci的位置坐标,r为节点ci的传感半径),i=1,2,...,N。
本文采用二元感知模型,将节点的感知范围等效成一个以节点位置为圆心、传感半径r为半径的圆。网格点(x,y)是否被传感器所覆盖,可用式(1)进行判断,即
式中:Pcov(x,y,ci)为感知概率,i=1,2,...,N。
在监测区域A 内m×n个网格点中,只要存在一个网格点(x,y),使得Pcov(x,y,ci) = 1,即认为该网格点(x,y)被传感器节点ci所覆盖。统计监测区域A内被覆盖的总网格点数,再由式(2)计算WSN在监测区域A内的覆盖率,即
式中:f为监测区域A内的覆盖率,D为A内被覆盖的总网格点数。
1.2 覆盖模型的改进
1.2.1 传感器圆心范围的约束处理
在对监测区域A 内的L×W二维平面使用微分进化算法进行变异交叉过程中,可能会出现圆心落在区域外的节点,从而减小了节点的覆盖面积。为此,需要将圆心落至监测区域外的节点通过移动的方式移动至监测区域内,具体操作方式如下:
式中:x、y分别表示监测区域内任一传感器节点的横坐标与纵坐标;L、W分别表示监测区域的长和宽,m。
1.2.2 节点过于聚集的处理
为了提高WSN 的覆盖率,在传感器节点部署过程中,很可能出现传感器节点过于聚集导致节点重叠的情况。为限制各覆盖区域内重叠节点的数量,减少节点的重叠区域,需要根据传感器节点ci的位置,计算周边的重叠节点数O(xi,yi),公式如式(4)所示,即
式中:xj、yj分别表示监测区域A内传感器节点cj的横坐标与纵坐标,j=1,2,...,N。
令M是与监测区域A的面积及传感器节点个数N有关的常数,当O(xi,yi)>M时,节点ci的位置需要重新在覆盖区域内随机生成。
2 基于改进微分进化算法的无线传感器覆盖优化方法
2.1 基本微分进化算法
微分进化算法与遗传算法相似,都含有变异、交叉和选择几个步骤,但相对于遗传算法又具有参数少的优点。
2.1.1 变异
微分进化算法的变异操作是在种群中随机选择两个个体作差分运算,然后将所得向量差加权后,根据一定的规则加到第三个个体(基向量)上。这种变异方式有效利用群体中个体间的分布差异,增强了全局搜索性能。
在微分进化中常用的变异算子有5 种,本文采用DE/rand/1的方式,即在传感器分布时从群体中随机选择2 个个体Xr(t)、Xs(t),以及种群中的最优个体Xbest(t),按照式(5)产生新的个体,即
式中:Xr(t) -Xs(t)为2个个体的向量差;F为缩放因子。
2.1.2 交叉
变异中差分运算是微分进化算法的关键。在变异操作完成后微分进化算法采用均匀交叉的方法产生一些试验向量,以增加种群的多样性。具体地说,在无线传感器网络覆盖中,监测区域是个二维平面,种群中第i个个体的位置坐标Xi=(Xi,1,Xi,2)(Xi,1表示第i个个体的第1 维分量,Xi,2表示第i个个体的第2 维分量);对种群中第i个个体的每个分量Xi,k(k=1,2),随机生成一个0~1之间的实数b,将经过变异操作得到的中间个体Ui(t+ 1)和当前进化个体Xi(t)进行杂交操作,得到候选个体Vi(t+ 1),其中第k维分量的操作如式(6)所示,即
式中:交叉因子R∈[0,1];z是针对第i个个体生成的一个属于[1,2]且均匀分布的随机整数。
这种交叉策略使得Vi,k(t+ 1)至少取到一个Ui,k(t+ 1)的值,即候选个体Vi(t+ 1)至少继承一维中间个体Ui(t+ 1)的分量,以确保每个个体都有交叉,从而更有效地提高种群的多样性,保证个体的进化,防止陷入局部最优。
2.1.3 选择
为了保证算法收敛,基本微分进化算法依照贪婪准则进行选择操作,即将经过变异、交叉后产生新个体的适应度值与父代个体的适应度值作比较,让适应度值好的个体进入下一代。因此,在无线传感器网络覆盖问题中,通常将区域覆盖率f作为微分进化算法的适应度函数。选择操作如式(7)所示,即
式中:f(t)为第t代种群的覆盖率,Ct为第t代种群集合。
通常区域覆盖率越大,种群的覆盖能力越强,就更可能被选入下一代中。
2.2 改进的微分进化算法
为提高微分进化算法应用于WSN 覆盖问题上的收敛速度和寻优能力,本文针对微分进化算法中的选择操作,提出一种改进的选择优化机制,具体流程如图1所示。
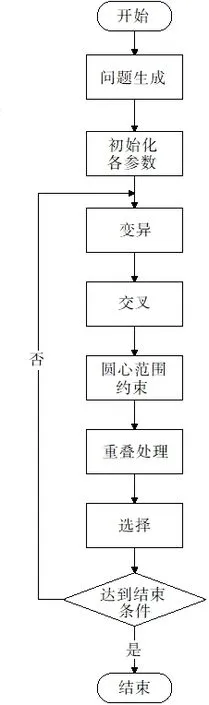
图1 基于改进微分进化算法WSN覆盖优化方法流程图Fig. 1 Flow chart of WSN coverage optimization method based on improved differential evolution algorithm
在微分进化算法中,如何选择最优个体进入下一次迭代是个十分重要的问题。在原微分进化算法中,最优个体的选择采用“优胜劣汰”的淘汰机制,即将变异后的子代个体与原父代个体进行对比,如果比父代更适合生存,那么用子代个体取代父代个体,否则仍采用父代个体。这种算法的特点是收敛速度较慢。
为提高算法的收敛速率,新的群体选择不再采用原来的单个个体的优胜劣汰,而是在原父代Ct与变异后子代群体Ct+1中选出最优的H个个体作为新的种群,并进入下一次迭代过程。在新的选择操作中,采用单个节点的覆盖率(即单个节点的覆盖率对总覆盖率有无提升)对个体进行适应度评价,从而在保证个体变异随机性的同时加大了上一代优异因子留下来的可能性。
按照图1的流程,覆盖优化方法步骤如下:
(1) 明确问题定义域,输入WSN 监测区域、传感器节点以及改进微分进化算法的相关参数。
(2) 初始化H个个体的坐标,即在问题定义域中随机产生H个传感器节点的原始位置,创建初始种群,初始化交叉因子、缩放因子等环境参数。
(3) 按式(5)计算传感器群体中各个节点经过变异操作后的坐标。
(4) 将经过变异后各节点的中间个体坐标按式(6)计算传感器群体中各个节点经过交叉操作后的坐标。
(5) 判断传感器群体中各个节点圆心是否落在监测区域外。针对落在监测区域外的节点,按式(3)对这些节点的坐标进行重新计算,使得这些节点移动至监测区域内,以对其进行圆心范围的约束处理。
(6) 根据传感器群体中每个节点ci的坐标位置,按式(4)计算周边的重叠节点数O(xi,yi);当O(xi,yi)>M时,将节点ci的位置重新在覆盖区域内随机生成。
(7) 对经过上述步骤产生的候选传感器节点群体中的每个节点,采用每个节点的覆盖率对每个节点进行适应度评价;然后从候选传感器节点群体和当前传感器节点群体中选出H个适应度值(节点覆盖率)最大的节点,作为新的传感器群体中的节点。
(8) 判断当前传感器节点群体的覆盖率是否达到预先设定的值或者当前算法的迭代次数是否达到最大迭代次数。若满足,则算法结束,输出最优解即为传感器群体中最优的节点;否则,返回步骤(3),继续进行下一次迭代。
3 仿真实验及分析
假设仿真实验需要覆盖的传感区域为100 m×100 m,种群规模H=40,即有40 个相同配置的无线传感器,每个传感器的传感半径r=12 m,最大迭代次数d=200,缩放因子F=0.7,交叉因子R=0.5。仿真实验在MATLAB 环境下进行,每个实验都随机进行30次,并记录平均覆盖率。
3.1 传感器圆心范围的约束处理对覆盖率的影响
采用基本微分进化算法,比较覆盖优化模型在传感器圆心范围约束处理前后的影响,结果如图2 所示。从图2 可以看出,覆盖优化模型加入范围约束后,随着迭代次数的增加,迭代曲线更加平缓,平均覆盖率从82.67%上升到89.87%。说明圆心范围的约束措施是有效的。

图2 覆盖率收敛曲线Fig. 2 Coverage convergence curve
3.2 重叠节点的处理对覆盖率的影响
采用基本微分进化算法,比较覆盖优化模型在处理重叠节点前后的覆盖能力,结果如图3 所示。由图3 可以看出,覆盖优化模型引入重叠节点的处理之后,随着迭代次数的增加,迭代曲线更加平缓,平均覆盖率从81.79% 上升到89.68%。说明节点的重叠处理措施是有效的。

图3 覆盖率收敛曲线Fig. 3 Coverage convergence curve
3.3 不同微分进化算法对覆盖率的影响
利用改进的覆盖模型,采用基本微分进化算法与改进微分进化算法综合比较算法的平均覆盖率,结果如图4 所示。由图4 的收敛曲线可见,相比基本微分进化算法,随着迭代次数的增加,改进的微分进化算法迭代曲线更加平缓,平均覆盖率从81.40%上升到89.53%。

图4 覆盖率收敛曲线Fig. 4 Coverage convergence curve
3.4 改进覆盖模型及改进微分进化算法对覆盖率的影响
采用改进的覆盖模型和改进的微分进化算法进行仿真,结果如图5 所示。由图5 可见,在优化过程的第一代时,群体的平均覆盖率仅为78.91%;到了第50 代的时候,群体的平均覆盖率达到了88.80%;到了第150 代时,平均覆盖率已达到89.72%。说明随着进化代数的增加,覆盖率逐步上升,即采用的传感器圆心范围约束及重叠节点处理的措施是有效的,能够提高无线传感器的网络覆盖范围。

图5 基于改进微分进化算法及改进覆盖模型的覆盖率收敛曲线Fig. 5 Convergence curve of coverage based on improved differential evolution algorithm and improved coverage model
4 结论
通过将微分进化算法应用于无线传感器分布优化的研究,在对微分进化算法的选择操作进行改进后,发现在同等条件下,与基本微分进化算法相比,改进算法的性能及收敛性能都有了较大提升;改进覆盖优化模型对无线传感器网络的覆盖率也有明显提高。因此,要改善算法的性能,提高网络节点覆盖率,应对覆盖模型进行有效处理,并对基本微分进化算法进行一定的改进。
