基于模糊自抗扰的索网天线容错振动控制研究
2023-11-18王文豪刘磊李阳王辉
王文豪,刘磊,*,李阳,王辉
1.西北工业大学 航天学院,西安 710072 2.陕西省空天飞行器设计重点实验室,西安 710072 3.中国科学院 国家授时中心,西安 710699 4.西安空间无线电技术研究所,西安 710000
1 引言
近年来,索网可展开式天线凭借大口径、高精度、轻质化的优势成为星载天线的主要发展方向[1]。但是索网天线展开后也存在整体结构刚性较低、阻尼较弱的问题[2],由于自身结构特性和工作环境的复杂性,天线会受到冷热交变、温度冲击、卫星变轨等多种内外干扰的影响引起自身的振动,天线型面精度也会受到影响,因此需要对索网天线结构的振动进行控制。
目前国内外的研究中常用的控制策略是采用振动主动控制策略,以作动器作为控制的执行机构达到振动抑制的效果[3]。但是在轨运行的空间索网天线主动调整系统中作动器故障具有不可维修的特点[4],一旦有少部分发生故障,会造成整个控制系统失稳甚至失效。因此,为降低调整机构故障对空间反射面天线带来的风险,研究部分作动器故障下的容错控制方法具有重要的理论意义和现实价值[5]。
过去几十年来国内外学者对于容错控制技术均开展了很多研究工作[6]。Zhao等人建立控制对象的无故障参考模型,在参考模型的基础上,面对作动器可能发生的未知动态故障,设计了一种自适应滑模容错控制器,能够在快速、准确地识别故障的基础上实现控制器的重新配置[7]。但是,该研究对控制对象参考模型要求比较高,因此控制系统的设计难度较大,不适合应用在索网天线这种复杂系统。Xiao等人设计了一种基于输出反馈自适应控制的容错控制策略,实现了在外部干扰导致作动器失效的条件下线性系统的输出反馈补偿跟踪问题[8]。Zhao基于鲁棒控制原理给出一种极点配置方法,保证了冗余作动器控制系统的动态特性,当监控对象发生故障时,通过用亢余作动器来代替故障作动器,保证了控制系统的正常运行[9]。但索网天线作为基频较低、拉索数量可达百根数量级的系统,引入过多作动器可能会导致结构过于复杂,因此不宜采用引入亢余作动器的方案。Liu在主动调整系统参考模型控制律的基础上加入了一种自适应控制律,实现了在不需要故障诊断和检测的条件下,使故障模型渐进跟踪理想模型,达到容错控制的目的[10]。该方法在固面天线的型面结构热控制上得到了应用。综上所述,索网天线振动控制的容错控制方法仍有一定的提升空间。
自抗扰控制(active disturbance rejection control,ADRC)相比于上述控制方法不需要被控对象的精确模型,能有效地处理系统中的非线性、多变量耦合以及不确定性等问题[11],适合应用在天线型面的振动控制当中,但是自抗扰控制器的待调系数较多,系数整定比较困难[12]。通过采用模糊逻辑控制器(fuzzy logic control,FLC)[13],通过模糊控制的自适应能力,不但可以预先预测控制器参数,同时还可以提高控制器对外界因素的抗干扰能力[14]。本文以30m口径索网展开式天线为控制对象,以形状记忆合金丝(shape memory alloy wire,SMA)作为作动器建立动力学模型,考虑作动器损伤故障并建立故障模型,基于模糊控制对自抗扰控制进行改进,给出一种模糊自抗扰容错控制方法,以提高故障后振动控制系统的稳定性、自适应性和故障容错能力,并通过Matlab /Simulink进行了数值仿真,仿真结果验证了所研究容错控制方法的有效性。
2 天线型面的振动动力学模型
2.1 天线的动力学建模
本文所设计并研究的索网天线为30m口径索网展开式天线,由中心环杆、天线反射面索网、调整索、周围肋杆等部分组成,通过与天线型面连接的多组主动拉索对型面的振动进行抑制,其中主动拉索采用SMA作动器控制,索网天线如图1所示。
对于一个大型空间索网来说,很难采用阻尼措施,因此索网结构阻尼小。在模态方程中忽略阻尼的影响,得到的索网天线的无阻尼自由振动方程为:
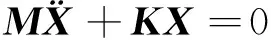
(1)

X=φ×ejωt
(2)
式中:φ为结构自由振动时的振幅向量。将式(2)代入式(1)中,可得:
(K-ω2M)φ=0
(3)
式(3)有非零解的条件为:
|K-ω2M|=0
上式即为结构的特征方程,式中ω为系统的固有频率,求解后可得到天线的m个固有频率,m为结构的自由度,则对于每个固有频率ωi都可以求得方程的特征向量即结构的特征振型φi,将k阶固有频率ωk和k阶固有振型φk代入式(3),并且因为质量矩阵和刚度矩阵具有对称性[15~19],因此可以得到:
因此可以得到索网天线无阻尼自由振动的模态参数矩阵,其中包括其模态质量矩阵M、模态刚度矩阵K、模态振型φk和模态频率ωk,通过进行模态变换,就可以将原有的无阻尼自由振动微分方程变成n个解耦的振动方程。
2.2 作动器的动力学建模
本文中使用SMA作动器作为作动器驱动的主动拉索对天线的型面振动进行控制,SMA具有形变量高、可重复性强、结构简单、可靠性强等优点[20],但由于其自身的材料特性,除了线性动力学外,SMA作动器动力学建模还必须考虑到SMA材料的迟滞动力学特性[21]。设作动器刚度和阻尼分别为kr和cr,将作动器当作一个线性二阶环节处理,则作动器的机械动力学方程可表示为:

(4)
式中:F为SMA加热过程中受到的由温度变化产生的收缩力。由式(4)可以得到SMA作动器机械动力学的传递函数为:
式中:ωα和ξα分别代表作动器的频率和阻尼系数。为准确描述SMA作动器的复杂迟滞效应,本研究使用Duhem模型[22]对SMA的迟滞效应进行建模,将位移作为输出,温度作为输入,采用高斯密度函数作为斜率函数,Duhem模型如下:
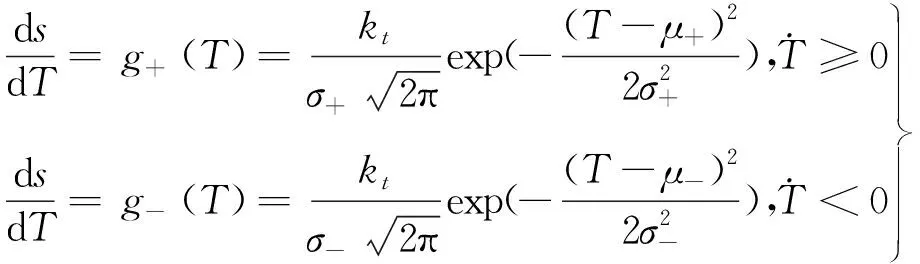
(5)
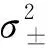
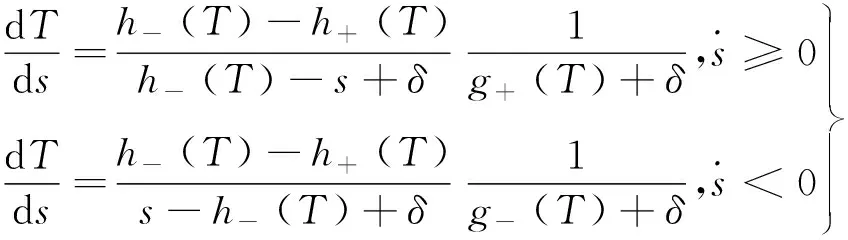
(6)
式中:δ是为使该微分方程有解而选取的常数。式(6)中的g±(T)和h±(T)的定义分别如式(5)和式(7)所示:

(7)
将逆模型连接到控制回路中以消除迟滞效应带来的影响。
2.3 作动器故障模型
本文将作动器设置于与索网节点相连接的主动拉索上,由控制器驱动作动器并输出控制力,以实现闭环控制,作动器数量为12个,其在天线型面上的分布如图2所示。
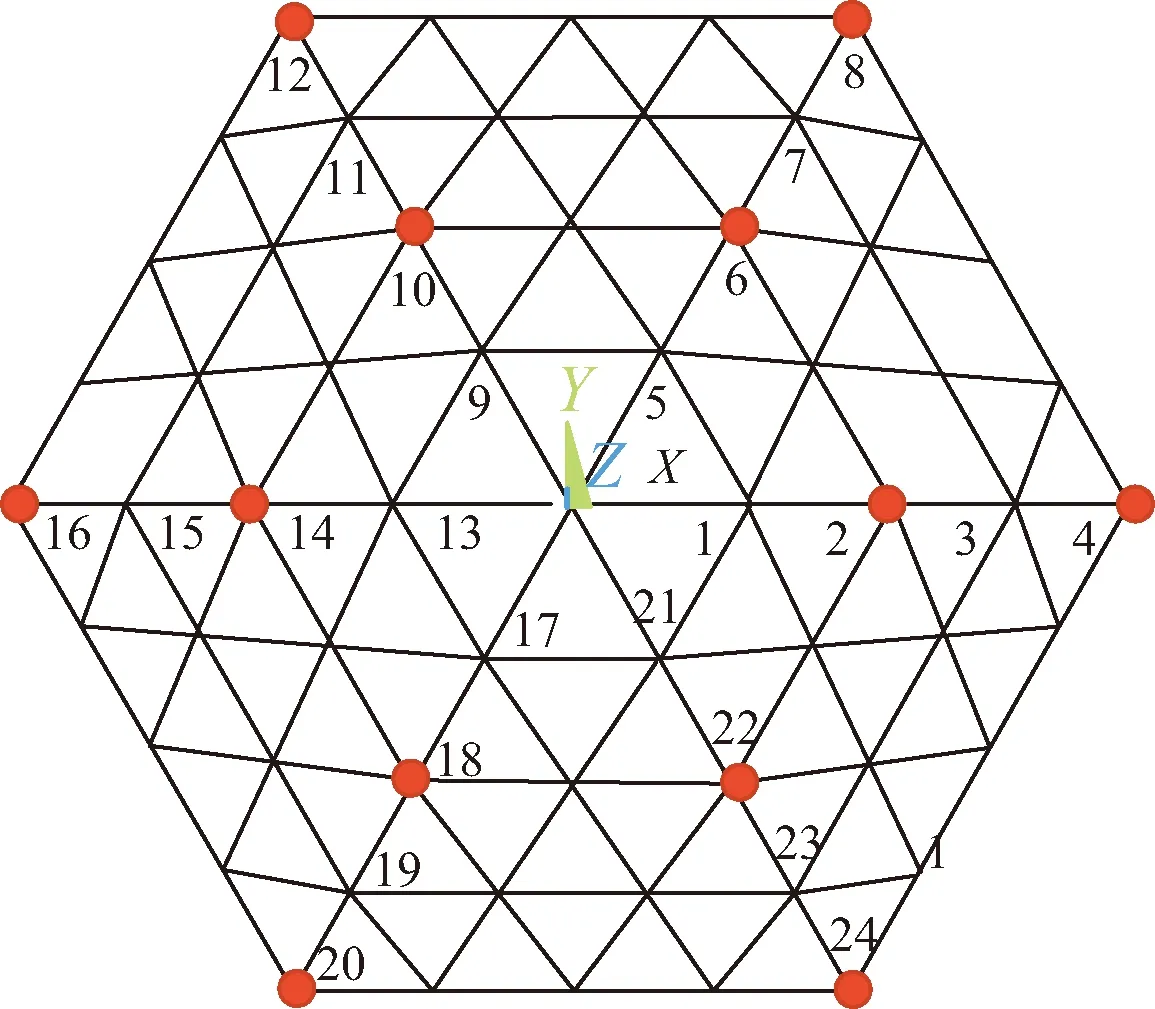
图2 作动器放置位置Fig.2 Position of actuator
考虑到主动调整系统中的作动器会发生故障,将故障对控制系统的影响表现在作动器输出的控制量上,即故障后的作动器只能提供所期望控制量的一部分[23],定义主动调整系统中单个作动器故障控制方程为:
qF(t)=(1-ρ)q(t)
(8)
式中:q(t)表示作动器的预期输出;qF(t)表示故障后作动器的输出;ρ表示故障率,即作动器输出力的折扣率,数值范围在0~1之间。ρ=1时,表明该作动器处于完全失效状态;ρ=0时,说明该作动器处于健康状态;在0~1之间表示处于受损状态。根据式(8),定义作动器系统故障控制方程如式(9):
qF(m)=(I-P)[q1(m),q2(m),…,q12(m)]T
(9)
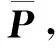
3 模糊自抗扰控制器
针对索网天线振动控制系统作动器发生损伤故障问题,本文根据模糊自抗扰控制技术,提出了一种新的天线振动容错控制方法,其结构如图3所示。
3.1 非线性自抗扰控制器
非线性自抗扰控制器(ADRC)通常由跟踪微分器、扩张状态观测器和非线性反馈控制律三部分组成,其中每个装置根据设计的不同都有好几种可能的选择,因此需要根据控制对象选择合适的控制装置组合。
跟踪微分器模块依据输入信号和被控对象的特性给出合理的过渡过程,不仅能对期望信号进行过渡,而且也能实时地跟踪该信号和其微分信号,实现了对控制目标的快速跟踪,其表达式为:
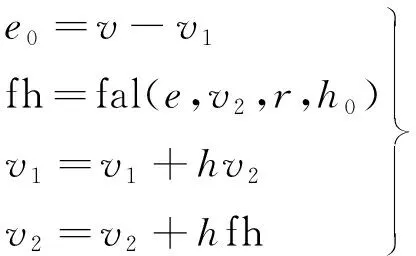
(10)
式中:v为期望输入信号;v1、v2分别为期望值的跟踪信号和微分信号;e0为期望输入信号和实际跟踪信号的差值;r为速度因子,可根据设定输入信号v的函数形式,调整跟踪微分器中参数r的值。参数r主要影响TD的跟踪性能,当增大r时,系统的响应速度增加,跟踪误差减小。h为跟踪因子;h0为滤波因子,通常取接近1的值。
扩张状态观测器是非线性自抗扰控制器设计中最为重要的部分,起到将接收到的不确定性扰动通过补全信息扩张形成系统状态的目的。扩张状态观测器(ESO)系统可表示为:
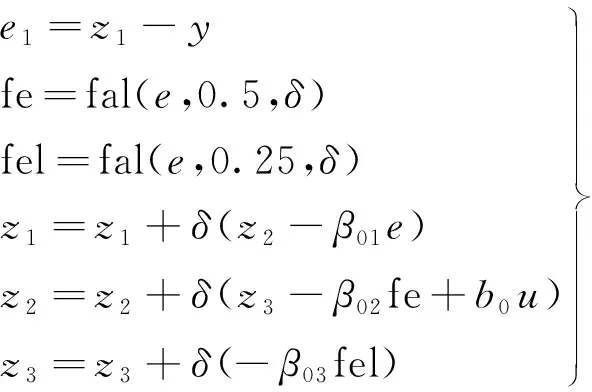
(11)
式中:y为被控对象的输出信号;z1为y的跟踪信号;z2为扰动观测值;z3为状态扩张量;β01,β02和β03为ESO输出误差矫正增益。
非线性控制律主要由误差的比例、微分信号的非线性组合生成控制量,设计非线性状态误差反馈控制律u0(t),实现对系统的控制。该控制器不仅得满足抑制不确定因素,而且输出信号也需良好地跟踪期望值。非线性控制律系统为:

(12)
式中:k0、k1、k2分别为反馈控制中的比例环节、积分环节和微分环节;δ0、δ1、δ2为控制环节增益,对误差反馈控制量u0(t)用扰动估计值z3的补偿来决定最终控制量u。式(10)、式(11)和式(12)中最优控制函数[23]fal的表达式为:
3.2 模糊控制器设计
将模糊控制与自抗扰控制相结合,以改善经典的自抗扰控制。将12个与作动器相连的索网节点作为观测点,以观测点位移e1和位移的微分e2作为输入变量,以非线性控制律中的微分系数Δk1和积分系数Δk2作为输出变量,即该控制器为两输入双输出结构。确定e1的模糊论域为[-3,3],e2的模糊论域为[-3,3],Δk1的模糊论域为[-0.03,0.03],Δk2的模糊论域为[-0.04,0.04]。原理如图4所示。
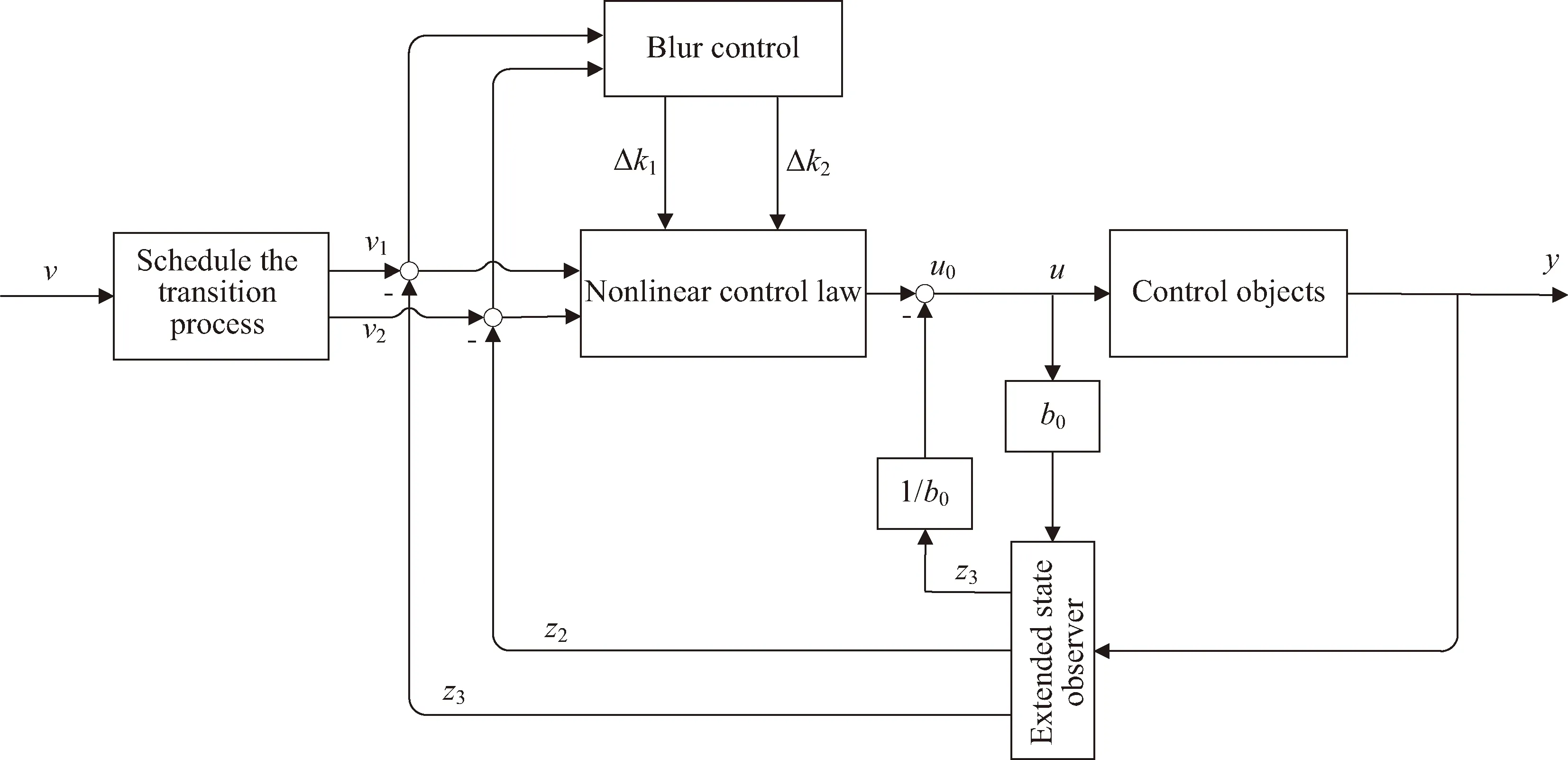
图4 模糊自抗扰原理框图Fig.4 Block diagram of fuzzy active disturbance rejection principle
根据控制精度的要求,将模糊变量划分为7个等级[24],分别为“负大、负中、负小、零、正小、正中、正大”,每个等级对应的模糊子集为{NB,NM,NS,ZO,PS,PM,PB}。为了提高系统的鲁棒性和控制灵敏度,对于最大模糊阶的输入输出变量NB和PB,分别选择正弦隶属函数来提高控制灵敏度;对于其他接近平衡点的阶,采用三角隶属度函数使模糊过程更加平滑,三角形隶属度函数为:
模糊推理采用Mamdani型推理规则[25],根据控制规则给出Δk1,Δk2的变化,模糊规律为:当|e1|较大时,Δk1的值应适当增大,以尽快消除系统误差;当|e1|较小时,选择控制变量要防止系统超调,保证系统稳定;Δk1主要作用是调节响应速度和精度,但要保证Δk1不能过大,过大会使系统超调,导致系统稳定性下降;Δk2的作用是改善系统的动态特性,抑制偏差。
最终的反馈误差控制律的增益系数:
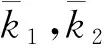
4 仿真分析
为了验证设计容错控制方法的有效性,下面给出作动器无故障和在不同作动器损伤故障参数下,故障容错控制系统性能的仿真分析结果。仿真分析中采用的索网天线口径为30m,取值参考了实验室所用SMA测试数据,SMA作动器机械动力学模型参数分别设定为ωα=20π,ξα=0.3,迟滞模型参数为k=36.0781、μ+=16.6551、μ-=32.3401、σ+=8.9609、σ-=13.4549。天线在轨运行过程中,所受到的扰动往往为复杂的多频扰动信号。为了更好地模拟出天线在太空中的工作环境,在2号节点的位置处施加一个由3个正弦激励和1个随机激励叠加而成的复合激励。3个正弦激励的频率分别为0.9Hz、1.4Hz和1.9Hz,随机激励为一个均值是0、标准差为50的高斯随机信号。以控制器的稳定性、鲁棒性和控制精度为设计基准,在多次调试之后,确定模糊自抗扰控制器的参数设定为r=2,h=0.001,h0=0.05,a0=1,a1=1.5,a2=1.8,δ0=100,δ1=425,δ2=1000,δ=0.2,β01=0.5,β02=0.25,β03=0.75,b0=0.34。对8、10、14、20号这4个位移响应较大的节点处的时域响应进行对比分析,通过12个观测点处的位移响应计算天线的型面精度,如式(13)所示:
(13)
式中:N为观测点的总数;zi为第i个观测点处的位移响应。分2种情况进行仿真比较。
1)作动器无故障,模糊自抗扰控制器正常控制抑制天线型面的振动。4个观测点处的位移幅值变化曲线和复合激励下天线型面精度的变化如图5、图6所示。
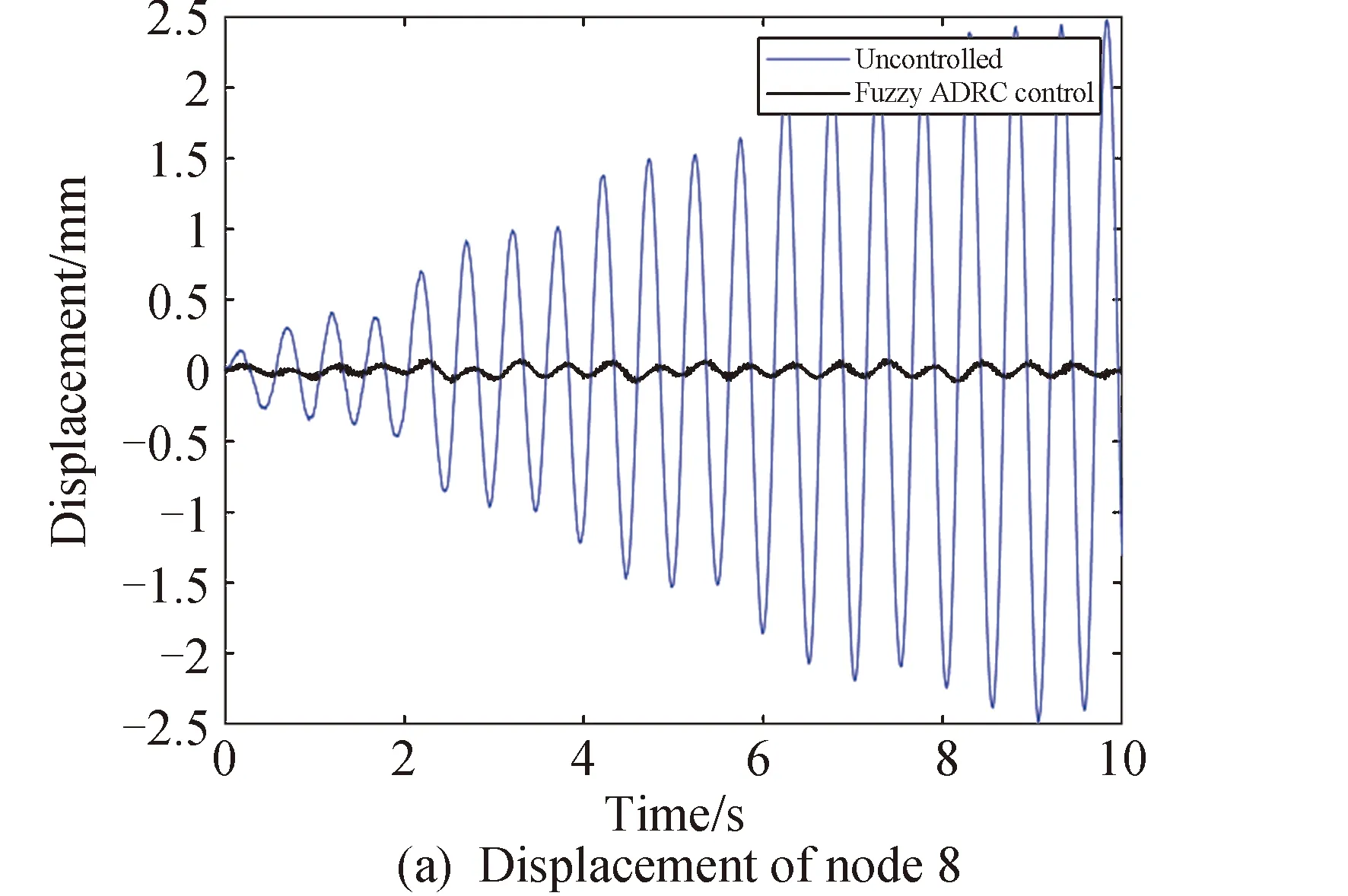
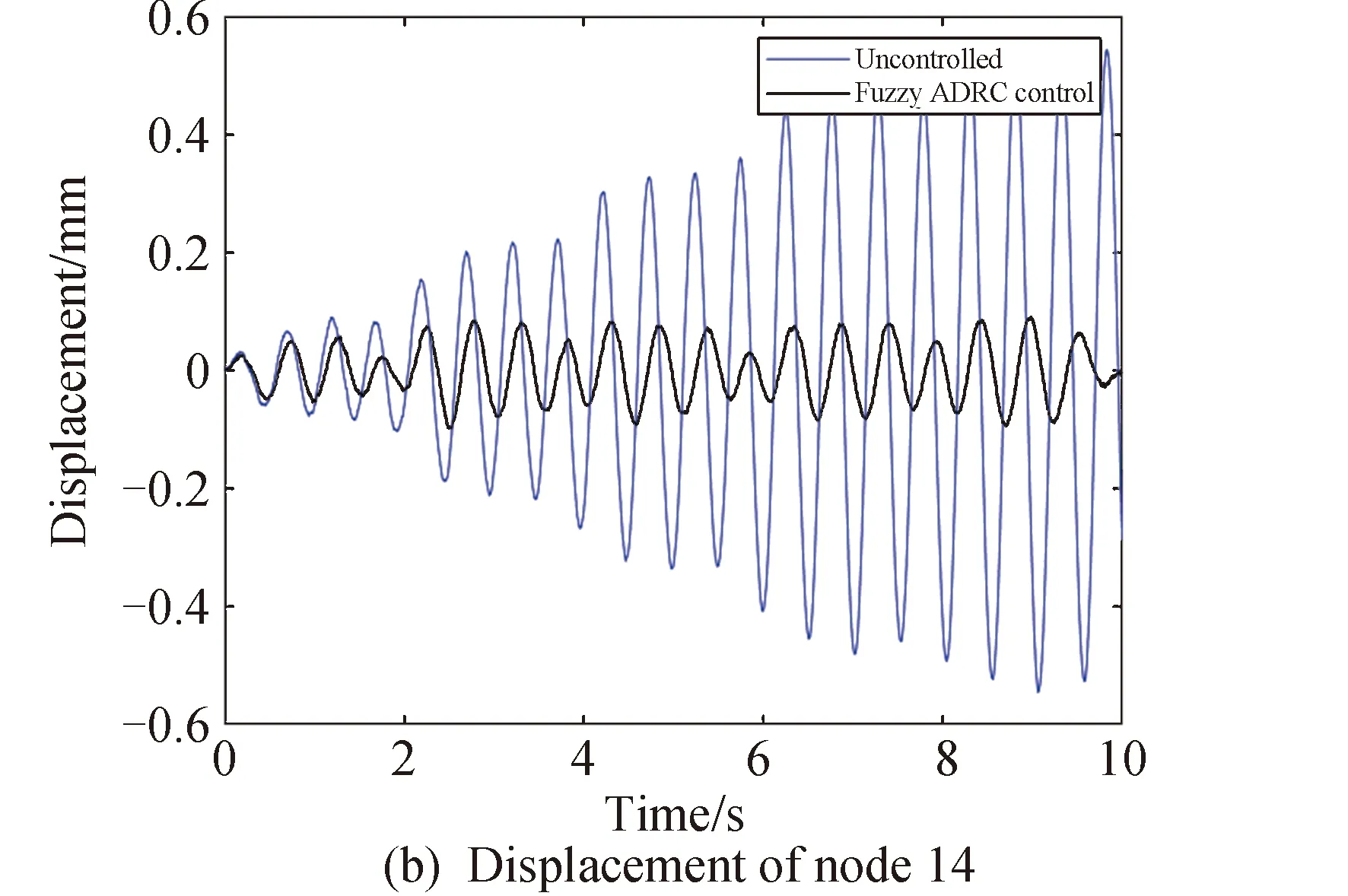
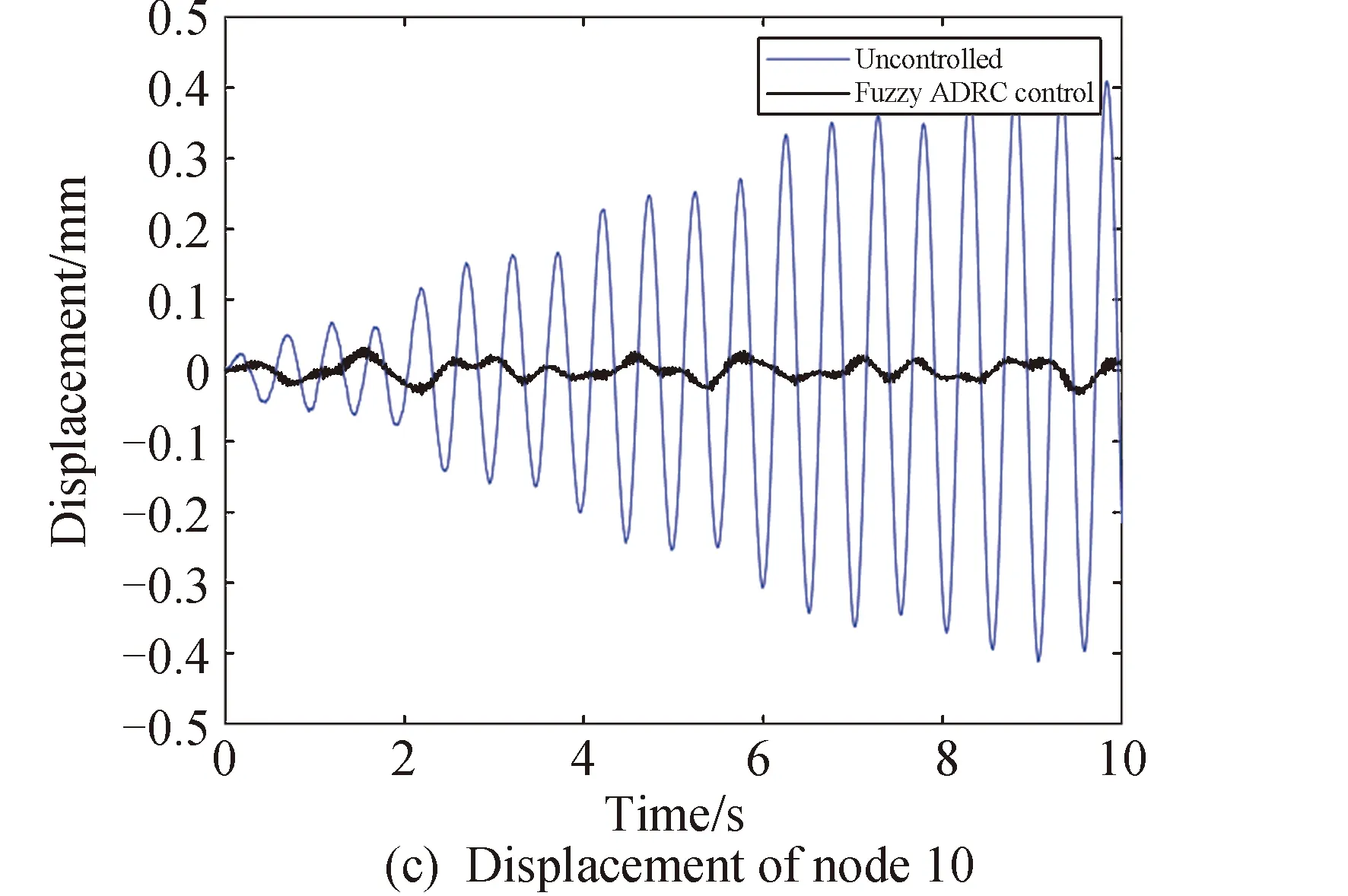

图5 复合激励下天线型面观测点的位移Fig.5 Displacement of observation points on antenna profile under compound excitation
由仿真结果可知:作动器没有发生损伤性故障时,使用模糊自抗扰控制时4个观测点处的位移均方根分别衰减了97.40%、87.68%、93.53%、95.90%。无控状态和模糊自抗扰控制时,型面的位移均方根分别为0.3856mm和0.0218mm。仿真结果说明了无受损情况下模糊自抗扰控制器能够实现对天线型面振动精确的抑制。
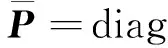

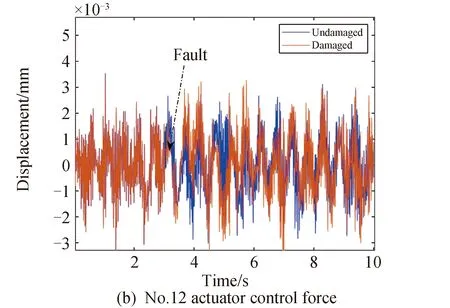

图7 6号、12号、18号作动器控制力Fig.7 No.6,12 and 18 actuator control force
作动器出现较为严重的故障时,控制力波动幅值较大,但最终在较短时间内回到了稳定状态。4个观测点处的位移幅值变化曲线和复合激励下天线型面精度的变化如图8、9所示。
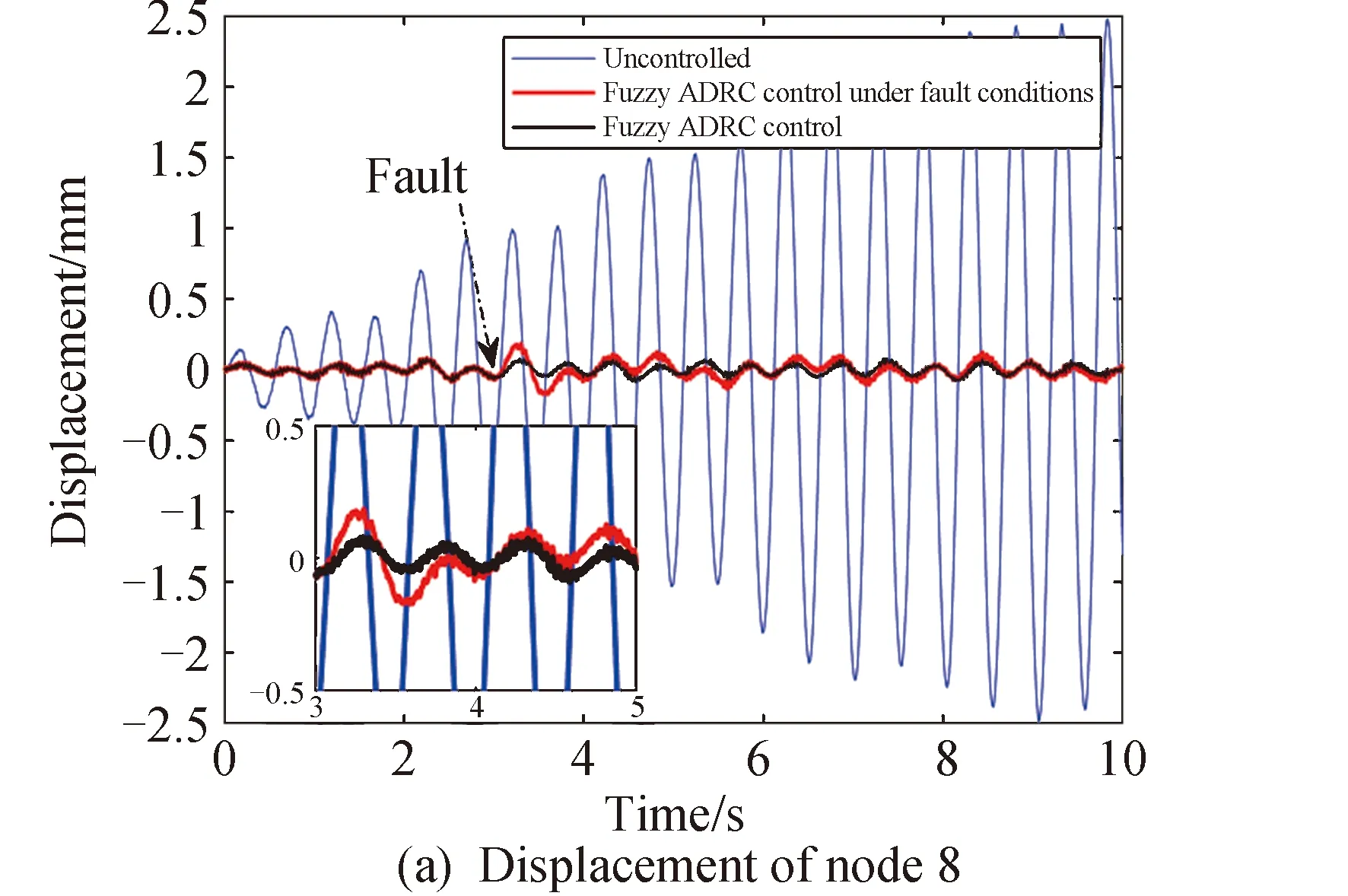
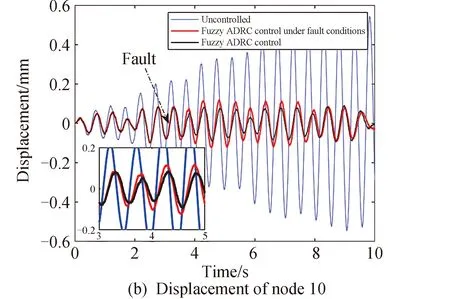
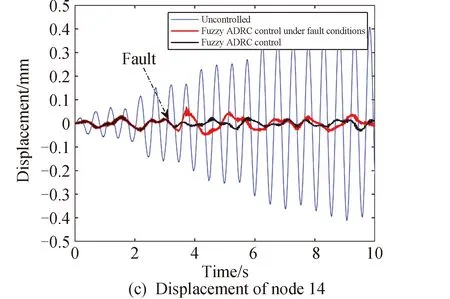

图8 复合激励下天线型面观测点的位移Fig.8 Displacement of observation points on antenna profile under compound excitation

图9 受损条件下复合激励下天线型面精度的变化Fig.9 Variation of antenna surface accuracy under compound excitation under damaged condition
由仿真结果可知:作动器发生损伤性故障之后,4个观测点处的位移均方根相比于无损状态控制效果有所衰减,最终相较于无控状态分别衰减了96.10%、82.43%、88.56%、91.12%。整体的型面精度曲线在故障之后同样发生了振荡,但在控制器的自适应能力调节下又趋近于无损状态下的曲线,型面精度的位移均方根为0.0269mm。
无损状态和作动器受损状态下模糊自抗扰控制器振动控制效果对比如表1所示。
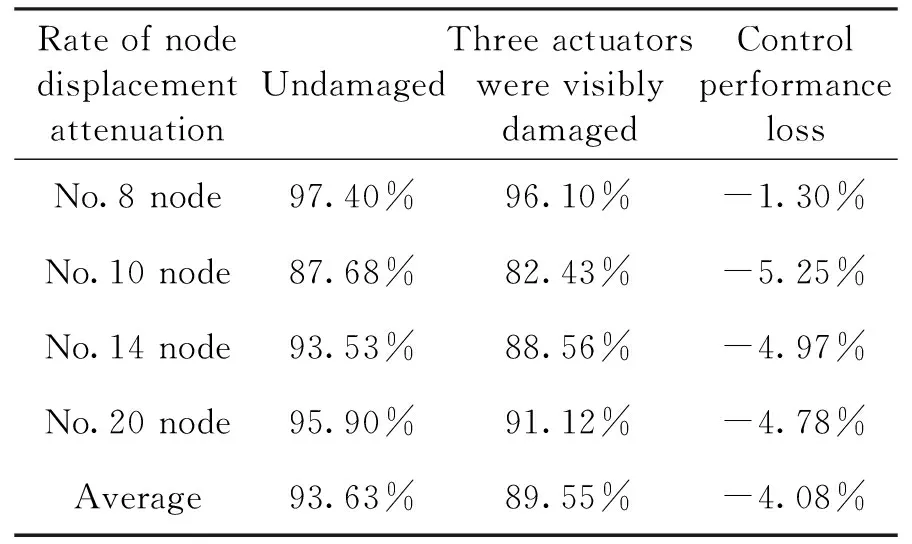
表1 容错控制结果对比Table 1 Comparison of fault-tolerant control results
仿真结果说明作动器受损较为严重的情况下模糊自抗扰控制器控制效果会受到较小影响,但仍能够实现对天线型面振动精确的抑制,具有较强的故障容错能力。
5 结论
本文针对空间索网天线型面振动控制中部分作动器故障问题,为降低作动器故障对空间索网天线型面精度控制带来的风险,给出一种模糊自抗扰容错控制方法。在正弦信号与周期信号叠加而成的复合信号的激励下,通过无损状态和受损状态仿真对比发现:
在作动器正常工作的状态下模糊自抗扰控制时天线型面的振幅相比于无控状态时的振幅减小了超过90%,说明模糊自抗扰控制的方法可以有效抑制天线型面的振动。
在3个作动器较为严重受损的状态下模糊自抗扰控制时天线型面4个观测点的振幅相比于无损状态时的振幅差值平均在4.08%,型面精度的位移均方根增大了0.0051mm,说明模糊自抗扰控制的方法可以有效降低作动器故障带来的影响,实现容错控制。
模糊自抗扰控制方法在空间索网天线型面振动控制中具有一定的应用前景和研究价值。
