基于PSO 算法的反无地基战术激光系统部署方法 *

屈长虹，宋钰，王坤，崔清勇，陈蒋洋

（中国久远高新技术装备有限公司，北京 100094）

0 引言

反无人机作战正在成为未来战场的作战模式之一，反无人机作战系统必将成为防空体系的重要组成部分［1-2］。面对具有成本低、数量多、特征弱等特性的无人机集群，传统防空导弹的拦截成本巨大，而当前快速发展的激光系统是广泛认可的反无人机利器［3］。激光系统就是用高能激光束对远距离目标进行精确射击的定向能系统，它的优点是反应时间短，可拦击突然发现的低空目标，用激光拦击多目标时，能迅速变换射击对象，灵活地对付多个目标。相较于机载平台激光系统而言，地基激光系统具有更高的电源功率、更大的安装空间、更强的制冷能力、更稳定的光束控制，在要地防御场景中可以发挥重要作用［4］。但由于地基激光系统难以在短时间内完成长距离机动，因此地基激光系统对于在战斗开始前的部署位置相较于机载激光系统更为敏感［5］。

本文研究的是地基激光系统的战前部署，属于静态部署问题。首先建立激光系统对匀速直线等高度飞行目标的毁伤模型，在给定若干条无人机可能来袭的方位、飞行高度、飞行速度等条件下，研究如何部署地基激光使无人机突入要地需承受的代价最大。本文使用粒子群算法进行方案寻优，粒子群优化（particle swarm optimization，PSO）算法是一种基于群智能的随机优化算法，相比于其他自然启发算法，PSO 具有更佳的计算时间、收敛相对稳定以及对初值不敏感等一系列优点，已成为求解优化问题的一种经典方法［6-7］。

对于要地防空系统部署问题，文献［8-9］仅考虑了在不同的区域、防线或要地的防空系统的数量部署，未考虑部署位置对部署方案效能的影响，这类研究实质上将部署问题演化为针对不同区域部署系统的数量分配问题。文献［10-11］将防卫要地进行了网格划分离散化处理，使得可部署点有限化。本文的方法可在给定系统数量、规格下，搜索各系统在连续的要地范围内的最优部署位置。

1 问题建模

1.1 相关物理量的定义

设地基激光发射处到目标无人机的距离为L，由于光束衍射、大气抖动和光轴抖动引起的激光光束发散角为γ，则到了传输距离为L处的光束扩散半径为a= tanγ·l≈γ·l，式中的光束发散角γ受光束衍射发散角γy、大气抖动扩散角γt和激光光轴抖动角γd的影响［12］，具体为

式中：λ为激光的波长；D0为出光口径；β为光束质量因子。

设无人机飞行高度为h，激光的光束传输面与无人机下表面存在夹角α，空间几何关系如图1 所示，则有

图1 地基激光系统反无人机作战示意图Fig.1 Anti-UAV battlefield of ground-based laser

出射的光束在三维空间中可视为圆锥形，无人机下表面视为平面，因为存在夹角α，所以在无人机下表面产生的光斑为椭圆形，由几何关系易推知其中短半轴为光束扩散半径为a，长半轴从而得到光斑面积：

设无人机以速度v匀速直线飞行，从地基激光到无人机航线在地面上的投影的距离为y，无人机开始进入激光系统有效射程的时刻二者的空间距离L沿航线的投影为x，由式（3）结合空间关系易推知随着时间t增加，sinα的变化规律为

考虑传输过程中大气对激光能量的吸收，激光通过大气后打到目标上的功率P与激光发射功率P0之 间 的 关 系 为P=P0e-σL，式 中σ为 大 气 衰 减 系数［13］，通常认为根据不同的天气状况，σ的取值范围［14］为0.196～0.078（km-1）。

激光打到目标表面的功率密度定义为功率除以光斑面积［15］：

本文将使用激光系统的防守方记为红方，使用无人机集群的进攻方记为蓝方。设有蓝方无人机沿直线匀速飞行，目标为要地圆心O，地面点P处有一激光系统。作点P到蓝方无人机航线的地面投影的垂线，垂足为点H，如图2 所示。以点H为原点，蓝方无人机来袭方向为x轴正方向，从点H到点P方向为y轴正方向，天顶为z轴正方向建立空间直角坐标系。地基激光系统到蓝方无人机航线的地面距离记为y，亦即地面激光系统的坐标为(0，y，0)。设蓝方无人机在t1时刻从坐标(x1，0，h)处开始受到有效伤害（即功率密度达到阈值），沿直线等高度飞行至t2时刻到达(x2，0，h)处突入要地或功率密度低于阈值，下面分析这一过程中蓝方无人机承受的总激光伤害。

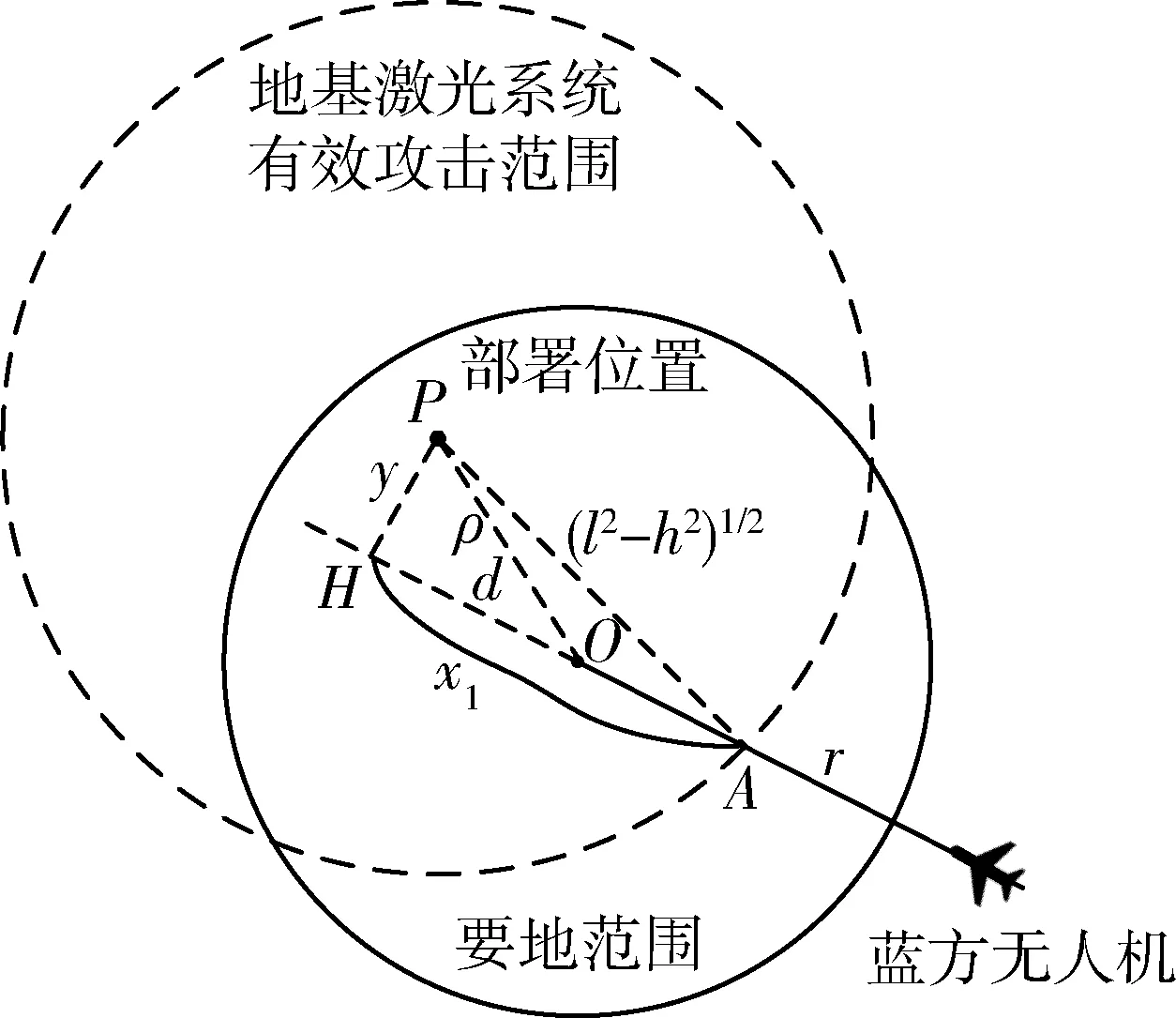
图2 场景及部分物理量Fig.2 Scenario and some physical quantities

激光对目标造成的伤害定义为功率密度乘以作用时间，当功率密度小于毁伤阈值时，激光对目标不造成伤害，当功率密度大于等于毁伤阈值时可以造成伤害，即

式中：B(t)为功率密度随时间变化的函数；1{t：B(t)≥B0}是集合{t：B(t) ≥B0}的指示函数，即当t∈{t：B(t) ≥B0}时函数值为1，当t∉{t：B(t) ≥B0}时函数值为0；t1与t2为起止时刻。由于假定蓝方无人机沿直线向 要 地 圆 心 飞 行，故 蓝 方 无 人 机 从(x1，0，h) 至(0，0，h)一段激光系统到蓝方无人机的距离L单调减小，且sinα因此单调增大，从而功率密度B(t)单调增大；又由对称性易知x2≥-x1恒成立，综上所述，在该过程中功率密度B(t)始终大于等于阈值，可将被积函数中的1{t：B(t)≥B0}省略。

1.2 单台激光系统对单一方向无人机（群）的伤害建模

蓝方无人机沿直线等高匀速飞行时，设速度为v，起始时刻坐标为(x1，0，h)。则t时刻坐标为(x1-vt，0，h)，此时激光系统到蓝方无人机距离的平方为L(t)2= (x1-vt)2+y2+h2，相应的功率密度为

从 坐 标(x1，0，h) 处 沿 直 线 等 高 度 飞 行 至(x2，0，h)处的时刻为于是激光系统对成功突防前的蓝方无人机造成的总伤害为

由于被积函数提取常系数后形如指数函数除以整多项式函数，因此D无法用初等形式表示，为解决此问题，考虑将衰减因子e-σL(t)替换为与之相近的函数。观察易知将形如的函数作为衰减因子与e-σL(t)具有相近的性质：当L= 0 时两者皆等于1；当L→+∞时两者皆趋于0 且在趋近过程中恒大于0。由于两种衰减因子的函数结构不同，两种大气衰减系数σ与c的单位也不同，σ的单位为km-1，与距离L(t)相乘后得到单位为1 的衰减因子；c的单位为km，与距离L(t)相加并相除后得到单位为1 的衰减因子。本文中σ= 0.078/ km，调整参数c的值，当c= 11.2 km 时，两者在0 ≤L≤5 km 范围内有较好的近似，最大绝对误差不超过2%，图3 画 出 了 两 者 在 相 应 参 数 下L在0～5 km 的图像。

图3 两种衰减因子对比Fig.3 Comparison of two attenuation factors

替换衰减因子后，对蓝方无人机造成的总伤害近似为

将式（10）右边的定积分推导成显式形式的过程较繁琐，需经历数次换元及有理函数分离，本文略去推导过程，只保留推导结果：

应当指出，原则上可以直接使用式（9）结合各种积分近似算法（如矩形法、抛物线法等）求值，但需要将积分区间细分、每个区间上函数拟合、求和，必将比使用推导成显示形式直接代入求值的式（10）～（14）消耗更多的计算时间和内存空间。

设定红方要地为圆形，半径为r，红方地基激光可部署范围是要地的同心圆，半径为R，R＞r。以要地圆心为原点，东方为极轴正方向建立极坐标系，于是地基激光系统部署位置可用极坐标(ρ，θ)表示，式中ρ≤R，θ∈[0，2π)。蓝方无人机沿直线向要地圆心突防，来袭方向可用角度α 表示，α∈[0，2π)。

计算D(P0，γ，c，v，h，y，x1，x2)所需的参数中，前5 个是由场景直接设定的固有参数，y是α，ρ，θ的函数，x1与x2是前5 个参数以及α，ρ，θ的函数，下面推导这3 个函数。

首先需要确定地基激光方位与蓝方无人机来袭方位的夹角β∈[0，π]。显然β等于α方位绕逆时针旋转后与θ方位重合的弧度（或者θ方位绕逆时针旋转后与α方位重合的弧度，取其中位于区间[0，π]的那一个值），因为α，θ∈[0，2π)，故当逆时针旋转不穿越极轴时，只需取β=|α-θ|，而当逆时针旋转穿越极轴时，如图4 所示，则需取β= 2π -|α-θ|，逆时针旋转穿越极轴的等价条件是|α-θ| ≥π。综上所述，β的计算公式为

图4 夹角β 的定义示意图Fig.4 Definition of β

有了β的定义后易得

激光系统到航线的空间距离为

记O点 正 上 空h高 处 的 点 为O′。定 义d=ρ·cosβ，当蓝方无人机的飞行轨迹先经过H后经过O′时，亦即；当蓝方无人机的飞行轨迹先经过O′后经过H时，亦即，d＜0，d的绝对值的物理含义为O′到H的距离。

当无人机航线中至少存在一点可使功率密度达到阈值时，x1可定义为功率密度开始达到阈值B0的点到激光系统与航线的垂足点H的距离，此时有

式中：L=直接求解x1 的显示表达式需求解四次代数方程，非常困难，但显然，x1≥0 的取值对B有单调减小的关系，因此必定有唯一的x1的取值使得B=B0，可采用简单的二分法求解任意精度的近似解；当无人机航线中不存在可使功率密度达到阈值的点时，可定义x1= 0。

计算x2需要根据各参数的不同取值造成的不同情形分别处理。情形1：若蓝方无人机在进入激光有效射程之前已突入要地边缘，如前文图2 所示，则应令x2=x1；情形2：若蓝方无人机到达要地边缘时没有脱离激光系统的有效射程，则x2=r-d；情形3：若蓝方无人机到达要地边缘时正处于激光有效射程边缘或者已经从激光的有效射程脱离，则x2= -x1。当蓝方无人机航线有一段进入激光最大射程内时，情形1 等价于

情形2 等价于

情形3 等价于

当蓝方无人机航线不进入激光最大射程时，有x1= 0，且应有x2= 0，此时x1+d＜r与d-x1≥r至少 有 一 个 成 立 ，两 种 情 况 下 都 会 令x2=x1= -x1= 0。解不等式组（19），（21）可得x1＜0，这与定义的x1的非负性不符，因此第1 种情况与第3 种情况的判据之间没有重叠。因此上述3 种情况及其判据已正确划分了所有可能的情形。综上可得：

将式（15）～（22）代入式（11）～（14），即可得到沿航线j飞行的蓝方无人机（群）突入要地前承受来自激光系统i的伤害Dij=D(P0i，γi，c，vj，hj，yij，x1ij，x2ij)，式中参数带有下标i（或j）表示该参数由激光系统i（或航线j上的无人机）决定。

1.3 适应度函数设计

对激光系统的下标求和可得航线j上蓝方无人机（群）突入要地前承受的总伤害：

将所有需考虑的m条航线的承受伤害依次排成 一 列 构 成 列 向 量D(X) = (D1，D2，…，Dm)T，构 造权重对角阵可代表蓝方沿第j条航线来袭的概率或红方需保护对象沿该方向的分布比例等。列向量WD(X)反映了引入权重的影响后部署方案X对各航线蓝方无人机的防御能力，为使得部署方案面对各个可能的蓝方无人机来袭方向都有一定的防御能力，取对最薄弱的方向的防御能力值作为该方案的适应度函数，即

部 署 方 案 可 表 示 为 2n维 向 量X=(x1，x2，…，x2n)，式中：x2i-1，x2i分别表示一台激光系统的部署极角、半径；n为激光系统数。粒子群算法的目标即是要在给定了环境参数、诸激光系统参数和诸蓝方无人机航线参数等参数后，搜索一种最优方案X，使得f(X)最大化：

2 粒子群算法

粒子群中的每个粒子的状态由2 个向量描述：位 置 向 量Xi= (xi1，xi2，…，xiN)，速 度 向 量vi=(vi1，vi2，…，viN)，式中：i为粒子的编号；N为搜索空间维数。每个粒子的当前速度方向vi、自身历史最优位置方向Li= (li1，li2，…，liN)和当前全局最优位置方向Lg= (lg1，lg2，…，lgN)分别对应着粒子的“个体惯性”、“个体认知”和种群的“社会经验”，该粒子的下一步搜索方向是对这3 项信息的折中，对于一个有M个粒子，搜索空间维数为N的粒子群，这种折中用公式表示为

式中：i= 1，2，…，M；j= 1，2，…，N；k为当前迭代步数；xij∈[xmin，xmax]与vij∈[vmin，vmax]分别为粒子i的位置向量第j分量与速度向量第j分量；wk为第k步的惯性权重；η1与η2分别为认识系数与社会系数，统称为学习因子；r1j与r2j为两个独立且服从[0，1]上均匀分布的随机数。一方面，η1与η2代表了粒子向个体历史最优和种群当前最优移动趋势之间的折中，另一方面，wk代表了局部搜索与全局搜索之间的折中。一般来说，当迭代步数k较小时wk较大，以便粒子容易到达未搜索过的区域，算法在这一阶段的全局搜索能力较强；当迭代步数k较大时wk较小，粒子的速度变小，基本只在当前解附近较小区域搜索，算法在这一阶段的局部搜索能力较强。

将部署方案X= (x1，x2，…，x2n)编码为粒子运动空间中的一点，从而一个粒子就代表了一种部署方案。粒子空间中同样的一点在不同的蓝方来袭场景下的适应度值将不同。设定完场景参数再运行算法，粒子群将在粒子空间中寻优。本文所使用的PSO 算法步骤如下：

步骤1：各参数初始化。包括红方要地半径、可部署范围，各台激光系统的功率、波长、光束质量等参数；蓝方各航线的方位、高度、蓝方无人机速度、毁伤阈值，权重；粒子群算法的粒子数、最大迭代次数、学习因子、惯性权重上下限。并随机赋给各粒子初始位置与速度。

步骤2：计算各粒子适应度。将每个粒子i的位置Xi代入适应度函数f，记录粒子i的个体极值位置Li与全局极值位置Lg。

步骤3：判断是否已达到最大迭代次数。若达到，则转向步骤5；否则转向步骤4。

步骤4：按式（26），（27）更新粒子状态，按线性递减更新惯性权重，转回步骤2。

步骤5：输出全局最优位置Lg作为部署方案。

3 仿真校验

为简化分析讨论，将所有激光系统主要性能参数、不同航线无人机飞行参数设为相同。常见的高能激光波长为1 064 nm。光束衍射发散角γy由式（2）计算得出，参照文献［12］中的设定，将光轴抖动角γd设定为，大气抖动扩散角γt取为8 µrad。具体如表1 所示。

表1 参数设定Table 1 Parameter setting

将所有激光系统部署在要地圆心或将所有激光系统完全随机地部署是2 种简单自然的方案，因此使用圆心式部署方案和完全随机部署方案作为参照，将粒子群算法给出的部署方案的适应度值与相同数量的激光系统圆心式部署方案以及完全随机部署方案的适应度值比较。

使用Matlab 软件编写算法的实现程序，主要参数设定如表1 所示。粒子群算法的主要参数为：种群包含粒子数100，最大迭代数800，惯性权重由0.8递减至0.01，认知系数η1= 1.2，社会系数η2= 2.2。在3 种场景下使用粒子群算法得出部署方案。

场景1：红方的要地圆心记为坐标原点，设置蓝方只可能沿0°方向来袭；红方可部署范围为半径1 200 m 的与要地同心圆，可用激光系统数为3 台。部署结果如图5，6 所示。该场景下，粒子群优化部署给出的方案是将3 台激光系统沿来袭方向部署且尽可能前出，以使开火距离尽可能短，符合基本作战经验。

图5 场景1 部署方案Fig.5 Deployment scheme of scenario 1

图6 场景1 收敛进程Fig.6 Convergence process of scenario 1

场 景2：设 置 蓝 方 可 能 沿0°，60°，120°，180°，240°，320°方向以相等概率来袭；红方可部署范围为半径1 200 m 的与要地同心圆，可用激光系统数为6台。部署结果如图7，8 所示。该场景下，需考虑的来袭方向与可用系统数量相等，部署方案近似为每台激光系统防守一个方向，但并未如同场景1 一样尽量前出，这是由于当前参数的激光系统在当前参数的大气环境下达到毁伤阈值的开火距离约为2 050 m，足够在一条航线下方的位置攻击到相邻的航线上的蓝方无人机，算法需要在前出以增强当前方向的防御与靠近圆心以支援相邻两航线的防御之间寻找折中。

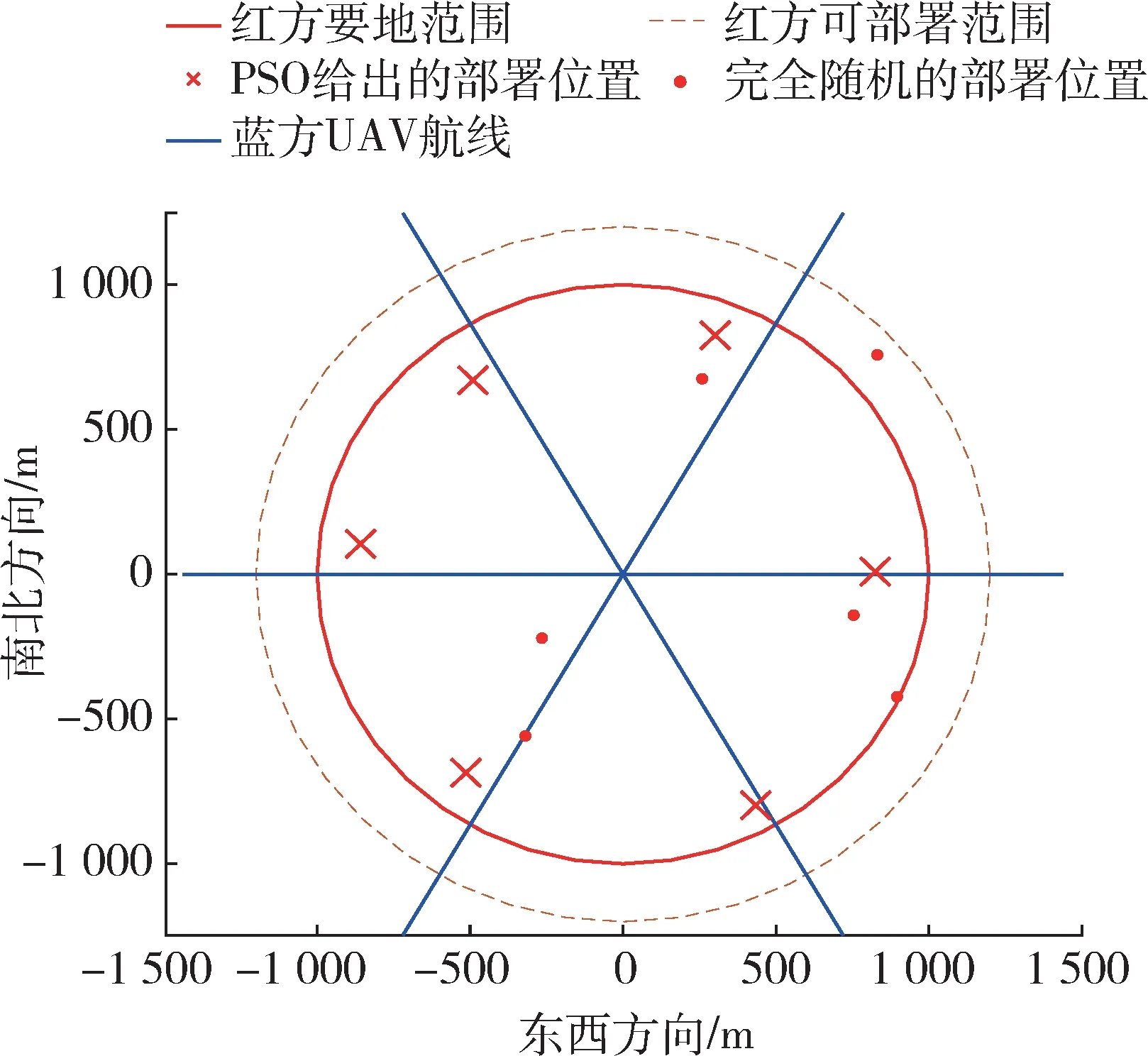
图7 场景2 部署方案Fig.7 Deployment scheme of scenario 2

图8 场景2 收敛进程Fig.8 Convergence process of scenario 2

场 景3：设 置 蓝 方 可 能 沿0°，60°，240°，320°方向来袭，其中0°，320°方向来袭概率分别都为1/3，60°，240°方向来袭概率分别都为1/6；红方可部署范围 为（-1 000，-500），（500，-500），（500，1 000），（-1 000，1 000）4 点围成的正方形，可用激光系统数为6 台。部署结果如图9，10 所示。该场景下，由于0°，320°方向权重是60°，240°方向的2 倍，且可部署范围的左上半部分显然是不利的部署区，因此部署的6 台激光系统都与2 条重要航线靠近且尽可能前出，部署方位在可部署范围内寻找对另外2 条次要航线防御能力的折中。

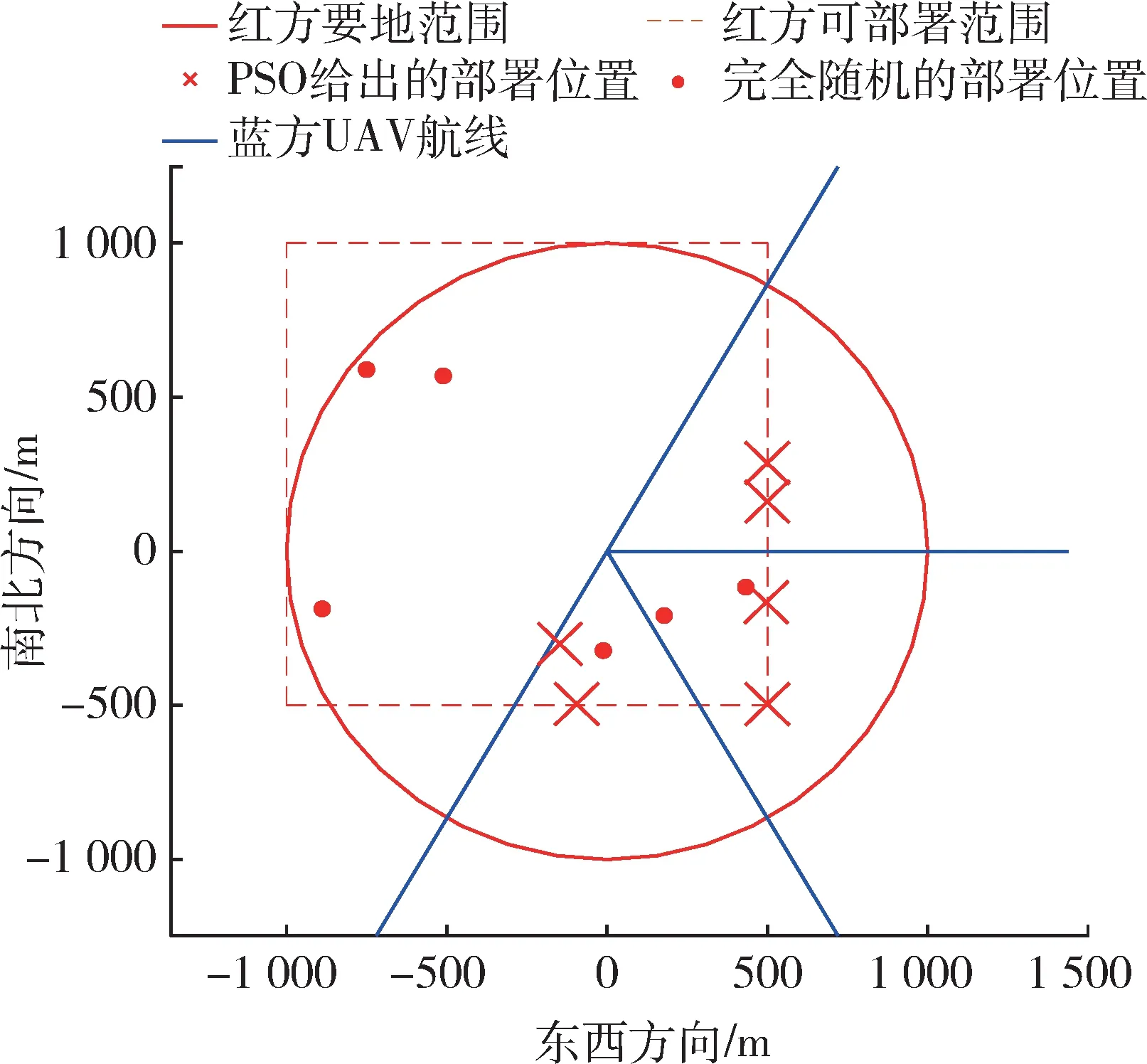
图9 场景3 部署方案Fig.9 Deployment scheme of scenario 3

图10 场景3 收敛进程Fig.10 Convergence process of scenario 3

3 种场景下各方案适应度值如表2 所示，为了直观地显示结果，按如下方式将适应度值归一化：以各场景中圆心式部署方案的适应度值为标准，其他部署方案的适应度值除以圆心式部署方案的适应度值，从而显示出各方案的相对比例关系，表中括号内数据为原始适应度值，括号前数据为归一化后的适应度值。

表2 不同方案适应度结果Table 2 Fitness values of different schemes

由运行结果可以看出，在3 种场景下采用粒子群优化部署都优于圆心式部署和完全随机部署。且粒子群算法具有良好的收敛性，一般在迭代500次左右已基本收敛，使用CPU 主频3.59 GHz，内存16 GB 的台式计算机可在10 s 内输出结果，具备实用可行性。

4 结束语

激光系统是目前反无人机的重要手段之一，规划地基激光系统的部署，可使各激光系统的效能得到合理的发挥，提升要地防御能力。本文分析了地基激光系统的特点，建立了对匀速直线飞行目标的毁伤模型，使用粒子群算法实现了部署方案优化过程。结果表明，在本文所建立模型之下，粒子群算法能找到正确的部署优化方向，在3 种不同场景下所得结果均优于圆心式部署和完全随机部署，可为定向能系统反无人机作战研究提供参考。