车载惯导大倾角导航姿态误差的理论分析 *

彭惠，余胜义，王盛，李先慕，慕德

（北京航天发射技术研究所，北京 100076）

0 引言

车载惯导为系统车辆提供定向定位及授时等功能［1］，传统对车载惯导的使用方式多为将车载惯导安装在车大梁上，惯导测量的方位角等导航信息经安装误差标定后传递给系统使用［2］，车载惯导的俯仰角和横滚角为小角度，工作在小倾角（车载惯导工作倾角一般为5°以内）工作状态。然而随着作战方式多样化以及系统精度的不断提升［3-4］，有些系统直接将惯导安装在雷达阵面或者发射架上使用以减少中间的传递误差［5-6］，在这种工作状态下，车载惯导的俯仰角或横滚角一般较大，车载惯导处于大倾角工作状态［7］。

在某次车载惯导大倾角试验中，惯导随转台旋转时，导航输出方位角、横滚角误差比惯导小倾角时明显增大，超出了误差允许范围。本文识别出车载惯导大倾角工作状态时，作为比对基准的转台方位轴的不铅垂度是惯导导航误差的误差源，对其进行了理论推导及试验验证，推导出导航姿态误差与惯导俯仰角及转台不铅垂度的关系公式，为车载惯导大倾角下的使用提供理论参考。

1 惯导姿态角及姿态误差

车载惯导方位角、横滚角及俯仰角的示意如图1 所示。

惯导纵轴（y轴）在水平面的投影与北向的夹角为方位角ψ；惯导y轴与其水平面投影间的夹角为俯仰角α；惯导横轴（x轴）与其水平面投影间的夹角为横滚角β。以东北天坐标系为导航坐标系（n 系），用Oxnynzn表示［8-9］；以右前上坐标系为载体坐标系（b 系），用Oxbybzb表示。n 系经过3 次旋转到b 系，即绕z轴转航向角-ψ（ψ北偏东为正），绕x轴转俯仰角α，绕y轴转横滚角β，旋转获得的姿态矩阵Cnb表征了姿态角的相对关系［10］：

根据车载惯导的应用情况［11-12］，约束方位角取值范围为0～360°，俯仰角和横滚角范围为-90°～+90°，车载惯导获得姿态矩阵后根据式（2）求解出姿态角后上传给整车系统使用。

车载惯导的姿态角误差方程［13-14］为

式中：Φ为惯导姿态角矢量为导航系（n）相对于惯性系（i）的角速率在导航系的投影；[δKG]为陀螺的刻度系数误差矩阵；[δG]为陀螺安装误差角矩阵；εn为陀螺零偏在导航系的投影［15］；为载体系（b）相对于惯性系（i）的角速率在载体系的投影。由式（3）可看出，导航姿态误差主要与安装误差、刻度系数误差以及陀螺零偏有关。

车载惯导安装在转台上，惯导天向轴与转台方位轴基本重合，惯导在经过系统误差标定［16-17］后，陀螺刻度系数误差、安装误差带来的导航姿态误差可忽略［18］。车载惯导随转台绕方位轴旋转，转台旋转角速度为60 （°）/s，旋转一周的时间不大于6 s，因此忽略陀螺零偏带来的导航姿态误差，在此基础上分析惯导大倾角时与转台不铅垂度相关的导航姿态误差。

2 大倾角导航姿态误差分析

2.1 大倾角导航方位角误差分析

车载惯导安装在转台上相对于水平面的俯仰角为α，横滚角为β，其随转台方位轴旋转角度ϕ，转台方位轴相对于水平面不铅垂，设转台相对于水平面存在绕y轴倾斜为Δγ，绕x轴倾斜为Δθ，车载惯导由初始方位的姿态矩阵导航到另一方位的姿态矩阵为之间满足关系：

式中：

由式（8）可见，当转台方位轴铅垂时，车载惯导在导航状态下随转台方位轴旋转角度ϕ时，导航方位角ψ*无误差。但当存在转台方位轴不铅垂时，即Δγ≠0°，Δθ≠0°，为方便分析，令初始时方位角为ψ= 0°，导航方位角度为ϕ*，理论值为ϕ，则有

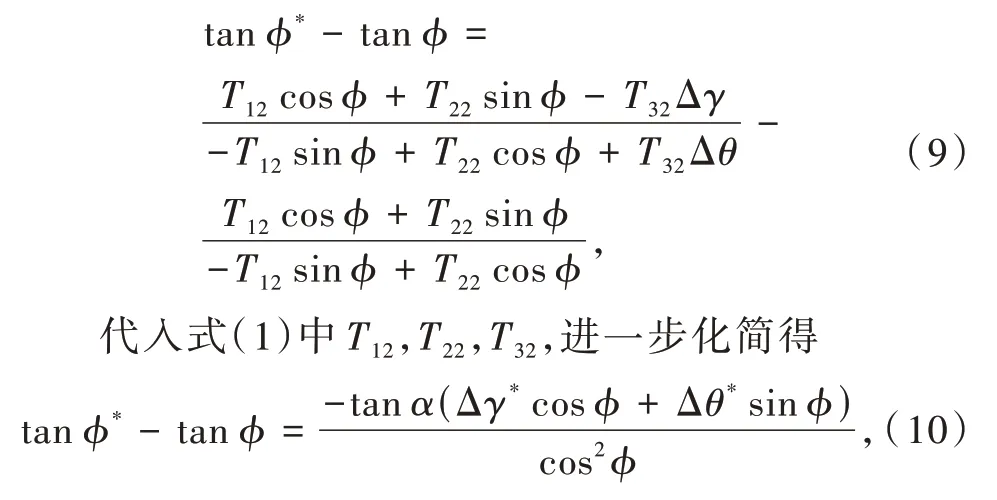
根据泰勒展开公式，式（10）左侧满足：

根据式（9）～（11）可得

通过式（12）可见，转台不铅垂度对车载惯导导航方位角的影响只在大俯仰角工作状态下存在。惯导随着转台旋转时导航方位角误差与惯导俯仰角呈tanα的关系；转台的不铅垂度一定时，俯仰角度越大，导航方位角误差越大；车载惯导工作在小倾角时转台不铅垂度的影响可忽略；车载惯导的导航方位角误差与惯导横滚角大小无关。导航方位角误差呈现360°周期规律，即转台转动整圈（360°的整数倍）时，导航方位角误差与转动开始时的值一致，与转台的不铅垂度无关。

2.2 大倾角导航俯仰角误差分析

按照式（5）求取惯导俯仰角为

由式（13）可见，若Δγ= 0°且Δθ= 0°，车载惯导在导航状态下随转台方位轴旋转角度ϕ时，导航俯仰角无误差。设惯导在导航状态下随转台方位轴旋转角度ϕ后俯仰角为α*，有

令初始时方位角为ψ= 0°，式（14）左右两边展开并化简得

由式（15）可以看出，车载惯导在导航状态下随转台方位轴旋转角度ϕ时，导航俯仰角误差为转台不铅垂度受方位角调制的结果，导航俯仰角误差呈现360°周期规律且与惯导倾角大小无关。

2.3 大倾角导航横滚角误差分析

类似于方位角误差分析，按照式（5）求取惯导横滚角误差为

由式（17）可以看出，若Δγ= 0°且Δθ= 0°时，车载惯导在导航状态下随转台方位轴旋转角度ϕ时，导航横滚角无误差。存在转台不铅垂度时，车载惯导在导航状态下随转台方位轴旋转角度ϕ时，导航横滚角误差与俯仰角间呈的关系。转台不铅垂度一定时，俯仰角越大，导航横滚角误差越大；导航横滚角误差呈现360°周期规律，与横滚角大小无关。

3 仿真分析

3.1 大俯仰角模拟求解与公式计算的对比

设初始方位角ψ= 0°，横滚角β= 0°，俯仰角α为80°，Δγ= 0.03°，Δθ= 0.03°，基于式（4）建立的模型模拟求解惯导以导航角度ϕ间隔10°从0°～360°的导航方位角误差、俯仰角误差及横滚角误差并与所推导的理论公式的计算结果比较，绘制曲线如图2 所示。

图2 俯仰角80°模拟仿真与公式计算对比Fig.2 Comparison between simulation and formula calculation of pitch angle at 80 °

如图2 所示，“公式计算”和“模拟求解”两条曲线的纵坐标均为左侧纵坐标，分别为公式计算和模拟求解的方位角误差、横滚角误差及俯仰角误差，两条曲线基本重合；图1 中“差值”曲线纵坐标为右侧纵坐标，为模拟求解的导航误差与公式计算导航误差的差值。从图2 可以看出，由式（12）估算的导航方位角误差和式（17）估算的横滚角误差与模拟求解的差值最大不超过0.000 6°，俯仰角差的公式估算（式（15））与模拟求解的差值最大不超过0.000 1°。

3.2 大横滚角模拟求解与公式计算的对比

设初始方位角ψ= 0°，横滚角β= 80°，俯仰角α= 0°，Δγ= 0.03°，Δθ= 0.03°，基于式（4）模拟求解导航角度ϕ间隔10°从0°～360°的导航方位角差、俯仰角差以及横滚角差并与理论公式的计算结果进行比较，绘制曲线如图3 所示。

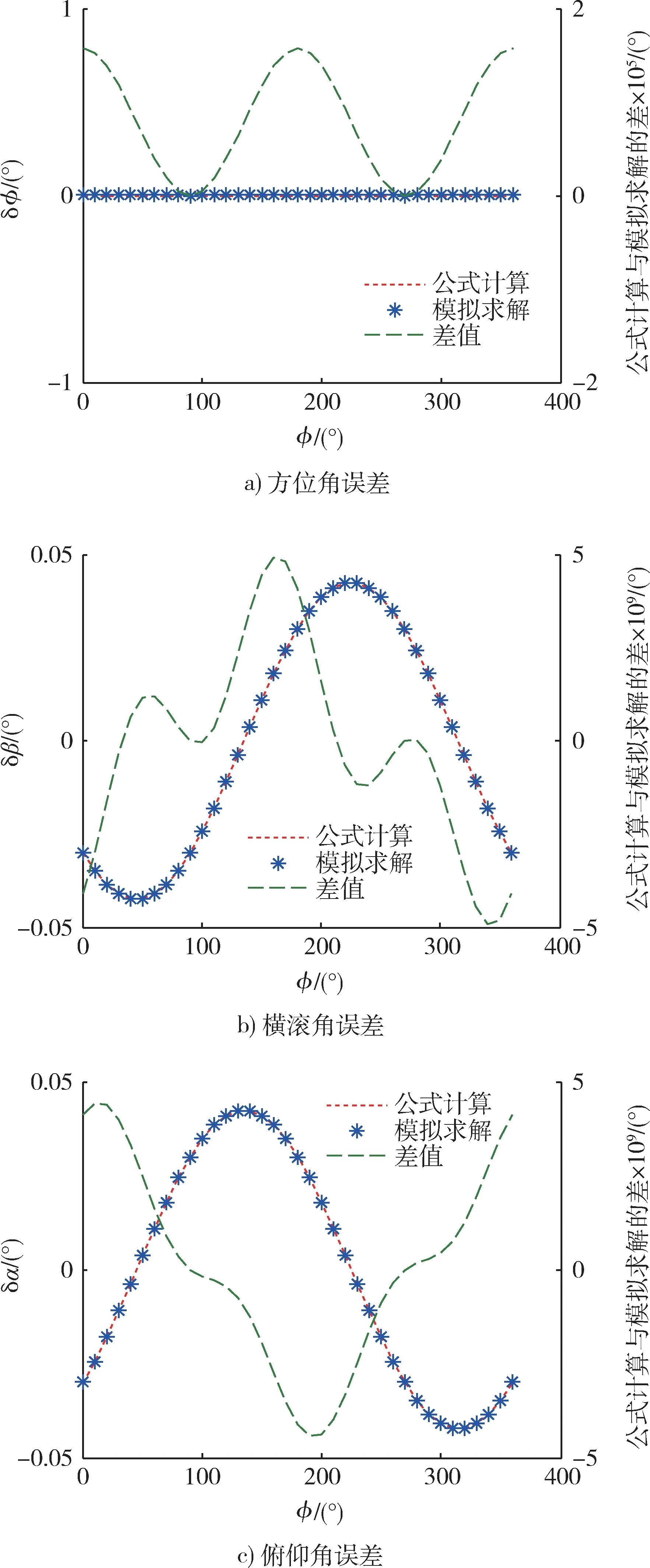
图3 横滚角80°模拟仿真与公式计算结果对比Fig.3 Comparison between simulation and formula calculation of roll angle at 80 °

由图3 所示可以看出，横滚角为80°时，由式（12）估算的导航方位角误差与模拟计算的差值最大为0.000 02°，由式（17）估算的横滚角误差与模拟求解的差值最大为4.4 × 10-9（°），俯仰角差的公式估算（式（15））结果与模拟求解的差值最大为5 ×10-9（°）。

4 实物试验

将车载惯导安装在三轴转台上，控制三轴转台使惯导分别为小倾角0°附近、俯仰角80°附近和横滚角80°附近3 种工作状态。车载惯导在转台方位0°时进行初始对准，对准完成后控制转台绕其方位轴每隔45°旋转，共旋转8 个方位，记录导航方位角、俯仰角及横滚角如表1～3。

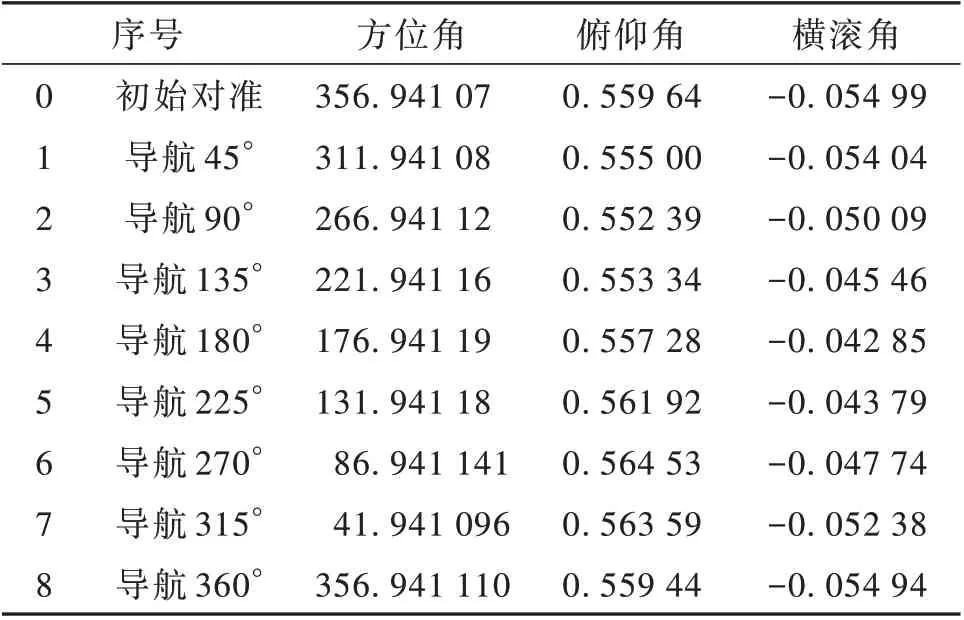
表1 惯导小倾角时的导航姿态角Table 1 Navigation attitude angle of INS with small inclination angles （°）

对比表1～3 可以看出，车载惯导在小倾角时，随转台转动时，导航方位角误差很小，最大约为0.000 12°，俯仰角误差最大约为0.007 2°，横滚角误差最大为0.012°。惯导俯仰角为80°时，每隔45°旋转时方位角误差最大为0.07°，俯仰角误差最大为0.007 5°，横滚角误差最大为0.074°；惯导横滚角为80°时，每隔45°旋转时方位角误差最大为0.003°，俯仰角误差最大为0.008 9°，横滚角误差最大为0.013°。

绘制表1～3 的方位角误差、横滚角误差及俯仰角误差如图4。

图4 导航姿态误差对比Fig.4 Comparison of navigation attitude errors

由图4 可以明显看出，车载惯导在俯仰角为80°时，导航方位角误差和横滚角误差相较于小倾角和横滚角80°时明显增大，方位角误差约为小倾角时的580 倍，为横滚角80°时的20 倍，横滚角误差约为小倾角时的6 倍，为横滚角80°时的6 倍。

对转台进行调平后（调平后转台不铅垂度约为1″），重新进行俯仰角80°时的导航试验，试验数据如表4。

由表4 可以看出，转台调平后，惯导俯仰角80°时导航方位角误差最大为0.004°，横滚角误差最大为0.004 12°，相较于转台调平之前明显减小。根据理论分析结果，导航360°时的惯导方位角应与0°时的值一致，即惯导在随转台转动整圈时，导航的姿态角误差不受转台不铅垂度的影响。但从表2 的实际测试结果来看，惯导初值为356.514 37°，转动一圈后方位角为356.511 21°，与初始对准值相差0.003 16°，这是由于惯导标定后的残余安装误差和残余刻度系数误差导致的。

表2 惯导俯仰角80°时的导航姿态角Table 2 Navigation attitude angle of INS with pitch angle at 80° （°）

5 结束语

本文对车载惯导安装在转台上随转台方位轴旋转时，大俯仰角和大横滚角工作状态下的导航姿态误差进行了理论分析，推导出导航姿态误差与转台不铅垂度及惯导倾角相关的理论公式，同时进行了仿真分析和实物验证，结果表明：

大倾角状态下惯导导航输出的方位角误差是转台不铅垂度受方位调制后乘以俯仰角的正切值，橫滚角误差是转台不铅垂度受方位调制后除以俯仰角的余弦值。车载惯导在大俯仰角下工作时，若转台方位轴不铅垂，俯仰角越大惯导随转台方位轴旋转时导航方位角误差和横滚角误差越大，导航俯仰角误差与惯导的俯仰角大小无关。转台不铅垂度一定的情况下，惯导俯仰角80°时方位角误差为小倾角时的583 倍，为横滚角80°时的23 倍。惯导俯仰角80°时横滚角误差约为小倾角和惯导横滚角80°时的6 倍。车载惯导的导航姿态误差在大俯仰角时明显增大，与惯导横滚角大小无关。车载惯导随转台转动360°时，导航姿态误差不受俯仰角大小及转台不铅垂度的影响，仅与车载惯导标定后残余安装误差及残余刻度系数误差有关。

本文的理论公式推导基于惯导初始方位角为0°进行的，车载惯导初始方位角为其他角度的情况限于篇幅未能进一步推导与分析，如果惯导初始方位角为其他角度，可参考本文的分析方法进行进一步推导与分析。