多无人水下航行器协同探测声呐宽带波形设计与性能分析
2023-11-18许彦伟刘明刚郝程鹏王佳欢周正春
许彦伟 薛 勐 刘明刚 郝程鹏* 赵 莉 王佳欢 周正春
①(中国科学院声学研究所 北京 100190)
②(中国科学院大学 北京 100049)
③(西南交通大学 成都 611756)
1 引言
随着无人水下航行器(Unmanned Underwater Vehicle,UUV)相关技术的快速发展,单一UUV面临着冗余性差、任务范围小和工作效率低等局限性[1],单UUV探测声呐已很难满足复杂海洋环境水下勘探或侦测任务需求。虽然多用户协同探测(Multip le User Detection,MUD)技术已应用于雷达和声呐,但目前大部分MUD技术的研究重点是信号检测[2–6]或信道估计[7,8],缺少对多址波形设计的进一步研究。同时,相比于利用电磁波探测目标的雷达,声呐的工作频率低、带宽窄,声波的传播速度慢,受多普勒效应影响大,在波形分析与信号处理时难以满足窄带条件,需要基于宽带模糊函数和宽带信号处理方法对其进行分析和处理。如何基于宽带信号处理技术,设计具有大多普勒容限、良好的自相关与互相关性能以及抗混响能力的发射信号波形,是提升多UUV协同探测声呐性能的重要途径[9,10]。然而,复杂海洋环境下的水声信道往往具有时间扩展、频率扩展或时频双扩展特性[11–13],使得时分多址(Time Division M ultip le Access,TDMA)波形和频谱效率较低的频分多址(Frequency Division M u ltip le A ccess,FDM A)波形很难应用到多UUV协同探测声呐中。而码分多址(Coding Division M ultip le Access,CDMA)技术可以有效弥补FDMA和TDMA应用在水声探测中的不足,实现扩展水声信道下多UUV协同探测声呐的多址容量和频谱效率提升。
CDMA雷达或声呐需要利用正交波形进行目标探测,研究较多的主要有正交多相码、正交离散频率编码(Discrete Frequency Coding W aveform,DFCW)等波形[14–16]。针对DFCW,文献[17]对单个DFCW进行了分析,文献[18,19]采用了遗传算法、循环算法等方法设计了不同编码方式的DFCW,但当存在多普勒频移时其性能会有较大的下降,文献[20]设计了多普勒容限有所改善的正交相位编码波形,文献[21]提出了一种运算量较小的快速波形优化方法,文献[22]采用空时编码提高了信号的自相关与互相关性能。上述方法设计的波形主要对波形自相关与互相关性能进行了改善,但对多普勒效应敏感,不利于运动目标检测。文献[15]对线性调频(Linear Frequency M odulation,LFM)信号的互相关函数进行分析,指出当频谱不重叠时发射信号间的互相关值较小,但其自相关受线性调频信号的限制旁瓣较高。文献[23]提出了一种非均匀间隔的正交频分线性调频(Orthogonal Frequency Division Linear Frequency M odulation,OFD-LFM)波形设计方法,使得信号具有较大的多普勒容限。这些方法设计的波形一定程度上改善了雷达信号对运动目标检测的性能,但由于声波的特殊性,无法被直接应用在声呐中。因此,针对多UUV协同探测声呐对抗多普勒效应、抗混响多址波形的需求,本文基于OFD-LFM以及Costas[24,25]伪随机序列,设计了离散频率编码正交线性调频波形(Discrete Frequency Coding W aveform of Orthogonal Frequency Division Linear Frequency M odu lation,DFCW-OFD-LFM)和非均匀频率间隔的离散频率编码非正交线性调频波形(D iscrete F requency Coding W aveform of Non-Orthogonal Frequency Division Linear Frequency M odu lation,DFCWNOFD-LFM),并利用宽带模糊函数和Q函数等评价工具对波形的性能进行了理论与仿真分析,结果表明,相比于二进制相移键控(Binary Phase Shift Keying,BPSK)和DFCW等传统CDMA信号波形,本文所研究设计波形具有大多普勒容限、良好的自相关与互相关性能和优秀的抗混响性能。
2 伪随机编码信号模型及理论分析
信号的相关函数可以反映波形的自相关与互相关特性,信号的模糊函数可以反映波形的时间和多普勒分辨力(即距离和速度分辨力)。由于UUV与其探测目标之间可能具有较高的相对速度,并且多UUV探测声呐信号波形需要较大的带宽,传统窄带模糊函数分析方法难以适用宽带UUV探测波形分析,需要利用宽带模糊函数,其计算方式如式(1)[26]所示,其中,t表示信号发射时间,τ表示时延,η表示多普勒压缩因子
2.1 BPSK信号
CW信号可以表示为
信号sCW(t)的自相关函数和宽带模糊函数分别如式(4)和式(5)所示,其中,|τ|≤Tp
信号sBPSK(t)的自相关函数和宽带模糊函数可通过CW信号的自相关函数和宽带模糊函数表示,分别如式(6)和式(7)所示。其中,式(6)的第1项为主瓣形成前各子波的互相关积分和,形成左旁瓣,第2项为各子波的自相关积分和,即主瓣,第3项为主瓣形成后各子波的互相关积分和,形成右旁瓣。由式(6)可看出,由于RCW(τ)形状不变,左旁瓣和右旁瓣的大小主要与伪随机序列有关,其随机性越好,旁瓣值越小
2.2 DFCW信号
DFCW信号模型如式(8)所示
其中,T表示信号发射脉宽,N表示子信号个数,c n表示频率调制序列码第n个码元,f0表示信号的起始频率,信号的总带宽为B,Tp=T/N为子信号的脉宽,频率间隔Δf=B/N,f0+(c n-1)Δf表示第n个子信号的起始频率。
子信号的互相关函数和宽带互模糊函数分别如式(10)和式(11)所示,式中,f n=f0+(c n-1)Δf,fm=f0+(c m-1)Δf,cn和c m分别表示频率调制序列码第n个码元和第m个码元,|τ|≤Tp
想客人之所想,急客人之所急,往往是企业树立良好形象的关键。恰到好处的个性化服务能使顾客真切感受到酒店的关怀,体会到酒店以顾客利益为重,这样友好、周到的酒店形象便可深入人心。
信号sDFCW(t)的自相关函数和宽带模糊函数分别如式(12)和式(13)所示。其中,式(12)的第1项为会形成左旁瓣的各子波互相关积分和,第2项为形成主瓣的各子波自相关积分和,第3项为会形成右旁瓣的各子波互相关积分和。由式(12)可看出,RDFCW(τ)左旁瓣和右旁瓣大小主要子波之间的互相关以及它们的互相关和有关。由于DFCW的子波之间不能保证正交,所以RDFCW(τ)的左旁瓣和右旁瓣较大
2.3 DFCW-OFD-LFM信号
DFCW-OFD-LFM信号模型如式(14)所示,其调频方式可在(t,f)平面上用图1所示的网格图等价表示
其中,T表示信号发射脉宽,N表示子信号个数,c n表 示Costas序列的第n个码元,Tp=T/N表示子信号的脉宽,子信号之间的频率间隔Δf=M/Tp,M为正交频率间隔系数,一般为自然数,k=Bs/Tp表示子脉冲LFM信号的调频斜率,Bs为子信号的带宽,Bs≤B-(N-1)Δf。
子信号s n(t)和sm(t)的互相关函数和宽带互模糊函数分别如式(16)和式(17)所示,γ=f n-f mkτ,µ=f nη-f m-kτ,fn为 子信号sn(t)的起始频率,f m为 子信号s m(t)的 起始频率,|τ|≤Tp
信号sDFCW-OFD-LFM(t)的自相关函数和宽带模糊函数分别如式(18)和式(19)所示,同样地,式(18)中第1项为会形成左旁瓣的各子波的互相关积分和,第2项为形成主瓣的各子波的自相关积分和,第3项为会形成右旁瓣各子波的互相关积分和。由于DFCW-OFD-LFM各子波之间相互正交,所以,相比于非正交的子波,RDFCW-OFD-LFM(τ)在一定程度上抑制了栅瓣
2.4 DFCW-NOFD-LFM信号
文献[27]指出,对于OFD-LFM波形,子波之间相同的频率间隔会造成同频相加的情况,进而自相关函数式(18)以及宽带模糊函数式(19)都存在较高的栅瓣,因此,考虑在子波之间设置非均匀的频率间隔和初始相位,并可以针对特定应用场景进行针对性优化,该方法降低了子波之间的正交性,但能够在一定程度上抑制栅瓣。
DFCW-NOFD-LFM信号模型同DFCW-OFDLFM,如式(20)所示
其中,T表示信号发射脉宽,N表示子信号个数,Tp=T/N表示子信号的脉宽,cn表示Costas序列第n个码元,每组Costas序列中存在第i个子信号对应的码元ci-1=0,表示该子信号的起始频率在信号的起始频率,因此,第n个子信号与第n+1个子信号之间的频率间隔Δf n=M n/Tp,M=[M1,M2,...,M N-1]为频率间隔系数序列;k=Bs/Tp表示子脉冲LFM信号的调频斜率,B为信号的总带宽,Bs为子信号的带宽,Bs≤B-(N-1)·max{Δf n},φn为子信号的初始相位,φn∈[0,2π],Φ=[φ1,φ2,...,φN]为初始相位序列。
子信号s n(t)和sm(t)的互相关函数和宽带互模糊函数分别如式(22)和式(23)所示,其中,γ=f nf m-kτ,µ=f nη-f m-kτ,fn为子信号sn(t)的起始频率,fm为子信号sm(t)的起始频率,|τ|≤Tp
由于DFCW-NOFD-LFM只改变了DFCWOFD-LFM中每个子信号的起始频率和初始相位,因此自相关函数与宽带模糊函数的形式都与后者相同,此处不再赘述。
3 伪随机编码波形特性分析
基于水下目标检测的应用场景,假设信号总脉宽T ≤100m s,系统可用带宽B≤5 kHz,可用频带起始频率为10 kHz,终止频率为15 kHz,UUV数量为6。BPSK信号采用127 bit Gold序列进行相位调制,子信号脉宽Tp=T/N ≈0.787 m s。DFCW信号采用7阶Costas序列对其频率进行调制,子信号脉宽Tp=T/N ≈14.3 m s,频率间隔Δf=B/N=5/7 kHz;DFCW-OFD-LFM和DFCW-NOFDLFM同样采用7阶Costas序列对信号频率进行调制。对于等频率间隔的DFCW-OFD-LFM,在自然数中选取性能较好的M0=8作为频率间隔系数,进而等频率间隔Δf=M0/Tp=560 Hz,子信号之间具有正交性,Bs=B-(N-1)Δf=1640 Hz。而对于非均匀频率间隔的DFCW-NOFD-LFM,利用遗传算法搜索(计算精度为10-6)得到频率间隔系数序列M =[7.278 223,7.839 019,7.203 638,7.098 962,7.559 781,8.062 531]和初始相位序列Φ=[5.135 079,2.002 259,1.315 504,5.125 971,0.328 277,5.171 224,2.627 270],实现多UUV探测声呐波形非等均匀间隔的频率调制以及初始相位优化;遗传算法一般用于求解较为复杂的组合优化问题,其从串集开始搜索,使用模糊自适应法在进化过程中自动调整算法控制参数和编码精度,覆盖面大,利于全局择优;子信号脉宽Tp=T/N ≈14.3m s,子信号间的频率间隔Δf n=M n/Tp,子信号之间不再具有正交性,Bs=B-(N-1)·m ax{Δf n}≈1 614 Hz。
下面对基于以上应用环境和仿真条件的各伪随机编码波形的宽带特性进行仿真分析。
3.1 宽带模糊函数
图2为DFCW-OFD-LFM和DFCW-NOFDLFM的宽带模糊函数图和模糊度图,相比于模糊函数图像为图钉型的BPSK和相关峰旁瓣较高的DFCW,DFCW-OFD-LFM同时具有较高的时间和频率分辨力,同时对多普勒不敏感,但缺点是在时间轴上存在较多的栅瓣,会对多目标探测形成一定的干扰,而DFCW-NOFD-LFM通过非均匀频率间隔和初始相位优化,一定程度上压制了栅瓣。

图2 T =100 m s,B ≤ 5 kHz时各波形宽带模糊函数图和模糊度图
3.2 自相关与互相关性能
为了比较各波形的自相关与互相关性能,本文对各波形的自相关旁峰(Au to-correlation Side Peak,ASP)和互相关峰(Cross-correlation Peak,CP)结果进行了仿真统计,统计结果如表1所示。
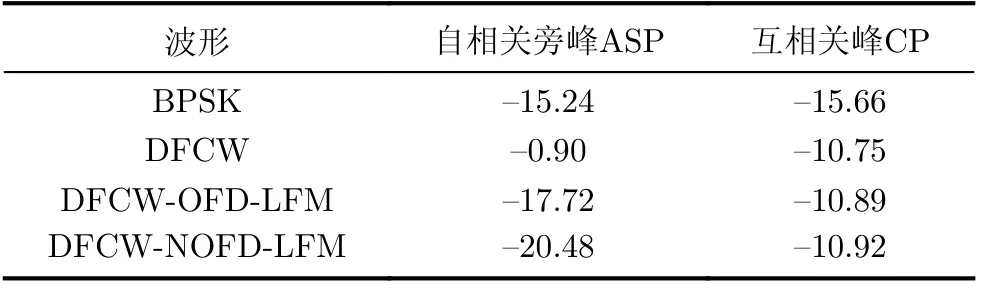
表1 各波形的自相关旁峰与互相关峰(dB)
由表1可知,BPSK同时具有较低的自相关旁峰和互相关峰;而DFCW的自相关旁峰很高,互相关峰较低;DFCW-OFD-LFM具有很低的自相关旁峰,约为–17.72 dB,互相关峰较低,约为–10.89 dB;DFCW-NOFD-LFM具有更低的自相关旁峰和互相关峰,分别约为–20.48 dB和–10.92 dB。
3.3 多普勒敏感性分析
本文对各波形在不同多普勒速度的自相关性进行了统计,统计标准为:自相关主瓣距离分辨力在2 m之内且主旁瓣比在3 dB(旁瓣在主瓣2 m以外)以上,本文认为能够检测到该速度的目标,否则为不能检测该速度目标的回波信号。结果表明,BPSK对多普勒特别敏感,只有在0 kn时才能检测出信号,稍有多普勒速度(1 kn以上)就无法检测出信号;由于DFCW的主瓣很宽,其距离分辨力很低,水下目标检测所需要的距离分辨力超出该波形的距离分辨力,其旁瓣峰也较高,因此按照统计标准,即使在0 kn,其主瓣距离分辨力也在45 m左右,所以很难按要求检测出目标回波信号;而DFCW-OFDLFM在相对速度不大于20 kn时,都能准确地检测出目标回波信号,当相对速度35~40 kn时,也能检测出目标回波信号,只是由于栅瓣干扰,其主瓣距离分辨力降到3 m左右;而DFCW-NOFD-LFM在一定程度上解决了栅瓣的干扰,得到最好的检测结果。
接下来使用峰值旁瓣比(Peak Side Lobe Ratio,PSLR)和积分旁瓣比(Integral Side Lobe Ratio,ISLR)对波形进行了分析,PSLR值越低,低强度目标的主瓣越不容易被邻近强目标的旁瓣淹没,ISLR值越低,暗回波区越不容易被邻近强散射区所影响,各波形在不同多普勒速度时对应的PSLR值和ISLR值如表2所示。为进一步分析各波形的多普勒敏感性,DFCW-OFD-LFM和DFCW-NOFDLFM在不同多普勒速度时对比BPSK的脉冲压缩图如图3所示。
由表2和图3可知,DFCW-NOFD-LFM具有最小的PSLR值和ISLR值,0 kn时分别约为–20.48 dB和–1.93 dB,在检测低强度目标时具有更好的优势;DFCW-OFD-LFM比较DFCW与BPSK,也具有更小的PSLR值和ISLR值,0 kn时分别约为–17.72 dB和–1.16 dB。
3.4 抗混响性能(Q函数)
Q函数为模糊函数在时延轴方向上的积分,可以体现各波形在不同多普勒速度上的抗混响性能,Q函数的计算方式如式(24)所示。Q函数越小表示信号的抗混响性能越好
图4为各波形的Q函数图,可以看出DFCWOFD-LFM和DFCW-NOFD-LFM在–60~60 kn范围内都具有较好的抗混响性能;BPSK的抗混响性能整体上是比较不好的;而DFCW在–10~10 kn时,抗混响性能较差,而相对速度超过10 kn时,抗混响性能较好。
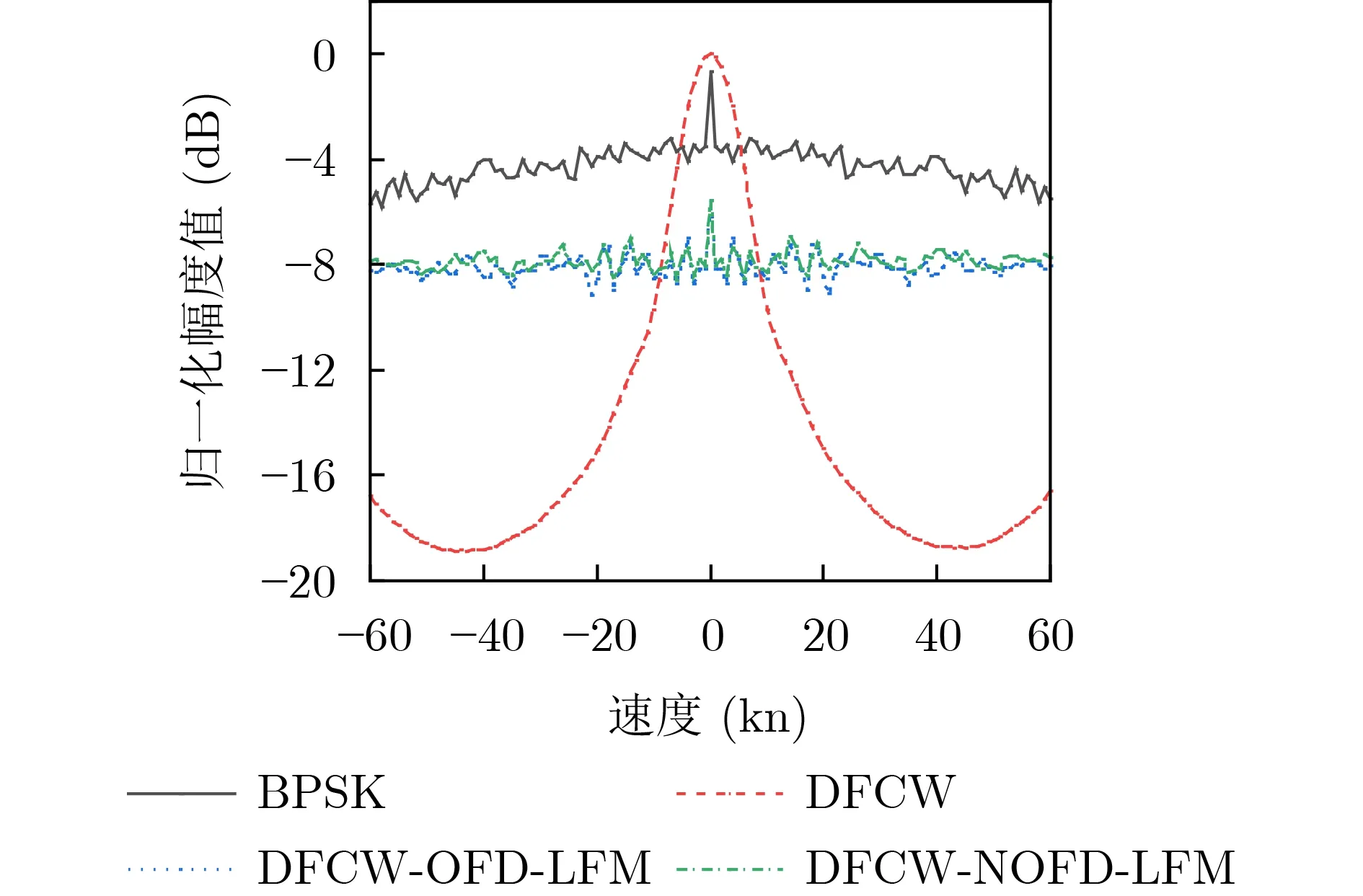
图4 T =100 m s,B ≤ 5 kHz时各波形Q函数比较
4 结束语
本文基于Costas序列和OFD-LFM波形,设计了DFCW-OFD-LFM和DFCW-NOFD-LFM。理论分析与仿真结果表明,相比于传统BPSK和DFCW等波形,本文所设计的DFCW-OFD-LFM和DFCWNOFD-LFM,具有多普勒容限大、抗混响能力强的优点。而由于子波同频相加,DFCW-OFD-LFM的自相关函数存在栅瓣问题,基于遗传算法等对子波频率间隔和初相优化后的DFCW-NOFD-LFM,对以上问题进行了初步的改善。下一步将对所设计波形进行更针对性的优化和工程验证。
