Gim li/Xoodoo密码算法的不可能差分分析
2023-11-18韦永壮李灵琛
樊 婷 韦永壮李灵琛
(桂林电子科技大学广西密码学与信息安全重点实验室 桂林 541004)
1 引言
2018年8月,美国国家标准与技术研究院(National Institute of Standards and Technology,NIST)开始征集轻量级密码算法,接受面向资源受限环境下带关联数据的轻量级认证加密(Authentica ted En cryp t ion w ith A ssocia ted D a ta,AEAD)和哈希方案的投稿,在2019年8月、2021年3月分别公布了进入第2、第3轮的候选算法[1–3]。许多方案以大状态密码算法作为底层置换,如384 bit的Gimli[4],320 bit ASCON[5],非线性部件采用64 bit A lzette盒的Spark le[6]以及与Keccak-p[7]置换结构类似的Xoodyak[8]等。其中,Gim li置换是由Bernstein等人[4]在CHES 2017(Cryp tographic Hardware and Embedded System s 2017)首次提出,基于Gim li置换的哈希方案(Gim li-Hash)和带有关联数据的认证加密方案(Gim li-AEAD)是NIST轻量级加密算法项目第2轮的候选方案[9]。Xoodoo置换是Daemen等人[10]在FSE 2018(Fast Software Encryption 2018)提出的一种新型置换结构,其设计受到Keccak-p置换的启发。Gim li和Xoodoo置换的规模相同,二者实现性能出色、抵抗侧信道攻击能力强,在嵌入式系统、RFID、传感器网络等物联网环境下,成为同时满足安全性和性能要求的可选方案。
迄今为止,Gim li和Xoodoo置换安全性问题吸引了很多密码学者的关注。在差分类分析方面,Liu等人[11]在美密会(CRYPTO 2020)发表的论文中提出了自动化检测差分路径有效性的混合整数线性规划(M ixed Integer Linear Programm ing,M ILP)模型,搜索到6轮Gim li有效差分路径,同时给出满足差分路径的消息对。2022年,谭豪等人[12]针对G im li提出一个差分传播系统,找到了可应用于Gim li-AEAD的7轮不可能差分路径,对11轮带有关联数据的Gim li-AEAD进行攻击。在Xoodoo安全性分析方面,欧密会(EUROCRYPT 2021)会议发表的论文对差分-线性分析进一步扩展,确定了Xoodoo置换一个相关性为1的4轮旋转差分-线性区分器[13]。2022年,一种使用可满足性模理论(Satisfiability Modulo Theories,SMT)构造有效差分路径的方法被Bellini等人[14]提出,寻找到多条3轮最优差分路径。Gim li置换存在弱扩散性的特点,而针对Xoodoo以及基于Xoodoo置换的方案,大多处于低轮次的攻击。那么,Gim li和Xoodoo置换是否存在更高轮的不可能差分区分器,以及二者是否能抵御不可能差分密码分析仍亟待进一步研究。
鉴于上述存在的问题,本文基于Gim li/Xoodoo密码算法的结构特点,研究了这两个算法非线性操作与S盒之间的关系,给出二者的等价表示;针对非线性操作转化后的几类S盒,利用M ILP技术进行建模,提出了用于Gim li/Xoodoo密码算法的不可能差分分析自动化分析模型。此外,为了验证区分器的正确性,本文结合“二分法”思想,给出了一种用于检测不可能差分区分器矛盾点的新方法。该方法能够快速定位矛盾点,具备高效验证区分器正确性的优势。结果表明:Gim li存在10轮不可能差分区分器;Xoodoo存在4轮不可能差分区分器。与已有结果相比,Gim li的新不可能差分区分器轮数提高了3轮。
后续章节组织如下,第2节描述Gim li/Xoodoo算法的具体步骤;第3节介绍基于M ILP面向比特的不可能差分区分器搜索模型;第4节阐述G im li/Xoodoo中非线性操作与S盒之间的等价表示;第5节给出Gim li和Xoodoo置换不可能差分区分器以及检测矛盾位置的新方法,第6节进行总结。
2 算法介绍
2.1 符号说明
符号表示如表1所示。

表1 符号说明
2.2 Gim li算法
入和输出。SP盒操作表达式为
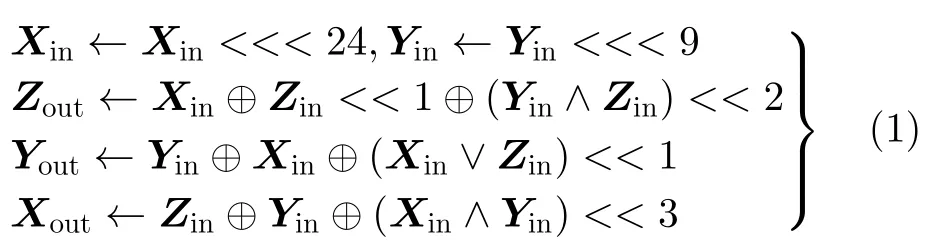
进一步,得到(Xout,Yout,Zout)和(Xin,Yin,Zin)之间关系为
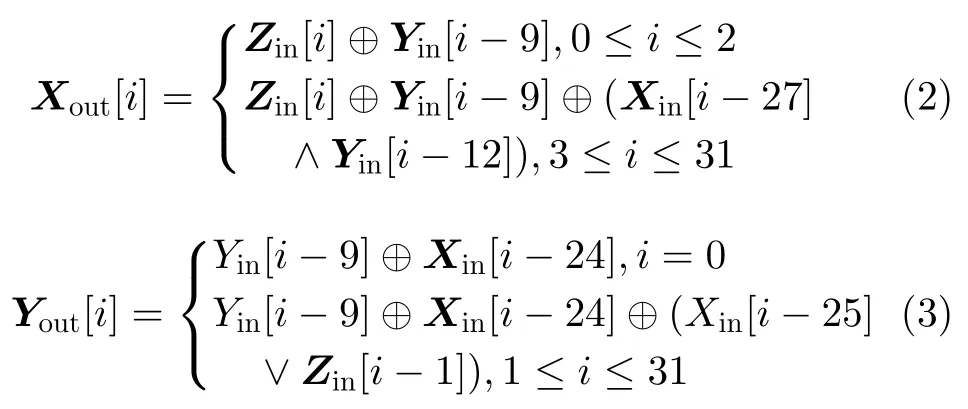
2.3 Xoodoo算法
X oodoo算法状态大小与G im li相同,即 SX=384,分布在4× 3× 32的状态矩阵中(如图2所示),SX=(S x,y)(0≤x≤3,0≤y ≤2),每个字长度为32 b it,即Sx,y ∈F232×3,共迭代12轮(-11≤r ≤0),轮函数被定义为FX=ρeast◦χ ◦τ ◦ρwest◦θ,其中χ是唯一的非线性部件,5个步骤具体定义为
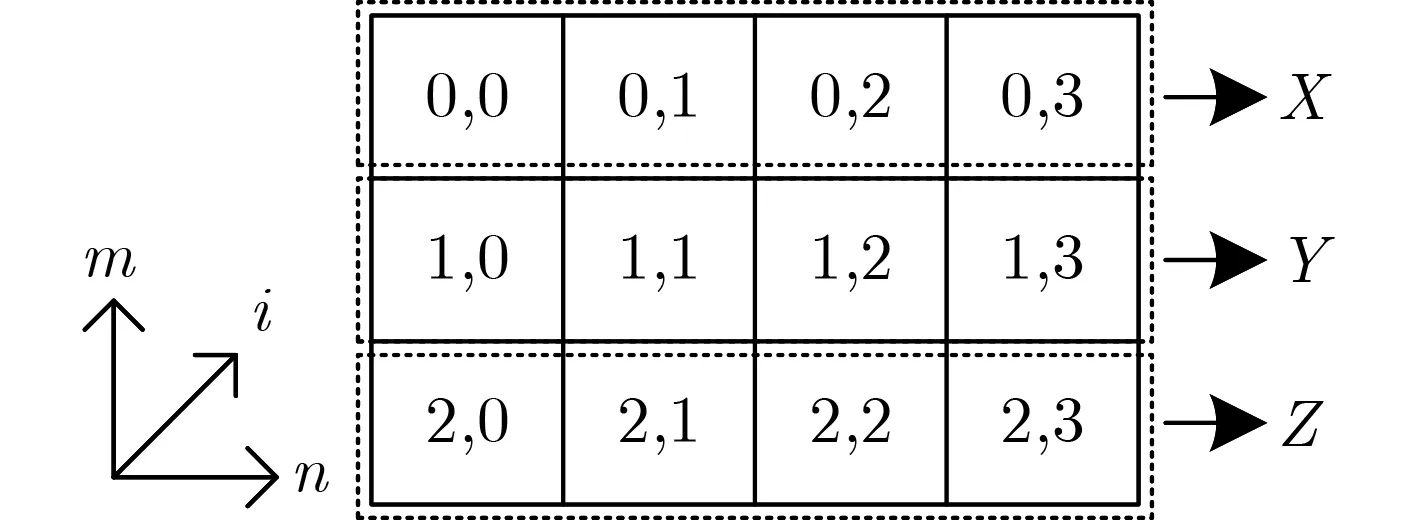
图1 Gim li状态矩阵
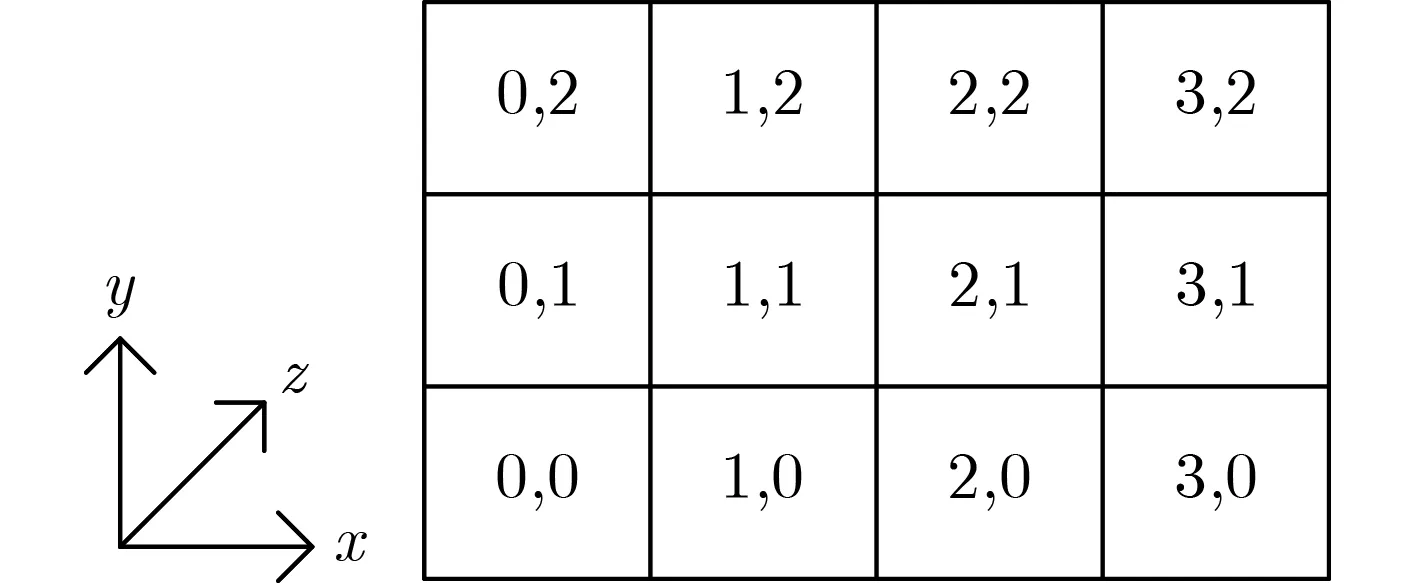
图2 Xoodoo状态矩阵
3 基于M ILP面向比特的不可能差分模型
M ILP模型用于解决最优化问题,在密码学分析领域,可将密码算法安全性分析问题转化为M ILP问题。总的来说,是用不等式约束条件表示线性、非线性操作,求目标函数的最优解。对于不可能差分搜索模型而言,不需要设定目标函数,只需固定输入和输出差分,然后在特定的约束条件下,观察模型是否有解。若模型无解,则为不可能差分。接下来,主要介绍不可能差分分析模型中线性操作和非线性操作的建模。
(1)I型XOR操作。对于a ⊕b=c(a,b,c都表示单比特),用式(6)约束条件表示
(2)II型XOR操作。对于a ⊕b ⊕c=d(a,b,c,d都表示单比特),用式(6)约束条件表示
(3)线性操作。线性操作一般包括循环移位、移位和交换操作等,可用线性等式有效地描述。以G im li中SP盒的循环移位操作“<<<”为例,设Gim li一个字的输入差分为x=(x31,x30,...,x0),经过循环左移24 bit后,输出差分为y=(y31,y30,...,y0),约束条件为
(4)S盒操作。考虑差分值通过S盒的传播性质,用Sun等人[15]提出的凸壳H-Representation(通过线性(不)等式切割欧拉空间获得的多面体)。设x=(x0,x1,...,x p),p=w+v(其中w和v分别是S盒的输入和输出规模)是p维可能的差分模式。则可用以下m个不等式约束条件来表示,其中a i,j(0≤i≤m-1,0≤j ≤p-1)是SageM ath[16]生成的二进制系数
(5)额外条件。限制输入输出差分均只有1 bit或1 个S 盒活跃,即添加2 种额外约束条件,(x0,x1,...,x n)=0 和(x0,x1,...,x n)r=0。其 中,(x0,x1,...,x n)r是初始输入差分(x0,x1,...,x n)经过r轮迭代后的输出差分,n为分组长度。
4 非线性操作与S盒的等价表示
在本节中,主要介绍如何将Gim li算法的SP盒、Xoodoo算法的χ操作等价表示为几类常规S盒(即输入为wbit,输出规格为vbit),给出每一种S盒替换表。
4.1 Gim li算法SP盒等价表示
G im li置换的非线性操作SP盒与普通w×v的S盒不同,它包含循环移位、异或、移位、与操作和或操作。观察式(2)—式(4),进行分解,SP盒等价表示为3种S盒(S1,S2,S3)和一个线性操作,如图3所示。
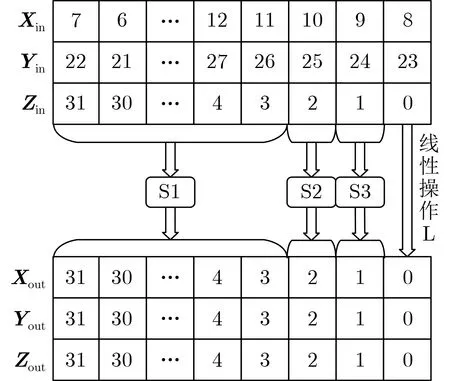
图3 Gim li置换SP盒等价表示
S1,S2,S3盒和线性运算L表达式分别为
S2盒。当i=2时,S2盒规模为7进3出,(A,B,C,D,E,F,G)为7 bit输入,(Zout,Yout,Xout)为3 bit输出。遍历7 bit输入(0000000~1111111),计算对应的3 bit输出,则得到S2盒置换表。
S3盒。当i=1时,S1盒规模为5进3出,(A,B,C,D,E)为5 bit输入,(Zout,Yout,Xout)为3 bit输出。遍历5 bit输入(00000~11111),计算对应的3 bit输出,则得到S3盒置换表,如表2。

表2 S1,S2和S3盒置换表3 bit输出
4.2 Xoodoo算法χ 操作等价表示
χ是Xoodoo中唯一的非线性运算,包含AND操作。将χ看作一个3进3出的S盒,遍历3 bit输入SX[x][y][z] ,S X[x][y+1][z],S X[x][y+2][z]的值,计算相应的输出值,形成的3 bit对合S盒如表3所示。

表3 Xoodoo算法操作χ 的S盒表示
5 Gim li和Xoodoo的具体应用
本部分首先构建基于M ILP技术的Gim li/Xoodoo算法不可能差分区分器自动化搜索模型。对非线性操作建模主要是将转化后的几类S盒,构建差分分布表(Difference Distribution Table,DDT)。再将DDT表中所有可能的差分传播模式放入SageM ath软件,调用sage.geometry.polyhedron中的不等式生成函数,将所有可能的输入输出差分模式表示为一个不等式系统。对线性操作建模参考文章第3节列出的不等式约束。最后,本文提出一种检测矛盾点的新方法,从而验证不可能差分区分器的正确性。
5.1 Gim li算法不可能差分区分器搜索模型
Gim li轮函数包含4种操作:移位、SP盒、2种Swap、轮常数加,这里不考虑轮常数的影响。以下涉及的所有变量都表示状态差分,假设ΔSGr[m][n][i] 和ΔSGr-1[m][n][i]分 别是第r轮的输入差分和输出差分。本部分若无特殊说明,m,n,i的取值范围为0≤m≤2, 0≤n≤3, 0≤i≤31。
(1)非线性操作SP盒约束条件。由在4.1节可知,对SP盒建模等价于对S1盒、S2盒、S3盒和线性操作L分别进行建模。注意到,虽然S1盒的规模大,维度高,元素数量多,但仅用12个不等式就可以表示S1的差分传播过程。S1盒、S2盒、S3盒和线性操作L的约束条件分别为
(2)线性操作约束条件。Gim li算法的线性操作包括移位、SmallSwap和BigSwap。3种操作都可用等式约束条件进行刻画,细节请参考第3节中“线性操作”的约束条件表示。
(4)模型求解。将所有不等式约束条件放入Gurobi[17]求解器,若M ILP模型无解,得到一条Gim li的10轮不可能差分区分器,以十六进制按状态矩阵表示为
5.2 Xoodoo算法不可能差分区分器搜索模型
Xoodoo轮函数共包含5个操作:线性层θ、循环移位ρwest、轮常数加τ、非线性层χ和循环移位ρeast。这里不考虑轮常数加操作τ的影响,只需要对线性层θ、循环移位ρwest、非线性层χ和循环移位ρeast4个操作进行建模,下面将分别进行介绍。以下涉及的所有变量都表示状态差分,ΔSXr[x][y][z]和 ΔSXr+1[x][y][z]分 别是第r轮和r+1轮的输入差分,M1[x][z],M2[x][j][z],N3[x][j][z]都是生成的中间状态变量。本部分若无特殊说明,x,y,z的取值范围为0≤x≤3, 0≤y,j≤2, 0≤z ≤31。
(1)线性层θ约束条件。根据θ操作的定义式,分为3步,首先将输入差分初始状态的3个平面进行叠加,然后将叠加后的平面进行循环移位,最后与输入差分的初始状态异或,得到经过θ操作后的中间状态。∑
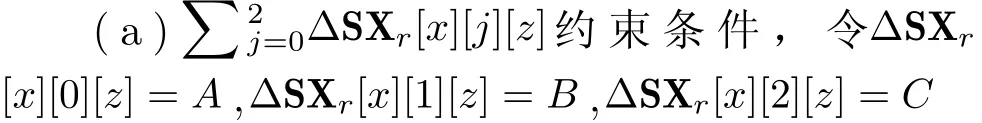
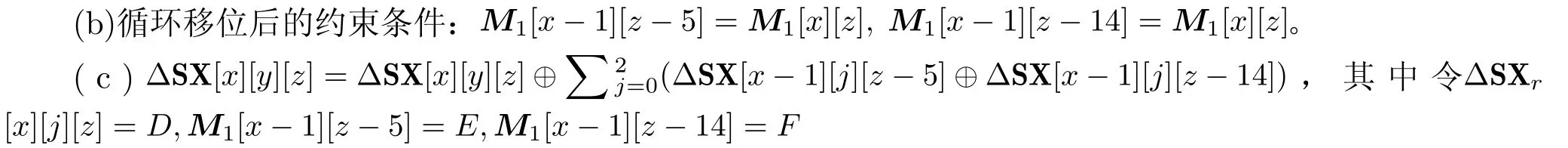
(2)循环移位ρwest约束条件。循环移位首先以字作为单位进行位置变换,再基于比特进行变换。只改变状态差分的位置,不产生新的差分变量:M2[x][1][z]=M2[x-1][1][z],M2[x][2][z]=M2[x][2][z-11]。
(3)非线性层χ约束条件。状态矩阵中的元素以3 bit为一列进行状态更新,更新时差分值会发生改变,产生新差分变量。在步骤(1)和步骤(2)的基础上,生成4.2节提出的非线性层χ的等价S盒DDT表,用3 bit S盒的约束条件来描述非线性操作χ,为了方便表示,令M2[x][0][z]=P,M2[x][1][z]=Q,M2[x][2][z]=T,N3[x][0][z]=X,N3[x][1][z]=Y,N3[x][2][z]=Z。
(4)循环移位ρeast约 束条件。Δ SXr+1[x][1][z]=N3[x][1][z-1], Δ SXr+1[x][2][z]=N3[x-2][2][z-8]。
(5)额外条件。添加3个额外约束条件,即输入差分Δ SX-11[1][0][0]=1 ,Δ SX-11[1][1][0]=1和输出差分ΔSX-7[1][0][0]=1。
(6)模型求解。将所有不等式约束条件放入Gurobi求解器,若M ILP模型无解,得到一条Xoodoo的4轮不可能差分区分器,以十六进制按状态矩阵表示为
5.3 矛盾点验证
对于Gim li/Xoodoo等大状态密码算法,由于状态较大时,矛盾点之间可能具有依赖性,它们不是独立的,使用Cui等人[18]逐条删除比特间的联系无法找到矛盾点。所以,本节给出了一个基于“二分法”思想的新验证算法。该算法分为2步,第1步划分区间,判断矛盾点所在区间;第2步在第1步寻找的区间中确定矛盾点的具体位置,遍历矛盾点位置的取值,查看解的集合。
假设搜索到分组长度为nbit的密码算法一条r轮不可能差分区分器Δin→Δout,那么在[r/2]轮和[r/2]+1轮之间一般存在矛盾点。令α=(α0,α1,...,αn-1)表 示[r/2]的 输出差分,第[r/2]+1的输入差分表示为β=(β0,β1,...,βn-1)。寻找矛盾点时,直接删除(α0,α1,...,αn-1)=(β0,β1,...,βn-1)中的某些不等式,若删除后,该模型由无解变为有解,可判定该中间变量所在的比特位置即为矛盾点。具体验证算法见算法2。
5.3.1实际应用
(1)Gim li的10轮不可能差分区分器。对于Gim li算法,之前最长的不可能差分路径是由谭豪等人[12]提出的,利用AND,OR操作的差分传播性质找到了7 轮不可能差分区分器。在5.1 节构建关于Gim li算法不可能差分区分器新型搜索模型,考虑输入差分和输出差分汉明重量均为1的情况,最终搜索到464条10轮Gim li的不可能差分区分器,这里以5.1节列出的路径为例,使用算法2进行验证。

算法2 新验证算法
由图4可知,在第5轮输出的{α108,α126}位置找到2个矛盾点。此时,模型有解当且仅当集合T1取{α108=1,α126=1},集 合T2取{β108=0,β126=0}。这意味着T1与T2不存在交集,不可能差分区分器验证成功。
(2)Xoodoo的4轮不可能差分区分器。经过验证,在第2轮输出(第3轮输入)位置找到矛盾点{α69,α78,α257,α280,α290,α313},此时集合T1取{α18=1,α27=1,α295=1,α318=1,α328=1,α351=1},集合T2取{β18=0,β27=0,β295=0,β318=0,β328=0,β351=0}。T1与T2不存在交集,4轮Xoodoo的不可能差分区分器验证成功,具体结果对比见表4。
6 结束语
本文给出了G im li/Xoodoo密码算法非线性操作与S盒之间的等价表示,构建了相应的M ILP模型来描述两个算法的不可能差分传播路径。利用自动化分析工具,对Gim li/Xoodoo密码算法抵抗不可能差分分析的能力进行了评估,发现了Gim li的10轮不可能差分区分器,相比Tan等人的结果,本文的区分器提高了3轮。Xoodoo密码算法差分类分析方面,最优差分区分器目前只搜索到3轮,本文发现了4轮Xoodoo的不可能差分区分器。进一步,为了验证区分器的正确性,利用“二分法”设计了一种新的验证算法,提高了验证效率,大大缩短了验证时间,为以后的分组密码算法的设计与分析提供了强有力的支撑。
