基于事件触发的通信有效联邦学习算法

高慧敏 杨 磊 朱军龙 张明川 吴庆涛*

①(河南科技大学信息工程学院 洛阳 471023)

②(中信重工机械股份有限公司信息技术管理中心 洛阳 471003)

1 引言

随着移动互联网和物联网的快速发展，越来越多的数据由网络中的边缘设备产生和存储。利用机器学习技术，这些分散的数据集通常被用于模型训练，但这种集中式训练方式在将物联网设备产生的数据传输到云端或者中心服务器的过程中面临着诸多挑战，例如能量和带宽限制，通信效率和隐私问题等。为解决上述问题，2016年谷歌学者提出了一个新的机器学习范式，即联邦学习[1]，它联合多个用户在云或中心服务器的协调下训练一个预测模型，同时用户之间不用交换数据，这在一定程度上保护了用户数据的隐私性。不同于去中心化的多节点协作学习[2]，联邦学习与分布式学习中的参数服务器具有相同的架构，但是联邦学习中的用户对本地数据具有绝对的自治权限，可以自主决定是否参与和退出模型训练，而且数据之间可能有着不同的分布。此外，分布式学习一般在数据中心进行并行训练，通信代价相对较小。而联邦学习中的边缘设备一般依赖互联网，其通信代价会更高[3]。面对这些新的问题，联邦学习提供了一个有效的解决方案，并被广泛应用到不同的领域，例如移动边缘网络[4]、健康医疗[5]和智能交通系统[6]等。

通信开销不仅是联邦学习的一个研究热点，同时也是一个亟待解决的问题。在每一轮的模型训练中，云端或中心服务器将当前的全局模型下发给参与训练的客户端；之后，这些客户端在本地执行多步随机梯度下降后生成本地模型；最后再将本地模型发送到云端或中心服务器。其中，通信开销主要是由客户端和云端或中心服务器之间经过网络连接传输模型参数产生。在实际场景中，随着网络中终端设备的增多、模型参数维度的增大，客户端向中心服务器发送信息时会遭受严重的网络时延和有限带宽的限制。

为了缓解客户端和云端或中心服务器之间的通信压力，减少传输的比特数是一个有效的方法，并由此延伸出许多新的压缩方法，例如通过稀疏[7]或者量化[8,9]梯度更新或者模型更新，或者将二者结合[10]使用。这类方法在保证一定模型精确度的基础上，减少了客户端之间的通信成本，因而在具有高维模型参数的深度学习领域有着广泛的应用。Li等人[11]提出加速压缩梯度下降算法，加快模型收敛的同时，节约了通信开销。分别针对同构和异构数据，Haddadpour等人[12]研究了一类通信有效的优化算法，并引入了梯度追踪方案减少客户端之间由于数据异构而产生的残差，该方法得到了更好的通信复杂度和更精确的收敛速率。

上述方法只考虑在每轮通信中减少传输的信息量，而通信的次数并没有改变。在实际训练中，连续发送的模型之间可能并没有较大的变化，这样频繁的通信是一种资源的浪费。近年来，在多智能体系统，研究人员利用事件触发机制[13,14]减少智能体之间不必要的通信，缓解网络中的通信压力。其中，如何设计触发机制是关键，以保证算法能够收敛，并达到减少通信开销的目的。Hsieh等人[15]利用梯度衡量更新的重要性，进而消除不重要的通信，其阈值设置为迭代次数平方根的倒数。文献[14]利用模型参数之间的差异确定节点的触发时刻，不同于分段参数的阈值调度方案[16]，其阈值与学习率和神经网络参数的数量有关。

为了降低联邦学习中客户端和中心服务器之间的通信代价，本文引入事件触发的通信机制，当连续更新的本地模型之间变化较大时，客户端的通信行为受到触发并将模型差异压缩后发送给中心服务器，中心服务器将收到的信息聚合后执行新一轮全局模型更新。分别在不同目标函数特征条件下，本文证明了所提方法(Federated learning w ith Event-T riggered comm unication,FedET)的收敛性，并给出了相应的理论分析。最后通过仿真实验验证了所提方法的可行性和有效性。

2 系统模型

2.1 联邦学习

在以数据为驱动的机器学习特别是深度学习中，分散的数据被收集到云端或数据中心进行模型训练。在这个过程中，数据的传输不仅受到不同网络环境特别是有限带宽的制约，而且面临着隐私泄露和被恶意篡改的风险。为了解决上述问题，基于数据不出本地，联邦学习联合多个用户学习一个共享模型，进而在网络边缘实现分布式机器学习。本文考虑由一个中心服务器和n个客户端组成的系统模型，每个客户端i拥有自己的本地数据Di，其中{1,2,...,n}表示客户端的集合，如图1所示，中心服务器给每个客户端分发当前的全局模型。在此基础上，客户端通过执行多步随机梯度下降生成本地模型，并将其上传到中心服务器。然后，中心服务器聚合所有客户端上传的模型参数，更新产生下一轮的全局模型。在中心服务器的协调下，重复以上过程，这些客户端通过协作方式解决以下有限和形式的优化问题

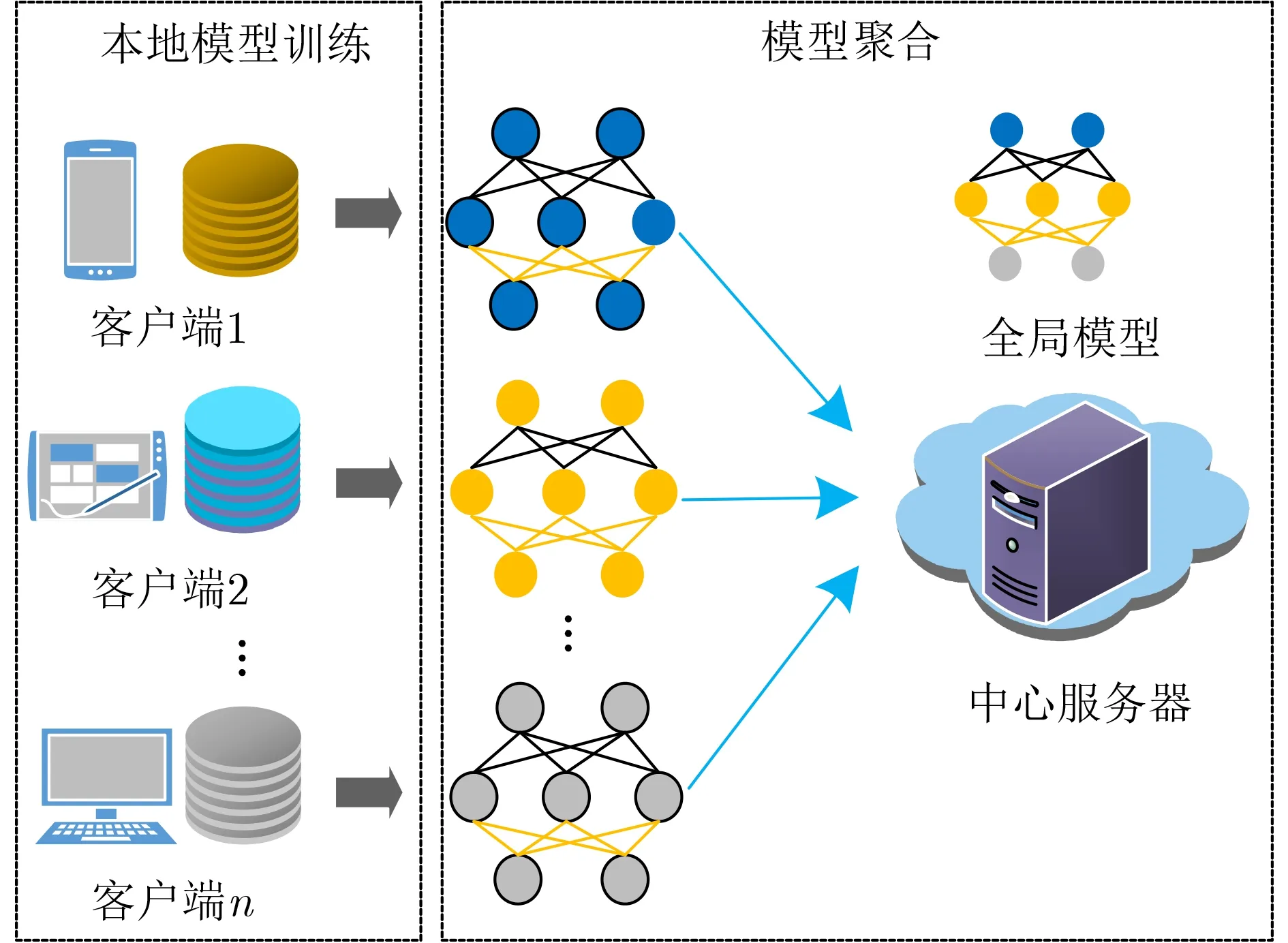
图1 联邦学习的系统架构

其中，向量x表示维度是d的模型参数，f i:Rd→R为局部代价函数，通常定义为第i个 客户端上数据样本的期望损失，表示为：fi(x)=Ez～P i[L i(x,z)]，这里L i是关于z的样本损失函数，它评估给定模型参数x的性能好坏，其中z是服从概率分布为Pi的随机变量，i∈{1,2,...,n}。一般来说，当Pi=P j时，称客户端i和j之间的数据是独立同分布的。当P i=P j时，称客户端i和j之间的数据是非独立同分布或者异质的。

2.2 符号说明

本文用 Rd表示d维实向量空间。‖·‖表示欧氏范数，‖·‖1表 示ℓ1范数。gi表示第i个客户端在模型参数x处的全梯度∇f(x,D i)，简写为∇f i(x)。表示第i个客户端在模型参数x处的随机梯度∇f(x,ξi)，其中ξi⊆D i是采样的最小批数据样本。分别表示第i个 客户端在模型参数处的梯度和随机梯度估计，其中k表示全局模型的迭代次数，h是本地模型的迭代次数。E [·]表示条件期望。

3 通信有效的联邦学习算法的设计

3.1 基于事件触发的算法设计

考虑到网络中有限带宽的限制，本节提出Fed-ET算法解决式(1)中的优化问题。该算法是一个通信有效的联邦学习算法，它利用事件触发的通信策略，结合压缩技术，减小客户端和中心服务器之间的通信负担。

为了减少客户端与中心服务器之间的通信，每个客户端i∈{1,2,...,n}需要维持本地更新xi的一个估计，并根据事件触发机制将信息压缩后上传至中心服务器。假定所提出的算法运行K次全局模型更新，也即客户端和中心服务器总的通信轮数。由于联邦学习中客户端的模型聚合是在同步环境下进行的，定义模型参数的聚合时刻集合为{0,τ,...,Kτ}，与文献[8,12]中设定类似，τ表示每个客户端本地模型更新的次数。此外，由于采样是在固定次数的局部迭代之后进行的，可知采样周期是离散的，而且文中给出至少τ倍采样周期的事件间隔的下界，因此Zeno现象在本文的设置中不会出现。

FedET算法的伪代码如算法1所示。在有中心的联邦学习架构中，首先中心服务器将全局模型的初始值x0下发给每个客户端，设置，允许每个客户端在第1轮和中心服务器通信。第k次更新时，每个客户端i通过随机采样本地数据计算梯度估计值，然后本地模型参数基于随机梯度下降进行τ次迭代得到参数向量，如算法1中第(4)～(6)行所示。在完成该轮次的本地计算之后，利用事件触发机制，每个客户端计算当前模型和最近一次发送的模型之间的差异ei(k)，定义为

其中，η是客户端的本地学习率，，k ∈，其中=0，集合表示第i个客户端触发时刻的集合。如果满足触发条件，则客户端发送压缩后的模型差异给中心服务器，并更新本地模型的估计，如算法1中第(9)和(10)行所示。否则客户端i和中心服务器在本轮不进行通信。最后，中心服务器按照下式更新下一轮的全局模型，

其中，γ是中心服务器上的学习率，C(·)是随机压缩算子。

3.2 相关假设

为了进一步分析算法的性能，首先介绍函数光滑性和随机梯度假设[17]及本文要用到的假设条件。

假设1对于代价函数f i(·):Rd →R，如果存在常数L＞0，对任意的向量x1,x2∈Rd，不等式

成立，则称函数f i(·)满 足利普希茨条件，常数L被称为利普希茨常数。本文假设f*是函数f(x)的最优值。

假设2对于每一个i∈{1,2,...,n}，参数σ＞0，随机梯度，若式(5)成立，

假设3对于随机压缩算子C(·)，参数ω＞0。对于输入向量u∈Rd，若式(6)成立，

则称随机压缩算子C(·)是无偏的，其方差随着输入向量范数的平方而变化。

假设4对于函数f(x)，参数µ＞0，如果对任意的x∈Rd，不等式成立，则称函数f(x)满足PL(Polyak-Łojasiew icz)条件。

事实上，根据文献[18]可知，任意µ-强凸函数都满足PL条件。

假设5对于函数f(x)，参数µ＞0，对任意的x,y ∈Rd，如果不等式

成立，则称函数f(x)是µ-强凸的。

假设6对于序列{αk}，假设αk=m0/(k+1)δ，其中m0＞0是参数，δ≥1/4。

假设2是关于随机梯度的常见假设。假设3是采用压缩方法的文献[8,11]中常用的条件。假设6中的δ在不同的目标函数下取值范围不同，注1给出了说明。本文的结果都是在假设它们成立的前提下得到的。

4 主要结果

本节给出以下3个主要结论，其详细证明见第5节。首先针对非凸的目标函数，当本地学习率η和全局学习率γ满足一定的条件，利用函数的光滑性，下面的定理给出了算法的收敛性。

定理1如果假设1—假设3、假设6均成立，学习率γ和η满足

则K次迭代后，梯度范数平方的平均值有界，且满足

其中，f*≜f(x*)是 函数在最优点x*处的函数值，x0是模型参数的初始值，M0表示

下面定理主要对满足PL条件的函数进行分析，而任意µ-强凸函数都满足PL条件，故只需分析满足PL条件的函数的收敛性即可。

定理2如果假设1—假设4和假设6成立，或者假设1—假设3和假设5、假设6成立，且δ＞。全局学习率γ和本地学习率η满足式(8)，则不等式(10)成立

其中，f*表示最优值f(x*)，x0是模型参数的初始值，M0表示

5 收敛性分析

6 仿真实验

本节对所提出的基于事件触发的联邦优化算法FedET进行测试和性能评估，并通过图像多级分类任务的仿真实验与FedAvg[1]和FedPAQ[8]进行对比。仿真实验主要使用MNIST[19]和Fashion MNIST[20]这两个具有代表性的数据集。其中，MNIST是手写数字集，包含0～9 10个类别。Fashion MNIST包含10个类别服装的正面图片。每个数据集都包含60 000个训练数据和10 000个测试数据。

为了模拟真实世界中多方联合学习的场景，每次实验假设10个客户端在中心服务器的协作下联合学习。本文使用PyTorch[21]作为分布式机器学习训练库，并基于Python3来实现文中所提出的算法。实验环境是：Intel i7-7500U CPU@2.70 GHz的计算机，包含一块NV IDIA GeForce 940MX GPU。针对MNIST数据集和Fashion MNIST数据集，本文使用卷积神经网络CNN作为训练模型，该模型包含两个卷积层、两个最大池化层、1个全连接层和最后的softmax输出层，使用ReLU作为激活函数。

实验假设所有客户端使用相同的网络模型，客户端之间的数据均衡且服从独立同分布：数据被随机打乱之后，每个客户端获得6000个训练样本。每个客户端通过本地数据来训练神经网络模型，也就是权和偏置，初始学习率设定为0.01，数据最小批大小为64，本地迭代次数为5。实验采用文献[8]中的压缩方法，将模型从32位浮点量化为8位整数。阈值选取方法和文献[14]中相同，阈值m0=v0N p，v0是参数，通过选择不同的v0可以改变m0的大小，N p表示神经网络模型参数总的个数。为了深入理解阈值对算法性能的影响，这里分别选取3个不同的阈值进行实验，阈值T1,T2,T3分别为0.00005Np,0.00009Np,0.00018Np。

图2是MNIST数据集上的实验结果。从图2(a)观察到，在训练前期，对于较小的阈值T1，其损失曲线(蓝色)波动较大，这是由于客户端和中心服务之间频繁的通信引起的。同理，对于较大的阈值T3，客户端和中心服务器之间信息交流相对较少，其训练损失曲线(红色)波动较小。阈值T2的训练损失曲线位于二者之间，在训练后期，虽然不同阈值情况下训练损失曲线最后均趋于稳定，但是从测试精度和迭代次数关系图2(b)不难看出，相对于较小的阈值T1和较大的阈值T3，阈值T2下的模型具有更高的精度值。从图2(c)通信开销角度来说，当客户端与中心服务器信息交流较少时，虽然通信开销较少，但是无法达到理想的精度；客户端与中心服务器之间充分交流虽然能保证精度，但是会造成大量的通信开销；适当的信息传输，如阈值T2情况下，可以以较少的通信代价最大程度的提高精度。总的来说，阈值较小时，需要昂贵的通信代价来换取算法的精度，而阈值较大时，通信开销减小，但算法精度又较差。因此，选择合适的阈值才能达到精度和通信之间最好的权衡。

图2 不同阈值对算法性能的影响

为了证明基于事件触发的联邦优化算法的优势，以下实验对比了不同算法下的收敛速度、平均通信开销和测试精度，包括联邦平均Fed Avg和FedPAQ算法。图3分别刻画了在不同数据集上全局模型的平均训练损失和迭代轮次之间的关系，其中图3(a)是在MNIST数据集上的运行结果，可以看出FedET算法达到了和FedAvg和FedPAQ算法相似的收敛速度，虽然模型变化不大时客户端和中心服务器不进行通信，但独立同分布的数据特征使算法快速收敛。在Fashion MNIST数据集上有类似的结果，如图3(b)所示。

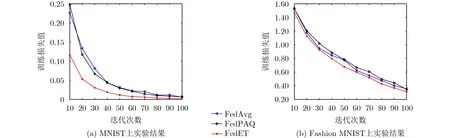
图3 训练损失和迭代次数之间的关系

图4显示了客户端和中心服务器之间上行链路中平均累计通信开销和训练损失值的变化关系。从图4(a)可以观察到，当达到最小损失时，FedAvg的通信比特数最多，FedPAQ次之，FedET的通信代价最少。这是由于算法分别采取了不同的通信有效技术引起的。FedAvg算法中客户端向中心服务器发送整个模型参数，FedPAQ算法将模型之间的差异压缩后上传给中心服务器，而FedET使用压缩和事件触发机制，和前两个算法相比分别节约了64%和10%左右的通信。在Fashion MNIST数据集上的实验结果如图4(b)所示，当达到0.2的训练损失值时，FedET分别比FedAvg,FedPAQ节约了75%和35%左右的通信量。

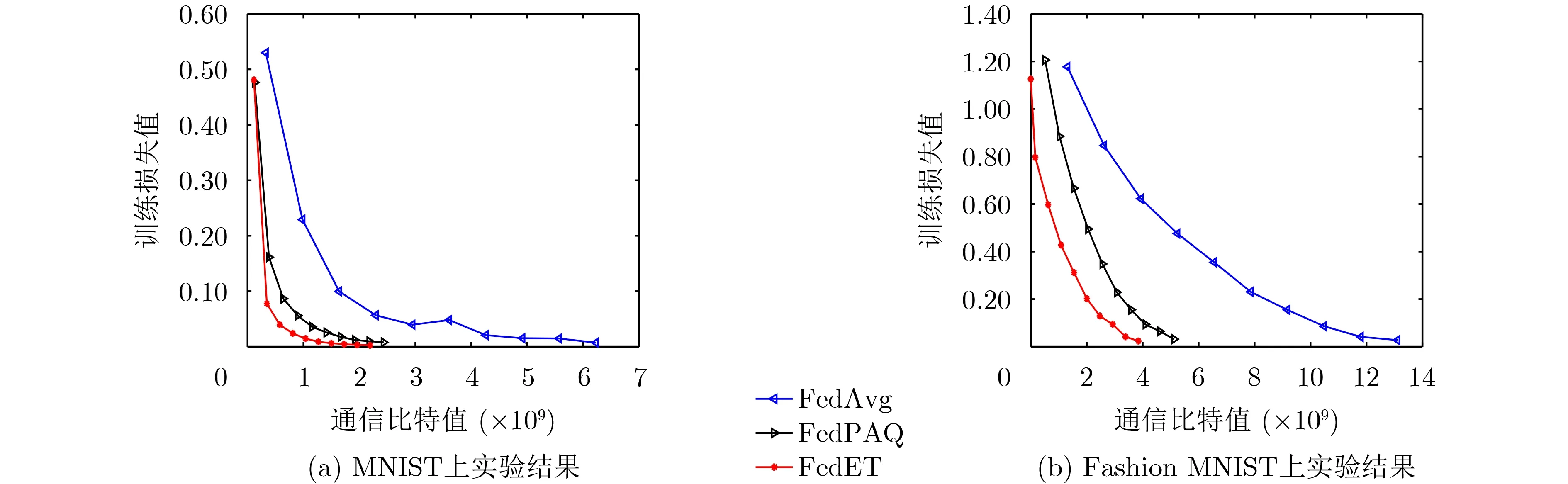
图4 训练损失和通信量之间的关系

测试精度是衡量模型泛化性能的一个重要指标。图5刻画了测试集上全局模型的预测精度在平均累计通信开销下的变化趋势。从MNIST数据集上的实验结果图5(a)不难看出，当达到大约99%的精度时，Fed ET使用最少的通信比特值，Fash ion MNIST数据集上的实验结果和上述结论是类似的，如图5(b)所示。在资源有限的网络环境下，事件触发机制的使用降低了对通信带宽的需求。两个数据集上的实验结果验证了本文所提的联邦优化算法FedET的可行性和有效性。

7 结束语

本文基于事件触发机制提出一个通信有效的联邦优化算法，用于解决联邦学习中的通信开销问题。该算法通过减少上行链路中客户端到中心服务器不必要的信息传输，同时结合信息压缩技术减少每轮发送的信息比特数，缓解联邦学习中的通信瓶颈。在客户端数据独立同分布时，针对不同的目标函数特征，本文从理论上分析了所提算法的收敛性，并给出了相应的数学证明。最后，在MNIST和Fashion MNIST这两个公共数据集上执行仿真实验，结果表明，所提算法能在合适的阈值下达到与FedAvg和FedPAQ算法相似的精度，同时节约了通信成本。