基于合作博弈和知识蒸馏的个性化联邦学习算法
2023-11-18孙艳华史亚会杨睿哲司鹏搏
孙艳华史亚会 李 萌 杨睿哲 司鹏搏
(北京工业大学信息学部 北京 100124)(北京工业大学先进信息网络北京实验室 北京 100124)
1 引言
联邦学习(Federated Learning,FL)是一种去中心化、保护数据隐私的分布式机器学习[1],由中心服务器调控,多个客户端相互协作共同训练得到一个共享模型,并且不需要直接访问客户端的私有数据,从而在一定程度上避免了隐私泄露。
但是FL的有效实现很大程度上依赖于客户端之间相似的数据分布以及完全相同的模型架构,而在绝大多数实际场景中客户端数据往往是非独立同分布(Non-Independent Identically Distributed,Non-IID)的[2],这导致FL训练的共享模型不能满足每一个客户端的需求。另外,在医疗保健、人工智能等领域,每个客户端需独立设计模型来满足自身的需求。而个性化联邦学习(Personalized Federated Learning,PFL)则充分考虑了FL的异构性影响。
为了解决FL中客户端隐私数据Non-IID的问题,文献[3]提出了一种联邦迁移学习方法,将本地模型视为“基础层+个性化层”,基础层负责共享,个性化层进行本地训练。文献[4]则混合本地模型和全局模型,采用正则函数在两种模型之间找到一个折中,从而提高本地精度。文献[5]利用元学习找到一个初始的共享模型,使客户端能只进行1步或者几步梯度下降便能快速适应本地数据集。文献[6]在每次全局迭代中确定聚类簇,并在簇内进行个性化训练来提高客户端的个性化精度。文献[7]在客户端隐私数据集上用夏普利值来衡量客户端数据相似度并进行FL。然而上述方法仅针对客户端数据Non-IID问题,且需要客户端模型结构和大小相同。
受知识蒸馏(Know ledge Distillation,KD)可以通过交换软预测而不是整个模型参数来将知识从一个神经网络转移到另一个神经网络的思想的启发[8],文献[9]提出了联邦模型蒸馏(Federated learning w ith M odel Distillation,FedMD)算法,以保护隐私的方式协同训练异构模型。文献[10]采用集成蒸馏,在每次全局迭代中将所有异构客户端模型的知识迁移到全局模型。然而这些算法忽略了参与训练的客户端进一步的个性化需求。文献[11]提出了知识迁移个性化联邦学习(Know ledge T ransfer for personalized Federated Learning,KT-pFL)算法,将成对客户端相似度进行参数化,并采用KD将个性化软预测的知识迁移到本地。文献[12]采用集群共蒸馏将具有相似数据分布的客户端的知识迁移到本地。然而这些算法都是通过成对客户端的相似性来进行个性化知识迁移的,而最近一些研究发现模型聚合本质上是一种合作博弈[13],客户端之间的影响是多重的,仅仅依靠1对1的模型相似性来衡量客户端之间数据以及模型的相似度并确定模型聚合系数的方法往往忽略了这一点。
综上所述,目前大多数的个性化联邦学习研究都建立在同构模型的基础上,或者只考虑了成对客户端协作时的相似度。本文提出的基于合作博弈和知识蒸馏的个性化联邦学习(personalized Federated learning w ith Collation gam e and Knowledge distillation,pFedCK)算法不仅打破了FL中客户端数据独立同分布和模型架构相同的局限,而且利用合作博弈论中的夏普利值(Shap ley Value,SV)[14]来评估合作联盟中的每个客户对其他客户端的个性化学习过程的累计贡献值,并以此确定联盟中每个客户端局部软预测的聚合系数,最后利用KD将聚合的个性化软预测的知识迁移到本地模型,并在本地的隐私数据集上进行个性化训练,提高个性化精度。
2 相关工作
2.1 合作博弈
博弈论既可以用来竞争也可以用来合作,并据此可以分为合作博弈和非合作博弈,其中合作博弈是指参与者以同盟、合作的方式进行不同联盟之间的对抗,关注的是达成合作时如何分配合作得到的收益[15]。
合作博弈中的SV用来计算累计贡献的均值,是一种分配方式,往往贡献越大,收益就相对越多。将SV引入PFL可以通过分析联盟聚合时的多重影响来评估每个客户端对其他客户端个性化学习的累计贡献。FL中的每个客户端相当于合作博弈中的一个玩家,其中N={1,2,...,n}为所有客户端的集合,C为集合N的任意子集,可用来表示一个联盟,v(C)为 联盟C中所有元素合作产生的整体效益,一般定义v(∅)=0,采用SV可以将联盟的整体效益进行分配,收益φj(v)(j ∈C)表示客户端j在集合N的所有子集中产生的贡献的累计均值
2.2 知识蒸馏
知识蒸馏是一种基于“教师-学生”思想的模型压缩方法,一般用于将复杂模型的知识压缩到较为简单的模型中。通常先训练好一个教师网络,然后将教师网络的输出结果作为学生网络学习的目标,从而训练学生网络使其输出不断接近教师网络。因此KD损失包含两部分,一部分为软损失,另一部分为本地训练损失。
然而在软损失中,直接使用教师网络中softmax层的输出结果会过滤掉大量的有用信息,因此一般采用温度参数T(T >0)来平滑各个类别对应的概率分布,softmax函数就是T=1时的特例,T的值越大,softmax层的输出概率分布就越趋于平滑,负标签携带的信息会被相对地放大
其中,x表 示学生网络的数据集,Mstu表示学生模型,Mtea表示教师模型,并且采用KL(Ku llback-Leible)散度衡量两个模型之间的差距。则KD的总损失可以表示为
其中,λ∈(0,1)为加权系数,用于控制学生学习教师的程度,Lcro为交叉熵损失函数,y是学生端数据的标签。
3 基于合作博弈和知识蒸馏的个性化联邦学习算法
3.1 训练目标
本文的训练目标在于为一组在FL中数据Non-IID并且模型架构不同的客户端协作训练个性化模型。假设客户端N={1,2,...,n},每个客户端i只能访问隐私数据集D i。在传统的FL中,学习目标为得到一个全局模型ω使所有客户端的总经验损失最小
其中,L i(ω,D i)是客户端i的本地损失函数。然而式(4)要求所有客户端有统一的模型架构,且在本地数据Non-IID时训练效果明显下降。因此本文在此基础上将客户端i的本地损失函数定义为
其中,Dp表示公共数据集,每个参与训练的客户端均可访问,为经过合作博弈后聚合得到的客户端i的个性化软预测,l ogiti为客户端i的局部软预测,进而pFedCK算法的训练目标可以表示为
3.2 pFedCK算法
pFedCK算法的具体过程如算法1所示。
迁移学习:为避免客户端私有数据稀缺对训练结果造成影响,在FL训练之前,采用迁移学习使客户端先在Dp上 训练至收敛,然后在Di上进行微调。
然后根据SV将合作联盟的整体效益分配给联盟中的每个客户,表示它在的所有子集X中对当前客户端i个性化学习的贡献的累计均值
然后将下载的k个软预测以及客户端i的局部软预测进行聚合得到个性化软预测
其中,p,q分别为客户端i的本地软预测和聚合的个性化软预测的比例系数。
其中,ωi为客户端i的模型参数,η1,η2为学习率,L i(ω,D i)则 为客户端i在隐私数据集Di上 的损失函数。
4 实验仿真
4.1 仿真设置
实验基于Tensorflow进行,并与FedMD算法、首k联邦学习(Top k-Federated Learning,Topk-FL)算法以及KT-pFed算法进行比较,其中Topk-FL算法仅根据余弦相似度从服务器端下载k个软预测进行平均,进而在本地进行学习。所有算法的性能都通过所有客户端的平均测试精度来评估。
数据集:在两种数据场景下进行实验。
(1)公共数据集是国家技术与标准混合研究所(M ixed National Institute of Standards and Technology,MN IST)数据集,隐私数据集是扩展MN IST(anExtension of MNIST,EMNIST)数据集。对于隐私数据集采用IID和两种Non-IID情况,在Non-IID 1中,每个客户端只有EMNIST中一类作者的字,且样本数量相同,在Non-IID 2中每个客户端有EMNIST中所有作者的字,但是样本总量不同。两种情况下都要求在测试时对所有作者的字进行分类。

算法1 pFedCK算法
(2)公共数据集是CIFAR 10,隐私数据集是CIFAR100。CIAR100数据集有20个超类,每个超类包含5个子类,每个类有600张大小为32× 32的彩色图像。同样地,对于隐私数据集同样采用IID和两种Non-IID情况,在Non-IID 1中,训练时每个客户端只包含1个大类中的1个子类,且样本数量相同,在Non-IID 2中每个客户端包含所有的类,但是每个类的样本数不同,即每个客户端的样本总数不同,两种情况下测试时都需要将通用的测试数据集分类为正确的大类。
模型架构:实验采用了3种不同的模型结构,包括2层卷积神经网络,3层卷积神经网络以及A lexNet,并将这3种模型分配给10个客户端,每个客户端的模型参数均不同。
实验细节:本文设置全局迭代20次,本地迭代20次,本地蒸馏3次,且每次全局迭代中客户端根据余弦相似度下载7个软预测(即k=7),学习率η1,η2均为0.001,公共数据集为5000,p-q为0.3–0.7,λ为0.5,其余参数均按照各个算法的最优设置。
4.2 仿真结果
本节展示了p Fed CK算法与FedM D算法、Topk-FL算法以及KT-p Fed算法的训练效果比较,并对实验结果进行了详细分析。
表1总结了4种算法的训练精度。在表1中,pFedCK算法能在隐私数据IID的情况下,将个性化精度在KT-p Fed算法的基础上提高约7%,且在Topk-FL算法的基础上提高约8%,在FedMD算法的基础上提高约15%;在隐私数据集Non-IID 1的情况下,将个性化精度在KT-pFed算法的基础上提高约3%,在Topk-FL算法的基础上提高约5%,在FedMD算法的基础上提高约10%;在隐私数据集Non-IID 2的情况下将个性化精度在KT-p Fed算法的基础上提高约2%,在Topk-FL算法的基础上提高约4%,在FedMD算法的基础上提高约8%。这是因为FedMD算法没有考虑不同客户端的个性化需求,TopK-FL算法没有考虑客户端之间相互协作的影响,KT-pFed算法只根据成对客户端的相似性来决定其参数矩阵中的值并进行个性化,而本文的pFedCK算法则采用合作博弈的思想考虑到了客户端模型聚合时的多重影响,以此确定聚合系数来提高个性化。

表1 4种算法在不同数据集下的个性化精度
图1和图2分别展示了4种算法中10个客户端在不同数据集训练过程中的平均训练精度曲线。由图1可知,EMNIST数据集IID时pFedCK算法的训练精度能在其他3种算法的基础上实现较高程度的提升,且训练速度明显快于其他3种,而KT-pFed算法与Topk-FL算法的训练速度以及精度提升效果基本相当,均明显逊色于pFedCK算法,FedMD算法则会在第10次全局迭代左右出现较明显的浮动,相对不稳定。隐私数据Non-IID1时,客户端数据异构,训练难度增大,pFedCK算法的训练精度同样明显优于其他3种算法。TopK-FL算法的训练速度较快,在训练后半程训练精度和KT-pFed算法精度水平基本相当,而FedMD算法的训练精度则最低。隐私数据Non-IID2时,数据异构程度进一步提高,4种算法的训练精度都有所下降,此时pFedCK算法相对于其他3种算法依然有较明显的提升,而KT-pFed算法和Top-KL算法相对于FedMD算法的提升效果则相对较差。
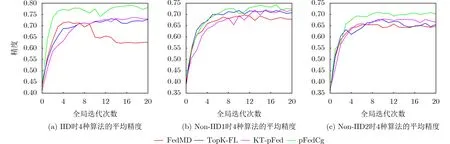
图1 MNIST-EMNIST中4种算法的平均精度

图2 CIFAR10-CIFAR100中4种算法的平均精度
由图2可知,由于CIFAR10-CIFAR100的数据复杂度相对较高,这种场景下4种算法实现的数据精度均低于MNIST-EMNIST数据场景,且浮动较大,较为频繁。CIFAR100数据集IID时,pFedCK算法训练最快,且训练精度相对于其他3种算法能实现明显的提升,而KT-pFed算法和Topk-FL算法的训练精度的提升幅度较低,且训练速度基本与FedMD算法持平,FedMD算法的训练精度则最低。CIFAR100数据集Non-IID1时,由于本地数据分布异构,训练过程中4种算法均出现较为频繁的浮动,但pFedCK算法仍然能实现较快的训练速度以及最大幅度精度提升,而KT-pFed算法的训练速度较快,训练效果与Topk-FL算法基本持平且相对较差。CIFAR 100数据集Non-IID 2时,4种算法的训练精度均进一步降低,此时Topk-FL算法的训练效果提升幅度相对较差,KT-pFed算法在训练后半段出现较明显的提升,而pFedCK算法此时仍然比其他3种算法的训练精度要高,并且训练稳定性也较好。
综上所述,客户端模型异构时,pFedCK算法在不同数据集以及不同数据分布下均能获得在同样设置下优于其他算法的效果。
4.3 超参数的影响
为了了解不同的训练参数对pFedCK算法效果的影响,本文在学习率η1,η2均为0.001的情况下在两种不同的数据场景下进行了各种实验。
本地迭代次数:表2展示了不同本地迭代次数下pFedCK算法的平均精度。可以看出,在MNISTEMNIST数据场景下,隐私数据IID时本地迭代次数为10的时候个性化精度最高,隐私数据Non-IID1和Non-IID2时本地迭代次数为20的时候个性化精度最高。在CIFAR10-CIFAR100场景下,隐私数据IID时本地迭代次数为15的时候个性化精度最高,隐私数据Non-IID1和Non-IID 2时本地迭代次数为20的时候精度最高。可以看出,数据复杂程度越高,在本地训练的次数也越多。
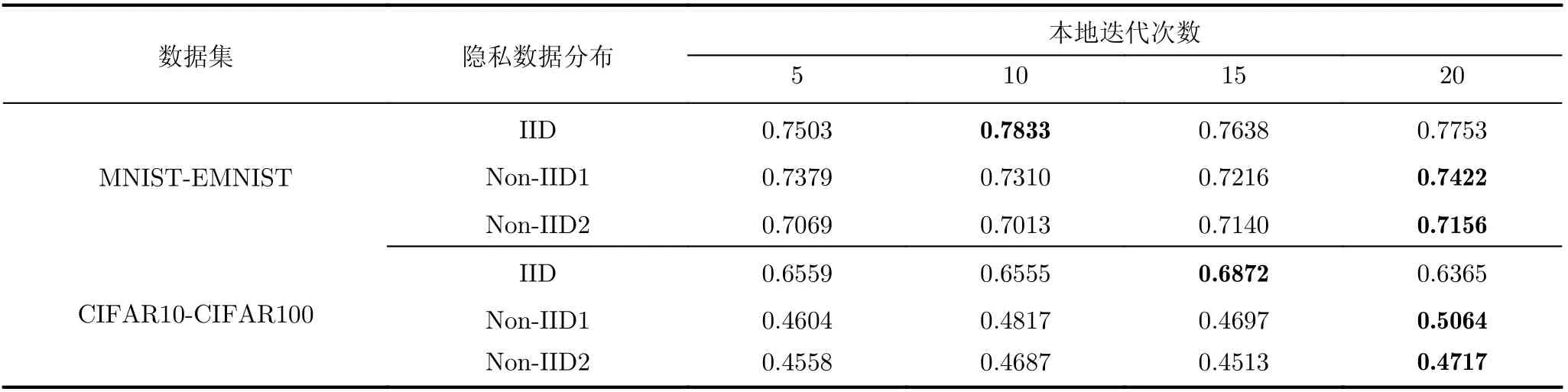
表2 不同本地迭代次数下pFedCK算法的个性化精度
本地蒸馏次数:表3展示了不同本地蒸馏次数下pFedCK算法的平均精度。可以看出,在MNISTEMNIST场景下,隐私数据IID时本地蒸馏次数为5的时候个性化精度最高,隐私数据Non-IID 1和Non-IID 2时本地蒸馏次数为3时个性化精度最高。在CIFAR10-CIFAR100数据场景下,隐私数据IID时本地蒸馏次数为3时个性化精度最高,而隐私数据Non-IID1和Non-IID2时本地蒸馏次数为2时个性化精度最高。由此可知数据复杂程度越高时,本地蒸馏次数越低,越有利于本地个性化训练。
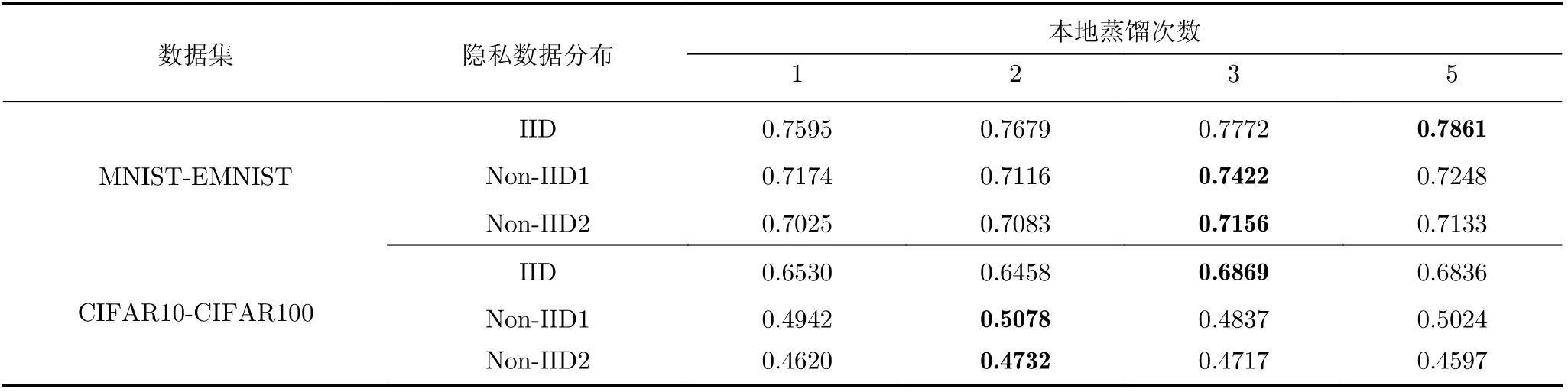
表3 不同本地蒸馏次数下pFedCK算法的个性化精度
p,q:表4展示了不同p,q下pFedCK算法的平均精度变化。可以看出在MNIST-EMNIST数据场景下,隐私数据IID时p,q为0.1,0.9时个性化精度最高,隐私数据Non-IID1时p,q为0.4,0.6时个性化精度最高,隐私数据Non-IID2时p,q为0.3,0.7时个性化精度最高。而在CIFAR10-CIFAR100数据场景下,隐私数据IID,Non-IID1时p,q为0.3,0.7时个性化精度最高,隐私数据Non-IID 2时p,q为0.4,0.6时个性化精度最高。由此不难发现,本地数据复杂程度越高时,往往本地软预测所占的比例越高,越有助于本地客户端的个性化训练。

表4 不同p-q下pFedCK算法的个性化精度
加权系数λ:表5展示了不同加权系数λ下pFedCK算法的平均精度的变化,可以看出在MNIST-EMNIST数据场景下,隐私数据IID时λ为0.1时效果最好,隐私数据Non-IID 1和Non-IID 2时λ等于0.3时效果最好,而在CIFAR10-CIFAR100数据场景下,隐私数据IID时在λ为0.5时效果最好,隐私数据Non-IID 1和Non-IID 2时λ为0.8时效果最好。由此可以看出数据复杂程度越高时,要学习的知识更多,因此往往在知识蒸馏过程中教师模型所占据的比重更大。
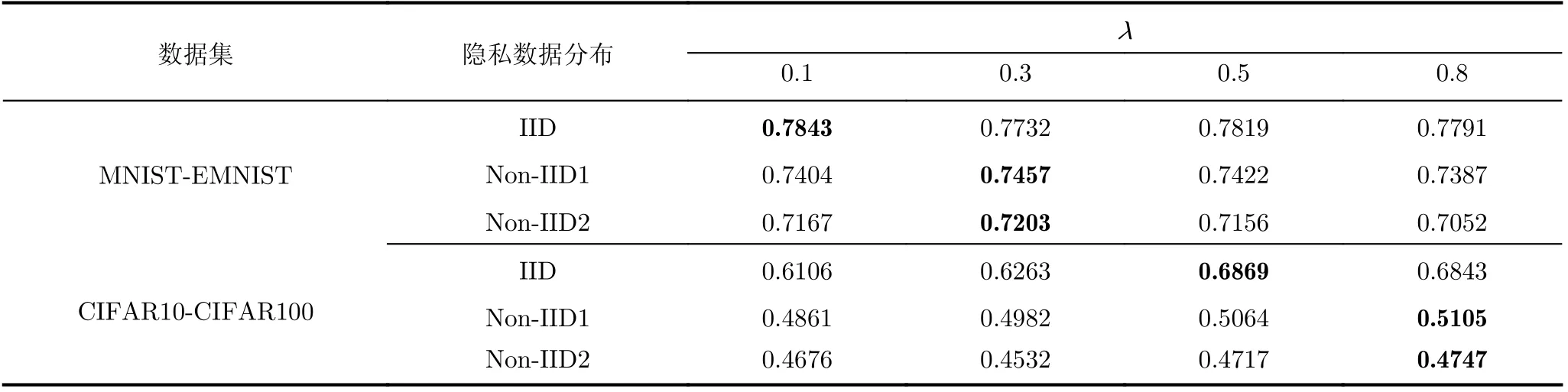
表5 不同λ下pFedCK算法的个性化精度
综上所述,对于客户端本地数据的不同异构情况,数据异构程度越高时,为了获得更好的训练效果,往往需要本地迭代次数相对较多,本地蒸馏次数相对较少,并且p,q的比例相对较大,λ的值也相对较大。
5 结束语
针对FL中客户端数据异构时影响训练速度以及训练精度,客户端模型异构无法进行训练的问题,本文提出了基于合作博弈和知识蒸馏的pFedCK算法,将合作博弈论中的SV引入到个性化联邦学习中,以分析客户端之间协作时的多重影响,并且将其对其他客户端个性化的累计贡献以平均值的形式量化,进行个性化聚合,然后在本地引用知识蒸馏克服模型异构的影响并将个性化软预测的知识迁移到本地。实验结果证明,pFedCK算法能明显地提高客户端的训练精度。除数据和模型异构之外,FL还存在系统异构性问题,如本地资源,通信能耗等,下一步研究工作将综合考虑解决两种异构性问题。
