核心素养背景下数形结合思想在小学数学解题中的应用研究

2023-11-18李亚密

名师在线 2023年29期

文/李亚密

《义务教育数学课程标准（2022 年版）》提出了许多先进的课程观念和教学理念，倡导教师在实际教学中引导学生感悟其中的数学思想，如数形结合思想，引导学生运用数学思想分析问题、解决问题，确保学生的数学综合能力得到稳步发展。基于此，教师必须转变以往以“知识教育为主”的陈旧思想，加强对学生解题能力的培养，将数形结合思想渗透到具体的教学中，让学生运用画图策略更好地解决问题，使他们的审题能力、数形转化能力、解题能力得到发展。

一、数形结合思想的基本特点

（一）“以数解形”的特点

1.借助“数”，认识图形

将图形和数量关系进行有效融合可以帮助学生直观理解图形，提高学生解题的准确性。以“三角形的性质”为例，为了让学生进一步认识三角形，教师可以组织他们裁剪三张长度不一（如5 cm、8 cm 和17 cm）的细长纸条，将它们拼成一个三角形。这样，学生可以直观地看到这三个纸条是否可以拼成三角形，进而借助“数”来得出结论：因为5+8＜17，所以无法组成三角形。像这样通过对数量关系进行分析可以加深学生对图形特征的记忆。

2.借助“数”，精确画图

为了提高学生画图的精确性，教师可以借助数量关系引导学生准确画图。以“梯形的认识”为例，在绘制图形之前，教师要先引导学生明确梯形每条边的数量关系，如“梯形的下底要比上底长3 cm，已知上底为5 cm，请你画出下底。”结合具体的“数”来绘制图形，先画出上底（5 cm），再画出比5 cm 多3 cm 的下底，这样“以数解形”的方法可以提高学生画图的精确性[1]。

（二）“以形助数”的特点

1.借助“形”，充分认识数

通过图形的辅助，学生能更好地认识数，对数字背后的深刻含义形成全方位的认识，从而构建清晰的数字概念。以“1000 以内数的认识”为例，1000 对学生来说是大数，为了帮助学生形成“1000”的概念，教师可以让学生画出一个小正方形来表示“1 个一”，画出10 个小正方形表示“1 个十”，然后让学生结合“1个十”，想象“1 个百”“1 个千”，以此类推，使学生结合具体的图形来构建“1000”的概念，从而加深理解。

2.借助“形”，理解数量关系

在数学解题中，部分学生会因为没有深刻理解题目中的隐性条件而出现不必要的错误。对此，教师可以引导学生借助“形”来理解问题中的数量关系，让学生通过更直观的方式把题目中复杂的数量关系表现出来，这样更有助于学生理解题意，找出相应的解决思路。画线段图是学生在解题中经常用到的一种方法，教师可以鼓励学生在读完题之后绘制线段图，使他们理解题目中各种复杂的信息和数量关系，为顺利解题提供支持。

二、核心素养背景下数形结合思想在小学数学解题中的应用对策

（一）研究和利用教材中的数形结合思想

要想有效培养学生的解题能力，教师就必须对教材中蕴含的数学思想进行认真解读和分析，充分利用课本中的资源，在讲解某一课或某个章节时对学生渗透数形结合思想，使他们灵活运用这一思想来分析、解决问题。

（二）根据学生特征改进数形结合思想教学方式

1.创设教学情境，提高数形结合应用意识

教师要注重对各式各样教学情境的创设，把知识点放置于熟悉的情境中，让学生可以在生动的情境中分析、解决问题，循序渐进地掌握运用数形结合思想来解题的关键能力。这样才能促进学生高效学习，提高他们对该思想的应用意识[2]。

以“比例尺”这部分为例，教师对课本上的例题进行了改编，向学生呈现了以下题目：

阳光小学的小兰同学突发奇想，想要给学校画一幅平面图，但还没开始就遇到了一个问题，他们学校的草坪长为50 m，宽为30 m，那么这么大的草坪一张纸肯定是容不下的，应该如何才能把它画到纸上呢？小兰同学非常疑惑，你可以帮她解决吗？

在问题的驱动下，学生产生了好奇心，逐渐进入情境中，开始对比例尺的知识展开探索，最后运用比例尺的知识帮助小兰解决了问题，并绘制出了校园平面图。

2.利用信息技术，辅助数形结合思想教学

与传统口授的教学模式相比，现代信息技术的优势在于可以向学生呈现更多学习资源，通过图画、音视频的融入给学生带来视觉、听觉上的冲击，充分引起学生对当堂课所教内容的关注。对于一些学生难以理解的问题，教师可以借助直观的视频图画来展示，鼓励学生直接从中获取相关的信息。

例如，在教学“扇形统计图”这部分内容时，教师可以利用多媒体给学生展示问题中的相关数据，让学生对图形中的信息进行分析。比如，图片是关于“牛奶中的营养成分”的，通过观察图形，学生可以从中获取“水分是87%”“蛋白质3.3%”“乳糖5%”等多个信息。接着，教师向学生提出问题：“蛋白质、脂肪和乳糖的占比是多少呢？”这样，学生可以结合统计图快速展开计算，得到三者的营养成分占比，提高解题的效率。此外，教师通过信息技术展示图形还有利于学生进一步了解扇形统计图的特点。

（三）通过多种活动渗透数形结合思想

1.设置问题，体会数形结合价值

在解题的过程中，很少有学生运用数形结合思想来分析题目，更喜欢采取直接列式、计算的方法。当询问学生具体的原因时，他们回答自己对画图缺乏一定的兴趣，认为通过画图来解题太麻烦。这说明当前部分学生还未意识到数形结合思想在数学解题中的重要作用。因此，在具体的教学中，教师需要针对学生的问题，采取相应的手段，针对小学生的认知水平给他们设置问题，让学生对问题产生疑惑，并带着疑惑展开全方位、深层次的思考。教师可以抓住时机给学生出示图形，让学生结合图形分析题目中的信息，也可以鼓励他们尝试画图，让他们体会到图形的重要性，体会到数形结合的价值。

以“钉子板上的多边形”为例，教师先给学生出示了一幅图片（如图1），然后提出了这样一个问题：“同学们请看这些多边形，你知道它们的面积分别是多少吗？在每个多边形的边上分布了几个钉子？请你数一数，算一算。”

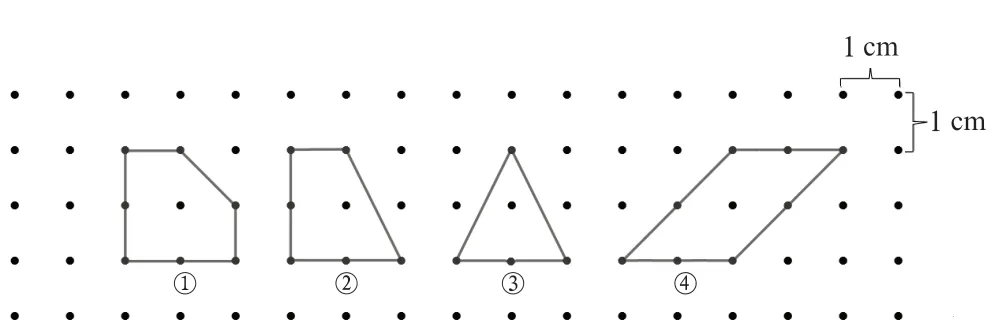
图1

在读完这个问题后，很多学生会认为这是一个“形”的问题，但是仅通过对图形的观察是难以发现其中规律的。这时，教师需要引导学生得出每个多边形的面积、多边形边上钉子的数量，并把这些信息填入表格。教师逐渐引导学生把图形问题转化为面积问题，经历“由形到数”的转化，在此基础上让学生计算验证，可充分体会数形结合的重要性。

2.科学指导，应用数形结合思想

由于受思维、认知水平的限制，很多学生对数形结合的认识还不够深刻。因此，教师应充分发挥自身的作用，在课堂上给予学生适当的指导，让学生在遇到疑难的数学问题时可以自觉运用数形结合思想来分析、解题[3]。教师要保持一定的耐心，给予学生足够的感知、探索、运用的时间，同时充分发挥自身的引导和督促作用。对于学生存在疑惑的地方，教师也可以多借助数形结合的方式进行讲解和阐释，让学生在今后的解题中自觉应用这一思想。

以工程队问题为例，在组织学生学完“简易方程”这部分内容后，教师给学生设计了这样的问题：

能量工程队平均每天要修路x米，在修了35 天之后，他们还剩下30 米没有完成，这条路的总长是1780米，如图2，请问能量工程队每天修多少米呢？

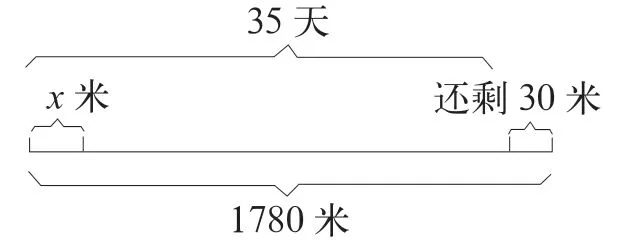
图2

学生很快就想到运用画图策略来解决这类问题。于是，他们在本子上用线段来画出对应的图，通过画图的方式开阔解题思路，自主分析数学问题并列出相应的式子。有的学生列了1780-30=35x的式子，也有的学生列出35x+30=1780 等，最后通过自己的能力解决问题。

3.鼓励学生画图，促进问题顺利解决

到了中高年级，学生的数学学习能力得到了提升，但是在面对一些比较复杂的数学问题时，如果缺少对科学方法的掌握，也会“不知所措”，甚至放弃。因此，在具体教学中，教师要向学生渗透数形结合的方法，积极鼓励学生运用画图策略来解决问题，使他们在画图、分析图的过程中找到解题的关键点，形成清晰的逻辑思维，有效地解决问题[4]。

例如，在教学五年级“鸡兔同笼”的问题时，教师引入了古代的假设法来引导学生解题。教师如果单纯地通过口头讲解的方式向学生阐明鸡、兔的变化，肯定难以激发学生数学解题的兴趣。但是教师如果采取数形结合的方式，鼓励学生在本子上画一画鸡和兔的数量，再比一比头和脚的数量，这样学生就可以更直观地理解鸡和兔两个变量，找到解题的思路与方法[5]。又如，教师向学生出示了一个问题：“某仓库有一堆纯净水，今天运走了35 吨，还余下总数的2/7 没运，请问还剩下多少吨水？”部分思维能力较弱的学生说可能一下找不到解题的思路。于是，教师鼓励他们在纸上画出线段图，这样就可以“一目了然”，掌握运走的水占据总数的多少，从而顺利解题。