2022年克鲁伦河流域土壤全氮含量与土壤全磷含量数据集

王辰怡，高秉博*，Sukhbaatar Chinzorig，冯权泷，冯爱萍，姜传亮，张中浩，及舒蕊

数据论文

2022年克鲁伦河流域土壤全氮含量与土壤全磷含量数据集

王辰怡1，高秉博1*，Sukhbaatar Chinzorig2，冯权泷1，冯爱萍3，姜传亮1，张中浩4，及舒蕊1

1.中国农业大学土地科学与技术学院，北京 100083，中国；2.蒙古科学院地理与生态地质研究所，乌兰巴托 15170，蒙古；3.生态环境部卫星环境应用中心，北京 100094，中国；4.上海师范大学环境与地理科学学院，上海 200234，中国

克鲁伦河流域生态环境安全在中蒙两国受到越来越多关注，掌握流域土壤全氮（STN）和土壤全磷（STP）含量对于准确估算流域面源污染（NPS）负荷、研究流域资源环境状况与可持续发展具有重要意义。传统采样方法在获取大范围的STN和STP含量时耗时耗力、STN与STP存在空间异质性、STN和STP与辅助变量间的关系也存在空间异质性等。单一的全局模型无法拟合复杂的异质性关系，而局部建模方法难以克服维度灾难问题，因此本文引入了两点机器学习（TPML）方法。该方法首先基于点对差异建立全局模型，然后基于全局模型的预测差异构建局部模型，能够将样本量从n扩充至n2，可利用有限的采样点数据实现高精度大范围的STN和STP含量预测。本文结合地形、气候、土壤属性、植被及空间位置等共18个辅助变量，采用TPML方法，制作了流域STN和STP含量分布数据集。并基于十折交叉验证方法证实了TPML方法相较于普通克里格（OK）方法，预测精度提高超过10%。TPML方法预测STN含量的平均绝对误差（MAE）均值和平均均方根误差（RMSE）分别为0.309%、0.456%，随机森林（RF）、反距离加权（IDW）与OK方法预测STN含量的平均MAE分别为0.329%、0.247%与1.864%，平均RMSE分别为0.468%、0.387%、1.976%。TPML方法预测STP含量的平均MAE和平均RMSE分别为0.640%和0.861%，RF、IDW与OK方法预测STP含量的平均MAE分别为0.643%、0.396%与1.357%，平均RMSE分别为0.862%、0.523%与1.651%。

克鲁伦河流域；两点机器学习；土壤全氮；土壤全磷

1 引言

克鲁伦河发源于蒙古国肯特山并最终注入我国北方第一大淡水湖——呼伦湖。近年来，呼伦湖水质污染形势严峻，严重影响区域生态安全与饮用水安全。克鲁伦河流域土壤中的氮、磷以颗粒态和溶解态的形式进入水体，成为流域面源污染（Non-point sources, NPS）的主要来源之一。因此掌握流域内土壤全氮（Soil total nitrogen, STN）、土壤全磷（Soil total phosphorus, STP）含量的空间分布对于理清NPS负荷分布模式，探究污染来源和数量至关重要。由于流域土壤全氮、全磷含量采样化验成本高、耗时长，样本量有限[1]。需要采用先进的空间预测方法估算未采样点土壤的STN和STP含量。目前，基于有限采样点数据进行STN和STP含量的空间预测已有较多研究。Shen等[2]利用反距离加权（Inverse distance weighted, IDW）、普通克里金（Ordinary kriging, OK）、多元线性回归（Multiple linear regression, MLR）、地理加权回归克里金（Geographically weighted regression kriging, GWRK）等共8种方法预测STN含量，探究了最优的预测方法。但是传统的空间预测方法往往不能充分利用目标变量和环境变量间的相关关系，无法得到精确的目标变量的局部预测结果[3-5]。

为能充分利用土壤属性与环境变量间关系建立高精度土壤属性预测模型，大量研究开始引入机器学习建模方法[6-8]。彭涛等[9]采用无人机高光谱波段和偏最小二乘回归（Partial least squares regression, PLSR）、岭回归（Ridge regression, RR）和随机森林（Random forest, RF）方法进行STN含量的预测建模，预测高精度的STN含量的空间分布。Hengl等[10]使用RF和梯度提升（Gradient boosting）机器学习技术的集合，预测非洲撒哈拉以南地区0～30 cm的STN和STP等土壤属性含量，并进行土壤数字制图。机器学习方法采用全局建模和局部建模两种方式。Gomez等[11]利用PLSR方法建立全局模型，预测突尼斯的土壤有机碳和土壤无机碳含量。但是全局模型在处理土壤属性与环境变量的局部异质性关系上存在局限性。因此局部预测模型被开发以提高预测精度，Ramirez-Lopez等[12]建立了一种预测土壤属性的局部模型，基于光谱的学习器（Spectrum-based learner, SBL），结果表明其在利用大量丰富的Vis-NIR数据集预测土壤属性含量方面具有巨大的潜力。但是随着输入局部预测模型变量数目的增加，难以获得用于局部模型构建的邻近点，从而造成维度灾难。克鲁伦河流域横跨中蒙两国，流域面积辽阔，不仅STP和STN含量的空间分布上具有异质性，且它们与辅助变量之间的关系也存在异质性。仅使用全局模型将无法拟合复杂的异质性关系，同时由于样点稀少，局部模型难以克服维度灾难问题。因此本文采用两点机器学习（Two-point machine learning, TPML）方法[13]（https://github.com/Bingbo- Gao/TPML），首先利用两点之间土壤属性以及辅助变量的差值建立全局模型，然后基于预测差异建立局部模型。该方法能够有效地处理土壤属性含量自身及其与辅助变量间关系的复杂异质性问题。同时，TPML方法基于点对构建预测模型，能够将原本n的采样点数量扩充至n2，达到样本容量扩充的目的，破解维度灾难，解决土壤采样点稀缺的问题。Gao等[13]证实TPML方法可以有效融合空间位置变量和环境变量，并提供预测结果的不确定性估计，在地球变量观测领域具有广阔的应用前景。王雨雪等[14]使用TPML方法预测黑龙江省海伦市土壤有机质含量，结果表明不同的样本量条件下，TPML方法能够显著提高预测精度。

因此本文基于TPML方法，预测克鲁伦河流域的STN和STP含量，并基于十折交叉检验将其与RF、IDW和OK方法进行对比分析，最后进行克鲁伦河流域STN和STP含量的空间分布制图，获得流域250 m STN和STP含量的空间分布数据。

2 数据采集与处理方法

数据采集地位于克鲁伦河流域（107°25′—117°24′E，46°2′—49°40′N），共有覆盖全流域的STN、STP采样点73个，样方为100 m×100 m。其中有效点71个，50个位于蒙古国区域，21个位于中国境内。STN和STP的采样年份是2022年，单位均为%。

为充分利用STN与STP的空间分布异质性及其与环境变量关系间的异质性[15-16]，本文选取了包括地形、气候、土壤属性、植被及空间位置在内的共18个辅助变量，如表1所示。

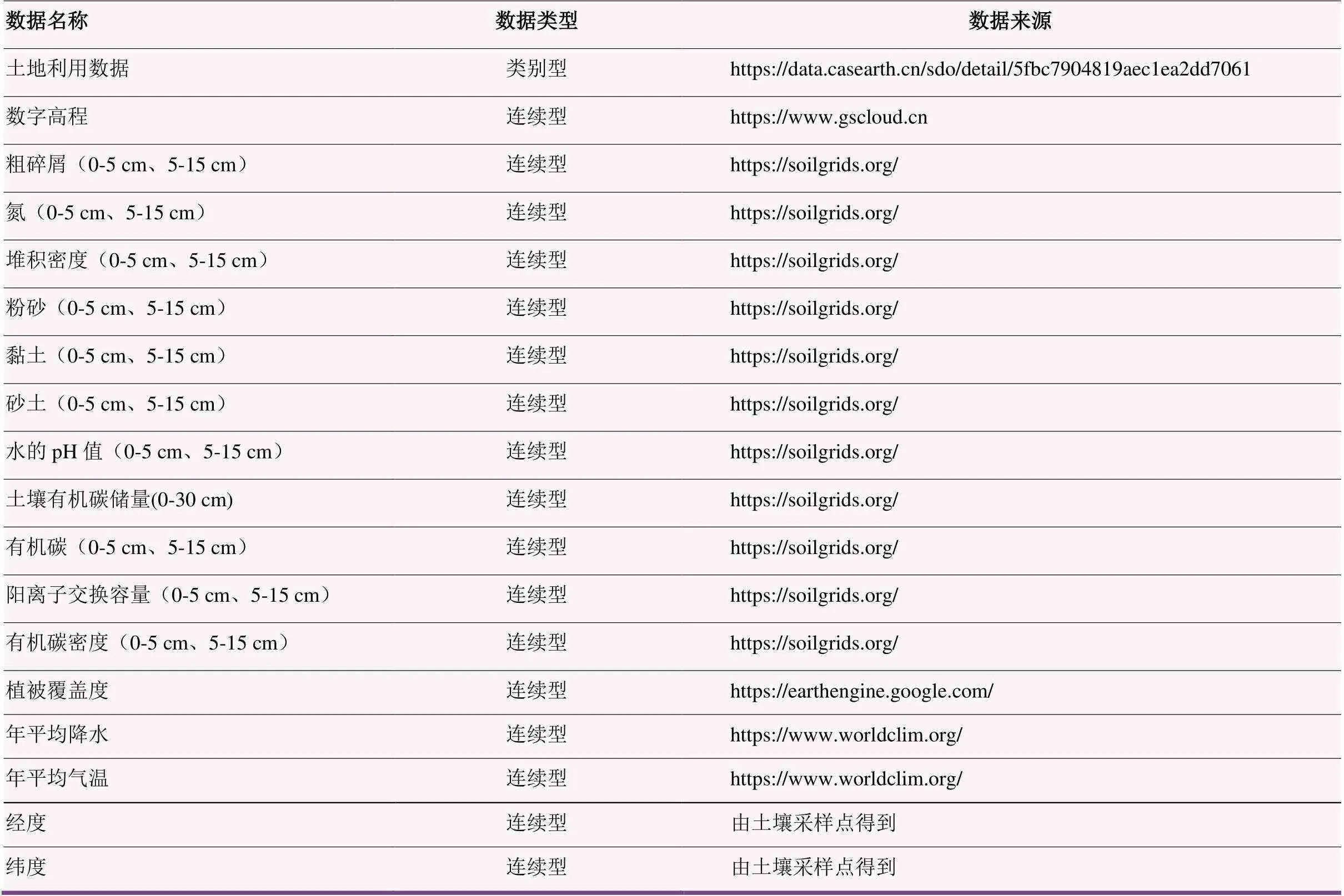
表1 数据类型与来源

除土壤有机碳储量外，分别计算其他0～5 cm、5～15 cm土壤属性栅格的均值。接下来将所有辅助变量数据重采样至250 m，并将所有辅助变量的值提取到采样点上，作为TPML方法中的训练数据集。最终根据栅格数据分辨率生成同尺度的预测点数据，共1855073条数据。

3 数据内容

使用TPML方法得到的250 m克鲁伦河流域STN含量预测结果如图1所示，STN含量的最大值、最小值和平均值分别为2.1463%、0.0013%和0.4086%。STN含量的高值和低值在流域中部呈穿插分布，且从西到东呈现低高低的空间分布模式。STN含量低值主要分布在流域的上游和下游。

250 m克鲁伦河流域的STP含量空间分布如图2所示。基于STP含量的最大值、最小值和平均值分别为6.2736%、0.00001%和1.6236%。STP含量的高值主要位于流域的西南部，流域的西部、北部、中部及东部的STP含量较低。

4 质量控制与技术验证

基于71个土壤采样点数据，选取平均绝对误差（Mean absolute deviation, MAE）和均方根误差（Root mean squared error, RMSE）作为模型评价指标，使用TPML方法进行十折交叉验证，并将其与RF、IDW和OK方法的预测结果进行对比分析，如表2所示。TPML方法预测STN含量的平均MAE和平均RMSE分别为0.309%和0.456%，预测STP含量的平均MAE和平均RMSE分别为0.640%和0.861%。且相较于OK方法，TPML方法预测精度提升超过10%。

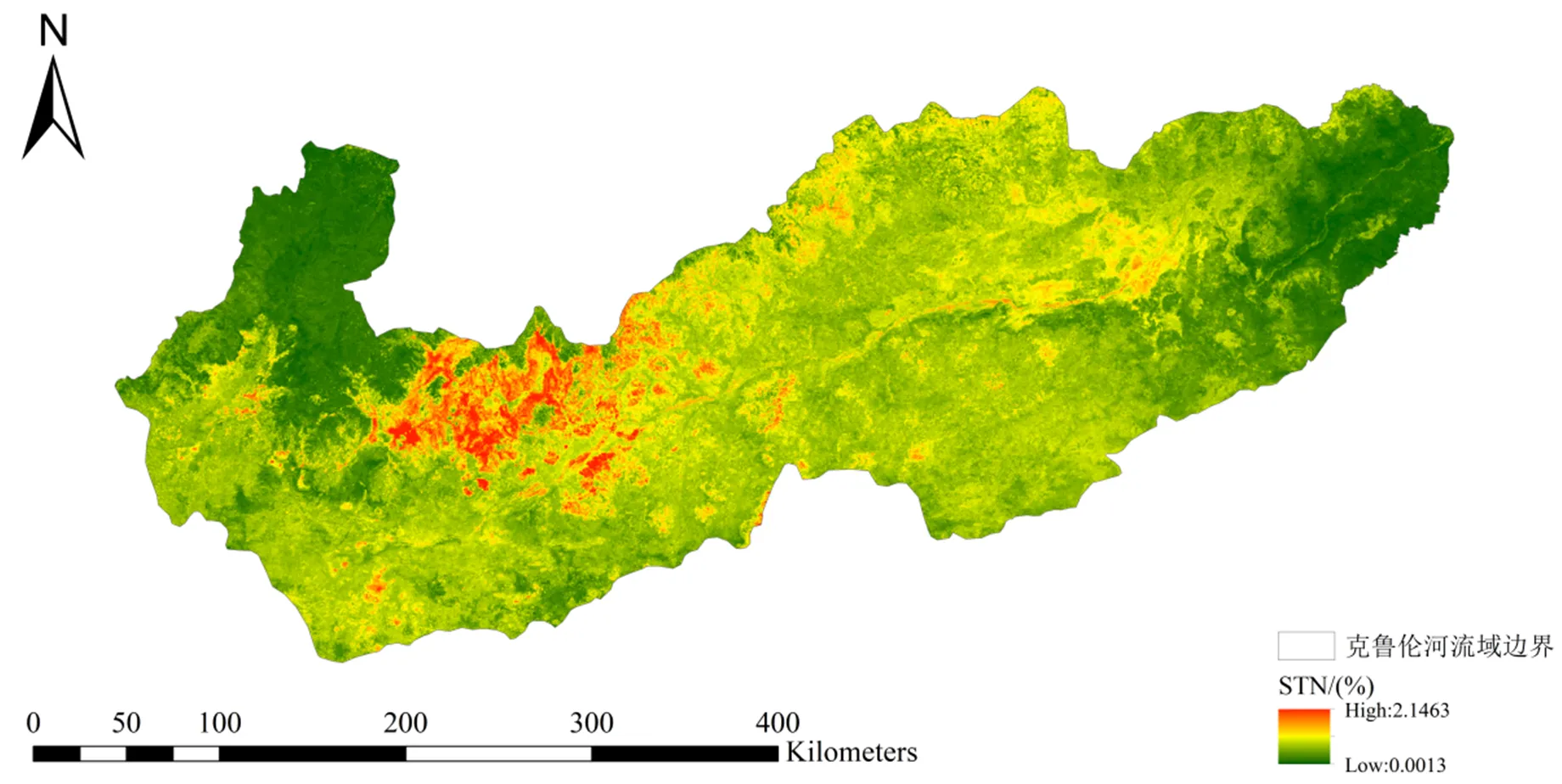
图1 基于TPML方法的克鲁伦河流域STN含量预测结果

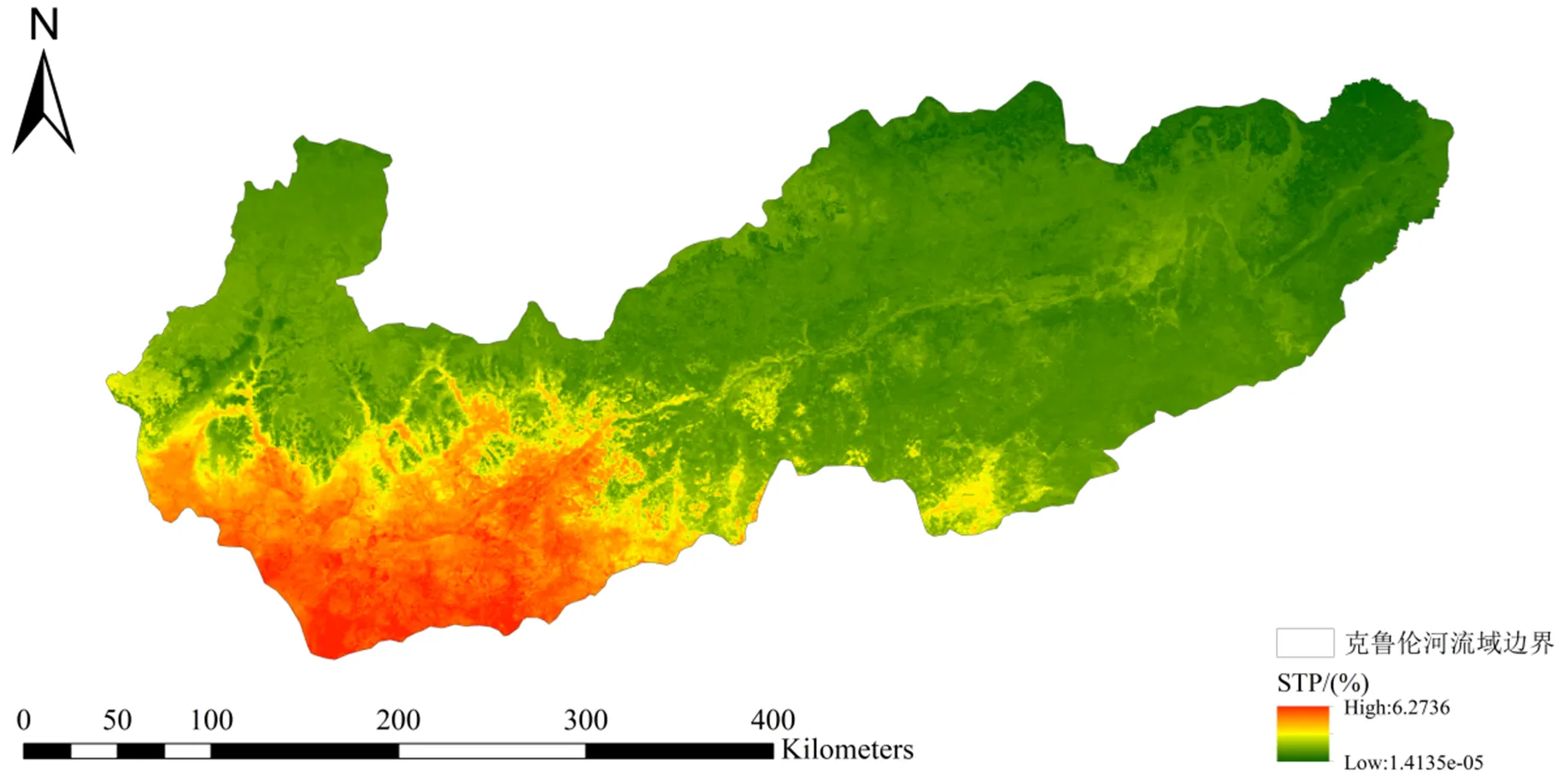
图2 基于TPML方法的克鲁伦河流域STP含量预测结果

结合18个辅助变量，分别使用RF、IDW和OK方法，得到STN含量在克鲁伦河流域的空间分布结果，如图3所示。在三种方法中，OK方法的预测精度较低（图3c），RF方法的预测精度优于OK方法（图3a），但是在克鲁伦河上游地区呈现块状分布。虽然IDW方法交叉检验结果的平均MAE和平均RMSE值低于其他方法，但其对于STN含量空间局部细节的预测能力明显较弱，且该方法仅考虑了点对之间的距离，导致出现围绕样点环状变化的不合理空间分布（图3b）。

三种不同算法预测STP含量的空间分布结果如图4所示，与STN含量的预测情况大致相同，RF方法的预测精度优于IDW与OK方法。RF方法预测STP含量的结果在流域内呈现明显的块状分布（图4a）。且由于IDW方法考虑采样点与待预测点间的距离，所以离采样点较远地区的预测值较低且相近，造成其拥有最低的平均MAE和平均RMSE值，再次证明其利用有限采样点进行大范围土壤属性含量预测时具有局限性（图4b）。

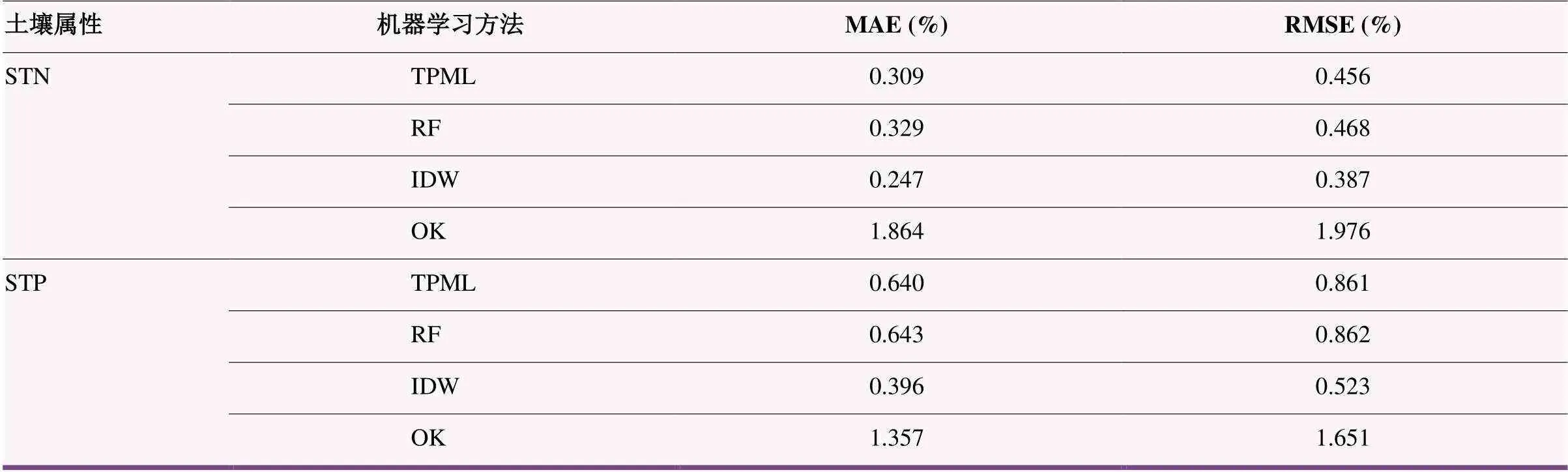
表2 基于十折交叉验证的不同方法预测结果

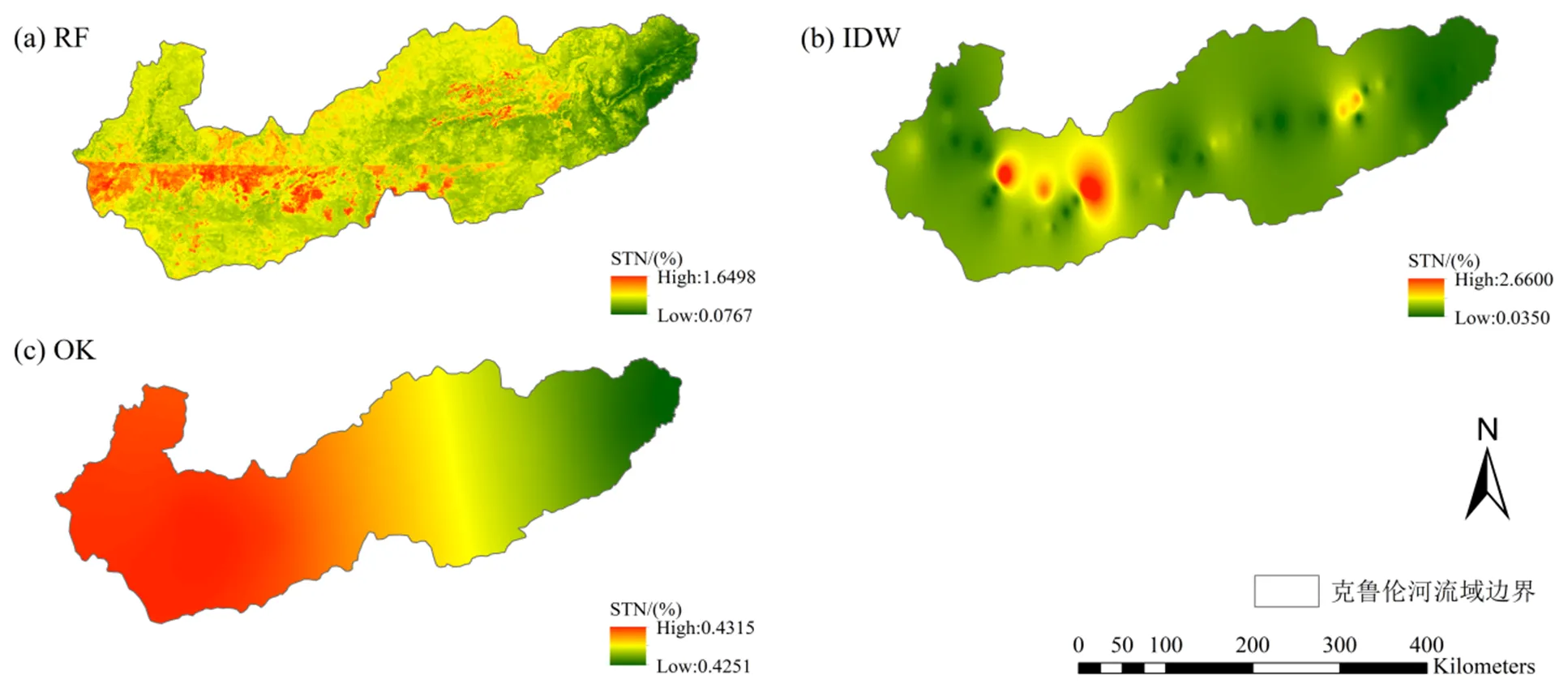
图3 基于不同方法的STN含量预测结果

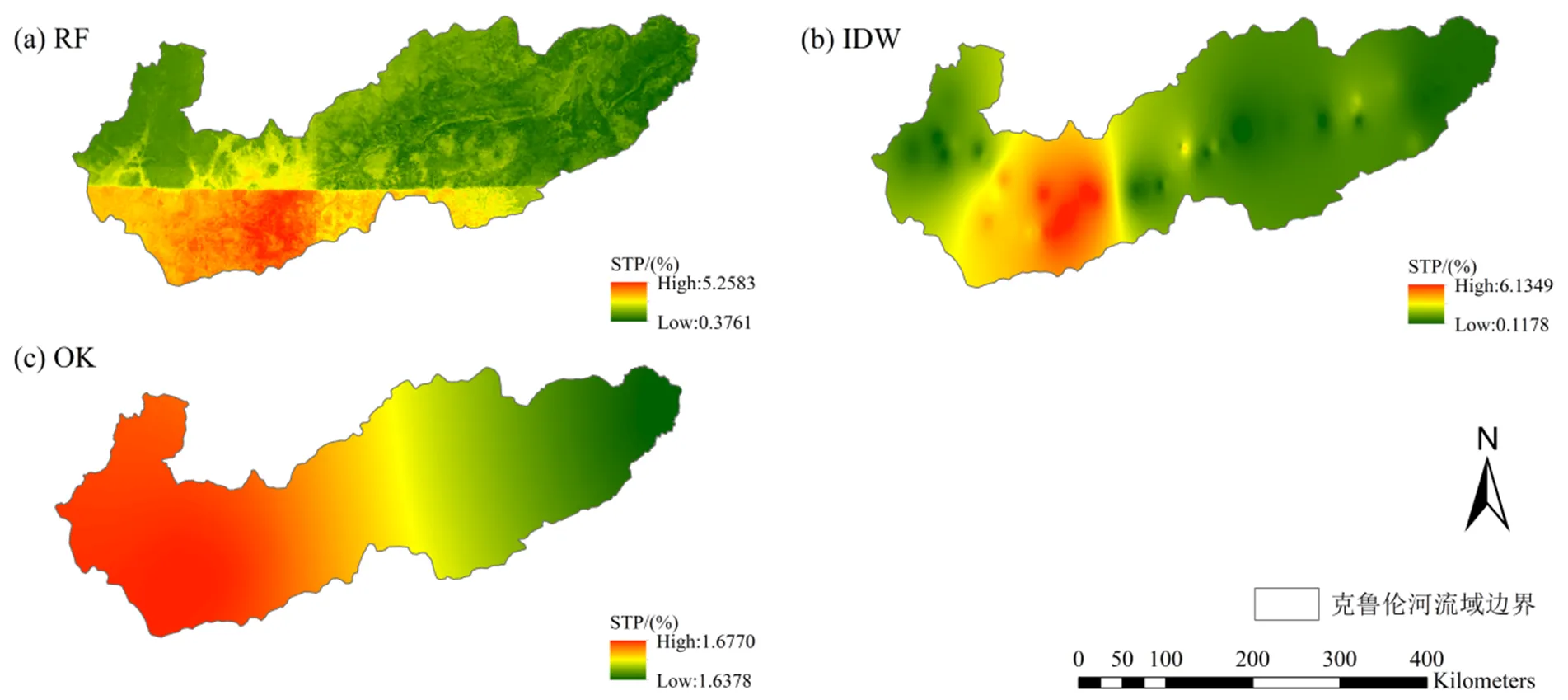
图4 基于不同方法的STP含量预测结果

5 数据价值与使用建议

本数据集包含250m分辨率的克鲁伦河流域STN含量空间分布数据与STP含量空间分布数据，相较于常规的地统计预测方法和机器学习预测方法，数据集使用的TPML方法能充分利用空间位置信息和辅助变量信息，克服空间异质性关系并提高预测精度。因此本数据集有助于探究精细的克鲁伦河流域NPS负荷分布细节，以厘清其来源和数量，同时为流域相关生态环境研究和应用提供数据支撑。

6 数据可用性

中国科技资源标识码（CSTR）：17058.11.sciencedb. agriculture.00018；

数字对象标识码（DOI）：10.57760/sciencedb.agriculture.00018。

允许公开访问。

7 代码可用性

本文所用代码存储于：https://github.com/Bingbo- Gao/TPML。

作者分工与贡献

王辰怡，数据的整理汇总与论文撰写。

高秉博，概念化与方法设计。

Sukhbaatar Chinzorig，项目管理与项目监管。

冯权泷，总体方案设计与论文撰写指导。

冯爱萍，数据质量控制与实验方案设计。

姜传亮，数据的整理汇总与质量控制。

张中浩，论文架构指导与方法设计。

及舒蕊，数据收集与可视化。

利益冲突声明

作者声明，全部作者均无会影响研究公正性的财务利益冲突或个人利益冲突。

[1] Shen Z, Chen L, Ding X, et al. Long-term variation (1960–2003) and causal factors of non-point-source nitrogen and phosphorus in the upper reach of the Yangtze River [J]. Journal of Hazardous Materials, 2013, 252: 45-56. DOI:10.1016/j.jhazmat.2013.02.039.

[2] Shen Q, Wang Y, Wang X, et al. Comparing interpolation methods to predict soil total phosphorus in the Mollisol area of Northeast China [J]. Catena, 2019, 174: 59-72. DOI:10.1016/j.catena.2018.10.052.

[3] Kumar S, Lal R, Liu D. A geographically weighted regression kriging approach for mapping soil organic carbon stock [J]. Geoderma, 2012, 189: 627-634. DOI:10.1016/j.geoderma.2012.05.022.

[4] Wang K, Zhang C, Li W. Predictive mapping of soil total nitrogen at a regional scale: A comparison between geographically weighted regression and cokriging [J]. Applied Geography, 2013, 42: 73-85. DOI:10.1016/j.apgeog.2013.04.002.

[5] Song X-D, Brus D J, Liu F, et al. Mapping soil organic carbon content by geographically weighted regression: A case study in the Heihe River Basin, China [J]. Geoderma, 2016, 261: 11-22. DOI:10.1016/j. geoderma.2015.06.024.

[6] Khaledian Y, Miller B A. Selecting appropriate machine learning methods for digital soil mapping [J]. Applied Mathematical Modelling, 2020, 81: 401-418. DOI:10.1016/j.apm.2019.12.016.

[7] Wadoux A M-C, Minasny B, McBratney A B. Machine learning for digital soil mapping: Applications, challenges and suggested solutions [J]. Earth-Science Reviews, 2020, 210: 103359. DOI:10.1016/j.earscirev. 2020.103359.

[8] 王铭鑫, 范超, 高秉博, 等. 融合半变异函数的空间随机森林插值方法 [J]. 中国生态农业学报(中英文), 2022, 30(3): 451-457. DOI:10.12357/cjea.20210628.

[9] 彭涛, 赵丽, 张爱军, 等. 土壤全氮的无人机高光谱响应特征及估测模型构建 [J]. 农业工程学报, 2023, 39(4): 92-101. DOI:10. 11975/j.issn.1002-6819.202211021.

[10] Hengl T, Leenaars J G, Shepherd K D, et al. Soil nutrient maps of Sub-Saharan Africa: assessment of soil nutrient content at 250 m spatial resolution using machine learning [J]. Nutrient Cycling in Agroecosystems, 2017, 109: 77-102. DOI:10.1007/s10705-017-9870-x.

[11] Gomez C, Chevallier T, Moulin P, et al. Prediction of soil organic and inorganic carbon concentrations in Tunisian samples by mid-infrared reflectance spectroscopy using a French national library [J]. Geoderma, 2020, 375: 114469. DOI:10.1016/j.geoderma.2020.114469.

[12] Ramirez-Lopez L, Behrens T, Schmidt K, et al. The spectrum-based learner: A new local approach for modeling soil vis–NIR spectra of complex datasets [J]. Geoderma, 2013, 195: 268-279. DOI:10.1016/j. geoderma.2012.12.014.

[13] Gao B, Stein A, Wang J. A two-point machine learning method for the spatial prediction of soil pollution [J]. International Journal of Applied Earth Observation and Geoinformation, 2022, 108: 102742. DOI:10. 1016/j.jag.2022.102742.

[14] 王雨雪, 杨柯, 高秉博, 等. 基于两点机器学习方法的土壤有机质空间分布预测 [J]. 农业工程学报, 2022, 38(12): 65-73. DOI:10. 11975/j.issn.1002-6819.2022.12.008.

[15] 霍明珠, 高秉博, 乔冬云, 等. 基于APCS-MLR受体模型的农田土壤重金属源解析 [J]. 农业环境科学学报, 2021, 40(05): 978-986.

[16] Wang Q, Xie Z, Li F. Using ensemble models to identify and apportion heavy metal pollution sources in agricultural soils on a local scale [J]. Environmental Pollution, 2015, 206: 227-235. DOI:10. 1016/j.envpol.2015.06.040.

Dataset of Soil Total Nitrogen Content and Soil Total Phosphorus Content of the Kherlen River Basin in 2022

WANG ChenYi1, GAO BingBo1*, Sukhbaatar Chinzorig2, FENG QuanLong1, FENG AiPing3, JIANG ChuanLiang1, ZHANG ZhongHao4, JI ShuRui1

1College of Land Science and Technology, China Agricultural University, Beijing 100083, China;2Institute of Geography and Geoecology, Mongolian Academy of Sciences, Ulaanbaatar 15170, Mongolia;3Ministry of Ecology and Environment Center for Satellite Application on Ecology and Environment, Beijing 100094, China;4College of Environmental and Geographical Sciences, Shanghai Normal University, Shanghai 200234, China

The ecological and environmental security of the Kherlen River Basin has attracted more and more attention in China and Mongolia. It is of great significance to investigate the contents of soil total nitrogen (STN) and soil total phosphorus (STP) in the basin for accurately estimating the load of non-point sources (NPS) and studying the state of resources and environment and sustainable development. It is time-consuming and labor-intensive to obtain a wide range of STN and STP contents using traditional sampling methods, while STN and STP not only have spatial heterogeneity, but also have heterogeneity in their relationships with auxiliary variables. Moreover, a single global model cannot fit complex heterogeneous relationships, and it is difficult for the local modeling method to overcome dimensional disaster problems. Therefore, the two-point machine learning (TPML) method is introduced in this paper. The TPML method first establishes a global model based on the difference of paired points, and then constructs a local model based on the prediction difference of the global model. It can expand the sample size from n to n2, achieving the prediction of high-precision and large-scale STN and STP contents using limited sampling points. Based on 18 auxiliary variables of topography, climate, soil properties, vegetation and spatial location, etc, the study produced the distribution dataset of STN and STP contents in the basin using the TPML method. Futhermore, using the ten-fold cross-validation method, the study confirmed that the prediction accuracy of TPML model is more than 10% higher than that of Ordinary Kriging (OK) model. The mean absolute deviation (MAE) and mean root mean squared error (RMSE) of STN content predicted by the TPML method are 0.309% and 0.456% respectively. The mean MAE of STN content predicted by random forest (RF), inverse distance weighted (IDW) and OK methods is 0.329%, 0.247% and 1.864%, and the mean RMSE is 0.468%, 0.387% and 1.976%, respectively. The mean MAE and mean RMSE of STP content predicted by TPML method are 0.640% and 0.861%. The mean MAE of STP content predicted by RF, IDW and OK methods is 0.643%, 0.396% and 1.357%, and the mean RMSE is 0.862%, 0.523% and 1.651%, respectively.

Kherlen River Basin; two-point machine learning; soil total nitrogen; soil total phosphorus

Data summary:

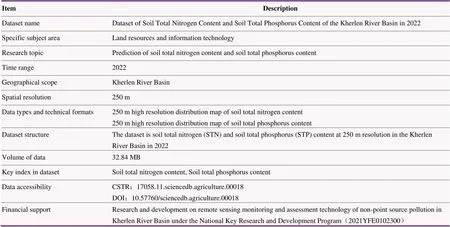
ItemDescription Dataset nameDataset of Soil Total Nitrogen Content and Soil Total Phosphorus Content of the Kherlen River Basin in 2022 Specific subject areaLand resources and information technology Research topicPrediction of soil total nitrogen content and soil total phosphorus content Time range2022 Geographical scopeKherlen River Basin Spatial resolution250 m Data types and technical formats250 m high resolution distribution map of soil total nitrogen content250 m high resolution distribution map of soil total phosphorus content Dataset structureThe dataset is soil total nitrogen (STN) and soil total phosphorus (STP) content at 250 m resolution in the Kherlen River Basin in 2022 Volume of data32.84 MB Key index in datasetSoil total nitrogen content, Soil total phosphorus content Data accessibilityCSTR：17058.11.sciencedb.agriculture.00018DOI：10.57760/sciencedb.agriculture.00018 Financial supportResearch and development on remote sensing monitoring and assessment technology of non-point source pollution in Kherlen River Basin under the National Key Research and Development Program（2021YFE0102300）

王辰怡, 高秉博, Sukhbaatar Chinzorig, 冯权泷, 冯爱萍, 姜传亮, 张中浩, 及舒蕊. 2022年克鲁伦河流域土壤全氮含量与土壤全磷含量数据集[J]. 农业大数据学报, 2023, 5(3):104-111.

WANG ChenYi, GAO BingBo, Sukhbaatar Chinzorig, FENG QuanLong, FENG AiPing, JIANG ChuanLiang, ZHANG ZhongHao, JI ShuRui. Dataset of Soil Total Nitrogen Content and Soil Total Phosphorus Content of the Kherlen River Basin in 2022 [J]. Journal of Agricultural Big Data, 2023, 5(3): 104-111.

数据摘要：

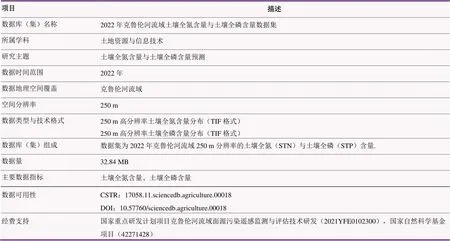
项目描述 数据库（集）名称2022年克鲁伦河流域土壤全氮含量与土壤全磷含量数据集 所属学科土地资源与信息技术 研究主题土壤全氮含量与土壤全磷含量预测 数据时间范围2022年 数据地理空间覆盖克鲁伦河流域 空间分辨率250 m 数据类型与技术格式250 m高分辨率土壤全氮含量分布（TIF格式）250 m高分辨率土壤全磷含量分布（TIF格式） 数据库（集）组成数据集为2022年克鲁伦河流域250 m分辨率的土壤全氮（STN）与土壤全磷（STP）含量. 数据量32.84 MB 主要数据指标土壤全氮含量、土壤全磷含量 数据可用性CSTR：17058.11.sciencedb.agriculture.00018DOI：10.57760/sciencedb.agriculture.00018 经费支持国家重点研发计划项目克鲁伦河流域面源污染遥感监测与评估技术研发（2021YFE0102300），国家自然科学基金项目（42271428）