斜压大气中任意频率惯性重力内波不稳定的判据
2023-11-17豆京华
吴 洪,牛 宁,豆京华
(1.中国气象局气象干部培训学院,北京 100081;2.中国气象局气象干部培训学院河北分院,河北保定 071000)
0 引言
描述中尺度运动的控制方程组,包含的特征波动是频谱较广的重力波,采用Boussinesq 近似后,该方程组包含的特征波动则是低频的重力波,如惯性重力内波[1]。惯性重力内波常与暴雨、台风、强对流等天气有关[2-8]。
考虑基本气流具有水平和垂直切变,刘式适等[9],李崇银等[10]分析讨论了惯性重力内波的不稳定性。同样在具有水平和垂直切变基本气流的大气中,B J Hoskins[11],D A Bennetts 等[12],陆汉城等[1]采用大气线性波动的分析方法,得出对称不稳定的判据。不少气象学家利用“气块法”也得到对称不稳定的判据[13-16]。这两类不稳定判据的表达式是相同的,即等熵面坡度大于等绝对动量面的坡度,似乎表明对称不稳定与惯性重力内波不稳定是相互对等的。对称不稳定理论被广泛运用于解释中纬度的带状降雨[17-25]。对称不稳定判据的普及应用性远大于惯性重力内波不稳定,但这个不稳定的判据,只有当波动或扰动的频率为最小时才成立。但对称不稳定和惯性重力内波不稳定的判据,都只是在设定波动频率或振动(扰动)频率最小时推导出来的,且这个最小频率在波动等位相面[1,9-12]为特定值时才具有。
大气中惯性重力波具有比较宽的频谱。在斜压大气中,为了解惯性重力内波的频率方程、任意频率的惯性重力内波,其稳定性及判据等,本文采用标准的正交模方法,着重分析斜压大气中任意频率的惯性重力内波的稳定性,得到相应的波动不稳定性及其判据,以期更合理地应用在带状云系和降水发生发展的机理研究和实际业务中。
1 斜压大气中的惯性重力内波
满足绝热、无摩擦的Boussinesq 近似的大气运动方程组,可用于描述惯性重力内波[1,9-10,13-15,26-27]:
式中,u、v、w表示空气块运动的x、y、z方向的速度分量;p是气压场,p′是相对基本状态气压场的偏差;ρ为空气密度,ρ0表示基本状态的空气密度的典型值,为常数;,θ′是相对位温基本状态的偏差,θ0表示基本状态的位温的典型值,为常数;f0为地转参数,对惯性重力内波可取为常数。式(1)表明大气运动是非静力平衡的。
1.1 频率方程
不失一般性,假定扰动只在y-z平面内,即与x无关。将式(1)线性化,得到描述波动的方程组:


将用流函数表示的扰动速度代入式(2),消去其他扰动量,仅保留流函数,得
对于“无界”大气,可设波动的形式解为Ψ=Aei(ly+mz-ωt),ω、l、m分别表示惯性重力内波的频率、y方向的波数、z方向的波数。代入式(3)进一步运算得斜压大气中惯性重力内波的频率方程
由式(4)可知,如果惯性重力内波只在y或z方向传播,即m≡0 或l≡0,则式(4)蜕变为浮力振荡或惯性振荡,显然式(4)作为惯性重力内波的频率方程,l、m均不等于零。惯性重力内波的最小、最大频率分别为[1,9-10,13]
1.2 相速与群速
令K2≡l2+m2,K表示二维波动的波数,→K≡l→j+m→k。波动的相速为
波动的群速:
由式(6)、(7)可得
在具有水平和垂直切变的基流中,惯性重力内波的传播方向(相速度)与能量传播方向(群速度)相互垂直,这一性质与不考虑基本气流的惯性重力内波的一致。
2 斜压大气中的惯性重力内波稳定性
由于惯性重力内波的波数l、m均不等于零。令φ=ly+mz-ωt表示波动的位相,当其等于常数时表示波动等位相面。则等位相面的倾斜率:
其中α为等位相面与y轴正向的夹角。
根据惯性重力内波形成的原理,只有在层结稳定N2>0 和惯性稳定F2>0 的环境大气中,惯性重力内波才能形成,即一般N2l2+F2m2>0。由式(4)可知,当ω2>0时,惯性重力内波是稳定的;反之,惯性重力内波是不稳定的。因此,若ω2<0,必须:
式(9)即是斜压大气中惯性重力内波不稳定的必要条件。
环境大气的风一般是随高度增大的,在北半球S2>0,则惯性重力内波不稳定的必要条件可改写为
由式(8)可知,式(10)可以改写为

图1 等位相面示意图(α 是等位相面与y 轴的夹角,t0、t1 分别表示不同的时刻)
如果环境大气基本气流随高度减小时,在北半球S2<0,则此时惯性重力内波不稳定的必要条件为
式(12)表明,风速随高度减小时,惯性重力内波不稳定的必要条件是等位相面向南倾斜,波动向北(南)、向上(下)传播。多普勒天气雷达监测表明,有时低空急流表现出“轴状”的结构,即其下风速随高度增大、而其上一定的层次内风速随高度减小,因此,当低空急流呈“轴状”结构时,其上的环境大气S2<0。
一般情况下N2>0,F2>0,由式(4)可知,斜压大气中惯性重力内波不稳定的充分条件为
利用式(8),式(13)可改写为
令
由于N2>0,因而当Δ>0,即S4>N2F2时,若
式(14)成立,即惯性重力内波不稳定;若Δ=0 或Δ<0时,式(14)均无解,即无论波动等位相面如何倾斜,tgα为任何值,波动都是稳定的。


频率方程式(4)可改写为
式中:
其中,b恒大于零。

若环境大气是层结不稳定的层结,N2<0,则令
式(14)改写为
设
当环境大气是惯性稳定的,F2>0,可知>0,即S4>N2F2。此时,若要式(20)成立,即惯性重力内波不稳定,必须是波动等位相面的倾斜度满足tgα>,或;否则,波动稳定。当环境大气是惯性不稳定的,F2<0,若S4-N2F2>0,则惯性重力内波不稳定的充分条件依然是,或tgα<;若S4=N2F2,惯性重力内波不稳定的充分条件是,即波动的等位相面、环境大气的等熵面和等绝对动量面三者不能重合;若S4<N2F2,无论波动的等位相面的倾斜度如何,波动都将是不稳定的。可见,环境大气层结不稳定时,对流所激发的惯性重力内波的稳定性变化非常复杂,可能发生稳定,也可能发生不稳定。
若环境斜压大气是中性层结,N2≡0,惯性重力内波变为纯惯性内波。其稳定性的判据为
或
若环境大气基本气流随高度减小,S2<0,则此惯性内波恒稳。

若不考虑地球自转作用,F2≡0,惯性重力内波变为纯重力内波,其稳定性的判据为
或
3 静力平衡的影响
由物理机制可知,只有大气出现不断变化的水平辐散、辐合作用,使得气块在铅直方向出现上下运动并随时间变化,才可形成惯性重力内波[13-15,26-27]。
由式(18)可得
式(27)与式(26)中的第3 个方程分别表示扰动的水平散度不随时间变化、气块的铅直运动不随时间变化,这直接破坏了惯性重力内波形成的物理机制,即大气中不能形成惯性重力内波,也就不存在该波动的稳定性。因此,在Boussinesq 近似的大气运动方程组中不能采用静力平衡条件。
4 结论
利用绝热、无摩擦、Boussinesq 近似的大气运动方程组,采用小扰动法和正交模法,得到斜压大气中惯性重力内波的频率方程,着重分析、讨论任意频率惯性重力内波的稳定性。主要结论如下:
(1)当大气是层结稳定、惯性稳定,且基本气流随高度增大时,惯性重力内波不稳定的必要条件是等位相面向北倾斜;若基本气流随高度减小,惯性重力内波不稳定的必要条件是等位相面向南倾斜。
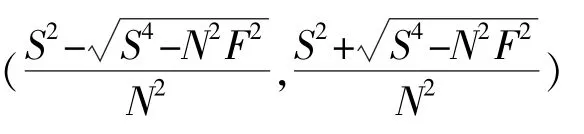

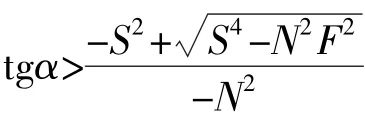

(6)用Boussinesq 近似的大气运动方程组讨论惯性重力波或重力波或惯性波时,不能采用静力平衡条件。

本文只是从理论上讨论斜压大气中惯性重力内波不稳定的判据,在实际中如何应用,乃是今后进一步研究工作的方向。
