6 kA稀土钕电解槽多相流动数值模拟
2023-11-17文棠根张斌张家微李明周杨少华
文棠根, 张斌*, 张家微, 李明周, 杨少华
(1.江西理工大学材料冶金化学学部,江西 赣州 341000; 2.赣州晨光稀土新材料有限公司,江西 赣州 341000)
我国的稀土资源储量最多,约占世界稀土总量的36.67%。单一稀土金属、混合稀土金属和稀土合金的制取多采用熔盐电解法[1-2]。大多数稀土电解厂多采用上插阴阳极式电解槽。生产过程中,稀土氧化物在熔融电解质中离解出稀土离子,在电场作用下向阴极移动并在阴极上析出稀土金属,阳极上产生的氧气与石墨阳极发生化学反应生成CO2和CO,气泡通过熔融电解质从顶部表面逸出[3-4]。阳极气泡的上浮流动带动了电解质在电解槽内循环流动,循环产生的搅拌作用,使从顶部加入的稀土氧化物颗粒快速溶解在槽内电解质中,同时使槽内电解质浓度和温度趋于均匀[5]。
近年来,许多学者结合计算流体力学(CFD)和数值模拟方法优化电解槽的结构和工艺参数,对稀土电解过程的多物理场进行仿真研究[6-7],为我国稀土电解技术的进步做出了重要贡献[8-10]。刘中兴等[11]模拟了3 kA钕电解槽的流场,得出了电磁力及气泡浮力共同作用下的熔体流场分布情况。伍永福等[12]将电解槽简化为二维问题,并建立了二维非稳态气-液-液多相流动模型,计算得到了不同时间的流场分布和钕液浓度分布。刘宇新等[13]建立了二维气-液两相流数学模型,并考虑了表面化学反应,得到了电解槽的流场和气体浓度分布。刘钊等[14]采用雷诺应力模型对电解槽内部流场进行模拟,发现通过底吹气体能够在一定程度上改善电解槽底部的流动性,减轻底部“结瘤”现象。逄启寿等[15]模拟了稀土电解槽三维流场,得出了流场及流速的变化规律。伍永福等[16]对稀土电解槽电场-流场进行耦合数值模拟,分析了阳极生成气体对电场产生的影响。高钰奇等[17]建立了3 kA稀土电解槽的流场分布模型和DPM离散相模型,模拟了氧化钕的下料过程,通过改变电极插入的深度来探究颗粒的运动过程。
稀土电解槽内气泡、电解质的流动过程决定了温度、浓度、电场的分布,最终影响稀土金属的析出和电解效率。本文利用ANSYS-FLUENT软件对6 kA上插阴极电解槽进行数值模拟研究,定量分析稀土钕电解槽内气泡、电解质、稀土金属的非稳态流动过程,为分析电解槽多相流动特点、优化工艺技术参数提供理论依据。
1 数学模型及边界条件
1.1 模型假设
为了分析稀土电解槽内流动情况,做以下假设:①电解槽内流体包括电解质、气泡、稀土金属;②阳极产生的气体为CO2,为不可压缩流体;③稀土金属在阴极析出,气泡在阳极内壁面生成;④不考虑壁面滑移速度。
1.2 数学模型
质量守恒方程即连续性方程,其表达式[18]为:
式(1)中:ρ为密度;t为时间;U为流场中任一点的流速。
动量守恒方程:
式(2)中:p为表面压力;g为重力加速度;μ为动力黏度;f为体积力。
VOF方法[19]是建立在欧拉网格下的界面追踪方法。在VOF模型中,不同流体组分共用一套动量方程,计算时在全流场的每个计算单元内都记录各相组分所占的体积分数或体积率。可以显示多相流的界面运动情况,其适用于自由表面流和分层流。在VOF模型中,在互不相容的流体组分中共用一套动量方程,并引入相体积分数α。
VOF的动量方程:
式(3)中:ρ为密度;P为压力;g为重力加速度;U为流体速度;μ为有效黏度;F为体积力。
VOF模型的相方程:
式(4)中:p、q为相;ρ为密度;α为体积分数;Sαq为源相。为两相间的质量输送。
在稀土电解槽几何模型中,电解质占多数体积,计算时将电解质设为主相,阳极气泡设为第一次相,液体稀土金属设为第二次相。
电解槽内为湍流流动,本文使用Realizablek-ε湍流模型进行计算[20]。
1.3 边界条件
1.3.1 几何条件
以某6 kA上插阴极圆筒形稀土钕电解槽为对象,建立二维和三维几何模型,如图1(a)和图1(b)所示。电解槽高0.71 m,槽内径0.42 m,阳极炭块厚度0.12 m,阴极直径0.06 m,电极插入深度0.45 m,电解质高度0.61 m,空气区域0.1 m,其中三维几何模型采用分块阳极结构,相邻阳极之间存在缝隙。二维几何模型为穿过三维模型阴阳极的截面。

图1 稀土电解槽模型结构图:(a) 电解槽二维模型;(b) 电解槽三维模型Fig.1 Structure diagram of rare earth electrolytic cell model:(a)2D model of electrolytic cell;(b)3D model of electrolytic cell
对稀土电解槽二维模型计算区域进行网格划分,使用最小网格尺寸为10 mm矩形网格,网格数量1 823个;对稀土电解槽三维模型计算区域进行网格划分,对于电解质区域使用最小网格尺寸为13 mm的四面体网格,空气区域性质比较规则,使用最小网格尺寸为13 mm的六面体网格,网格数量20万个。二维和三维网格如图2 所示。

图2 计算区域网格划分:(a)二维网格 ;(b)三维网格Fig.2 Mesh of calculation region:(a)2D mesh;(b)3D mesh
1.3.2 物性参数
电解质选用NdF3-LiF-Nd2O3,工作温度下熔体部分物质物性参数如表1所列[11-15]。

表1 电解质物性参数[11-15]Table 1 Electrolyte physical parameters[11-15]
1.3.3 进出口边界条件
稀土金属从阴极析出,设置阴极壁面为质量流量入口边界条件。稀土金属在气泡停留阳极内壁期间产生的稀土金属质量G为[21-23]:
式(5)中:C为电化当量数值,单位A/h;t为气泡停留时间数值,单位s;η为电流效率数值,单位%。
稀土金属的质量流量qm为:
阳极气泡从阳极内壁逸出,设置阳极内壁为速度入口边界条件。阳极二氧化碳生成量n为:
在1 050 ℃,1 mol气体体积按理想气体计算为22.4 L,单位时间产生气体的体积流量qv为:
相邻阳极之间存在10°的空隙,则单位时间产生气体的流速v为:
出口为电解质顶部自由液面,确定为压力出口边界,出口选择标准大气压力,101 325 Pa;固体壁面采用无滑移壁面。
2 模型求解及验证
2.1 数学模型求解设置
使用数值模拟软件FLUENT对建立的模型进行求解。速度耦合采用SIMPLE算法,压力基分离器用PRESTO格式,动量方程用一阶迎风格式,设置计算步长为0.005 s。
2.2 网格独立性验证
由于阳极底部受到气泡流和稀土金属的湍流流动影响较小,流动稳定,在此区域附近设置相邻的2个监测点,其中监测点1的坐标为(0.1,0.1,0),监测点2坐标为(0.09,0.1,0)。监测两点在不同时刻的速度变化,进行网格独立性验证。对三维几何模型划分网格, 最小网格尺寸分别为16、 13、 12 mm,网格数量分别为125 831、226 917、330 314个。计算得到不同时刻不同网格数量下监测点的速度如图3所示。

图3 不同网格数量下监测点速度:(a)监测点1;(b)监测点2Fig.3 Outlet velocity under different grid numbers:(a) monitor point 1;(b) monitor point 2
由图3(a)、图3(b)可以看出,在10万个网格和20万个网格条件下,监测点1、监测点2相同时刻的速度相差大;在20万个网格与30万个网格条件下,监测点1、监测点2相同时刻的速度基本一致。因此本文对三维模型选择20万个网格进行计算,减少计算成本。
2.3 模拟结果验证
本文根据其他学者论文的模型参数设置[14],计算得出的二维电解槽内速度分布如图4(a)所示,参考文献中速度分布如图4(b)所示。

图4 模拟结果验证:(a) 计算得出电解槽内速度分布;(b) 文献[14]中电解槽内速度分布Fig.4 Verification of simulation results:(a)calculated velocity distribution in electrolytic cell;(b)velocity distribution in electrolytic cell in the references[14]
从图4(a)中可以看出,电解产生的气体主要集中在阳极内壁面附近,最大上升流速为0.9 m/s,而槽底位置流速较小。此计算结果与图4(b)参考文献[14]中电解槽速度分布结果基本一致。
3 模拟结果讨论
模拟计算二维和三维稀土电解槽的流场分布并进行对比。计算均一极距和非均一极距流场分布,以定量分析实际电解槽内流动特性。
3.1 二维与三维流场对比
3.1.1 电解槽中相分布
图5所示为当气泡稳定上升稀土金属稳定析出时二维模型和三维均一极距模型的阳极气泡-电解质-稀土金属三相分布。其中图5(a)为二维模型三相分布,图5(b)为三维模型截面选取示意图。在三维几何模型中截取穿过阴极和2个阳极的平面为截面A,穿过阴极和阳极孔隙的平面为截面B,图5(c)、图5(d)为截面A、B的多相分布图。

图5 二维和三维相分布图:(a) 二维模型三相分布;(b) 三维截面示意图 (c) A 截面三相分布;(d) B 截面三相分布Fig.5 Distribution of two dimensional and three-dimensional phase:(a) distribution of three phases in 2D model;(b) cross section diagram in 3D model;(c) distribution of three phases in cross section A;(d) distribution of three phases in cross section B
从图5可以看出,二维和三维模型均能模拟电解槽内部三相流动过程:气泡从阳极内表面生成,并沿着阳极壁面上升;稀土从阴极析出,并呈液滴的形式滴落到底部的收集槽中。上升的气泡流到达顶部自由液面时导致液面波动。由于阴阳极距相同,在阴极上析出的稀土金属竖直落入底部坩埚,没有发生偏斜。
3.1.2 速度流线对比
图6所示为二维和三维模型的速度分布图和流线图,其中图6(a)为二维模型流线分布,图6(b)为三维流线分布,图6(c)为三维模型中截面A的流线分布,图6(d)为三维模型截面B的流线分布。

图6 速度分布云图和流线分布: (a) 二维流线图;(b) 三维流线分布;(c) 截面A 流线分布;(d) 截面B 流线分布Fig.6 Distribution of velocity and streamline: (a) diagram of 2D streamline;(b) distribution of 3D streamline;(c) streamline in cross section A;(d) streamline in cross section B
从图6(a)可看出,随着气泡流的上升和稀土金属的下降,电解质在槽内形成循环流动,在阴极、阳极之间顶部和底部区域形成了两对旋涡,但在阳极外侧电解质流速为0,且在电解槽底部边缘处存在流速较小,即存在流动死区。从图6(b)中可见,电解槽内流动循环包括阴阳极间的“内循环”和阳极内外侧的“外循环”。图6(c)表明,电解质不仅能够在阴阳极间流动,在阳极外侧同样具有一定流速,甚至存在漩涡,该现象与二维模型计算结果不同。此外,阴极、阳极之间顶部漩涡处流线密度较大而底部漩涡处流线密度较稀疏,即底部漩涡的旋流强度较弱,对稀土金属的析出影响较小。图6(d)表明,电解质在阳极炭块之间的空隙具有径向速度,即电解质会从空隙处沿径向流动到阳极外侧区域,使整个电解槽内流体进行动量、能量和质量充分交换,而在底部存在对称的漩涡。
图7所示为三维模型沿电解槽高度横截面z=0.61 m的速度云图和流线分布。

图7 z=0.61 m横截面速度流线Fig.7 Velocity streamline of z = 0.61 m cross section
从图7可以看出,阳极内壁面处气泡快速上升,流速较大。电解质在阳极之间空隙存在径向速度,从阳极内测流动到阳极外侧区域,阳极外侧区域甚至也会产生漩涡。综合图6和图7表明,尽管二维电解槽模型能够计算出槽内多相流动过程,但无法模拟出阳极空隙处及阳极外侧的流动过程,与实际生产过程不符。而三维模型能够模拟出完整、详细的电解槽内多相流动过程,更加准确地反映实际稀土电解槽电解生产的流动特性。
3.2 非均一极距流场分析
实际生产过程中,石墨阳极内表面会被不断氧化而变薄,使得阴阳极间距发生变化。当阳极变薄到一定厚度需要对其进行更换。生产中阳极并非4片同时更换,而是按顺序逐一更换,由此导致实际稀土电解槽中阴阳极极距不相等。不同极距会导致电流密度、电压降、发热量等参数发生变化,从而影响气体生成量、电解质流速、湍流强度。
本文建立了不同阳极厚度非均一极距几何模型,并对4片阳极按照逆时针顺序从1到4进行编号,如图8所示。阳极厚度和极距如表2所列。在模型中取穿过1、3号阳极的平面为截面C,穿过2、4号阳极的平面为截面D。在非均一极距条件下电流强度的改变使气泡初始速度发生改变,根据前文公式计算得出气泡析出速度分别为0.005 6、0.005 2、0.004 8、0.004 4 m/s。

表2 不同阳极参数Table 2 Different anode parameters

图8 非均一极距几何模型Fig.8 Geometric model of non-uniform polar distance
3.2.1 流速及漩涡位置分布
计算得出在稳定状态下电解槽内的流场分布,图9 所示为三维稀土电解槽C、D 截面速度矢量图。

图9 速度矢量图:(a) C 截面速度矢量; (b) D 截面速度矢量Fig.9 Diagram of velocity vector:(a) velocity vector in cross section C; (b) velocity vector in cross section D
从图9中可以看出,随着极距的变化,在电解槽上部阴阳极之间产生的旋涡位置和形状会发生改变。随着极距增加,漩涡面积不断增大,即电解质运动范围变大;漩涡形状由扁平变得接近圆形,且电解质流速逐渐降低,即漩涡的搅拌作用减弱。
为了定量分析电解质旋涡位置,以阴极轴线和电解槽底部相交点为坐标原点,计算得出1—4号阳极对应旋涡中心径向距离和轴向距离,如图10所示。

图10 阳极旋涡涡心位置: (a) 涡心径向距离; (b) 涡心轴向距离Fig.10 Position of vortex center of anode vortex: (a) radial distance of vortex center; (b) axial distance of vortex center
从图10可以看出,随着极距增加,1—4号阳极产生的旋涡径向距离不断增大,即旋涡向着阴极方向靠近。1—4号阳极产生的旋涡轴向距离不断减小,即旋涡向着电解质底部发展。
图11所示为C、D截面流场速度云图。

图11 不同截面速度分布云图:(a) C 截面速度分布;(b) D 截面速度分布Fig.11 in different cross section: (a) velocity distribution in cross section C;(b) velocity distribution in cross section D
从图11中可以看出,电解槽顶部阴阳极之间靠近壁面区域速度最大,达0.7 m/s。在阴极下方随着稀土金属的滴落以及电解质漩涡的影响,其流速为0.6 m/s。在阳极外侧以及电解槽底部靠近壁面处速度较均匀。由于极距变化导致流场发生较大变化,最终导致从阴极上析出的稀土金属发生偏斜。
3.2.2 流线及相分布
计算得出非均一极距下电解槽内的流线分布,图12所示为C截面的流线分布图和相分布图。

图12 C截面速度分布及多相分布: (a) 速度及流线分布图; (b) 三相分布图Fig.12 Distribution of velocity and phases in cross section C:(a) distribution of velocity and streamline; (b) distribution of three phases
从图12(a)可以看出,由于3号阳极变薄,极距变大,气泡上升带动电解质产生循环流动在该区域充分发展,使得旋流区域扩大,3号阳极底部漩涡的旋流强度增大。1号和3号阳极底部漩涡的旋流强度不同,导致从阴极析出的稀土金属在左右两侧具有不同的流动速度。图12(b)中红色部分为在阴极上析出的稀土金属,蓝色区域为气相,绿色区域为电解质。由于右侧旋流强度较大,最终使稀土金属向旋流速度较低的一侧发生偏斜。同样在D截面也会发生类似的情况,如图13所示。

图13 D 截面速度分布及多相分布:(a) 速度及流线分布图;(b) 三相分布图Fig.13 Distribution of velocity and phases in cross section D:(a) distribution of velocity and streamline;(b) distribution of three phases
从图13(a)可以看出,4号阳极极距较大,旋流强度较大,析出的稀土液滴最终会向极距较小的一侧发生轻微的偏斜。比较图12(b)、图13(b),C截面中极距比为1.174,D截面中极距比为1.16,可得出随着极距比增大,稀土液滴的偏斜程度越大。因此在实际稀土电解过程中由于阳极极距不一致会导致析出金属发生偏斜,如果偏移程度过大可能会导致稀土液滴不易落入底部稀土收集槽中,造成稀土金属的浪费。
3.2.3 气泡流穿透深度
从阳极内表面产生的气泡流与阳极内壁面的距离即为气泡穿透深度。图14所示为不同高度横截面电解槽气泡-电解质相分布图。

图14 不同高度下电解槽截面气泡-电解质相分布图:(a) z=0.2 m;(b) z=0.61 mFig.14 Distributions of phases in cross sections of different heights:(a) z=0.2 m;(b) z=0.61 m
从图14可以看出,从阳极底部内壁面析出的气泡流几乎紧贴壁面向上流动,随着高度不断上升,气泡不断聚集,在顶部自由液面气泡流穿透深度达到最大,并最终在顶部自由液面逸出。非均一极距条件下,由于从阳极产生的气泡初始速度不同,使得气泡穿透深度发生改变,图15所示为均一极距与非均一极距的穿透深度。
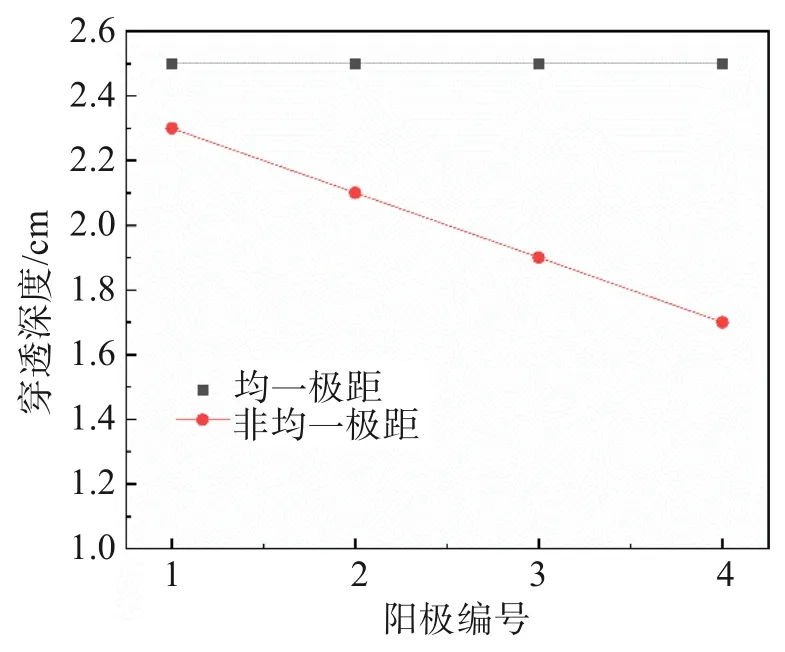
图15 气泡穿透深度Fig.15 Bubble penetration depth
从图15中可以看出,均一极距条件下4个阳极产生气泡流穿透深度相同,均为2.5 cm。而非均一极距条件下1—4号阳极产生的气泡流的穿透深度随着极距的增大不断减小。如果在气泡逸出区域加料,则尺寸较小的稀土氧化物颗粒会随着上升气流飘走而无法进入液相电解质,造成原料的浪费。因此在加料时应尽可能的选择极距较大区域。
4 结论
本文使用数值模拟方法计算了6 kA稀土钕电解槽气泡-电解质-稀土金属三相流动过程,分析了实际电解槽三相流动规律,主要结论如下:
1)建立了二维和三维电解槽几何模型并使用ANASY-FLUENT软件对模型进行求解。计算结果与相关文献研究结果基本一致。
2)模拟计算了二维和三维稀土电解槽几何模型的流场分布。对比发现二维模型无法模拟出阳极空隙处及阳极外侧的流动过程。三维模型能够模拟出完整、详细的电解槽内多相流动过程,能更加准确地反映实际电解槽电解内的流动特性。
3)根据实际工况建立了非均一极距几何模型。计算得出非均一极距条件下随着极距增大,主旋涡中心位置向着阴极和电解槽底部发生偏斜,尽管流速改变较小,但由于电解质旋流强度不同,导致稀土金属产生偏斜,且偏斜程度随着极距比的降低而减小。气泡流穿透深度随着极距的增大不断减小,在加料时应尽可能的选择极距较大区域以防原料的浪费。
