改进量子遗传算法在含分布式电源配电网中的应用
2023-11-17张雅婷郭亮郭达李乾刘保安
张雅婷,郭亮,郭达,李乾,刘保安
(1.国网太原供电公司,太原 030012; 2.国网石家庄供电公司,石家庄 050000)
0 引 言
配电网位于电力系统的末端,其供电可靠性和质量不仅关乎企业的经济效益,而且具有巨大的社会效益[1]。但随着人口的快速增长,供电系统面临越来越大的压力和频发的故障。这些障碍严重影响了电网的安全。据不完全统计,目前80%以上的停电是由配电系统故障引起的。这些故障严重影响了电网的安全[2],需加强电力系统安全分析,尤其是配电网故障分析和定位。
随着智能配电网技术的发展,国内外配电网的定位技术主要分为主动定位法和被动定位法。主动定位法通过向故障线注入检测信号实现故障定位,被动定位法根据传输线本身的电流和电压信号实现故障定位。在文献[3]中,提出了一种基于π型线的等效模型,并使用内部电阻电压源代替了并网分布式电源。考虑到过渡电阻不消耗无功功率,建立故障定位方程,并结合同步测量数据得到故障测距。在文献[4]中,提出了一种基于遗传算法的配电网故障定位方法,应用较为成熟,但算法局部搜索能力较差和后期搜索效率低。在文献[5]中,将粒子群优化算法和矩阵算法相结合,对配电网进行故障定位。该方法首先找到故障线,然后确定故障点的确切位置。在文献[6]中,提出一种结合粒子群优化算法和差分进化算法用于配电网的故障定位。该算法首先对二元系统的故障信息进行处理,然后利用两种群进化和信息交互机制共享最优解,实现配电网的精确定位。随着分布式电源的接入,配电网已从单向潮流变为双向潮流,从而降低了现有故障定位方法的准确性。因此,有必要研究一种具有高容错性和适用于含分布式的配电网络故障定位方法。
在此背景下,本文提出了一种用于配电网故障定位的改进量子遗传算法。使用基于梯度下降的动态门策略更新量子门,并使用Tent混沌优化方法跳出局部最优,通过仿真对该算法的准确性和有效性进行验证。
1 含DG配电网故障定位方法
随着配电网中分布式电源(distribute generation,DG)的接入越来越多,对其安全性提出了更高要求[7]。同时,也出现了新的问题,特别是潮流方向由单变双,使得某些故障定位方法无法应用[8]。在本文中,使用量子遗传算法(quantum genetic algorithm,QGA)对故障数据信息进行分析,定位故障区域。算法主要有开关编码、开关与馈线联络函数、目标函数三个方面。
1.1 编码方式
含分布式电源的配电网与传统配电网络之间的最大区别是双向流动问题。为了简化编码,如果在配电网馈线部分存在分布式电源,则定义从系统电源到分布式电源为正方向[9]。如果馈线部分中没有分布式电源,正方向为电源到负载方向,这里正方向仅用于编码,非实际功率方向。
如果每个开关节点配电开关监控终端(feeder terminal unit,FTU)检测的故障电流方向与定义正方向相匹配,则报告的状态信息为1。如果FTU检测到的故障电流穿越的方向与定义正方向不匹配,则报告的状态信息为-1。如果没有故障电流流过,则报告状态信息为0。表1所示分布式电源的开关编码模式。

表1 开关编码方式(含DG)
1.2 开关与馈线间的联络方式
在具有分布式电源的双向配电网中,线路在故障后,安装在线路上的FTU检测状态信息由原始0/1状态变为-1/0/1。因此,有必要建立一个适当的数学模型来反映开关和馈线之间的信息交互[10]。图1为简单配电网模型(含DG)。

图1 配电网模型(含DG)
当流过故障电流越线信息的方向与文中定义的正方向一致时,故障电流为正向,不一致为反向。从图1可以看出,开关S2在馈线L2、L3、L6、L7故障的情况下,S2的故障电流为正向,在馈线L1、L4、L5故障的情况下,S2的故障电流为反向。K1、K2为分布式电源的并网开关。
故障定位系统在至少一条馈线故障或FTU信息出错时开始运行[11]。开关与馈线之间的联络方式如式(1)和(2)所示。
(1)
xi+yj=m(i、j=1,2,3,……,m)
(2)
式(1)由两部分组成。下游馈线部分和上游馈线部分与下游分布式电源的乘积。在下游没有分布式电源的情况下,该部分为0,所有开关节点上、下游减法运算[12]。表2所示所有开关上游和下游馈线部分。

表2 开关节点和馈线关联
1.3 目标函数
上述方法改善了各开关的编码以及与馈线间的联络方式,能够正确反映与馈线间的关系,目标函数不受分布式电源影响[13]。目标函数如式(3)所示。
(3)
在式中,I(Sm)为第m个FTU传馈线状态信息,取值为-1/0/1;N为开关 总数;X(Se)为故障馈线数;w为防止误判权重系数,一般为0.5。如果FTU上传状态信息与期望的状态匹配,则目标函数Fmin取最优值。
2 改进算法
2.1 调整量子旋转门策略
QGA算法使用固定旋转角策略。本文改良为动态自适应角策略,大幅提高了算法的收敛速度[14]。旋转角在初期赋予较大的值,随着不断进化,使用梯度下降法逐渐减小旋转角。采用如下方法确定方向和大小。
1)量子旋转门的方向确定。
令α0和β0为某量子当前搜索的全局最优解的概率幅。α1和β1为相应量子位的当前解的概率幅,如式(4)所示。
(4)
然后根据以下规则选择旋转角度δ的方向:当δ≠0时,方向为-sgn(δ);当δ=0 时,当前方向可以为正或负。
2)量子旋转门大小确定。
采用梯度下降法优化旋转角度。当目标函数变化率较大时,减小旋转角步长,变化率较小时,增加旋转角步长。式(5)~式(7)所示[15]。
(5)

(6)

(7)
对于离散数据,梯度是相邻两代之间的一阶差,(0,μVSmax]如式(8)~式(10)所示。
(8)
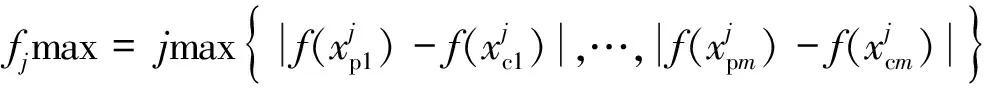
(9)
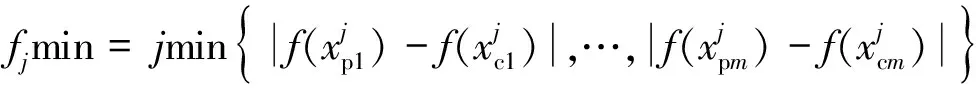
(10)

2.2 跳出局部最优解
离散度分析作为测量数据分布程度的方法,主要从数据集中程度和数据分散程度两个方面反映了数据变化的趋势[16]。如果为局部优化,则目标值趋于平稳,离散度小。因此,基于每个迭代过程,离散分析方法可以用于分析每个个体的目标值,并确定其是否是局部最优值。离散系数VS的上限VSmax,下限为0。即VS∈(0,VSmax]。如式(11)~式(13)所示。
(11)
(12)
(13)

VS接近0,种群目标值越集中,接近VSmax,种群越离散,设定阀值,μ在(0.01-0.5)取值。在每次迭代期间,如果VS值介于(0,μVSmax]之间,则种群陷入局部最优,必须优化扰动此代的种群。如果VS值介于(μVSmax,VSmax]之间,则种群的个体目标值被认为是非常离散的[17]。记录当前的扰动次数m,超过10次结束优化。
在QGA算法进化中引入了混沌优化思想。增加算法种群的多样性,从而跳出局部最优Tent映射是具有均匀概率密度、功率谱密度和理想相关性。表达式如式(14)所示[18]。
xn+1=a-1-a|xn|,a∈(1,2]
(14)
Tent映射的Lyapunov指数如式(15)所示。
(15)
当a≤1时,系统是稳定的。当a>1时,系统在无序状态[19]。当a=2时,这个系统在中心映射中。Tent映射在大数据序列处理中有很大的优势,但是由于迭代序列很短而且不稳定,因此必须引入随机方程方法以改善Tent映射。如式(16)所示,对序列xk施加扰动使其跳出小周期或固定点,使系统再次陷入混沌[20]。
(16)
改进的具体步骤如下。
1)步骤一:在迭代过程中,确定第j代种群陷入局部最优,取对应于最小和最大目标值的个体值pjminf和pjmaxf;
2)步骤二:使用向量空间中的欧氏距离dj作为混沌搜索半径rj的基础。欧几里德距离dj是pjminf和pjmaxf两个个体的向量值距离,如式(17)和(18)所示。
(17)
rj=γdj
(18)
在式中,γ为搜索半径的倍数;
3)步骤三:获取0到1之间的随机数x0,将映射表达式代入生成n×m维序列,将序列号乘以半径rj,得到新种群的扰动矩阵Δ;
4)步骤四:根据pjminf和pjmaxf个体值的均值pjbzse为基值,将扰动矩阵Δ的每一列向量与pjbzse叠加生成新种群;
5)步骤五:继续与新物种群迭代,混沌Tent映射良好的遍历性保证了扰动矩阵在搜索半径上的分布,提高了新种群的多样性和后续搜索的准确性。
2.3 改进算法流程
改进的量子遗传算法在配电网(含DG)中故障定位应用,步骤如下:

2)步骤二:将每个FTU上传开关的实际故障信息与目标函数结合起来,以测量组中每个单独染色体的目标值[21];
3)步骤三:记录最优目标值对应的个体染色体,作为下一代进化的基础;
4)步骤四:判断当前状态是否进入局部最优状态。如果进入,就跳出局部最优。如果没有,更新染色体得到新种群Qt+1{xi},记录最优个人及其目标价值;
5)步骤五:确定迭代是否结束。如果结束,输出结果。否则t=t+1,跳到步骤二。流程图如图2所示。

图2 IQGA算法流程图
3 实验结果与分析
3.1 仿真参数
在实际应用中,本文采用IEEE 69节点配电网模型(含DG)。IQGA算法用于配电网故障定位。仿真参数为最大进化代数100、种群大小80,使用改进的旋转角度策略,离散系数的区间阈值系数μ=0.03。模拟单重和多重故障。图3所示含分布式电源的IEEE 69节点配电网模型。

图3 含DG的IEEE 69配电网
在图3中,DG1、DG2、DG3、DG4、DG5表示分布式电源。K1、K2、K3、K4、K5是分布式电源并未开关,S1、S2、…、S69是配电网的各开关。L1、L2、…、L69为配电网中的馈线编号。假设每个开关都有FTU故障检测。为了避免意外结果,将“仿真数”设置为50。
3.2 单重故障分析
如图3所示,含分布式电源的IEEE-69节点配电网模型,通过仿真对单重故障进行了分析具体故障参数请参见表3。

表3 单重故障参数
从表3中可知,将分布式电源连接到电网,L9馈线发生单重故障且没有畸变失真,则算法的平均迭代次数为67.63,目标值为0.5。当L20馈线有单重故障,则平均迭代次数67.32,目标值1.5。当L48和L62馈线有双信息畸变单故障发生,则平均迭代次数为68.44和68.12,目标值都为2.5。图4所示L9馈线单重故障的仿真结果。

图4 L9馈线单重故障
3.3 多重故障分析
如图3所示,含分布式电源的IEEE 69节点配电网模型,通过仿真对多重故障进行了分析。具体故障参数见表4。

表4 多重故障参数
从表4中可知,将分布式电源并入到配电网时,L9,L31馈线发生多重故障,并且无信息畸变时。算法的平均迭代次数为68.67,目标值1.0。L20,L42馈线中有多重障碍并且单信息畸变时,则平均迭代次数为畸变2,目标值为2.0。图5所示L20,L42馈线的多重故障仿真结果。

图5 L20,L42馈线多重故障仿真结果
3.4 算法对比
为了对本文改进量子遗传算法在配电网故障定位中应用的优越性进行验证,对表4中的第四种情况使用标准遗传算法和标准QGA进行仿真比较,进化过程如图6所示。

图6 算法比较
从图6可以看出本文提出的改进算法收敛速度最快。在45代左右达到最优且波动小。QGA在78代左右找到最优解,而GA在100代尚未达到最优解,并且该算法波动性大且不稳定。因此,与传统QGA和经典遗传算法相比,该算法在解决配电网故障方面具有显着优势。
仿真结果表明,该算法具有较快的收敛速度和较强的寻优能力。最后,通过与遗传算法和QGA算法比较。该算法在识别配电网故障方面具有较大的优势。
4 结束语
针对含分布式电源的配电网故障定位问题,本文提出了一种改进的量子遗传算法,并通过仿真与改进前算法进行了比较,验证了该算法的准确性和有效性。结果表明,该方法可以快速有效地定位含分布式电源的配电网故障区段,具有较强的搜索能力和快速收敛性。由于当前实验室硬件要求和实验数据的规模,含分布式电源的配电网中故障定位研究仍处于早期阶段。在此基础上,下一步的工作重点将是逐步改进和完善。
