考虑可靠性成本的配电网多阶段扩展规划方法

2023-11-17张军达卢姬常俊晓廖小兵

电测与仪表 2023年11期

张军达,卢姬,常俊晓,廖小兵

(1.国网浙江综合能源服务有限公司,杭州 310016; 2.国网浙江台州供电公司,浙江台州 318000;3.武汉工程大学电气信息学院,武汉 430205)

0 引言

现有的供电中断90%以上是由配电系统引发的,因此,从配电网规划层面上考虑可靠性约束对提升供电可靠性至关重要[1-2]。在规划层面考虑可靠性约束是通过权衡投资成本与可靠性水平提升之间的关系来实现配电网最优扩展规划。这样一方面可以减少用户供电中断未提供电能而造成的损失;另一方面在供电可靠性较差的情况下减少相应的考核惩罚,即在供电可靠性较高时可以获得相应的考核奖励[3],而在供电可靠性较低时需要付出惩罚成本。

为了量化可靠性的经济效益,即可靠性价值,必须量化配电网的可靠性水平。为此,配电网采用了多种可靠性评估指标[4-5],其中系统平均停电持续时间指标(SAIDI),系统平均停电频率指标(SAIFI)和系统缺供电量期望(EENS)这三类指标使用最多[6]。SAIDI,SAIFI和EENS这三类指标通常使用模拟法去逐个分析每个故障事件对系统和用户停电的影响,逐个模拟所有元件故障的影响,这种方法一方面耗时,另一方面无法实现可靠性指标的显式表达,即建立元件故障参数与可靠性指标之间的显式关系[7]。这也是基于模拟法的可靠性指标难以嵌入到配电网扩展规划模型中的重要原因,因此,已有文献采用迭代方法,即先假设网络拓扑结构已知,然后校验可靠性指标,进而改进配电网规划。主要是采用启发式的智能优化算法,比如文献[8]中的遗传算法,文献[9]中的非支配排序遗传算法等。然而,采用启发式算法求解考虑可靠性约束的配电网扩展规划模型,难以保证规划模型的收敛性和最优性,会造成一定的经济性或可靠性损失。

为了克服模拟法评估可靠性的弊端,基于解析法的配电网可靠性评估方法应运而生。文献[10]基于节点相关信息的等值递推关系,提出了代数模型的可靠性指标计算方法;文献[11]采用层次聚类方法对典型馈线进行识别和聚类,通过回归分析导出了每种典型馈线拓扑下可靠性指标的显式公式。文献[12]建立了基于拓扑变量的混合整数线性优化模型的可靠性指标评估方法。这些非模拟法的配电网可靠性评估方法从根本上避免了多次模拟的思路。在此基础上,文献[13]将影响可靠性的网络拓扑转化为优化模型,建立了同时考虑经济性和可靠性的配电网多阶段扩展规划的混合整数线性优化模型。文献[14]将面向可靠性的成本纳入到配电网扩展规划模型中,建立了一组混合整数线性方程来计算最常见的配电网可靠性指标。文献[15]通过将可靠性指标计算过程解析化,并嵌入到配电网扩展规划模型中,可以精确考虑故障隔离、负荷转供和恢复策略,基于线性化潮流,该配电网扩展规划模型是一个混合整数线性优化问题,可以高效求解。文献[16]建立了交直流混合配电网的可靠性显式表达模型,提出了一种考虑可靠性成本的交直流混合配电网混合整数线性规划模型。然后,这些文献对可靠性成本的建模均不够全面,要么以系统缺供电量期望造成的损失作为可靠性成本,缺少对系统平均停电持续时间指标和系统平均停电频率指标的考虑。

在此基础上,文中提出了考虑可靠性成本的配电网多阶段扩展规划方法。首先在可靠性成本方面,不仅考虑了系统缺供电量造成的收入损失,而且基于可靠性激励率,建立了系统平均停电频率指标和系统平均停电持续时间指标的相关可靠性成本,其次,采用图论知识建立了显式的可靠性指标评估模型,最后形成了考虑可靠性成本的配电网多阶段扩展规划的混合整数线性优化模型,适用于商业求解器求解。在四个算例系统上的仿真结果验证了本文所提出方法的有效性和扩展性。

1 可靠性约束的配电网扩展规划模型

传统的配电网扩展规划的目标是使得变电站和馈线的投资成本、系统运行成本最小化,以满足不断增长的负荷需求[17-18]。而考虑可靠性约束配电网可靠性评估依赖于以下假设:

1)仅考虑由于单条支路停电而导致的持续停电,影响支路停电的特征量是故障率和停电持续时间;

2)考虑三相平衡的辐射状或网状配电网,其中连接到变电站的每条支路都配备了断路器,在变电站的输出端没有重合闸。此外,所有支路都配备了一个开关,以进行故障隔离,即隔离故障下游部分,以满足非故障部分的负荷需求。因此,一旦发生持续故障,故障上游的第一个断路器就会跳闸,从而减少了所有下游负荷需求。随后,通过操作开关和断路器重构网络拓扑,以减少停电负荷。为此,打开故障上游的第一个开关以隔离故障,然后关闭断路器,以便恢复断路器和开关之间所有负荷的电源。最后,一旦隔离故障被清除,相应的开关闭合,并重新恢复供电。

因此,负荷节点受到两种类型停电的影响:修复和切换停电,在修复损坏之前不会恢复供电;仅切换停电,这与为清除故障组件而实施的网络重构有关。

图1给出了所提出的可靠性约束的配电网扩展规划方法流程图,通过线性化的潮流模型,建立的可靠性约束的配电网扩展规划模型是一个混合整数线性优化模型,可以通过商业求解器直接求解。

1.1 目标函数

建立的可靠性约束的配电网多阶段扩展规划的目标是最小化系统总成本,包括投资成本,运行成本以及可靠性成本,如式(1)所示:

(1)

式中t为规划阶段;T为规划阶段总数;r为利率;Invt,Opt分别为t阶段的投资成本和运行成本;RRCt为t阶段的可靠性成本。

t阶段的投资成本包括新建馈线、更换现有馈线、建造或扩建变电站以及增加变电站变压器的投资成本,如式(2)所示:

(2)

式中l为馈线索引;k为方案编号;LN为新增的馈线集合;Kl为馈线l的投资方案集合;rrk为方案k的资本回收率;CCl,k为馈线l方案k的施工成本系数;xl,k,t为t阶段馈线l投资方案k的0-1决策变量;RCl,k为馈线l方案k的更换成本系数;n为节点编号;ΩS为变电站节点集合;rrn为节点n处变电站中除变压器以外的资本回收率;ECn为节点n处新变电站建设成本系数或现有变电站扩建成本系数;ICn,k为节点n处变电站变压器方案k的投资系数;xn,t为阶段t节点n处新建变电站或扩建变电站的0-1决策变量;xn,k,t为阶段t节点n处变电所变压器方案k的0-1决策变量。

其中资本回收率定义为rrk=r(1+r)ULk/[(1+r)ULk-1],∀k∈Kl∪Kn,ULk为方案k使用寿命和rrn=r(1+r)ULn/[(1+r)ULn-1],∀n∈ΩS,ULn为节点n处变电站中除变压器以外的设备使用寿命。

t阶段的运行成本包括馈线的运行成本、变电站变压器的维护成本以及变电站的电力成本,如式(3)所示:

(3)

式中LF、LR分别为现有的馈线集合、现有的可更换馈线集合;OCl为现有馈线l的运行成本系数;yl,t为t阶段是否使用现有馈线l的0-1决策变量;OCl,k为馈线l方案k的运行成本系数;yl,k,t为t阶段馈线l的方案k是否使用的0-1决策变量;Kn为节点n处变电站变压器的投资方案;MCn,k为节点n处变电站变压器方案k的维护成本系数;τ表示阶段;b为负荷持续时间曲线分块的索引;LD为负荷持续时间曲线的分块集合;pf表示系统功率因数;Δb为负荷块b的持续时间;Prn,b,t为在阶段t节点n处负荷块b的电价;gn,b,t表示节在t阶段点n处变电站的负荷块b注入电力。

最后,t阶段的可靠性相关成本基于以下因素建模:在网络故障期间未向负荷提供电能而造成的电费损失;可靠性指标的激励成本,如式(4)所示:

(4)

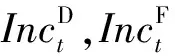
其中预期电费损失RLt为:

RLt=ERtEENSt∀t∈T

(5)

式中ERt为t阶段的每单位电能的预期收益;EENSt为在t阶段未提供的预期电量。

与可靠性指标相关的激励成本采用式(6)～式(7)计算:

(6)

(7)

式(6)～式(7)分别基于系统平均停电持续时间指标和系统平均停电次数指标进行线性激励来建立可靠性成本模型。因此,当可靠性指标小于相应的基准值,即产生奖励效益,否则为惩罚成本。

1.2 投资0-1决策变量约束

投资决策受以下约束:

(8)

(9)

(10)

(11)

xl,k,t∈{0,1} ∀l∈LR∪LN,∀k∈Kl,∀t∈T

(12)

xn,t∈{0,1} ∀n∈ΩS,∀t∈T

(13)

xn,k,t∈{0,1} ∀n∈ΩS,∀k∈Kn,∀t∈T

(14)

式(8)～式(10)规定了在规划期内,只允许进行一项投资。式(11)是为了防止在相应变电站扩建之前安装新的变电站变压器。

对馈线利用变量约束为式(15)～式(21):

yl,t=1; ∀l∈LFLSW,∀t∈T

(15)

(16)

(17)

(18)

(19)

yl,t∈{0,1}; ∀l∈LF∪LR,∀t∈T

(20)

yl,k,t∈{0,1}; ∀l∈LR∪LN,∀k∈Kl,∀t∈T

(21)

式中LSW表示节点集合L中包含正常运行下可切换的馈线集合。

式(15)～式(17)通过馈线利用变量设置在正常运行下不可切换状态,因此不能用于网络重构;现有的不可切换馈线在所有阶段都可用,因此它们的利用率变量必须等于1,如式(15)所示。在进行任何更换操作之前,必须使用现有的可更换馈线部分,如式(16)所示。最后,根据式(17)的规定,从进行相应投资的阶段开始,必须使用可更换和新增馈线。

与式(16)和式(17)类似,式(18)和式(19)通过可更换和新增馈线利用变量设置为可切换状态,因此可用于网络重构。这些约束通过将馈线利用变量设置为0来避免使用网络中未安装的馈线部分选项。另一方面,对于已安装的选项,式(18)～式(19)对馈线利用变量没有限制,因此这些选项可用于优化网络的配置。

1.3 系统运行约束

系统运行受到式(22)～式(29)中定义的各种约束:

(22)

(23)

M(1-yl,t); ∀l∈LF∪LR,∀b∈LD,∀t∈T

(24)

(25)

(26)

(27)

(28)

(29)

采用文献[19]中线性化潮流模型,负荷节点和变电站节点的功率平衡分别由式(22)～式(23)确定。式(24)～式(25)对各种类型的支路潮流进行建模。式(26)～式(28)分别对现有和新增馈线的变电站注入功率和流过的有功功率流施加了限制。节点电压的下限和上限在式(29)中约束。

1.4 辐射状拓扑约束

本小节利用图论[20]知识在配电网扩展规划模型中施加辐射状拓扑约束。根据图论知识,如果节点数等于支路数加1,则连接图没有环路,这一结论可以扩展到一个图,该图由没有环路的连接子图不相交联合组成,其节点数等于支路数加上子图数。首先,在每个阶段,可能会隔离多个节点,因此不应计算在内;其次,网络的子图数量等于现有变电站的数量,因为每组连接的负荷节点必须由单个变电站供电。根据图论这一结论,现有馈线的数量等于连接节点的数量(即连接的负荷节点数加上连接的变电站节点的数量)减去子图的数量。由于连接的变电站节点数等于子图的数量,如果在运行的馈线的数量等于连接的负荷节点的数量,则可以确保辐射状运行。

这种基于图论的辐射状拓扑约束如式(30)～式(36)所示:

ul,t=yl,t; ∀l∈LF,∀t∈T

(30)

(31)

(32)

0≤ul,t≤M|dl,t|; ∀l∈L,∀t∈T

(33)

ul,t≤LPMn,t;∀n∈ΩD, ∀l∈L|χn,l≠0|,∀t∈T

(34)

LPMn,t≤1; ∀n∈ΩD,∀t∈T

(35)

(36)

式中dl,t为在阶段t馈线l下游的平均负荷需求;L为所有馈线集合;ΩD为负荷节点集合;LPMn,t是一个0-1变量,如果节点n在阶段t至少连接到一个馈线,则等于1,否则为0;ul,t是一个0-1变量,如果t阶段馈线l在运行,t等于1,否则为0。

式(30)～式(32)分别为现有的固定馈线、现有的可更换馈线和新的馈线建立的ul,t模型。根据式(33),对于未使用的馈线,变量ul,t设为0。式(33)中,dl,t为t阶段通过馈线l的平均负荷需求,由于缺乏对网络拓扑的预知,因此使用绝对值。对于非隔离节点,即对于与之连接的至少一个支路的利用变量ul,t为1的节点,根据式(34)～式(35)将LPMn,t设为1。另一方面,对于那些没有任何连接的支路处于运行状态的节点,式(34)～式(36)将LPMn,t设为0。对于此类节点,式(34)～式(35)确保LPMn,t取小于或等于1的非负值。最后,式(36)考虑到无环路连通图的支路数最少,则只有在每个孤立节点LPMn,t等于0的情况下才能满足式(36)。

2 显式可靠性指标计算方法

本节阐述如何显式计算三类常用的配电网可靠性指标,即系统缺供电量期望,系统平均停电持续时间指标和系统平均停电次数指标。与已有文献相比,文中所提出的显式可靠性指标计算方法具有以下三个特点:1)通过额外的二进制变量和新的非线性表达式考虑了网络资产的投资决策;2)通过在虚构系统上施加KCL来表征变电站可用性;3)可靠性指标的混合整数非线性表达式的等效线性化。

2.1 EENS

EENS量化了由于网络故障而未提供的期望电量,可以表示为由于每个馈线部分故障而减少的供电量的总和,如式(37)所示:

(37)

式中BEENSl,t为在阶段t馈线l的未提供预期电量。

(38)

对于现有的可更换和新添加的馈线段部分,每个选项k的故障率和维修时间各不相同。因此,在式(39)和式(40)中分别使用二进制利用率变量来表征可更换和新添加的馈线部分的可靠性参数:

(39)

∀l∈LN,∀t∈T

(40)

为了得到每个馈线下游的总负荷需求,即dl,t,将KCL应用于一个虚构的相同拓扑结构的无损网络,其节点负荷等于年平均节点负荷需求,如式(41)～式(44)所示:

(41)

(42)

-Mul,t≤dl,t≤Mul,t; ∀l∈L,∀t∈T

(43)

(44)

式(41)～式(42)分别建立了虚拟网络负荷节点和变电站节点的功率平衡方程。式(43)～式(44)将未利用馈线的虚拟功率和未利用变电站的虚拟电量均设为0。

(45)

(46)

(47)

(48)

δl,t=0; ∀l∈SL,∀t∈T

(49)

为了说明式(41)～式(49)的过程,以图2所示的简单网状结构表示给定时间阶段t的投资计划。可以看出,该网络有两个变电站节点,三个平均负荷需求都等于1 MW的负荷节点,以及六个馈线,其中三个直接连接到变电站节点,因此,L={l1-l6}和SL={l1,l4,l5}。图2还显示了两种可能的辐射状网络拓扑,称为辐射状拓扑1和辐射状拓扑2。如图2所示,每个馈线的第一个馈线部分甚至馈线的数量都依赖于拓扑结构。

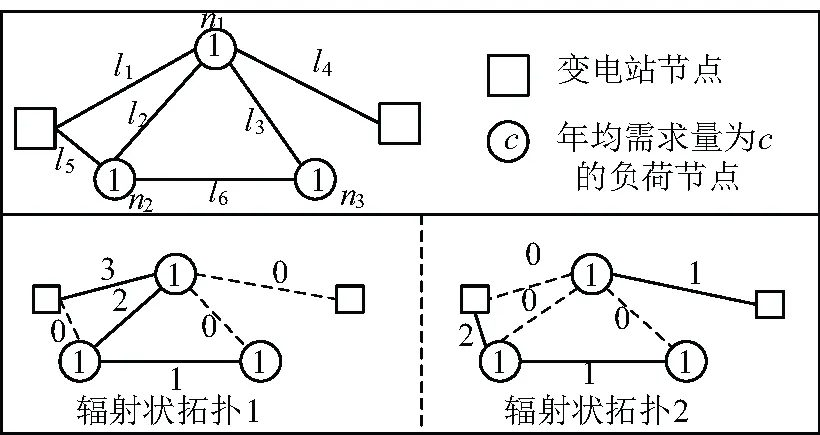
图2 两种可能的辐射状拓扑的馈线虚拟功率

对于图2中的两种辐射状拓扑,虚构功率dl,t由式(41)～式(44)得到的结果显示在相应的馈线旁边。可以看出,每个馈线的第一馈线部分的虚拟功率等于该馈线的总负荷需求。

δl6,t=zl6,l1,t(|dl1,t|-|dl6,t|)+zl6,l4,t(|dl4,t|-|dl6,t|)+zl6,l5,t

(|dl5,t|-|dl6,t|)=1×(3-1)+0×(0-1)+0×(3-1)=2

这等于馈线l6上游的总负荷需求。类似地,对于辐射状拓扑2中的馈线zl6,l5,t=1和zl6,l1,t=zl6,l4,t=0,因此,由式(48)可得:

δl6,t=zl6,l1,t(|dl1,t|-|dl6,t|)+zl6,l4,t(|dl4,t|-|dl6,t|)+zl6,l5,t

(|dl5,t|-|dl6,t|)=0×(0-1)+0×(0-1)+1×(2-1)=1

(50)

(51)

(52)

此外,式(39)线性化为:

M(1-yl,t); ∀l∈LR,∀t∈T

(53)

M(1-yl,k,t); ∀l∈LR,∀k∈Kl,∀t∈T

(54)

-M(1-yl,k,t); ∀l∈LR,∀k∈Kl,∀t∈T

(55)

式(53)～式(54)当yl,t=0和yl,k,t=0失效,因为式(53)～式(54)的右侧变为较大的负值。因此,根据式(55),BEENSl,t的下限为0。相反,当yl,t=1和yl,k,t=1,式(53)和式(54)分别将BEENSl,t的下界设置在式(39)的右边。

同理,式(40)和式(48)线性化为:

(56)

(57)

2.2 SAIDI

SAIDI表征配电网用户的平均年停电持续时间。馈线l在阶段t故障引起的全年用户停电总时间表示为BIDIl,t,SAIDI指标可以表示为:

(58)

式中BIDIl,t为在阶段t馈线l故障导致停电户中断时间;Nn,t为在阶段t连接到节点n的用户数。

式(59)～式(61)的模型BIDIl,t适用于各种类型的馈段。这些表达式分别与式(38)～式(40)相同,其中hl,t和ηl,t分别起到dl,t和δl,t的作用。

∀l∈LF,∀t∈T

(59)

(60)

∀l∈LN,∀t∈T

(61)

式中ηl,t为t阶段连接到馈线l的上游节点的用户数量;hl,t为t阶段馈线l下游节点连接的用户数。

为了获得hl,t,即t阶段馈线下游节点连接的用户数,将KCL应用于一个虚构的相同拓扑的无损网络,其节点负荷需求等于连接的用户数,如式(62)～式(65)所示:

(62)

(63)

-Mul,t≤hl,t≤Mul,t; ∀l∈L,∀t∈T

(64)

(65)

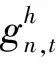
最后,与式(48)～式(49)类似,在t阶段连接到馈线l上游节点的用户数量ηl,t表示为:

(66)

ηl,t=0; ∀l∈SL,∀t∈T

(67)

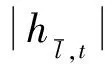
2.3 SAIFI

SAIFI指标表征配电网用户每年的平均停电次数。由于SAIFI与SAIDI的结构相似,其模型可以很容易地推导出,如下所示:

(68)

BIFIl,t=αlλl(|hl,t|+ηl,t); ∀l∈LF,∀t∈T

(69)

(70)

∀l∈LN,∀t∈T

(71)

式中BIFIl,t为在阶段t馈线l故障导致的用户停电次数;λl,k为馈线l方案k的单位长度的故障率。

式(68)～式(71)分别类似于式(58)～式(61),其中BIFIl,t与BIDIl,t类似。采用上述线性化方法同样可以式(68)～式(71)等效线性化。

3 算例分析

采用24节点、54节点、86节点和138节点四个算例系统来验证所提出的配电网扩展规划模型的有效性,详细数据见附录链接:https://pan.baidu.com/s/11B0_g7WUJsp3TKtnPLJnqw pwd=by4x,提取码:by4x。其中可靠性SAIDI和SAIFI的激励率分别为0.5和0.15,基准值分别为3.5和1;在Matlab2019Rb下调用CPLEX 12.6求解混合整数线性规划模型。在24节点和54节点算例系统中,最优间隙设置为e-7,在86节点和138节点算例系统中,最优间隙设置为e-2,这确保了在获得高质量近似最优解的同时保证算法的收敛。

3.1 24节点系统

24节点系统包括了20个负荷节点、4个变电站节点和33条馈线,其中2条是现有的固定馈线,2条是现有的可更换馈线,29条是候选的待建馈线。在测试中考虑了四类馈线投资方案和两种变电站变压器投资方案,规划周期分为三个阶段,所有馈线都是可切换的。

表1给出了采用传统迭代法和本文所提出的方法的24节点系统规划结果。其中,传统迭代法是在规划结果出来后进行验证可靠性得出的可靠性相关成本和和总成本。从表1中可以看出,与投资成本和运行成本相比,由于未提供的电能而造成的收入损失可以忽略不计。因此,这种收入损失本身并没有为配电网提供足够的动力来提高系统可靠性。因此,对于传统迭代法,规划周期内可靠性指标的平均值较高,可靠性水平较低。

表1 24节点系统规划结果

对于所提出的考虑可靠性成本的配电网扩展规划模型,可靠性激励增加了对网络资产的投资,以产生更可靠的网络。因此,由此可靠性指标得到了显著改善。值得一提的是,基于SAIDI和SAIFI的可靠性成本的负值反映了配电网可靠性指标低于相应基准值而获得的奖励。因此,与传统的迭代法相比,本文所提出的考虑可靠性成本的配电网扩展规划模型的总成本降低了3.47%。

图3和图4分别描绘出了传统迭代法和本文方法在规划周期第三阶段生成的网络拓扑。图3～图4中还显示了投资决策的类型和时间。除了与投资成本和运行成本相关的拓扑差异外,从图3～图4中可以看出,传统迭代法采用候选项A1和A2,而本文所提出的考虑可靠性成本的配电网扩展规划模型采用更可靠但更昂贵的候选方案A3和A4。

图3 24节点系统最后阶段的拓扑结构(传统迭代法)

图4 24节点系统最后阶段的拓扑结构(本文所提出的方法)

为了分析可靠性激励对考虑可靠性成本的配电网规划结果的影响,进一步总结了不同激励率下配电网可靠性指标、各项成本的变化情况。为此,假设系统平均停电持续时间指标和系统平均停电次数指标的激励率乘以0～2之间的比例因子,步长为0.5。图5显示了系统平均停电持续时间指标、系统平均停电频率指标和系统缺供电量期望值随激励率的变化情况。图6显示了两种可靠性激励方的净奖励的最终值、投资成本和运营成本的增加量,以及总成本增量随激励率的变化情况。如图5所示,随着激励率的增大,配电网可靠性指标下降,供电可靠性提升。然而,从图6中不难发现,只有相对较小的激励率投资才能提升可靠性,这是由于可靠性提升的增量成本低于增量收益。

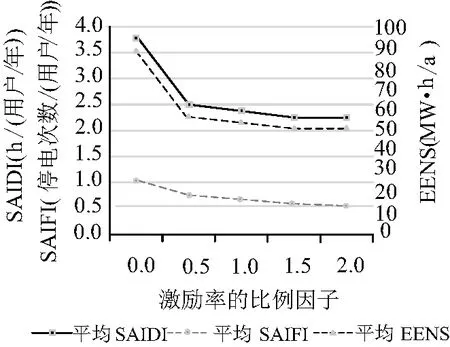
图5 不同激励率对可靠性指标的影响

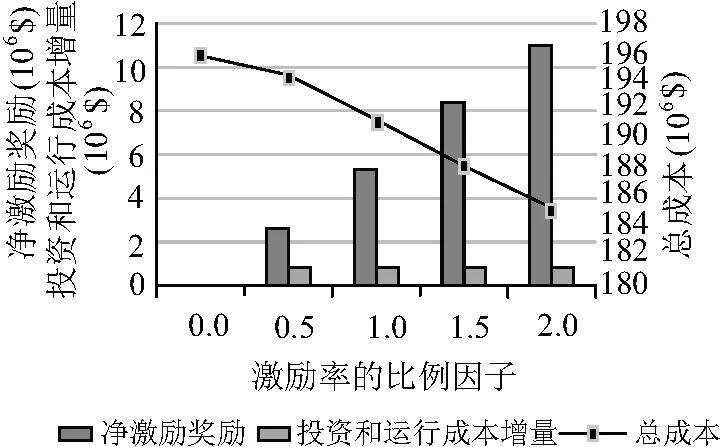
图6 不同激励率对系统各项成本的影响

3.2 54、86和138节点算例系统

为了分析所提方法的适用性,进一步在54节点、86节点和138节点三个较大的算例系统上进行仿真分析。54节点系统由50个负荷节点,4个变电站节点和63条馈线组成,包括9个现有的固定馈线,8条现有的可更换和46条候选馈线。86节点系统和138节点系统均由3个变电站节点组成,86节点系统通过94条馈线提供83个负荷节点,138节点系统有135个负荷节点和151条馈线。三个算例系统规划都考虑十个阶段。

表2给出了54、86、138节点系统规划结果。应当指出,基于系统平均停电持续时间指标和系统平均停电频率指标的可靠性成本的正值表明可靠性指标比基准值差,因此受到了处罚。另一方面,这些可靠性成本负值,例如86节点和138节点系统,通过达到低于(优于)相应基准的可靠性指标而获得的奖励。同样,由于三个算例系统未向用户提供电能而造成的收入损失相对而言微不足道,这表明该可靠性指标不能充分激励可靠性提升的投资。这一结果证明了可靠性激励在保证配电网可靠性水平方面的重要意义,而不是单纯的考虑未向用户提供电能而造成的收入损失。