双转台五轴机床旋转轴位置无关几何误差的辨识

梁小冰 卢耀安 王成勇

1.广东工业大学机电工程学院,广州,5100062.广东工业大学广东省微创手术器械设计与精密制造重点实验室,广州,5100063.高性能工具全国重点实验室,广州,510006

0 引言

机床的空间误差主要是准静态误差和动态误差[1]。准静态误差来源主要包括几何误差/运动学误差、热误差、力致变形误差,动态误差主要由控制误差引起。准静态误差大约占机床总空间误差的70%[2]。几何误差是决定机床准静态精度的重要因素。相对于平动轴,五轴数控机床旋转轴的几何误差对机床精度影响更大[2-3]。

旋转轴几何误差主要分为位置无关几何误差(position-independent geometric errors,PIGEs)和位置相关几何误差(position-dependent geometric errors,PDGEs)[3-4]。PIGEs由机床各轴系之间的装配误差引起,PDGEs由机床轴自身所带缺陷引起。相较于PDGEs,PIGEs在五轴机床几何误差中所占比例较高,故旋转轴的PIGEs是影响五轴数控机床精度的主要因素[5]。

目前,无法采用仪器直接测量五轴机床旋转轴PIGEs,因此需要先建立机床几何误差模型来描述几何误差与仪器测量数据的关系;然后,基于小角度误差假设,在忽略二次项与高次项后,建立线性化的几何误差模型;最后,将仪器测量结果代入几何误差模型,通过求解线性方程组获得旋转轴的PIGEs。基于小角度误差假设和忽略二次项与高次项来简化机床的几何误差模型会影响机床几何误差的辨识精度。目前,建立机床旋转轴PIGEs模型的方法主要有齐次坐标变换法、螺旋理论法和对偶四元数法。侯宏天[6]采用齐次坐标变换原理建立了BC型五轴机床的几何误差模型和运动学模型,基于球杆仪(double ball bar,DBB)设计了平动轴与旋转轴的几何误差辨识方法,辨识了平动轴的21项几何误差和旋转轴的8项PIGEs。郭世杰等[7]基于齐次坐标变换方法建立了摆头-转台型五轴机床的PIGEs模型,利用球杆仪的4种测量模式辨识旋转轴的PIGEs。张童童[8]基于螺旋理论建立了五轴机床的几何误差模型,利用球杆仪设计了6种测量模式,实现了两旋转轴几何误差的辨识。XIANG等[9]基于螺旋理论构建了五轴机床几何误差模型,利用球杆仪实现了旋转轴12项PDGEs和8项PIGEs的解耦辨识。WANG等[10]基于对偶四元数建立了五轴机床的运动误差模型,通过双旋转轴联动驱动球杆仪运动,实现了两旋转轴的PIGEs辨识。

TSUTSUMI等[11]提出了经典的球杆仪轴向、径向测量模式,以及基于小角度误差假设的旋转轴PIGEs辨识方法。WANG等[12]提出了一种辨识旋转轴8项PIGEs的新方法,该方法不需要计算球杆仪长度变化曲线的圆心偏移量,而是将某些特殊位置处的球杆仪测试数据代入辨识模型,从而得到PIGEs。上述两种方法需要分步解耦辨识旋转轴误差,若旋转轴某项PIGE的辨识结果存在误差,则会累积传递给其他误差项,导致未能准确辨识旋转轴PIGEs。姚思涵[13]提出了使用球杆仪同步辨识旋转轴与平动轴PIGEs的方法,但该方法需要编程计算单旋转轴与单平动轴联动的球杆仪测量轨迹。XIA等[14]提出的一种基于球杆仪的旋转轴几何误差解耦辨识方法需要选择合适的球杆仪安装位置和方向。

双转台型五轴机床被广泛使用,因此本文以AC双转台型五轴机床为对象,研究机床旋转轴PIGEs辨识方法。目前,大多数旋转轴PIGEs辨识方法要么需要小角度误差假设和忽略二次项与高次项,要么需要分步解耦辨识。这些方法都会影响辨识精度,因此,本文提出一种基于差分演化算法的旋转轴PIGEs辨识方法。首先,基于球杆仪轴向、径向的测量方式建立机床旋转轴PIGEs与球杆仪长度变化的关系模型。其次,使用TSUTSUMI等[11]提出的误差辨识方法获得旋转轴PIGEs的初始解,然后使用差分演化算法实现旋转轴8项PIGEs的整体优化求解。最后,通过实验验证提出的误差辨识方法的有效性。

1 五轴机床旋转轴PIGEs辨识

1.1 基于球杆仪的PIGEs辨识方法

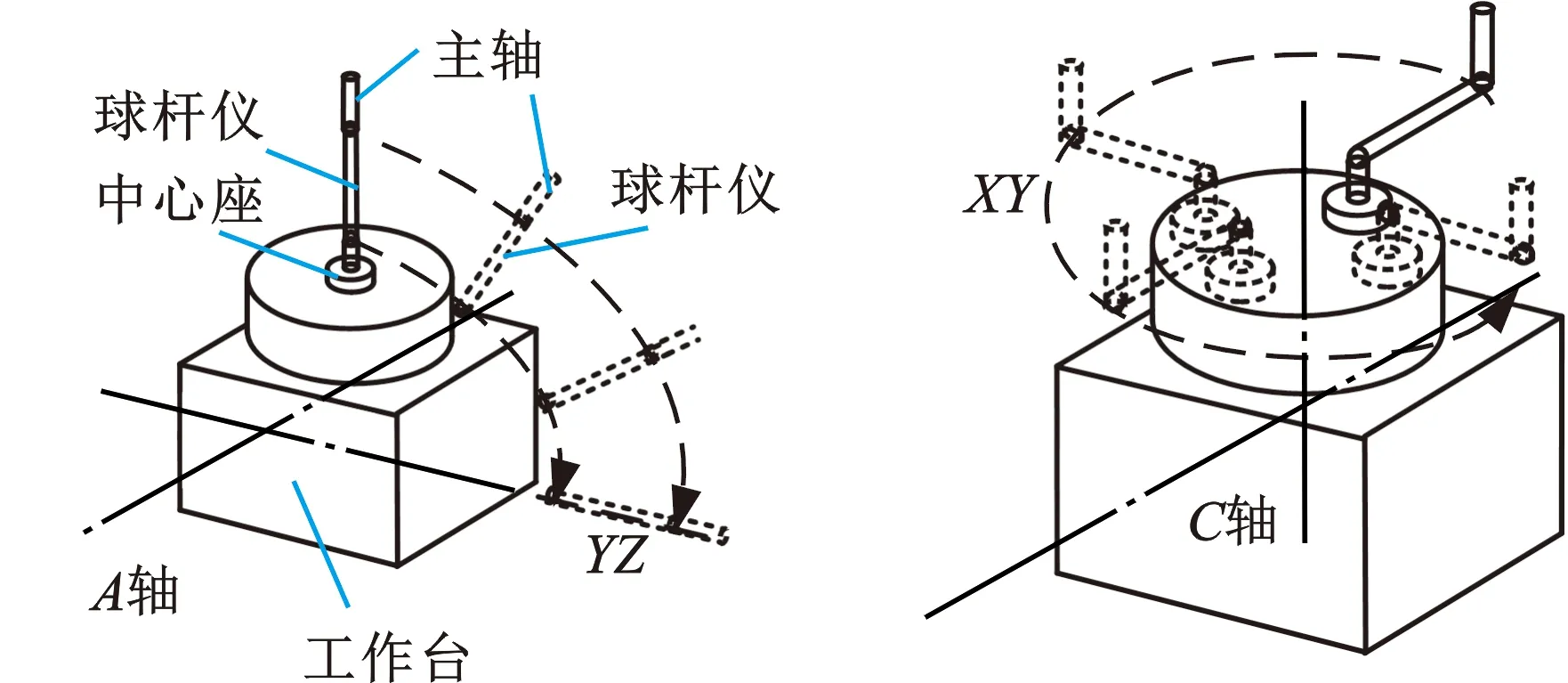
本文以AC双转台型五轴机床为研究对象,采用相对表示法定义旋转轴的PIGEs(图1),其中,OCXCYCZC为C轴坐标系,OAXAYAZA为A轴坐标系,OMXMYMZM为机床坐标系。δxAY、δyAY、δzAY分别为A轴坐标系原点在X、Y、Z方向的位移误差,αAY、βAY、γAY分别为A轴坐标系各轴关于X、Y、Z轴的角度误差,βCA为C轴坐标系相对于A轴坐标系的角度误差,δyCA为C轴坐标系原点相对于A轴坐标系原点在Y方向的位移误差。

图1 相对表示法定义旋转轴PIGEs

TSUTSUMI等[11]利用球杆仪对杆长方向长度变化最敏感的特征,提出了经典的球杆仪径向和轴向测量模式,以及机床旋转轴PIGEs辨识方法。测量AC双转台型五轴机床的A轴和C轴的PIGEs时,径向测量模式下,球杆仪杆长方向始终为圆轨迹的径向(图2a、图2b);轴向测量模式下,球杆仪杆长方向始终为测量轴的轴向(图2c、图2d)。利用球杆仪测量A轴PIGEs的过程中,机床的C轴和X轴保持静止,Y轴、Z轴与A轴联动进行圆周插补。利用球杆仪测量C轴PIGEs的过程中,机床的A轴和Z轴保持静止,X轴、Y轴与C轴联动进行圆周插补。

(a)A轴径向 (b)C轴径向

坐标系OMXMYMZM下,球杆仪主轴端接触球的球心坐标的计算表达式为

(1)

式中,φ为A轴旋转角度;θ为C轴旋转角度;[xSySzS]T为球杆仪主轴端接触球球心在旋转轴运动前的初始坐标。

球杆仪旋转工作台端接触球的球心坐标的计算表达式为

(2)

式中,[XTCYTCZTC]T为球杆仪旋转工作台端接触球球心在旋转轴运动前的初始坐标。

于是,球杆仪长度变化ΔL可通过下式获得

(3)

式中,L为球杆仪的公称杆长。

TSUTSUMI等[11]提出的旋转轴PIGEs辨识方法需要使用圆拟合球杆仪测量数据,然后根据旋转轴PIGEs与圆心偏移量之间的关系分步解耦辨识误差。本文采用最小二乘圆拟合方法——Pratt方法拟合球杆仪测量数据,获得其圆心坐标。拟合圆之前,需要对球杆仪测量数据进行预处理,将极坐标系表示的杆长变化量通过下式转化为直角坐标系表示:

(4)

式中,φi为第i个旋转轴角度;ΔLi为φi对应的球杆仪杆长变化量;ΔLmin为球杆仪杆长变化量的最小值。

TSUTSUMI等[11]提出的旋转轴PIGEs辨识步骤如下:

(1)球杆仪径向测量模式下,拟合A轴的测量数据,获得圆心偏移量δxAY、δyAY：

(5)

式中,ez、ey分别为拟合圆圆心在Z向和Y向的偏移量。

(2)球杆仪轴向测量模式下,拟合A轴的测量数据,获得圆心偏移量。仅存在βAY、γAY误差时,通过下式辨识βAY、γAY：

(6)

(3)球杆仪轴向测量模式下,拟合C轴的测量数据,获得圆心偏移量。仅存在αAY、βCA、βAY误差时,通过下式辨识角度误差:

(7)

式中,ex为拟合圆圆心在X向的偏移量;RB为球杆仪工作台端的接触球球心与C轴回转轴线在X方向的距离。

(4)球杆仪径向测量模式下,拟合C轴的测量数据,获得圆心偏移量,通过下式辨识角度误差:

(8)

1.2 基于差分演化算法的PIGEs辨识

TSUTSUMI等[11]基于小角度误差假设提出的旋转轴PIGEs辨识方法影响误差辨识的准确性,且该辨识方法需要分步解耦辨识误差,如果某项PIGEs的辨识结果存在偏差,则会累积传递给其他误差项。本文使用TSUTSUMI等[11]提出的辨识方法即通过式(5)～式(8)获得PIGEs初始解S,然后基于差分演化算法整体优化求解8项PIGEs,获得准确性更高的PIGEs。基于差分演化算法的旋转轴PIGEs辨识流程如图3所示,步骤如下:

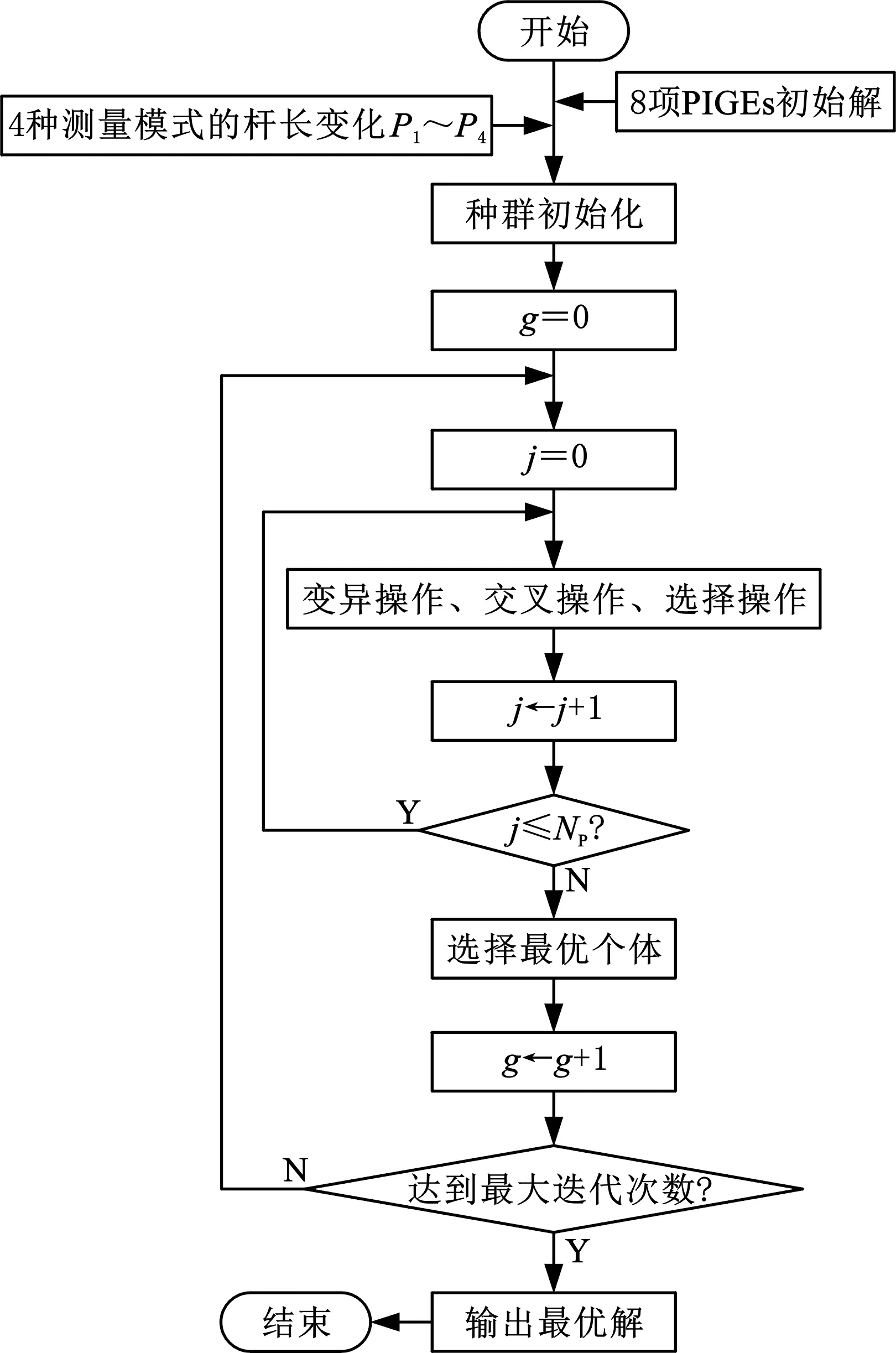
图3 基于差分演化算法的PIGEs辨识流程图

(1)初始化。种群内第j个个体的第i项位置无关几何误差为

Xj,i=(2Mj,i-1)(XU,i-XL,i)+Si

(9)

其中,Mj,i为在(0,1)的随机数,i=1,2,…,D;j=1,2,…,NP;D为变量维数,旋转轴存在8项PIGEs,即D=8;NP为种群数量,NP在5D～10D的优化结果较好[15];XU、XL分别为项误差的上限和下限,根据初始解的角度误差和位置误差适当取值;Si为初始解S的第i项PIGEs。

(2)建立目标函数:

f(Xj)=‖P1-Q1‖+‖P2-Q2‖+

‖P3-Q3‖+‖P4-Q4‖

(10)

其中,Pi为在相应测量模式下,根据式(3)得到不同旋转轴位置对应的球杆仪长度变化,Pi=[pi,1pi,2…pi,n]T;i=1,2,3,4分别对应A轴球杆仪径向、A轴球杆仪轴向、C轴球杆仪径向、C轴球杆仪轴向4种测量模式;Qi为测量模式i下采集的不同旋转轴位置的球杆仪长度变化,Qi=[qi,1qi,2…qi,n]T。根据式(10)计算个体Xj的适应值f(Xj),并将f(Xj)中最小值对应的个体设为当前最优个体Xbest。

(3)变异操作产生个体:

(11)

(4)交叉操作产生个体:

(12)

其中,m为1～D内的随机整数;cr为(0,1)内的随机数;CR为交叉算子,其一般取值范围为 0.3～0.9[15]。

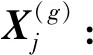
(13)

(6)选择最优个体。根据下式选择当前迭代的最优个体:

(14)

(7)判断是否达到最大迭代次数,若达到最大迭代次数,则算法结束,输出最优解,否则转到步骤(3)。

1.3 PIGEs辨识仿真

设机床A轴的运动范围为30°～-90°,C轴的运动范围是0～360°。设定各项误差如表1所示,各项误差设定值分为Ⅰ、Ⅱ组,其中,Ⅰ组误差较小,Ⅱ组误差较大。球杆仪公称长度L=100 mm、球杆仪工作台端的接触球球心与C轴回转轴线在X方向的距离RB=32 mm,与A轴轴线在Z方向的距离ZT=164 mm,如图4所示。差分演化算法中设定的参数如表2所示。

表1 PIGEs辨识结果(仿真)

表2 差分演化算法参数表(仿真)

图4 参数RB、ZT示意图

将设定参数代入式(3),获得4种测量模式的球杆仪长度变化曲线;使用TSUTSUMI等[11]提出的辨识方法获得PIGEs初始解;使用差分演化算法辨识PIGEs,获得更准确的PIGEs。仿真计算中,差分演化算法所使用的参数如表2所示,机床旋转轴PIGEs辨识结果如表1所示。

由表1可看出,旋转轴PIGEs较小时,使用TSUTSUMI等[11]提出的辨识方法获得的PIGEs接近设定值。PIGEs较大时,本文方法比TSUTSUMI等[11]提出方法辨识的PIGEs更接近设定值,对应的球杆仪长度变化轨迹更接近目标轨迹(如图5所示),即基于差分演化算法的PIGEs辨识方法能够获得准确度更高的PIGEs。

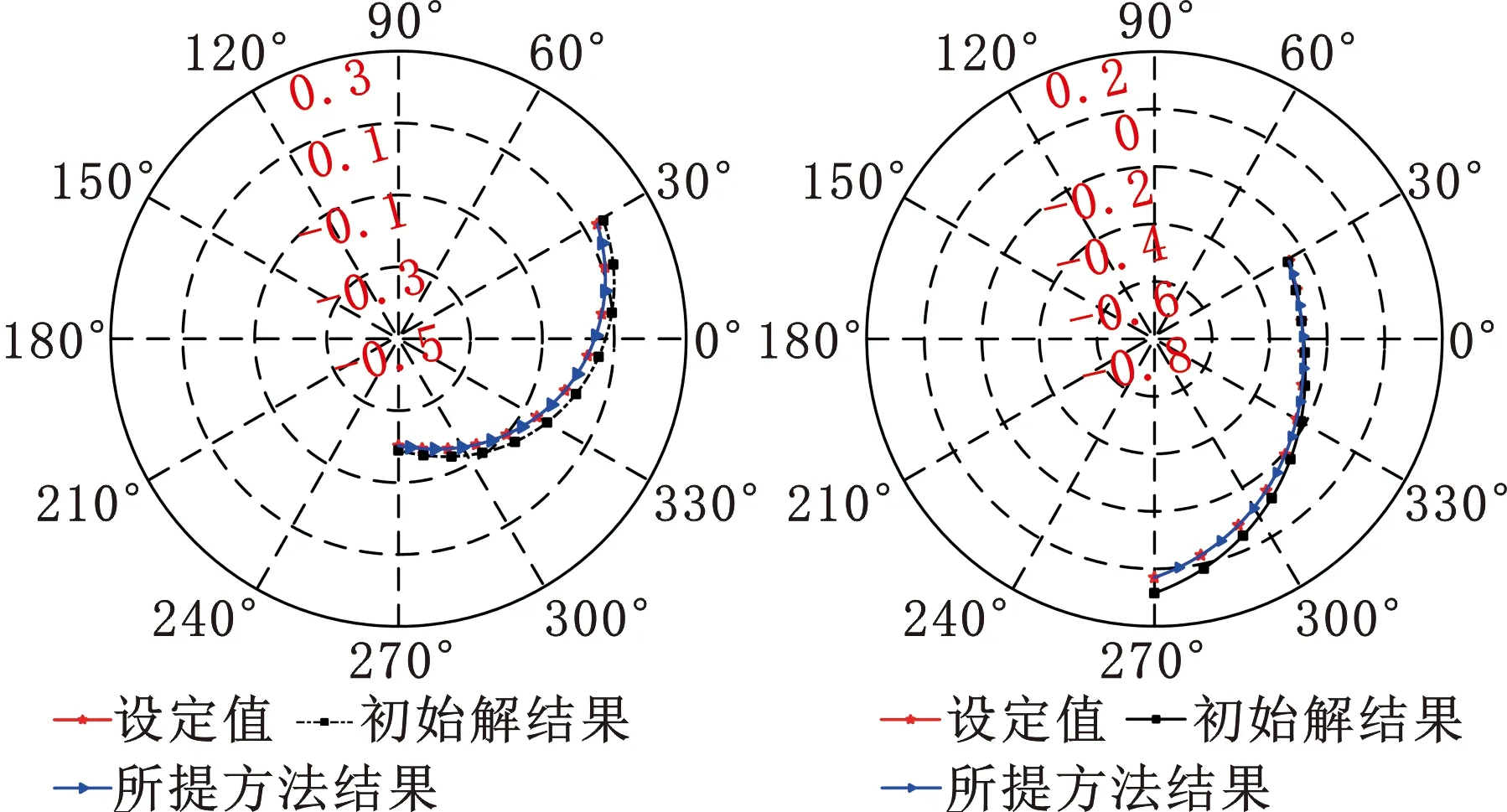
(a)A轴的球杆仪径向模式 (b)A轴的球杆仪轴向模式

2 PIGEs辨识实验

2.1 球杆仪安装

以A轴的球杆仪轴向测量模式为例说明球杆仪的安装步骤。首先,将带有磁性的工具杯安装在合适的刀柄上,再将刀柄安装在机床主轴上。然后,把球杆仪中心座安装在C轴台面,调整球杆仪中心座位置,使其与C轴轴线重合,再将中心球放置在球杆仪中心座上。然后使工具杯随机床主轴移动到球杆仪中心座正上方,移动Z轴使工具杯与中心座上中心球大致对齐,再微调X轴、Y轴位置,使工具杯对齐中心球。再缓慢移动主轴,使工具杯随着主轴沿Z轴方向缓慢下降,直到中心球在磁力作用下自动吸附在工具杯中,然后停止移动主轴并将该位置设为工件坐标系原点,锁紧中心座,使中心座固定在C轴台面。然后,将将主轴沿着Z向上升,再取下中心球。最后,使主轴往X轴正方向移动100 mm,再将主轴沿Z轴下降至z=0处,然后在中心座与工具杯之间放置球杆仪,此时球杆仪杆长方向与X向相同。A、C轴的球杆仪轴向、径向测量模式的安装如图6所示。

(a)A轴径向 (b)A轴轴向 (c)C轴径向 (d)C轴轴向

2.2 PIGEs辨识实验

本辨识实验中,L=100 mm,RB=32.1 mm,ZT=164.69 mm。机床进给速度设为1 m/min,球杆仪采样频率为1000 Hz。根据球杆仪的4种测量方式编写数控机床G代码程序,机床按照设定的轨迹运动,球杆仪采集长度变化量。根据TSUTSUMI等[11]提出的辨识方法获得PIGEs初始解(表3),将该初始解代入式(3)得到对应的球杆仪长度变化曲线。在初始解基础上,通过差分演化算法获得准确度更高的PIGEs(差分演化算法中设定的参数如表4所示),其辨识结果如表3所示,再将辨识结果代入式(3)得到对应的球杆仪长度变化曲线,上述变化曲线如图7所示。

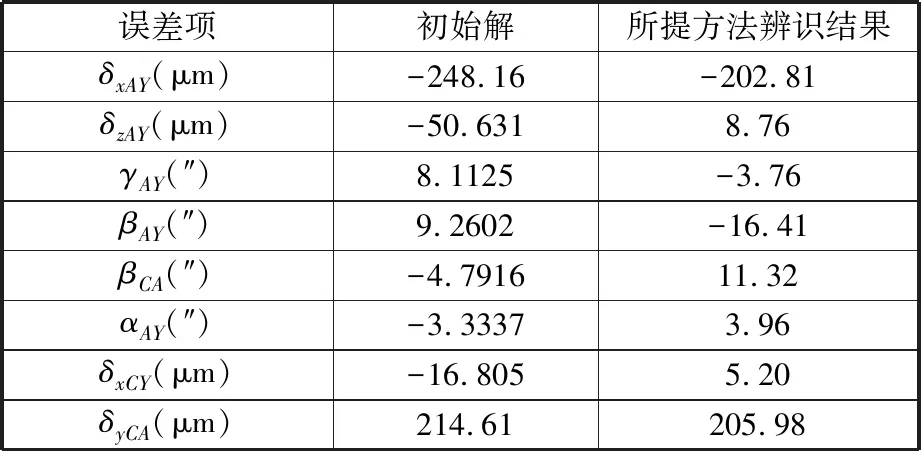
表3 PIGEs辨识结果(实验)

表4 差分演化算法参数表(实验)

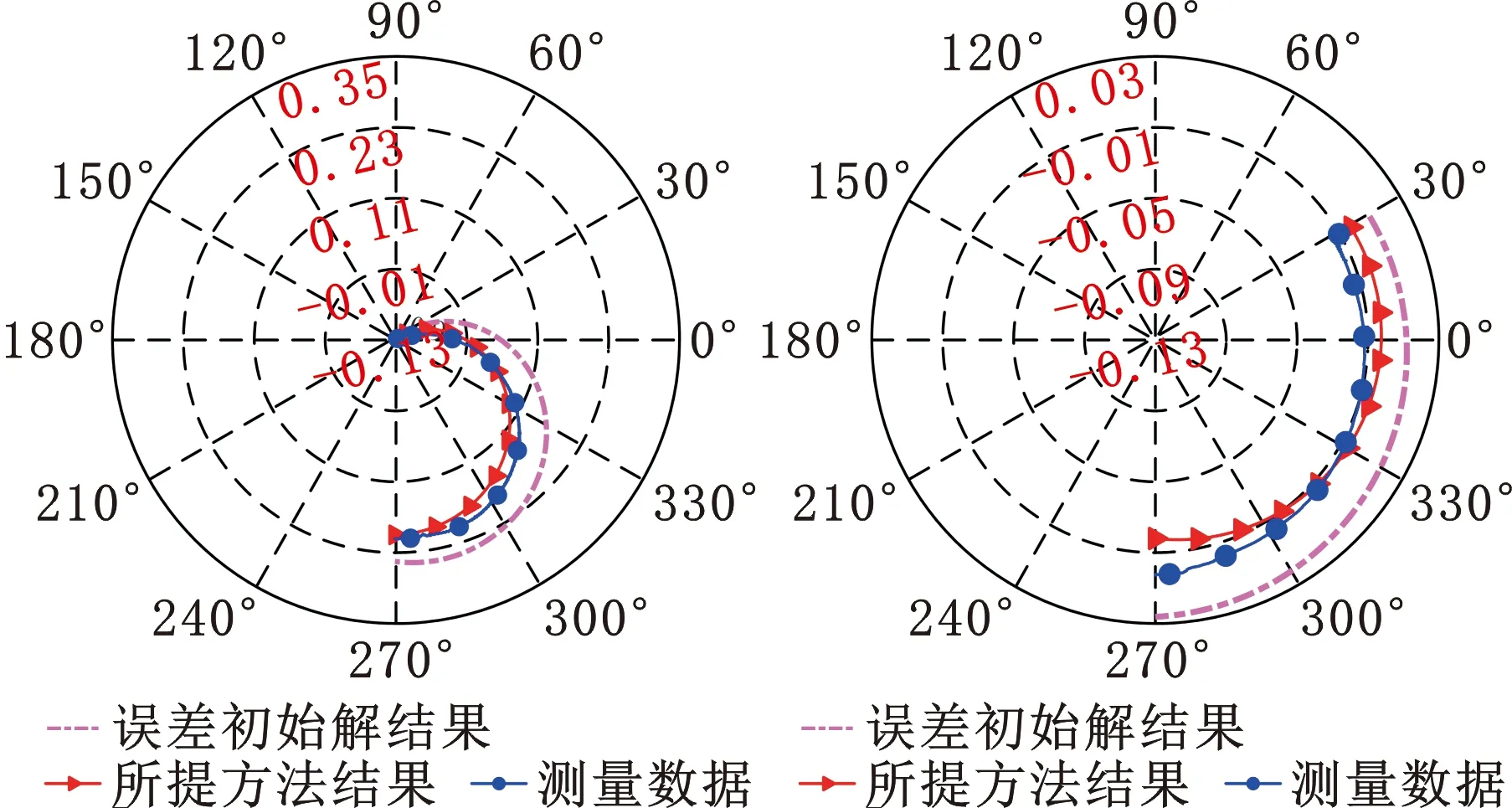
(a)A轴的球杆仪径向模式 (b)A轴的球杆仪轴向模式

由图7可看出,C轴的球杆仪径向测量模式下,3条轨迹差别不明显;其他3种测量模式下,相对于TSUTSUMI等[11]提出的辨识方法,本文方法的球杆仪长度变化曲线更接近球杆仪实测数据曲线,即基于差分演化算法的辨识方法可获得准确度更高的PIGEs。

3 结论

本文提出一种基于差分演化算法且无需简化机床旋转轴几何误差模型的旋转轴PIGEs辨识方法。首先基于经典的球杆仪轴向、径向测量模式辨识旋转轴的PIGEs,获得PIGEs初始解,然后利用差分演化算法整体优化求解旋转轴PIGEs,获得准确度更高的PIGEs。AC双转台型五轴机床实验验证了所提PIGEs辨识方法的有效性。