可形变自驱动粒子在不对称周期管中的定向输运*

郭瑞雪 艾保全

(华南师范大学物理学院,广州 510006)

粒子的随机运动被整流为定向运动是非平衡统计物理的重要研究内容.尽管如此,在活性粒子整流的研究中,粒子通常被视为刚性的.然而,在软物质中,粒子通常具有可变形的性质.本文重点探讨了可形变自驱动粒子在非对称周期通道中的定向运输行为.由于这些粒子具有可变形的特性,它们可以通过比自身小的通道.本文通过数值计算发现,可形变自驱动粒子能够打破热力学平衡,在空间不对称的条件下产生定向运动.粒子的集体运动方向完全由通道的不对称性决定.本文还发现,增加自驱动速度和粒子软化都能促进粒子的整流,而增大密度和旋转扩散则会阻碍粒子的定向运动.本文的研究成果有助于理解可形变粒子在受限结构中的定向运动行为,并为相关软物质马达的实验研究提供理论支持.

1 引言

作为生物学和物理学的前沿课题之一,分子马达的定向运动一直备受关注.这些微小的分子马达在生物体内能够将ATP 水解能转化为机械能,从而产生定向运动[1-3].它们在细胞内的物质定向输运方面发挥着关键作用,并几乎参与了生物体所有的生命活动,包括肌肉收缩、细胞运动和基因复制[4,5].因此,深入研究分子马达的运动特性具有重要意义.为了更深入地了解分子马达的运动特性,国内外学者从理论和实验两个方面进行了全面的研究.其中,布朗马达作为重要的理论模型为进一步探究分子马达的运动特性提供了理论支持[6-8].

布朗马达是一种利用时间或空间的不对称性将随机运动转化为定向输运的非平衡系统.该输运机制在物理学、生物学、纳米技术等领域引起了广泛关注和深入研究[9-13].根据非平衡驱动的差异,布朗马达模型可分为摇摆棘轮[14-17]、闪烁棘轮[18-21]和关联棘轮[22-24]3 种主要类型.摇摆棘轮中无偏向的外力引起系统的瞬态时间不对称,进而在周期不对称势中发生定向运动.闪烁棘轮模型中粒子在空间不对称的势场随机在两态或多态间跃迁或者采取势的时间调制来形成定向运动.关联棘轮模型主要考虑色噪声对整流的影响.其他类型的布朗马达模型则可视作上述3 种类型的扩展或组合,比如驱动蛋白的头部弹性连接,而势在两态之间闪烁的模型可归为闪烁的棘轮模型[25].研究各类布朗棘轮模型有助于深入理解定向输运行为,并为优化定向输运提供可能性[26].

在布朗马达系统中,以往对于不对称通道中的整流运动的研究已经覆盖了多种类型的粒子,包括活性粒子[27-29]、极性粒子[30]和手性粒子[31]等.这些研究中粒子都被看作是刚性的.然而,在细胞单层、发育中的组织、压缩泡沫和乳剂等软物质系统中,粒子往往是可形变的.而且,软/可形变粒子的形变特性会强烈影响系统的动力学行为[32-36].例如,可形变粒子可以通过明显小于粒子尺寸的通道并进行定向输运[37].因此,在受限结构中可形变粒子如何影响定向运动是一个有趣但尚未解决的问题.

为了解决这一问题,本文研究了在二维不对称周期管中可形变的自驱动粒子,并重点考虑了可形变特性对粒子的定向输运的影响.对于可形变自驱动粒子,自驱动会破坏热力学平衡,在空间不对称条件下产生定向输运.粒子的集体运动方向完全由周期管的不对称性决定.增大粒子的自驱动速度和粒子软化都会促进粒子的整流,而增大密度和旋转扩散则会阻碍粒子的整流.此外,在大的自驱动速度下,粒子的可形变特性对定向输运的影响更加显著.

2 模型和方法

考虑N个可形变自驱动粒子在二维周期不对称管中的运动.二维不对称周期通道的形状可以用其半宽度来描述(如图1(a)所示):

图1 (a)可形变粒子在二维不对称周期通道中运动的示意图,通道的形状利用其半宽度来描述((1) 式),x 方向施加周期边界条件,y 方向 施加反射边界条 件;(b)由20 个顶点 构成 的多边形粒子,{xm,c,ym,c}表示多 边形m 的质心,{xm,i,ym,i} 表示 多边形 m的第 i 顶点的位置Fig.1.(a) Scheme of deformable particles moving in a two-dimensional asymmetric periodic channel,the shape of the channel is described by the half width of the channel(Eq.(1)),periodic boundary condition is imposed in the x -direction and reflection boundary condition in the y -direction;(b) the deformable polygonal particles with 20 vertices,{xm,i,ym,i} is the position of vertexi in the polygon m and {xm,c,ym,c} is the center of mass of the polygon m.

其中LL1+L2为通道的周期.通道的最小宽度和最大宽度分别为W和2H+W.定义一个不对称参数Δ(L1-L2)/L来描述通道的不对称性,当Δ0 时通道是完全对称的.在通道的x方向施加周期性边界条件,在y方向则施加反射边界条件.类似的几何结构被广泛地应用于非平衡定向输运的研究中[38,39].

其中,第1 项是收缩项,它将顶点之间的连接视为弹簧常数为kl、平衡长度为l0的弹簧.第2 项是粒子面积am的二次项,描述其不可压缩性,其中ka和a0分别表示面积刚度模量和目标面积.第3 项是弯曲项,其中kb表示弯曲刚度.无量纲的形状参数A(Nvl0)2/(4πa0) 控制粒子的形变能力,A越大则表示粒子越软.对于具有Nv个顶点的规则多边形有AvNvtan(π/Nv)/π,且当Nv→∞时,Av1,这意味着顶点可以形成平滑的几何图形.在几何学中,标准圆对应于A/Av1,正五边形对应于A/Av1.16,正六边形对应于A/Av1.1.

可形变粒子的质心的自驱动速度大小为v0,方向为nm(cosθm,sinθm),其中θm满足如下方程:

其中,Dθ为旋转扩散系数.通常情况下,热扩散可以用高斯白噪声来描述,因此,这里的ξm(t) 表示具有单位方差和零均值的高斯白噪声,满足统计关系:〈ξm(t)〉0,〈ξm(t)ξm(t′)〉δ(t-t′).

构成多边形的顶点i的运动可以用过阻尼朗之万方程描述:

为了计算粒子之间的排斥相互作用,将每个顶点都视为直径δl0的圆盘(如图1(b)所示).通过将接触的多边形上的重叠粒子间的排斥相互作用相加,从而得到了总的排斥相互作用能为[34]

式中,kr是排斥相互作用的强度,Θ是Heaviside阶跃函数.

由于可形变粒子沿y方向的运动受到通道边界的限制,因此只关注沿x方向的集体运动.在足够长的时间下,粒子沿x方向的平均速度可以表示为

模拟中采用随机欧拉算法对方程(3)和方程(4)进行数值积分,积分时间步长 dt0.001,总积分时间t105,以确保系统达到非平衡稳态.无特殊说明时,将设置参数为µ1,N100,Nv20,klka1,kb0,kc10,L20,W4,H4,以及Dθ0.01.

3 结果与讨论

3.1 通道不对称性对定向运动的影响

图2 描述了不同自驱动速度v0的情况下,粒子的平均速度Vs随不对称参数Δ的变化关系.研究结果表明,自驱动速度能够使系统远离平衡,从而发生定向输运,且定向运动方向完全由通道的不对称性决定的.当Δ ＜0时,粒子的平均速度为正,Δ ＞0时,粒子的平均速度为负,Δ0时,定向输运消失.这种现象可以解释为,粒子倾向于向斜坡平缓的一侧移动.当Δ ＜0时,通道的最大宽度的左侧更陡,因此,粒子更容易向更平稳的右侧移动,即〈Vs〉＞0.同理,当Δ ＞0时,〈Vs〉＜0.当Δ0时,通道是完全对称的,粒子在两个方向上运动的概率相同,因此 〈Vs〉0.因此,定向运动的方向完全由通道的不对称性决定,N,A,v0等参数仅影响平均速度的大小,而不影响运动方向.因此,在下文讨论中,只考虑Δ ＜0 的情况,设置Δ-0.8,并通过改变密度φ、形状参数A、自驱动速度v0和旋转扩散系数Dθ来研究可形变粒子的定向输运.

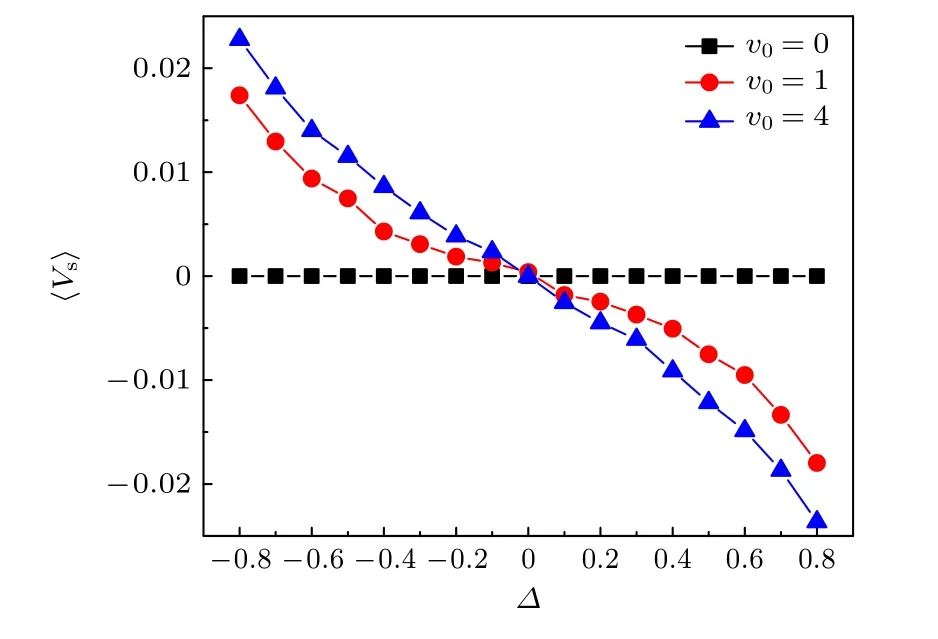
图2 平均速度〈Vs〉随不对称参数 Δ 在不同 v0 下的变化曲线,A1.16Fig.2.Average velocity 〈Vs〉versus the asymmetric parameter Δ for different v0 at A1.16.

3.2 自驱动速度对定向运动的影响

图3 为不同φ值下,平均速度 〈Vs〉随自驱动速度v0的变化曲线.其中,可以观察到较大的v0会促进可形变粒子的整流.当v0→0时,系统处于平衡状态,〈Vs〉→0.当v0不断增大时,非平衡驱动增强,持续长度Lpv0/Dθ ≫L,使粒子容易通过熵垒,便于粒子通过不对称管道.另外,发现随着速度的增大,粒子的拉伸效应会变得更加显著,拉伸效应也会进一步促进粒子的整流.然而,当φ较大时,随着v0的增大,粒子与瓶颈快速接触会加剧拥堵,从而会阻碍棘轮输运;但是当v0足够大时,粒子有足够的动能跨越瓶颈.因此当φ较大时,〈Vs〉-v0曲线中会出现凹值的现象.

图3 平均速度 〈Vs〉随自驱动速度 v0在不同φ下 的变化曲线,A1.16Fig.3.Average velocity 〈Vs〉versus the self-propulsion speed v0 for different φ at A1.16.

3.3 旋转扩散对定向运动的影响

图4 为不同v0时的平均速度 〈Vs〉随旋转扩散系数Dθ的变化曲线,从图中可发现平均速度〈Vs〉随Dθ的增大而逐渐减小.这是因为持续长度Lp(Lpv0/Dθ)在逐渐减小,导致粒子通过通道更加困难.当Dθ →∞时,持续长度Lp→0,活性粒子变为被动粒子,系统中没有非平衡驱动,因此定向输运消失.

图4 平均速度 〈Vs〉随旋转扩散系数 Dθ在不同v0下 的变化曲线,A1.16, φ0.625Fig.4.Average velocity 〈Vs〉versus the rotational diffusion coefficient Dθ for different v0 at A1.16 and φ0.625.

3.4 粒子软化对定向运动的影响

形状参数A越大,粒子越容易变形和变软.图5(a)为不同v0下,平均速度 〈Vs〉随形状参数A的变化关系.从图5(a)可以观察到在较小的v0下,形状参数对平均速度的影响很小,而在较大的v0下,〈Vs〉随形状参数的增大逐渐增大.随着A的增大,粒子被软化,这意味着粒子的面积可以增大,甚至大于初始面积.粒子的面积越大,拉伸效应就越明显.因此在v0较大时,形状参数A的增大会促进粒子的整流.而v0较小时,粒子的拉伸效应不是很明显,此时A对整流的影响较小.图5(b)描述了〈Vs〉在v0-A平面的相图,从图中能够更清晰地观察〈Vs〉随v0和A的变化情况.当固定A时,平均速度〈Vs〉随着速度增大而变大.固定较小v0时,A对平均速度的影响非常小,当固定较大v0时,A对平均速度的影响较大.

图5 (a) 平均速度〈Vs〉随形状参数A 在不同v0下的变化曲线;(b) 平均速度 〈Vs〉在v0-A 平面的相图,φ0.625Fig.5.(a) Average velocity 〈Vs〉versus the shape parameter A for different v0 at ϕ0.625 ;(b) phase diagram of the average velocity 〈Vs〉in the v0-A representation at φ0.625.

3.5 粒子密度对定向运动的影响

图6 为不同v0下的平均速度〈Vs〉随着密度φ的变化曲线.从图6 可以观察到密度的增大会阻碍粒子的定向运动,而且这个影响在大v0时比在小v0时更为显著.因为对于小v0的情况,粒子有足够的时间变形及调整使其顺利通过瓶颈.而对于大v0的情况,粒子会迅速接近瓶颈,粒子数的增加会加剧粒子的堵塞,使其通过通道的难度增大,从而阻碍了棘轮输运.

图6 平均速度 Vs随密度φ在不同v0下的变化曲线,A1.16Fig.6.Average velocity Vs versus the density φ for different v0 at A1.16.

3.6 多粒子和单粒子的对比

最后,在φ相同的情况下,将多粒子和单粒子运动情况进行比较.在这种情况下,设置单粒子的面积等于多粒子面积之和.图7(a)—(c)分别描述了多粒子和单粒子的平均速度 〈Vs〉随A,v0,Dθ三个参数的变化关系.结果表明,虽然多粒子和单粒子都可通过通道瓶颈,但多粒子更能促进整流.事实上,尽管单个可形变粒子能够通过比其自身尺寸更小的通道瓶颈,但当它分裂成多个可形变粒子时,显然更容易通过通道瓶颈,从而促进粒子的整流.

图7 φ0.625时,单粒子和多粒子的平均速度〈Vs〉分别随 A, v0, Dθ 的变化曲线Fig.7.The average velocity of single particle and many particles 〈Vs〉is taken as a function of A, v0,and Dθ at φ0.625.

4 结论

本文通过数值模拟研究了二维不对称周期通道中的可形变自驱动粒子的定向输运.粒子的自驱动速度作为非平衡驱动,打破热力学平衡,在空间不对称的条件下产生定向运动.研究结果表明,粒子的定向运动方向完全由通道的不对称参数决定,粒子更倾向于向较平缓的一侧运动.粒子自驱动速度的增大和粒子的软化能够促进棘轮输运.特别是在大自驱动速度下,粒子的拉伸效应会更加明显,粒子软化对定向输运的促进会更加显著.然而,密度和旋转扩散的增大会阻碍粒子的整流.密度的增大会导致粒子堵塞,使其通过通道变得更加困难.而旋转扩散的增加则会导致粒子运动的持续长度减小,同样使得粒子通过通道更加困难.当密度一定时,相较于单个可形变粒子,多个可形变粒子总是促进整流的.

细胞的集体运动在组织生长、伤口愈合和免疫反应中起着重要的作用,这对于理解病理机制,如癌症和转移的形成也很重要.在本文中,粒子的形状可以用多自由度来描述,这比以往用于描述软/可形变粒子系统的模型更有优势.从结果来看,可形变粒子可以通过明显小于自身尺寸的通道瓶颈,并进行定向输运,这不同于以往刚性粒子的结果.本文的研究结果有助于理解可形变粒子在受限结构中的输运行为,并为相关的软物质实验提供理论支持.期望这些结果能够促使细胞集体运动的进一步实验研究,以深入了解与集体细胞运动相关的生物过程.