基于量子计算的高能核物理研究*
2023-11-16李天胤邢宏喜4张旦波
李天胤 邢宏喜4)† 张旦波
1)(华南师范大学量子物质研究院,原子亚原子结构与量子调控教育部重点实验室,广州 510006)
2)(华南师范大学量子物质研究院,广东省核物质科学与技术重点实验室,广州 510006)
3)(华南师范大学南方核科学计算中心,粤港量子物质联合实验室,广州 510006)
4)(华南师范大学物理学院,原子亚原子结构与量子调控教育部重点实验室,广东省高等学校物质结构与相互作用基础研究卓越中心,广州 510006)
高能核物理旨在探索和理解物质在夸克与胶子层次的组成及演化的基本规律.然而,从量子色动力学第一性原理出发来求解高能核物理,经典计算却存在本质困难.近几年来,量子计算因给模拟高能核物理提供了潜在的根本性解决方案而受到了较大的关注.本文简要回顾了高能核物理量子模拟的现状,介绍了态制备及光锥关联函数测量等典型量子算法,并通过强子散射振幅和有限温有限密物质相结构的研究,分别展示了量子计算在解决高能核物理中含时问题和符号问题上的优势.
1 引言
高能核物理研究夸克与胶子及其强相互作用形成的物质及其演化,对理解物质深层次结构乃至宇宙起源均具有重要意义.高能核物理的底层模型量子色动力学(QCD)具有色禁闭的关键特征,即在低能标时QCD 处于强耦合区域,夸克和胶子等被束缚在色中性的强子中,不能单独存在.由于夸克禁闭的存在,高能核物理中的许多重要物理量,如强子散射振幅,具有非微扰特性,导致由第一性原理的QCD 理论出发来理解高能核物理存在基本困难.另一方面,理解核物质在不同温度及密度下的物态特性,即核物质相图,是高能核物理的另一个重大挑战.这是由于在有限密度情形,格点QCD 的蒙特卡罗模拟存在符号问题,从而无法保证精度.总而言之,经典计算机在模拟高能核物理中的含时演化问题[1]及有限密度核物质上[2],均存在本质困难.
高能核物理经典模拟存在困难的本质在于它属于强关联量子多体系统.一个根本性的解决方案是通过可控量子系统来模拟QCD 及相关的高能核物理,此即量子计算模拟方案.量子计算机最先由费曼在1982 年提出[3],Jordan,Lee 和Preskill(JLP)[4]最早在2012 年证明了量子计算机以多项式复杂度模拟标量场中的散射问题.近年来,随着量子计算机硬件及量子算法的快速发展,量子计算与高能核物理的交叉研究逐渐成为研究热点,其中包括核子结构中部分子分布函数的计算[5-10]、部分子簇射问题[11,12]、与环境有相互作用的开放系统动力学问题[13-15]、非平衡态热力学问题[16,17]、高能核物理中散射振幅的计算[18,19]等含时问题[20,21].另一方面,量子计算也用于模拟高能核物理中有限温有限密系统,如有限温有限密系统的手征相变的量子模拟[22-24]、手征磁效应的量子模拟[25]、以及如何在量子计算机上通过变分量子算法来模拟高温时夸克的禁闭-退禁闭行为[26].
本文主要对我们近期基于量子计算模拟高能核物理的工作进行综述[9,10,19,26].第2 节介绍了在高能核物理中常用的量子算法;第3 节介绍了如何基于第2 节所提的量子算法计算强子散射振幅;第4 节则介绍如何通过量子计算机来研究有限温有限密核物质;最后第5 节是对这一系列工作的总结.
2 高能核物理相关量子算法
在量子计算机上模拟高能核物理一般包含两部分:制备描述强子或核物质的量子态,以及在该态上进行物理量的测量.本节基于量子线路模型的数字量子计算机,介绍相关的典型量子算法.
2.1 强子态制备
如何在量子计算机上模拟一个强子?最核心的步骤是制备描述强子的量子态.强子态是给定量子数下的激发态.从多体波函数的角度出发,强子态一般极为复杂,包含夸克及胶子各种构型的叠加,具有较复杂的量子关联.对于NISQ(noisy intermediate-scale quantum era)量子计算机,变分量子本征值求解器[27-30]是制备强子态的适用方法,通过采用合适的波函数拟设,可以满足量子数的要求并精确表达强子态.该算法的框架如图1所示.首先,采用量子数保持的拟设,即试探波函数由保持系统对称性的参数化幺正算符U(θ)作用到给定量子数的参考态|ψlk〉ref上,

图1 变分法制备强子态的量子线路图.其中量子计算机通过拟设U(θ)来生成试探波函数以及测量试探波函数下El(θ)的值.经典计算机负责更新和优化参数θFig.1.Variational quantum algorithm for preparation of the hadronic state.The generation of trial state and the measurement of El(θ) are performed on a quantum computer,while the optimization of parameters θ is done with classical computing.
其中l代表系统除能量外的所有量子数,k代表给定量子数l下的第k个激发态.参考态|ψlk〉ref为类Dicke态,其一般的制备方法可在文献[31]中找到.
保持系统对称性的幺正算符U(θ)可以通过交替算符演化拟设[32,33]来构造.为此,先把哈密顿量分成n(≥2)份,HH1+···+Hn,并满足以下要求:1)每一个Hi都与哈密顿量H具有一样的对称性;2) [Hi,Hi+1]0 对所有i成立;3)选取尽量大的n.U(θ)可以通过多层n个哈密顿量H1,···,Hn的交替演化来构造:
其中p是演化的层数.
制备强子态的第二步是最优化目标函数El(θ)[28],
其中wli满足wl1>wl2>···>wlk >0.在最优参数θ*得到之后,量子数为l的第k激发态强子可通过|h〉U(θ*)|ψlk〉ref来制备.值得强调的是,El(θ)通过量子-经典混合计算的方式来优化(如图1 所示),其中量子计算机制备试探态并进行测量,经典计算机收集测量数据并更新参数θ,迭代直至收敛.
2.2 有限温度系统的平衡态制备
在QCD 相图中,核物质在不同温度、不同密度下呈现不同的物态,特别地,在温度非常高时,夸克出现解禁闭现象,与胶子构成了夸克-胶子等离子体,一直以来是高能核物理的研究重点.然而,传统的格点色动力学计算方法在模拟有限密度核物质时存在符号问题.在量子计算上,可以直接制备有限温度系统的平衡态[34-38],亦即热态或吉布斯态,该方法不基于概率来采样,对零密度及有限密度均适用,从而避免了符号难题.与强子态制备类似,变分量子算法适用于在NISQ 量子计算机上模拟有限温系统[36,39,40].然而,制备热态需最小化自由能,过程中熵的测量对量子计算机而言是较大的挑战[36,39].下面介绍一种变分量子算法,通过特定的拟设避免了熵的测量,同时对一般系统的热态又有很好的表达力.
该算法的关键在于试探态可由参数化的幺正算符U(ϕ) 作用到初始混态生成
其中ρ0(θ)为直积态,ω(θ,ϕ).由于U(ϕ) 是幺正的,它不会改变熵.又由于初态具备的直积形式,系统的熵S(ω) 可表达为单比特混态ρi(θi)上的熵之和.由此,系统的变分自由能可写为
其中β1/T.在参数空间中最优化自由能,即可得到最优参数ω*,则吉布斯态为ρ(ω*).与强子态制备的变分量子算法类似,自由能的优化通过量子-经典混合计算的方式进行,如图2 所示.

图2 可同时制备吉布斯态和计算自由能的变分算法量子线路图.在量子计算机中执行的是初始混态的制备和参数化幺正演化 U(ϕ),而参数(θ,ϕ) 的优化通过经典计算机来执行Fig.2.A pictorial representation of the variational quantum algorithm,which can prepare thermal states and compute the corresponding free energy.The preparation of initial mixed state and the evolution U(ϕ) are done on a quantum computer,while the optimization of(θ,ϕ) should be done with a classical computer.
2.3 关联函数的测量
在态制备之后,量子模拟的另一个重要环节是对态进行测量,得到描述该系统的物理量.物理量一般通过关联函数来揭示,它包含静态关联函数及动力学关联函数.在量子计算机上,静态关联函数只需对量子比特进行关联测量即可.动力学关联函数的测量更为复杂,具体算法可参考文献[41].在核子结构的研究中,部分子分布函数、碎裂函数等非微扰量的计算依赖于一种特殊的两点动态关联函数,即光锥关联函数,涉及了光锥上两个算符的关联.此外,散射振幅也需要通过计算含时的多点关联函数得到.动力学关联函数涉及了哈密顿量演化,属于典型的含时演化问题.相对经典计算机,量子计算机在求解动力学关联函数上具备天然的优势.
先考虑一般形式的两点关联函数

图3 计算动力学两点关联函数量子线路.在辅助比特上测量 σ1和σ2 即可得到关联函数的实部和虚部Fig.3.Quantum circuit for calculation of the two point correlation function.The real and imaginary part of the correla tion function can be obtained by performing measurements of σ1 and σ2 on the auxiliary qubit,respectively.
上述即为计算两点动力学关联函数的量子算法,对于多点动力学关联函数,只需令辅助量子比特分别控制多点关联函数对应的算符并在相邻的两算符间插入对应的时间演化算符即可.值得注意的是,哈密顿量演化 e-iHt需通过Trotter 分解的方法表示为量子门的组合[42],从而适用于在数字量子计算机上运行.
3 强子散射振幅的量子计算
在高能核物理中,散射截面是联系理论和实验的桥梁,散射振幅是计算散射截面不可或缺的一部分,因此具备重要的地位.强子散射过程是指初态有强子参与或者末态有强子产生的散射过程.根据末态探测粒子数目的不同,可对强子散射过程进行分类.1)e+p →e′+X,在末态只测量一个电子的信息而忽略其他X粒子,该类过程被称为单举过程;e+p →e′+h+X,在末态测量电子和一个强子h的信息,该类过程被称为半单举散射过程;e+γ →e′+h,把末态粒子信息全部测量完的被称为遍举过程.在QCD 因子化定理适用范围下,初态有强子参与的单举过程可被因子化成微扰可计算的硬部分卷积非微扰的部分子分布函数(parton distribution functions,PDFs[43,44]);末态只生成一个强子的遍举过程散射振幅则可被因子化为硬部分卷积的非微扰量,即光锥分布振幅(light cone distribution amplitudes,LCDAs[45,46]).从物理含义上看,PDFs 反映了强子内部部分子的纵向动量分布,介子LCDAs 则描述了一对正反夸克在遍举过程中如何强子化成介子.PDFs 与LCDAs 均为计算强子散射振幅必要的输入.格点QCD 发展了许多方法来尝试计算PDFs[47-62]和LCDAs[63-66].然而,由于PDFs 和LCDAs 均为含时演化问题,依赖于光锥关联函数的求解,对格点QCD 而言存在经典计算的本质困难.此外,在碰撞能量较低时,QCD 散射过程可看作是强子间的弹性散射.由于QCD 耦合常数在低能标时较大,微扰论失效,散射振幅可通过格点QCD 间接求解[67-71],但缺乏一般性的直接求解方法.
总的来说,运用格点QCD 的方法解决上述关于强子散射振幅的非微扰问题存在困难.本节将介绍如何基于量子计算的方法来求解高能散射紧密关联的三个问题,包括单举过程对应的PDFs、遍举过程对应的LCDAs,以及低能情形且初末态强子数目较少过程的散射振幅.
3.1 Nambu-Jona-Lasinio 模型
由于近期的量子计算机计算能力有限,规范场的模拟仍较难在量子计算机上实现.为了从数值上验证量子算法的有效性,我们选取1+1 维Nambu-Jona-Lasinio(NJL)模型[72-74]作为例子.NJL 模型是一个四费米子自相互作用模型,可视为QCD的低能有效理论,且具有手征对称性自发破缺与渐近自由等和QCD 一样的特点.其拉格朗日量为
其中Ψ是费米子场,m和g为别为裸夸克质量以及NJL 模型耦合常数.
在量子计算机上模拟NJL 模型的第一步是对其进行离散化.采用交错费米子,离散化之后的费米子场可由单分量场χn表示.通过Jordan-Wigner[75]变换,可将费米子场映射成量子比特形式:
该变换可保持费米子场的反对易关系.在该离散化机制下,两个量子比特对应着一个空间格点,近期约100 量子比特的量子计算机可模拟约50 个空间格点.NJL 模型的量子模拟对量子比特数资源需求较小,有利于在近期量子计算机上开展研究.在周期边界条件下,NJL 模型的哈密顿量可写成HH1+H2+H3+H4,其中
3.2 部分子分布函数的量子计算
PDFs 是计算强子初态单举过程散射截面的重要输入量.PDFs 一般被记为fi/h(x,µ),其物理意义是在能标μ下,非极化部分子i占据非极化强子h的纵向动量份额为x的概率密度.夸克PDFs算符定义为
Pexp 表示路径顺序指数,τa是盖尔曼矩阵,是SU(3)规范场.从算符定义可以看出,PDFs 的量子计算包含了3 个关键步骤:1)制备强子态|h(P)〉;2)构造威尔逊链W(0) ;3)在量子态|h(P)〉上测量动力学两点关联函数.
由于NJL 模型没有规范场,我们用NJL 模型来具体讨论如何通过步骤1)和步骤3)来实现PDFs 的计算,而对步骤2)的部分仅做一般性的讨论.在强子参考系下,光锥关联函数D(z)可写为
其中|h〉表示的是零动量强子态|h(p0)〉.PDFs可通过D(z)的傅里叶变换得到
其中mh为强子的静质量,x表示部分子的动量份额.
D(z)的量子计算如图4 所示,包含强子态制备和光锥关联函数的测量,分别对应图中虚线的左右部分的量子线路.具体来说,NJL 模型的强子态|h〉是能量最低的一对正反夸克束缚态,它是与真空具有一样量子数的第一激发态.由此,制备|h〉态需要两个参考态:

图4 部分子分布计算的量子线路.其中虚线左边部分为制备强子态的量子线路,右边部分为测量动力学两点关联函数线路Fig.4.Quantum circuit for calculation of PDFs.The left side of the dashed line of the circuit is for hadronic state preparation,while the right side is for the correlation function.
在给定参考态后,试探波函数由(2)式中U(θ)作用到参考态上生成,为此,只要将U(θ)中的Hi具体化为NJL 模型哈密顿量(10)且选取pN/2.在最优化目标函数(3)后即可制备出真空态|Ω〉U(θ*)|ψΩ,1〉ref和强子态|h〉U(θ*)|ψΩ,2〉ref.成功制备强子态之后,只需把强子态作为图4 虚线右侧量子线路的输入即可计算出D(z).
图4 所示量子线路的复杂度为O(N3)[33,42].量子算法复杂度随着量子比特数以多项式标度增长说明了在量子计算机上计算PDFs 具有优势.更进一步的分析表明,量子优势在更高维度,如3+1 维且含规范场的情况下仍能保持[9].
下面展示1+1 维NJL 模型夸克PDFs 的结果.我们使用Quspin[76]以及ProjectQ[77]在经典计算机模拟图4 中的量子线路.为了控制有限体积效应和有限格距效应的影响,要求无量纲的强子质量满足条件 2π/N <mha <π.同时,考虑到量子计算经典模拟的指数复杂度,选取格点数9(对应量子比特数N18)和无量纲质量ma0.8.图5 分别给出了D(z)的实部和虚部在g0.6 和g1.0情况下的结果.从图5 可以看出,D(z)的实部与虚部相比基本为零,这意味着fq(x) 满足奇函数条件fq(x)-fq(-x).PDFs 在减掉真空图后一定会有fq¯(x)-fq(-x)[78],结合fq(x) 是奇函数,可得到fq(x)fq¯(x),这与NJL 模型中强子态|h〉由一对正反夸克组成相自洽.

图5 坐标空间夸克场两点关联函数的实部(实线)和虚部(虚线),其中离散的点是格点计算给出的数值,线由格点数据结果插值得到Fig.5.Real(dashed lines) and imaginary parts(solid lines)of the quark correlation function in position space.The discrete points are the lattice data and the lines are obtained by interpolations.
部分子分布函数的结果在图6 中给出.由于格点有限体积效应的存在,fq(x) 在非物理区域x >1有小的非零值,这一现象同样存在于格点QCD 的计算当中[79].可预期在增加格点数后,fq(x) 在区间x >1 处的非零值会进一步被压低.我们在结果中观察到了fq(x)在x0.5 处具有一个峰值,这一定性行为与二维格点QCD 的计算结果[80]以及JAM合作组从实验数据提取出的介子PDF[81]相符.

图6 量子计算经典模拟获得的PDF(空心点)和格点NJL模型精确对角化获得的PDF(实线),其中不同插值方法带来的误差由误差棒标记出Fig.6.The quark PDF from quantum computing(open markers) and ED(solid lines).The error bars/bands arise from the estimated uncertainties due to different interpolation methods.
3.3 基于量子计算方法对LCDAs 的研究
介子LCDAs 是计算遍举过程散射振幅的重要非微扰输入量,其物理意义可看作是一对分别携带强子纵向动量份额为x和1-x的正反夸克对结合成大动量强子的概率幅.介子LCDAs 的算符定义为
在强子参考系下,1+1 维单味道NJL 模型的介子LCDA 可写成
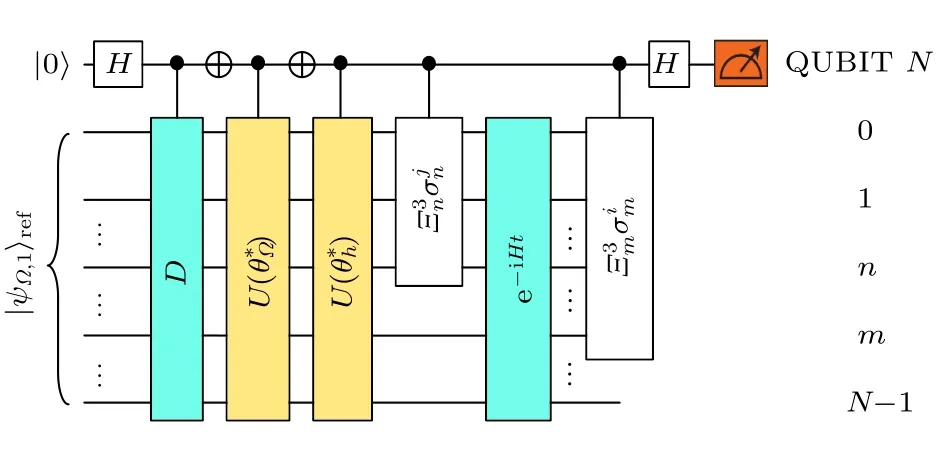
图7 模拟左矢为真空,右矢为强子的光锥关联函数〈Ω|O|h〉的量子线路图Fig.7.Quantum circuit for the light-cone correlator〈Ω|O|h〉.
以下展示数值模拟的结果.如图8 所示,实线(ED)代表的是对格点NJL 模型进行数值精确对角化的结果,空心点代表的是量子计算经典模拟的结果,二者的符合体现了量子算法的准确性.此外,LCDA在x1/2 处的峰随着g →0 变得越来越尖锐且趋近于LCDA 的渐近形式[45,46,82].此外,由于有限体积效应,LCDA在x >1 以及x <0 非物 理区间有振荡衰减的非零值.这一现象也存在于格点QCD 对LCDA 的计算当中[83].图9 还给出了LCDA 对强子质量mh的依赖关系.图中分别选择mh1.3a-1,1.5a-1,1.7a-1和固定g0.1,N14,可见随着强子质量的增大,LCDA在x1/2 处的峰变得越来越尖锐,这一定性行为与格点QCD 的结果相符[83].

图8 1+1 维NJL 模型LCDA 对耦合常数g 的依赖,其中固定 N 14,mh 1.5a-1Fig.8.LCDA for the 1+1 dimensional NJL model with N 14,mh 1.5a-1.

图9 1+1 维NJL模型LCDA 对强子质量mh 的依赖,其中固定 N 14,g 0.1Fig.9.Dependence of the LCDA on the hadron mass mh with fixed bare coupling g 0.1 in the 1+1 dimensional NJL model.
3.4 LSZ 约化公式及散射振幅的量子计算
Jordan,Lee 和Preskill(JLP)[4,84,85]的系列论文证明了量子计算机可通过多项式复杂度计算标量场高能过程散射截面.然而,JLP 方案需要制备初态波包,对计算资源要求较高.另外,JLP 方案里未涉及束缚态粒子,而QCD 的散射过程的初态往往会有强子态出现,因此难以直接使用.为此,基 于Lehmann-Symanzik-Zimmermann(LSZ)约化公式[86],我们提出量子计算束缚态粒子的散射振幅的一种新途径.LSZ 公式把散射过程的散射振幅和真空多点关联函数联系在一起.对于质量为m,可被标量场ϕ湮灭的粒子h参与的散射过程h(k1)+···+→h(p1)+···+,其散射截面可表达成
其中NNin+Nout.G({pi},{kj}) 是动量空间的连通n点关联函数:
其中T表示的是时序,下标“con”表示关联函数的连通部分,|Ω〉是真空态.K(p) 是动量空间的两点关联函数,
其中R是场强归一化常数,它的定义为
其中|h〉表示零动量的单个h粒子态,它可以是强子态.依据(19)式,散射振幅的计算被分为3 个部分:1)计算连通N点关联函数G({pi},{kj}) ;2)计算传播子K(p) ;3)计算场归一化常数R.1)、2)两个步骤都是在计算多点关联函数,他们可统一通过2.3 节提到的量子算法来计算.步骤3)中R的计算类似于LCDAs,只不过算符替换成ϕ(0),因此R可用LCDAs 的量子算法来计算.
下面来讨论这一量子算法的复杂度,假设待模拟的格点QFT 系统共有M个空间格点以及M个时间格点,表达一个空间格点上的场自由度需要nq个量子比特,那么在该系统计算N点关联函数的复杂度为,它指数依赖于N.因此,该算法适用于初末态粒子数量较少的散射过程,如2→2散射过程.
作为一个例子,我们依然以1+1 维NJL 模型这一简单模型为例来具体给出量子算法的运行结果,并通过这些结果来演示量子算法的合理性.在下面的模拟中选取量子比特数N14,无量纲裸夸克质量为ma0.84,耦合常数为g0.4.
在动量趋于h的质壳附近时,1+1 维单味道NJL 模型两点函数KΨ有如下发散行为:
依据(23)式可知,当固定p10时,KΨ(p) 作为p0的函数在p0±mh处会有奇点结构.为验证这一奇点结构,可通过量子计算的经典模拟来实现3.2 节所提量子算法,先计算坐标空间两点关联函数,再通过傅里叶变换得到KΨ(p).图10 展示了以p0为自变量的两点关联函数 TrKΨ(p) 的实部.图中在p0a±1.18 附近处的峰对应着夸克质量峰.峰位置的准确性已经由精确对角化格点NJL 模型所给出的强子质量谱所验证.在连续极限下,这个峰的高度将变为无限大,对应着奇点结构;对于有限格距情况下,这个峰只能有有限的高度.

图10 1+1维NJL 模型 TrKΨ(p) 的实部.图中以 p0 为变量,固定p1 0Fig.10.Real part of TrKΨ(p) for the 1+1-dimensional NJL model as a function of p0a with p1 0.

NJL 模型的这一简单例子表明量子算法成功实现了传播子和n点连通关联函数所期望的奇点结构,这对LSZ 约化公式在量子计算机上的实现至关重要.
4 有限温格点施温格模型的量子模拟
核物质相图的确定是高能核物理研究中的一大挑战,它依赖于对有限温度有限密度QCD 系统平衡态的精确模拟,而格点QCD 方法在有限密度情形存在符号问题的困难.量子计算机在模拟有限温有限密度平衡态系统上具有天然的优势,目前已经用于物态结构的探索[22-26].由于近期量子计算机资源的限制,目前有限温有限密度QCD 的量子模拟还有待发展.本节将通过另一个较简单的模型来阐述有限温核物质的模拟,特别是在高温情形时的夸克解禁闭行为.该模型为施温格模型,它描述了1+1 维量子电动力学,包含了费米子与U(1)规范场的耦合.与QCD 类似,施温格模型存在夸克禁闭[87,88]、手征对称性自发破缺[89,90]等特征.因此,施温格模型被广泛用于模拟高能核物理问题.
在选定规范A00 情况下,施温格模型的哈密顿量可表达为[91]
其中Ψ(x) 是费米子场,是电磁矢势的纵向分量,m是裸费米子质量.
由于局域规范不变性,电场和电荷密度算符之间存在约束∂1E(x)gΨ(x)†Ψ(x),即满足高斯定理.在1+1 维时,电场可以通过费米子来表示.这是施温格模型的一个重要特点,即可表示为长程相互作用的费米子模型,规范场不出现,从而非常方便用量子比特来模拟.采用交错费米子[92],并通过Jordan-Wigner 变换[75],施温格模型可写为
其中ε是背景电场,ϖ1/2a.更进一步,若要研究有限密度势情形,则需在(25)式加一个额外的项 -[93],其中μ为化学势.
在零温时,施温格模型中正反夸克间具有与长程QCD 相似的线性势[94],此即夸克禁闭.可看作夸克之间由一根弦连接,弦张力可衡量禁闭强度[95],它会随着热涨落的增强而减小.弦张力定义为系统自由能在零和非零背景电场下的差别[96]:
其中β1/T是温度的倒数,Fε(β) 是对应哈密顿量Hε的自由能.从弦张力的定义可知,计算弦张力只需计算自由能的差.计算自由能的量子算法已在2.2 节中给出.我们用开源程序包 QuTip[97]来进行量子计算的经典模拟.为了验证量子算法的正确性,在结果中把量子模拟的结果与精确对角化的结果进行比对.首先模拟了施温格模型弦张力对温度的依赖关系,如图12(a)所示,弦张力在小β区间会迅速衰减,这表明弦张力会因热涨落效应变强而减小.特别地,弦张力在β0,即温度无限高时趋于零,表明施温格模型的禁闭-退禁闭转变发生在无穷温度.图12(b)表明弦张力的大小随着温度的增加指数下降,且ε越小下降得越快.弦张力的指数衰减行为与理论预言相一致[96].
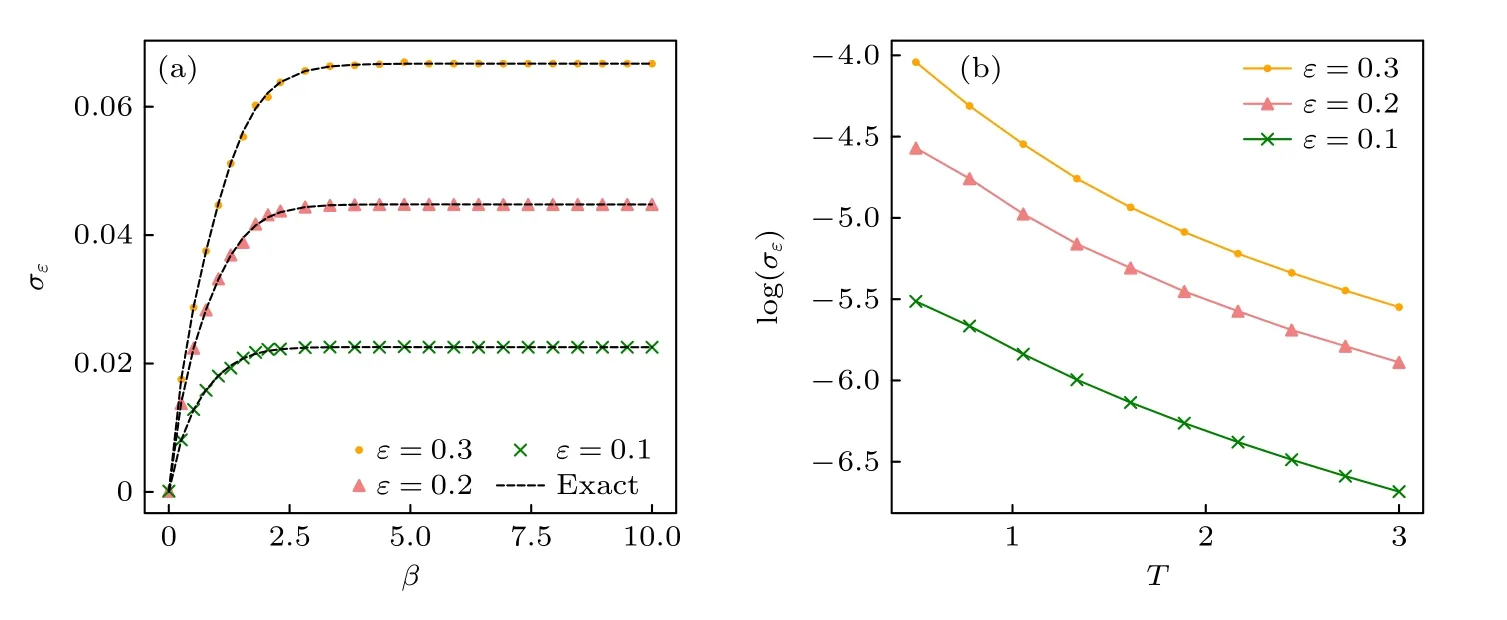
图12 不同背景电场 ε 下的弦张力.其中给定 m1, g 1, ϖ 1,N=6(a) 弦张力对 β 的依赖;(b) 弦张力的对数对温度 T 的依赖Fig.12.String tensions under different ε in the case m1, g 1, ϖ 1,N=6:(a) The string tension as a function of the inverse temperature β ;(b) logarithm of the string tension as a function of the temperature T.
进一步对有限温有限密度情形下的弦张力进行了计算.图13(a)给出的是弦张力对不同化学势的依赖关系,可发现在相同温度下,化学势越大对应的弦张力越小.图13(b)给出了弦张力对温度和化学势两个变量的依赖关系.图中可见随着温度和化学势的升高弦张力都会减小,这与QCD 相图的行为类似[98-101].然而,与QCD 不同的是,施温格模型弦张力只有在T →∞时才会下降到零,这表明在有限温情形下施温格模型相图不存在禁闭-退禁闭相变.尽管如此,施温格模型相图仍能从定性上看出禁闭-退禁闭相变的一些性质,并且成功展示出量子计算模拟有限密度区域相结构的可行性.

图13 在给定参数 ε0.5, m1, g 1, ϖ 1, N 6 下的弦张力(a) 不同化学势 μ 下弦张力对温度 T 的依赖;(b) 弦张力对温度 T 和化学势μ 的依赖Fig.13.The string tension in the case ε0.5, m1, g 1, ϖ 1,N 6 :(a) At different μ,the string tension as a function of the temperature T ;(b) the string tension as a function of the temperature T and the chemical potential μ.
5 总结
本文对我们近期基于量子计算机来模拟高能核物理的系列工作进行了综述.针对强子散射问题,系统提出了以多项式复杂度计算PDFs和LCDAs 的量子算法,其中包括量子数分辨的变分量子本征求解器以及光锥关联函数的测量两大部分,并通过NJL 模型的数值模拟,初步展示了量子计算在定性上已经能给出合理的结果.此外,基于LSZ 约化公式,提出了强子散射振幅的量子计算新方案,避免了初态波包制备的困难,并适用于束缚态粒子的散射问题.还对有限温有限密度核物质的量子模拟进行了探索.通过施温格模型,展示了量子计算机可以模拟夸克在高温情形出现的禁闭-解禁闭行为.本文的研究初步展示了量子计算在解决高能核物理中含时问题和符号问题的可行性及优势,有助于进一步探索物质深层次结构及核物质相图.本文提出的强子态制备及结构探测是普适的量子算法框架,有望在高能核物理领域中广泛运用,如模拟部分子碎裂函数(parton fragmentation functions,FFs),模拟核效应的产生机制等.同时,针对1+1 维施温格模型发展的有限温量子热态的量子算法,有望拓展到2+1和3+1 维下非阿贝尔规范场,从而模拟有限温有限密度情形的QCD 相图,有望揭示QCD 禁闭相到退禁闭相的转变.总而言之,量子计算为未来研究高能核物理中的含时非微扰问题以及有限温有限密相结构问题提供了一个潜在的根本性解决方案.
