财政补贴对企业全要素生产率的影响研究——基于新结构经济学理论

徐 锴

(贵州财经大学 大数据应用与经济学院, 贵阳 550025)

当前我国经济已由高速发展阶段向高质量发展阶段迈进,但受制于资源环境约束增加、生产要素成本上涨、国际竞争愈演愈烈等诸多因素,亟须寻找经济增长新动能。党的二十大报告强调“加快建设现代化经济体系,着力提高全要素生产率”,为实现长期可持续的经济增长提供了路径思路。在市场经济体系中,企业是最具活力的微观市场主体,企业层面生产效率的提升是推动整个社会要素生产率提升的基础。新结构经济学认为,充分竞争的市场机制是促使企业按照比较优势发展,进而推动技术创新及生产率效率改善的基础性制度安排。然而,由于发展中国家软硬件基础设施的缺失及企业创新发展中不可规避的公共性、外部性等问题,仅依靠市场机制不能全面实现资源有效配置。此时,政府可以伸出“有形之手”,引导、扶持、规范产业经济主体发展。财政补贴作为政府干预市场的重要手段,在弥补市场失灵、引导资金流向、促进可持续发展等方面发挥至关重要的调控作用。因此,本文基于“有为政府”与“有效市场”协同视角,实证研究政财政补贴与企业全要素生产率的关系。

1 文献综述

大部分学者认为,政府的财政补贴能够促进企业全要素生产率的提高,主要表现在两个方面:①融资约束是制约企业全要素生产率提升的重要因素[1],财政补贴能够直接缓解企业内源融资压力,增加内部资金流动性,降低企业生产经营的边际成本[2]。同时,补贴向外部投资者传递着企业积极向好发展的信号,企业所面临的外源融资约束也得以缓解[3],进一步提高经营效率和生产效率。②技术创新是实现全要素生产率提升的重要途径。财政补贴能够帮助企业分摊创新风险,降低研发成本[4]。同时,技术创新具有较强的外部性,财政补贴作为一种补偿机制,能够有效缓解市场失灵带来的创新扭曲现象。

也有学者指出,财政补贴会抑制企业全要素生产率的提升,主要分为两个角度:①补贴会加重企业对于补助资金的依赖而滋生企业惰性。一方面,高强度的财政补贴会加速企业僵尸化[5],不利于市场“优胜劣汰”机制运转,阻碍资源有效配置;另一方面,财政补贴可能会诱发企业寻租行为[6],挤出用于正常生产经营的要素资源。②补贴对象的选择可能存在一定的偏误。一方面,在政企间信息不对称的背景下,企业通过“伪装”自己来骗取补贴[7];另一方面,在晋升“GDP锦标赛”的激励下,地方政府在补贴政策制定时往往偏向于实现短期宏观经济目标(如保障就业、增加地方收入等)而非企业效率最大化[8]。

梳理已有文献可知,财政补贴对企业全要素生产率同时存在正向促进和反向抑制两种影响,因而补贴效果具有高度的不确定性。基于此,从理论和实践两个层面对财政补贴与企业全要素生产率之间可能存在的非线性关系展开研究,同时,考察企业面临的市场竞争强度对补贴效果的影响。

2 理论基础与研究假设

2.1 理论基础

新结构经济学认为,经济增长的前提是生产效率的提高。提高生产效率需要要素禀赋结构与产业结构相协调。具体而言,通过产业结构的变迁将劳动力、资本、土地等生产要素配置到效率更高的产业或通过技术创新来实现,在这个过程中要注重软硬基础设施的建设不断与生产力发展相适应。经济体在某一时点上最优的产业结构内生于这一时点上的要素禀赋结构,而在自然资源有限、劳动力增速稳定的情况下,要素禀赋结构的升级主要取决于资本积累的速度(包括人力资本和物质资本)。基于此,新结构经济学主张根据现有要素禀赋结构采取符合比较优势的发展战略,使得企业选择更优的生产结构,从而提升企业自生能力并改善生产效率,推动资本积累和经济增长,最终改变下一时点上的要素禀赋结构,形成一种良性循环机制。然而,在实际经济运行过程中,企业关注的不是要素禀赋和比较优势这样的抽象概念,而是如何降低成本,提高收益。为了使得微观经济主体选择的技术和产业与要素禀赋的结构特性相适应,需要市场和政府(软基础设施)的双重力量对经济系统的传导路径加以修正和完善,实现资源的优化配置。基于此,以新结构经济学为理论基础对财政补贴与企业全要素生产率的关系和市场竞争强度的调节作用展开分析。

2.2 研究假设

2.2.1 财政补贴与企业全要素生产率

技术创新是提高企业要素生产效率重要驱动力。新结构经济学认为,无论技术创新成功与否,都将为发展中国家的产业升级和多样化提供有益的信息。然而,信息属于公共产品,如果探索性创新的“试错成本”全部由先行者承担并且创新成果的溢出效应引发其他企业的“搭便车”行为,就会抑制先驱企业的创新积极性。积极有为的政府可以通过财政补贴对先驱企业进行补偿,帮助企业克服创新障碍。随着研发投入的增加和技术的不断革新,企业全要素生产率得以提升。另一方面,有为政府还能够基于增长甄别的范式,配合实施因势利导的补贴政策,将生产要素配置到更具发展前景和成功经验的产业中,对具有潜在比较优势的先驱企业进行引导和扶持,改善这类企业的经营、投融资决策,在保证企业自生能力的前提下提高组织效率和生产效率,加速资本积累,最终改善全社会层面的要素禀赋结构。下一阶段的产业结构随之变迁,优化要素产出效率和配置效率,从而形成一种良性循环。基于此,提出以下假设。

H1:财政补贴能够促进企业提升全要素生产率。

财政补贴的初衷在于扶持产业发展、推动经济高质量增长。然而,在补贴政策设计和实施的过程中可供政府决策使用的信息较为稀缺,难以形成完整的信息链条从而引发政企之间的信息不对称[9]。实际上,补贴能否发挥积极作用还依赖于政府能否从诸多项目中甄别出真正需要支持的项目。在短期利益最大化目标的驱使下,高强度的财政补贴可能会触发企业“寻扶持”行为,加剧潜在的逆向选择问题。部分企业利用信息优势释放积极发展的虚假信号以争夺补贴资源,甚至会忽视市场实际需求,通过购买设备、投资建厂等方式盲目扩张。此外,更多的补贴资源在诱发企业寻租动机的同时削弱了企业通过技术创新、组织结构优化来提高生产效益的积极性。在这些情况下,财政补贴无法精确作用于那些具有比较优势和发展潜力的企业,从而造成补贴资源的错配和生产效率的损失,扭曲了政策实施的有效性。据此提出以下假设。

H2:财政补贴与企业全要素生产率之间存在倒U形的非线性关系,即一般情况下财政补贴的增加能够促进企业全要素生产率,而当财政补贴达到较高程度后转而会抑制企业全要素生产率提升。

2.2.2 市场竞争强度的调节作用

新结构经济学认为,在充分的市场竞争中形成的反映要素相对稀缺性的价格体系能够引导企业按照要素禀赋的比较优势来选择技术和产业,获得低要素成本的优势,从而推动生产效率的提高。但发展中国家存在软硬件基础设施的缺失以及创新发展中不可规避的公共性、外部性等问题,仅仅依靠市场机制不能全面实现资源有效配置。因势利导的财政补贴政策不仅能够在一定程度上降低由于市场的“短暂失灵”引起的非效率局面,还能为锐意进取的企业按照比较优势升级生产结构和创新发展提供资金支持,推动这些企业通过战略变革、技术变革和效率变革来获得竞争优势,因此,市场竞争与财政补贴之间存在互补性。

另外,为了在残酷的市场竞争中生存,企业的竞争策略趋于多样化。生产性策略(如通过技术创新提高产品市场竞争力)与非生产性策略(如通过自我“包装”获取更多财政补贴) 都有可能被使用。在监管制度不健全的背景下,企业通过骗补、寻租等非生产性手段获取竞争优势成为重要的策略,而通过技术创新等方式获得竞争优势具有时效性和滞后性且伴随着较大风险,对那些不思进取的企业而言并非最佳选择。当财政补贴强度过高时,市场竞争的深化可能会加剧这些“惰性”企业采取非生产性策略的动机,虽然能够满足企业自身短期利益最大化的目标,但却损害了企业生产效率。据此提出以下假设。

H3:市场竞争与财政补贴之间存在互补关系,即市场竞争强度的提高能够加深财政补贴与企业全要素生产率之间的倒U形关系。

3 研究设计

3.1 样本选取

自2015年供给侧结构性改革的实施,改善了以往财税激励政策实施过程中存在的创新质量战略的缺位、粗放型的投入方向等问题,为财税政策引导企业高质量发展提供便利。因此,基于2016—2021年非金融业沪深A股上市企业非平衡面板数据,对样本做以下处理:①剔除样本区间范围内曾为ST、*ST或PT类的企业;②剔除样本区间内有退市行为的企业;③剔除主要连续变量有缺失的样本;④为避免极端异常值的影响,对主要连续变量做上下1%的缩尾处理。

3.2 变量定义

3.2.1 被解释变量

全要素生产率。现有文献大多采用Olley和Pakes提出的计算方法(简称OP法)和Levinsohn和Pertin提出的计算方法(简称LP法)计算全要素生产率(total factor productivity,TFP)。其中,LP法使用中间投入品作为代理变量,通过替换变量的方式能够有效减少样本损失,相较于OP法更为精确。因此,本文采用LP法计算企业全要素生产率。

3.2.2 解释变量

财政补贴。参考柳光强[9]的研究,以企业年报中收到的“政府补助”并扣除所有的税收返还、即征即退、税收减免等财政补贴后,除以企业总资产来衡量企业接受的财政补贴强度。

3.2.3 调节变量

市场竞争强度。参考庄玉梅和王莉[10]的研究,用1减去勒纳指数衡量企业面临的市场竞争强度。此外,考虑不同行业间市场竞争具有异质性,对企业个体勒纳指数使用行业均值加以修正(将企业的营业利润率减去所在行业营业利润率均值),具体计算公式如下:

(1)

式中:OI为企业营业收入;OC为营业成本;i为企业个体;n为当年行业内的企业数。Lerner值越小,表明企业与同一行业其他企业有较大的业务相似性,面临的竞争就越激烈;反之,Lerner值越大,则面临的市场竞争强度越低。

3.2.4 控制变量

参考相关研究,选取:企业规模(Size)、企业年龄(Age)、盈利能力(ROE)、管理层薪酬(Salary)、股权集中度(Top10)、内部控制质量(Indir)为企业层面的控制变量。同时,在回归模型中加入了年度、行业、省份虚拟变量。所有变量的定义如表1所示。

3.3 模型构建

3.3.1 基准回归模型

为了验证财政补贴对企业全要素生产率的作用,在通过豪斯曼(Hausman)检验的基础上,构建如下固定效应模型:

TFPi,t=α0+α1Subi,t+α2Controlsi,t+Yeari+

Industryi+Provincei+εi,t

(2)

式中:TFP为以LP法计算得到的企业全要素生产率;Sub为财政补贴强度;Controls为控制变量集;i为企业个体;t为年份;Year、Industry、Province分别为年度、行业、省份固定效应;α0和ε分别为截距项和残差项。若回归结果中的α1显著为正,则可以说明财政补贴有效地提升了企业全要素生产率。

为了探究财政补贴与企业全要素生产率之间可能存在的倒U形关系,进一步将财政补贴的平方项引入式(2)的模型中,构建如下模型:

TFPi,t=α0+α1Subi,t+α2Sub_squi,t+α3Controlsi,t+

Yeari+Industryi+Provincei+εi,t

(3)

式中:Sub_squ为财政补贴的平方项。若回归结果中的α2显著为正(负),则说明财政补贴可能与企业全要素生产率之间呈现一种U形(倒U形)关系。

3.3.2 调节效应模型

为了验证市场竞争强度在财政补贴与企业全要素生产率之间发挥的调节作用,在式(2)和式(3)的基础上,构建如下调节效应模型进行检验:

TFPi,t=λ0+λ1Subi,t+λ2Lerneri,t+λ3Lerneri,t×

Subi,t+λ4Controlsi,t+Yeari+Industryi+

Provincei+εi,t

(4)

TFPi,t=η0+η1Subi,t+η2Subi,tsqu+η3Lerneri,t+

η4Lerneri,t×Subi,t+η5Lerneri,t×Subi,t_squ+

η6Controlsi,t+Yeari+Industryi+

Provincei+εi,t

(5)

式中:Lerner为市场竞争强度。式(3)主要用检验在仅考虑财政补贴与企业全要素生产率的线性关系时市场竞争强度的调节作用,若λ3显著为正(负),则说明市场竞争能够正向(负向)调节财政补贴对企业全要素生产率的激励效应。式(4)用于研究市场竞争强度对倒U形关系形状和拐点位置的调节作用。其中,若式(4)中η5显著为正(负),则市场竞争强度的提升显著舒缓(加深)了财政补贴与企业全要素生产率之间的倒U形关系。

4 实证分析

4.1 描述性统计

主要变量的描述性统计结果如表2所示。全要素生产率(TFP)的最大值为12.17,最小值为6.980,标准差为1.070,说明不同企业之间的全要素生产率之间存在较大差异,具有一定的研究价值。财政补贴(Sub)的最大值为2.690,最小值为0,标准差为0.5961,说明受企业性质和决策行为等因素的影响,不同企业享受到的财政补贴强度差异较大。同时,考虑到模型中可能存在的多重共线性问题,利用方差膨胀因子VIF进行检验,结果如表2最后一列所示。由表3可知,解释变量与控制变量的VIF均小于3,因此可以判定模型中不存在严重的多重共线性问题,故进行下一步的回归。

4.2 基准回归

表3中的第1列报告了未引入财政补贴的平方项并使用固定效应模型进行回归的结果。结果表明,变量财政补贴(Sub)的系数为0.025 8,并且在1%水平上显著,这说明在其他变量不变的情况下,企业享受的财政补贴每增加1%,企业全要素生产率会增加0.025 8%。因此,总体而言,财政补贴对于企业全要素生产率的提升起到了显著的正向激励作用,H1得到验证。

将财政补贴的平方项引入模型后,根据Lind和Mehlum[11]提出的U形曲线检验方法,逐步进行分析:第一,检验一次项系数和二次项系数的显著性。由表3第2列的检验结果可知,考虑控制变量的影响下,财政补贴(Sub)的系数均在1%的水平上显著为正,而财政补贴的平方项(Sub2)的系数在1%的水平上显著为负。第二,检验曲线的两个端点处斜率是否显著陡峭。根据第一步的回归结果,在考虑控制变量的情况下,对Sub求一阶导数后计算可得,当Sub取最小值时,斜率显著为正(slope=0.186 3),当Sub取最大值时,斜率显著为负(slope=-0.231 2)。第三,拐点的取值必须位于自变量的取值范围内。根据二次函数拐点测算公式可得,拐点取值为1.200 4,位于Sub的取值范围内。综上所述,以Sub为自变量而TFP为因变量的二次函数开口向下,两者呈现出一种倒U形关系。因此,当财政补贴低于一定水平时,对企业全要素生产率的提升存在促进作用,而过高的财政补贴可能会助长企业创新“惰性”,从而抑制全要素生产率产出的提升,H2得到验证。

4.3 稳健性检验

创新能力强、经营效率高的企业更容易受到政府补贴的青睐,因此,模型中可能存在由于反向因果而导致的内生性问题。基于此,选取同年度-同省份-同行业其他企业享受财政补贴的均值作为工具变量以缓解内生性问题。同省份同行业的其他企业享受财政补贴并不直接影响该企业的全要素生产率,从而确保该工具变量的外生性。同时,为验证该工具变量的有效性,对其进行“不可识别检验”和“弱工具变量检验”。其中,LM统计量为43.51(P=0.000),通过了不可识别检验;WaldF统计量大于Stock Yogo给出的weak ID临界值中10%偏误的临界值,表明该工具变量并非弱工具变量。在此基础上,采用二阶段最小二乘法(two stage least square,TSLS)再次进行回归估计。使用工具变量的回归结果如表3中第3列和第4列所示。可以看到,未引入财政补贴的平方项(Sub2)时,财政补贴对企业全要素生产率的影响在1%水平上显著,且符号为正;引入财政补贴的平方项后,一次项系数在1%的水平上显著为正,二次项系数在1%的水平上显著为负,且系数差异不大。说明在考虑内生性的情况下,财政补贴与企业全要素生产率之间的关系没有发生明显变化,原有的结论具备稳健性。

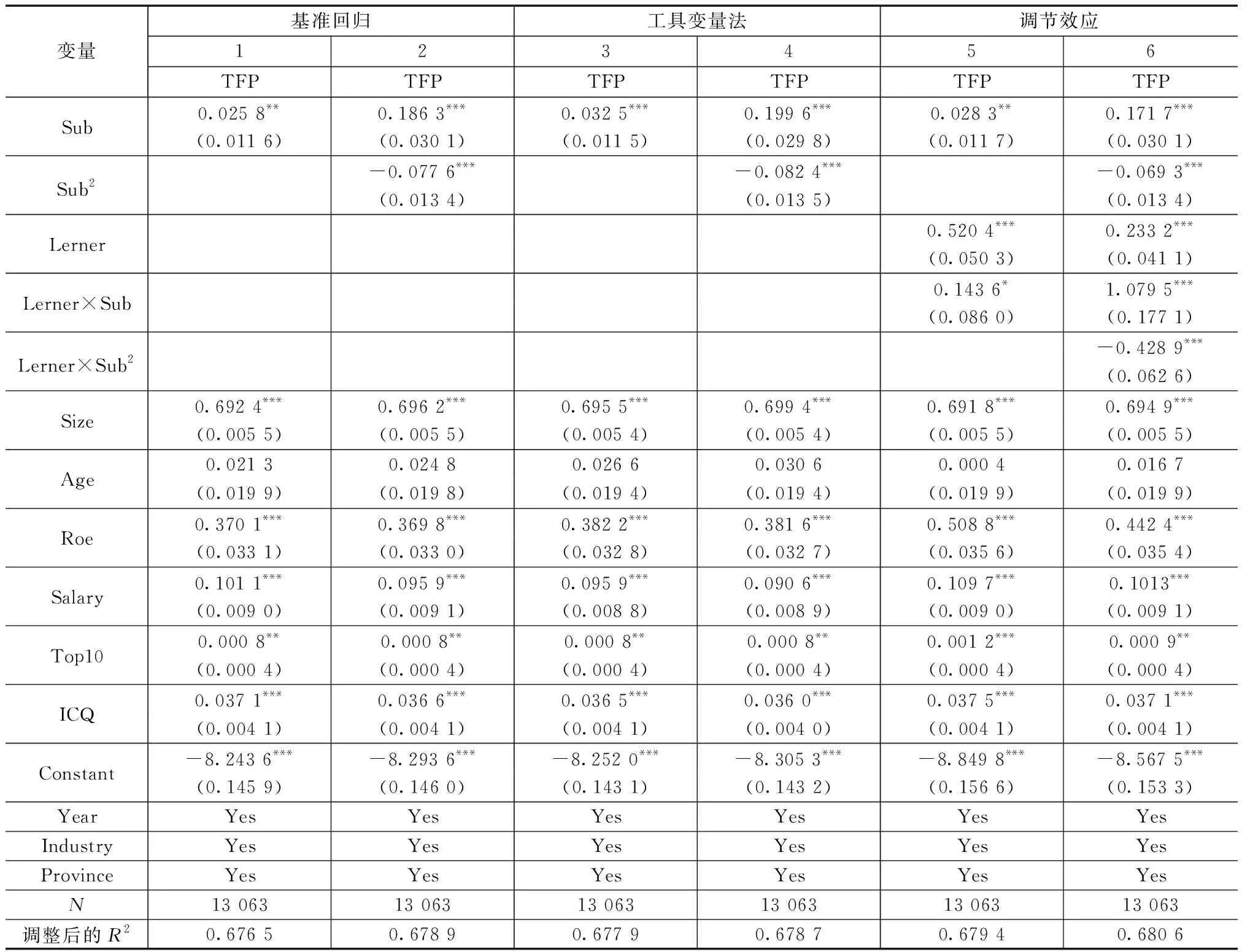
表3 检验结果

4.4 调节效应

为了考察市场竞争强度对财政补贴效果的调节作用,首先根据式(4)的模型进行检验。结果如表3中第5列所示。其中,市场竞争强度与财政补贴的乘积项(Lerner×Sub)系数为0.143 6,且在10%的水平上显著为正,说明在仅考虑财政补贴与企业全要素生产率之间存在的线性关系时,市场竞争强度起到了正向调节作用,即业内面临市场竞争强度越高的企业,财政补贴对企业全要素生产率的激励作用越强。前文在引入财政补贴的平方项(Sub2)后发现,补贴与企业全要素生产率之间存在倒U形关系,因此使用式(4)进一步分析调节效应,结果如表3第6列所示。其中,市场竞争强度与财政补贴的二次项的乘积项(Lerner×Sub2)的系数为-0.428 9,且在1%的水平上显著为正,说明市场竞争强度的提高,显著加深了财政补贴与企业全要素生产率之间的倒U形关系,H3得到验证。

此外,式(5)也可用于检验市场竞争强度的提升是否使得倒U形曲线拐点位置发生移动。步骤如下:求企业全要素生产率(TFP)对财政补贴(Sub)的一阶导数,该导数为0的点即为拐点

(6)

由式(6)可知,此时拐点位置取决于调节变量(Lerner)的值。因此,再根据式(6)对调节变量求导得

(7)

式(7)中分母恒定为正,因此当η1η5-η2η4>0时,倒U形曲线拐点随调节变量的提升向右偏移;当η1η5-η2η4<0时,拐点随调节变量的提升向左偏移。由表3中第6列的检验结果可知,η1η5-η2η4>0。因此,随着市场竞争强度的提高,倒U形曲线的拐点向右移动,拓宽了财政补贴适用区间的范围。

5 结论与启示

当今世界正经历百年未有之大变局,后疫情时代下中国经济发展在危机中育新机。在迈向科技强国的道路上,需要基于“有效市场”和“有为政府”的平衡作用机制,在两者协同进步中实现经济高质量发展。研究发现,适度的财政补贴能够激励企业提高全要素生产率,高强度的财政补贴反而会抑制企业全要素生产率的提升,两者之间呈现出一种倒U形关系;进一步研究发现,市场竞争强度的提高不仅能够加深财政补贴与企业全要素生产率之间的倒U形关系,还会推迟倒U形关系拐点的到来。鉴于上述结论,提出以下建议。

第一,建立财政补贴政策的绩效评价制度,并引入惩罚性激励政策,根据评价结果动态调整补贴方式和补贴对象,提高财政补贴的有效性。财政补贴宜适度,防止补贴资金过度集中于某些行业或企业,扩大补贴政策的惠及面。进一步完善政府各职能部门之间的沟通协调机制,推进政务公开,确保企业及时、准确地获取优惠政策信息,缓解政企间信息不对称问题。

第二,建立有效的反不正当竞争和反垄断的营商环境,营造统一开放、竞争有序的市场环境,保障企业合法权益,增强企业参与市场竞争的意识和能力。建立合理的行业准入规则,降低行业进入门槛与退出成本,破除地方保护和市场分割,保证所有企业依法平等地使用各种生产要素,实现资源的优化配置。增强地区间的经济凝聚力,形成科学合理的区域分工体系。