基于LightGBM和SVM的多属性砂体厚度预测

孙常凯,张云峰

(1.黑龙江省高校油气藏形成机理与资源评价重点实验室,黑龙江 大庆 163318; 2.东北石油大学 地球科学学院,黑龙江 大庆 163318)

地震属性是利用数学手段对地震资料的几何学、运动学、动力学及统计学等特征的一种表征形式,是地层信息和地质现象在地震资料中的反映[1]。不同岩性的地层在地震资料上的反映也不同,可以利用地震属性来预测地层的砂体厚度。然而,地震属性具有多解性,单一地震属性受到多种地质因素的共同影响,同时单一的地震属性难以全面地反映地层的特征,一个地质特征往往会在多个地震属性中都有体现[2]。因此,在预测砂体厚度时,需要将多种与砂体厚度有着较强相关性的地震属性结合起来。机器学习具有较好的解决非线性问题的能力,目前随机森林[3]、神经网络[4]和支持向量机[5]等机器学习方法均广泛应用于砂体厚度的预测中。

LightGBM(Light Gradient Boosting Machine)是一个实现梯度提升决策树(Gradient Boosting Decision Tree,GBDT) 算法的开源框架,由微软发布[6]。它具有更快的训练速度、更高的效率、更好的准确度以及更低的内存使用,并支持分布式、并行学习和GPU加速,以处理大规模数据。

支持向量机(Support Vector Machine,SVM)于1995年正式发表[7],在1996年被用于回归问题[8]。作为一种新的机器学习方法,已逐渐成为国内外研究热点之一[9]。该方法以统计学习理论和结构风险最小化为基础,利用核函数将有限维的低维空间映射到高维空间,以寻找合适的划分超平面来使样本可分,以解决低维空间的非线性问题[10]。该方法在解决小样本、非线性的问题上尤为合适,可以应对研究区样本少、断陷盆地砂体厚度变化复杂的问题[11]。

1 区域地质概况

陆东凹陷位于开鲁盆地陆家堡凹陷的东部,是发育于海西期褶皱基底上的中生代凹陷。凹陷受北北东向区域性断裂控制,构造走向由近东西向转北东向,具有南陡北缓、单断式断拗型的构造背景,即早白垩世以断陷为主,而晚白垩世则以拗陷为主[12]。

陆东凹陷构造演化可分为强烈断陷阶段(义县期)、快速沉降阶段(九佛堂期)、稳定沉降阶段(沙海期)、回返萎缩阶段(阜新期)。其中,九佛堂期的快速沉降阶段是由于陡坡带边界断裂强烈活动、盆地快速下降造成的。九佛堂早期沉降中心在后河地区,到九佛堂组晚期湖盆逐渐扩大。

盆地基地为古生界石炭、二叠系变质岩,其上依次覆盖中生界下白垩统义县组、九佛堂组、沙海组、阜新组[13],如图1所示。九佛堂组发育的半深湖—深湖相暗色泥岩沉积和近岸水下扇及扇三角洲沉积,形成了该区主要生、储岩系。

层位标定是储层预测研究的基础,也是属性分析的前提条件[14]。研究层位为九佛堂组,该层位由一个3级层序控制,可进一步划分为低位体系域、湖侵体系域和高位体系域[15]。其中,高位体系域主要为近岸水下扇—半身湖沉积体系,以泥岩、页岩为主,储层物性差,主要视为烃源岩和页岩油储层;对于低位体系域,由于钻遇义县组的井较少,导致可获得的低位体系域砂体厚度信息较少,难以进行模型训练。因此,湖侵体系域为研究的目的层段,该体系域主要为扇三角洲—滨浅湖沉积体系。前后河地区九佛堂组体系域如图2所示。

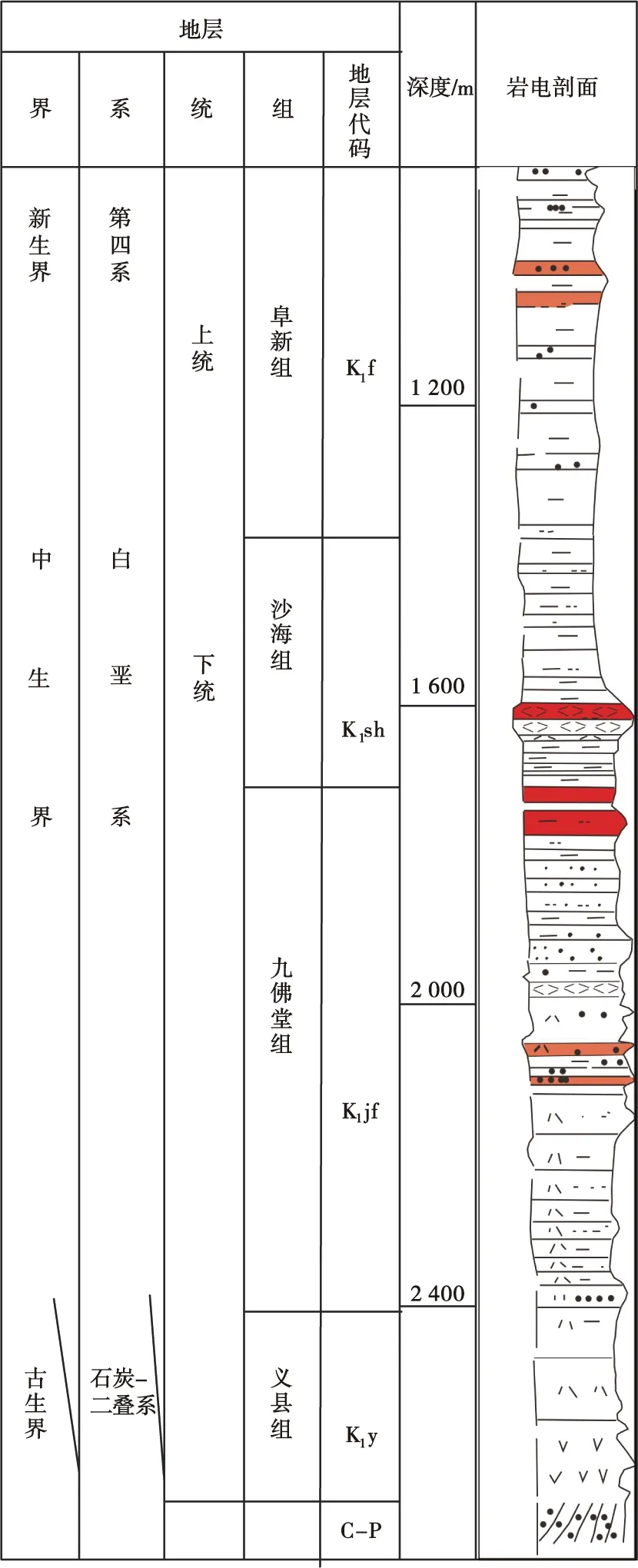
图1 陆东凹陷综合柱状Fig.1 Comprehensive histogram of Ludong sag

图2 前后河地区九佛堂组体系域Fig.2 Jiufotang Formation system tract in Qianhouhe area

整个陆东凹陷属于典型两洼夹一隆的构造格局,包括交力格、前后河和三十方地3个区块,前后河地区位于交力格洼陷和三十方地洼陷之间,如图3所示[16]。它包括前、后河断裂背斜及广发断裂背斜3个构造带,面积约170 km2,是陆东凹陷勘探的重要地区[17]。研究区东南部井网较密,而西北部井网较稀,难以仅用钻井资料描述砂体分布规律。因此,需要利用地震属性加以辅助。

2 研究方法

2.1 属性提取和建立样本集

研究利用Geoeast的GeoAttributeAnalysis子程序对研究层位进行地震属性提取,共提取99种地震属性,包括瞬时属性、时窗及振幅属性、子波属性、功率谱属性、自相关属性、单频属性、层序地层统计属性等。

砂岩厚度由井位录井资料确定,结合提取的地震属性,建立了样本集。研究区共35口钻穿湖侵体系域的井,因此样本数量为35。

2.2 特征选择

研究利用LightGBM来进行特征选择。LightGBM属于树模型,可以用来评估特征的重要性[18]。如果一个特征被选为分割点的次数越多,那么这个特征的重要性就越强。依据这个原理,可以进行特征选择。将所有地震属性作为特征进行模型训练,并留出30%的样本检验是否过拟合。训练得到的特征重要性见表1。其中,重要性为0的特征被省略。此时该模型的误差见表2。

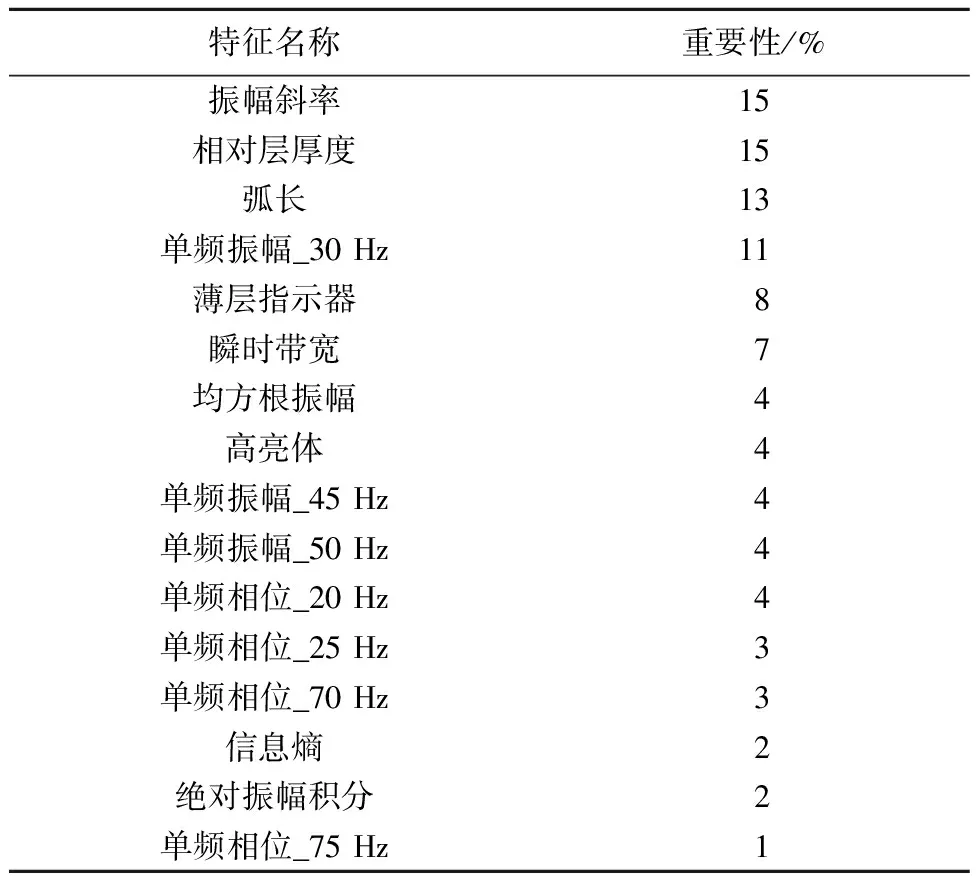
表1 初次特征选择的特征重要性Tab.1 Feature importance of initial feature selection

表2 初次特征选择的模型误差Tab.2 Model error of initial feature selection

其中,MSE为均方误差,RMSE为均方根误差,MAE为平均绝对误差,R2为决定系数。

可以看出,该模型发生了过拟合现象,将进一步进行特征选择。经过多次模型后,最终特征选择的结果见表3。

表3 最终特征选择的特征重要性Tab.3 Feature importance of final feature selection

此时该模型的误差见表4。

可以看出,此时模型的精度和泛化能力都较好。因此,选择这7种属性作为输入特征来进行模型训练,这7种属性如图4所示。然而,利用该模型得到的结果与实际地质情况不符,因而改用支持向量机进行预测,以发挥其在小样本问题上的优势。这7种属性分别为振幅斜率(Amplitude Slope,AmpSlp)、瞬时带宽(Instantaneous Bandwidth,IBand)、绝对振幅积分(Integrated Absolute Amplitude,IntAbsAmp)、相对层厚度(Thickness of Stratigraphic,ThkStrat)、单频振幅(Single Frequency Amplitude)、单频相位(Single Frequency Phase)、弧长(Arc Length)。

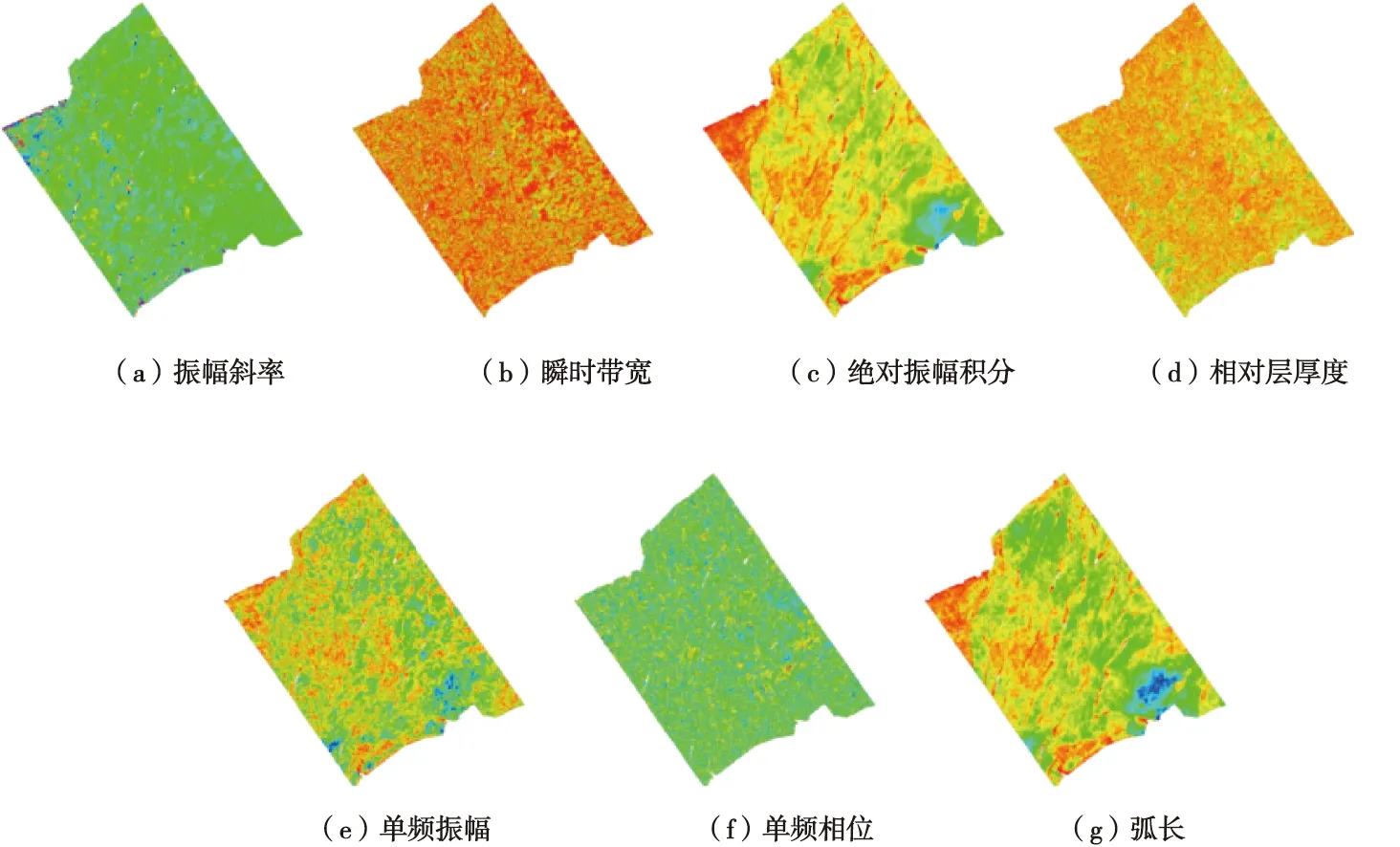
图4 地震属性图Fig.4 Diagram of seismic attributes

振幅斜率是时窗间隔内道记录振幅值随时间变化率的平均,可以表示储层中流体成分的变化、指示沉积环境以及识别断层[19];瞬时带宽是时窗数据内频率分布范围的统计量,地震波在油气等高衰减介质中传播时,会产生带宽的变化[20];绝对振幅积分是时窗间隔内所有振幅绝对值之和,可以预测地层的岩性[21];相对层厚度为光滑后的反射强度取相邻峰值之间的差值;单频振幅与单频相位是利用时频分析技术对地震信号进行分频解释,提高解释精度和可靠性,研究中选取的特征分别为30 Hz的单频振幅和20 Hz的单频相位;弧长是时窗内地震信号波形的弧长,它间接反映了地震信号的振幅与频率[22]。

2.3 标准化处理

LightGBM属于树模型,数值的缩放不影响分裂点的位置,因此无需对数据进行标准化处理。不同于LightGBM,支持向量机需要对特征进行标准化处理。不同的地震属性通常具有不同的量纲和数量级,而且不同地震属性之间的差距可能很大。为了消除地震属性之间的量纲和数量级对模型训练的影响,包括研究使用的支持向量机在内的多数机器学习算法,需要对原始数据进行标准化处理。研究使用z-score法进行标准化。z-score也叫标准分数,能够将不同量级的数据转化为统一量度的z-score分值,使其具有可比性。其公式如下:

(1)

式中,x*为变换后的值;x为某一地震属性的每个值;μ为该地震属性的均值;σ为该地震属性的标准差。

z-score变换后的地震数据符合正态分布,即均值为0,标准差为1[23]。

z-score标准化对数据分布有一定要求,正态分布的数据最有利于z-score标准化的计算,而非正态分布可能会导致z-score标准化的效果较差。绘制了7种属性的直方图来判断其是否服从正态分布,如图5所示。可以看出,除了瞬时带宽属性,其他属性虽然不是严格正态分布,但都有一定的正态性。因此,需要对瞬时带宽属性进行Yeo-Johnson变换[24],使其在一定程度上符合正态分布,改善其标准化效果。Yeo-Johnson变换公式如下所示:

(2)

式中,λ根据最大似然估计求得。

变换后的IBand属性的直方图如图5所示,可见其一定程度上符合了正态分布。

2.4 模型训练

将标准化处理后的特征利用支持向量机进行模型训练,核函数使用高斯核,使用网格搜索法进行超参数的优化。由于样本集较少,使用十次十折交叉验证法来避免过拟合。最终模型误差见表5。

由表5可以看出,模型误差较LightGBM模型大,但实际上却更符合实际地质情况。

表5 训练模型误差Tab.5 Training model error

3 预测结果

依据训练模型得到的预测结果如图6所示,经过了平滑处理。由图6可以看出,东南部陡坡带砂体最厚,该区域为研究区的沉积中心,也是研究区地层最厚的部分。砂体向北延伸,厚度逐渐减薄,至北部物源区又逐渐变厚。西部砂体相对较薄,西南部可见交力格地区砂体末端,被构造带所阻挡。

图6 预测砂体厚度Fig.6 Predicted sand body thickness diagram

4 讨论

4.1 算法的选择

利用LightGBM预测的砂体厚度如图7所示。为方便对比,图7与图6的色标设置相同。

图7 利用LightGBM预测的砂体厚度Fig.7 Sand body thickness predicted by LightGBM

由图7可以看出,与SVM预测结果相比,LightGBM模型预测厚度下限更高而上限更低,更靠近组中值。造成这个结果,是由于基于LightGBM的模型在包括训练集和测试集的样本集上过拟合了,因此模型在训练集和测试集上效果都很好,预测结果却不符合实际地质情况。而该现象的本质原因是样本集太小,且井位的分布范围有限,而LightGBM通过 leaf-wise(best-first)策略[25]来生长树,当样本集较小的时候,可能会造成过拟合。通常可以利用超参数max_depth来限制树的深度并避免过拟合,而研究选择利用SVM来进行模型训练,以发挥其在解决小样本问题上的优势。可以看出,基于SVM的模型在研究中表现更好,结果更符合实际地质情况。同时,虽然基于SVM的模型的误差相对较大,但制图时通常要进行平滑处理,削弱了异常值的影响,一定程度上减小了误差。因此,研究最终选择SVM算法进行砂体厚度的预测。

4.2 特征选择对比

特征选择在机器学习中有着重要意义。研究中,特征选择是指从获取的大量地震属性中筛选出一个合适的子集作为训练集和模型输入。特征选择的意义有3个方面[26]:①特征选择加快模型的训练速度。规模更小的地震属性子集可以减少运算量,因而加快模型的训练速度。②特征选择可以改善模型的性能。特征选择可以去掉无效的或者噪声特征,有些地震属性对模型训练无益甚至有害。③特征选择可以增强模型的可解释性。研究中选择的7个地震属性均与砂体厚度存在直接或间接的联系,能更好地理解模型训练的过程和结果,提高模型的说服力并找到提升模型精度的方法。一些复杂的模型(如神经网络)即使有着很高的准确性,但很难了解模型内部的细节和特征的重要性。

特征选择主要分为3类:过滤式、包裹式和嵌入式[27]。过滤式是最简单也最常用的方法,它不依赖于模型,直接将特征按照价值高低进行排序,而后选择一定数量或比例的特征进行模型训练。该方法有3种评价标准:①依据特征包含的信息量。该标准通常使用方差法来进行评估,如果特征方差较低,说明其对结果影响不大,可以舍弃。该方法需要先对特征进行标准化或归一化处理才能相互比较,以消除数量级的影响。该方法可作为数据预处理,以减少计算开销。②基于统计学理论。该标准的方法包括皮尔逊相关系数、斯皮尔曼相关系数等,根据计算结果确定相关性。③基于信息论。该标准的方法包括互信息、最大信息系数和Copula熵等,同样根据计算结果确定相关性。过滤式方法不依赖于模型,因而无法针对特定模型选择最合适的特征子集。同时在评价相关性时,特征之间相互独立,一些相关性低但组合使用具有较高价值的特征会被舍弃。另外,保留特征的数量或比例也需要根据经验或结果来调整。

包裹式方法是对于某一模型,在所有特征中选择效果最好的特征子集,因为其计算量巨大,通常使用序贯选择或启发式算法,以减少计算开销。但无论哪种方法,其计算开销依然很大。

嵌入式方法是在训练模型的同时完成特征选择,该方法包括基于L1正则化的特征选择和基于树模型的特征选择等。该方法有着过滤式和包裹式二者的优点,依托模型进行特征选择的同时,大大减少了计算开销。

本研究使用的LightGBM就是基于树模型的框架。本工区地震资料品质低,地震波主频为18 Hz左右,因此计算得到的地震属性质量较差,各个地震属性与砂体厚度的各种相关系数都不高。研究所选特征的部分相关系数见表6。可以看出,绝对振幅积分、相对层厚度、弧长等属性具有较高相关性,而其余属性,尤其是单频振幅_30的相关性较低。如使用过滤式方法,前者会被选中,而后者会被舍弃。然而,后者在模型中也有着重要作用,如果舍弃会造成模型性能差。这说明了嵌入式方法的优越性。

表6 所选特征的部分相关系数Tab.6 Part of correlation coefficient of the selected feature

4.3 研究的缺陷与改进

如上文所述,研究区地震信号主频在18 Hz左右,地震资料品质低、分辨率差,影响了地震属性的提取结果,进而影响了模型的预测精度。因此,若能提高地震资料的分辨率,如反Q滤波法[28],则可以进一步提高预测精度。

研究的目标层段为九佛堂组的湖侵体系域,工区并没有对九佛堂组进行进一步的层序划分,这在一定程度上影响了地震属性的提取,进而影响了预测精度。

5 结论

单一地震属性在预测砂体厚度时具有多解性,难以进行准确预测。研究提出了基于LightGBM和SVM的地震多属性砂体厚度预测方法,并通过对陆东凹陷前后河地区九佛堂组湖侵体系域的实际应用,验证了该方法的可行性。结果表明,相比于常用的过滤式特征选择方法,基于嵌入式的特征选择方法得到的特征子集有着更好的效果。同时,基于SVM算法的模型在小样本的条件下表现更好,结果更符合实际地质情况。因此,通过联合LightGBM和SVM算法,可以有效提高砂体厚度的预测精度。