基于图卷积和注意力机制的高速公路交通流预测

冯凤江，杨增刊

(1. 河北上元智能科技股份有限公司，河北 石家庄 050000；2. 河北庆恒科技发展有限公司，河北 石家庄 050000)

0 引言

高速公路管理控制的基础之一是短时交通流预测[1-2]，近年来大数据挖掘驱动方法研究已成为其主要方向[3-7]。高速公路不同于城市道路，其管控实施效果存在滞后性，如相邻上下游匝道间距离较远，若下游较远路段出现拥堵，则匝道调节效果需较长时间才能发挥作用，使高速公路控制措施必须适度提前，多步预测成为高速公路控制工程应用的必要条件。理论研究方面，早期高速公路交通流预测集中于使用自回归滑动平均、卡尔曼滤波等统计模型方法，而后预测集中于使用人工神经网络、支持向量机、非参数回归等浅和深层神经网络的机器学习方法[1-2，8-11]。这些方法虽有各自特点和优势，但在多步预测时偏差较大，难以满足工程需要，且大部分方法使用时仅利用预测断面或路段数据，没有利用可能影响预测路段流量的其他路段数据，尤其是高速公路上游和可能反向传播的下游数据，无法体现交通流的空间分布特点。

编解码序列对序列(Sequence to Sequence，Seq2Seq)结构由于能够提供一个输入输出序列可不等长的框架，近年来被广泛应用于机器翻译领域，是研究深度学习的主要方法之一[5，12-13]，特别在多步预测方面可取得较高精度。其中注意力机制加入编码层后[12]，给每一个输入数据分配权重，使解码时能选择与预测目标值权重更大的元素从而提高预测精度[12]。在基于注意力机制的Seq2Seq多步预测模型中，输入序列的选择和特征提取是预测结果是否达到高精度的关键，例如通过正反向学习时间依赖关系，避免信息丢失的双向长短期记忆(Bi-directional Long Short Term Memory，Bi-LSTM)网络模型[6]，将输入门和遗忘门合为一体只保留更新门和重置门的双向门控循环单元(Bi-Gated Recurrent Unit，Bi-GRU)模型[12-15]，通过其双向门处理得到有效信息，克服传统机器学习在处理长期依赖问题时存在的梯度消失和爆炸问题，提升运算精准性，并由于比其他方法所需神经单元数量少，效率更高，稳定性更好，更容易进行训练，成为了深度学习多步预测特征提取中的最新方法，被应用于城市轨道交通、道路交通流速度的多步预测中[3，12-14]。但这些研究对象不涉及高速公路断面交通流参数预测，高速公路空间分布和预测模型融合尚需深入研究。

将交通流空间分布特点参数和可能影响预测点的其他路段时间分布参数(时间序列)融入到预测模型中是近年来交通流预测的一个新趋势，如陈喜群等[16]提出一种基于图卷积网络(Graph Convolution Network，GCN)的城市路网短时交通流预测模型；Zhang等[3]提出一种注意力图卷积(Attention Graph Convolution，AGC)Seq2Seq深度学习模型来获取交通流空间和时间相关性，提升多步预测的精准度。这些研究较少涉及双向注意力机制，研究对象也不面向高速公路。基于此，本研究提出一种考虑时空分布的高速公路交通流多步深度学习预测方法，结合路网结构提取预测路段和“可能影响上下游的其他路段”的空间特征，将融合后历史和实时时间序列数据作为输入，建立图卷积神经网络和注意力机制融合的高速公路交通流多步预测模型Bi-GRU-Seq2Seq，通过试验予以分析验证。

1 预测系统结构

高速公路交通流预测系统依托道路拓扑结构，由信息采集子系统、数据库、知识库、预测模块等组成，系统结构如图1所示。其中：(1)高速公路网络表示为G(V，E，A)，V为节点集，取检测器所在的主线门架、出入口匝道门架、立交桥门架等位置；E为边集，e为每一条边点间的路段(基本单元)；A∈RN×N为G的邻接矩阵，aij为其元素，其值为1时表示路段ei和ej连接，为0则表示不连接。(2)预测对象为网络中每一个路段(边)或节点在未来时间段的交通流参数估计值，如主线断(截)面流量、路段流量或密度、速度等。

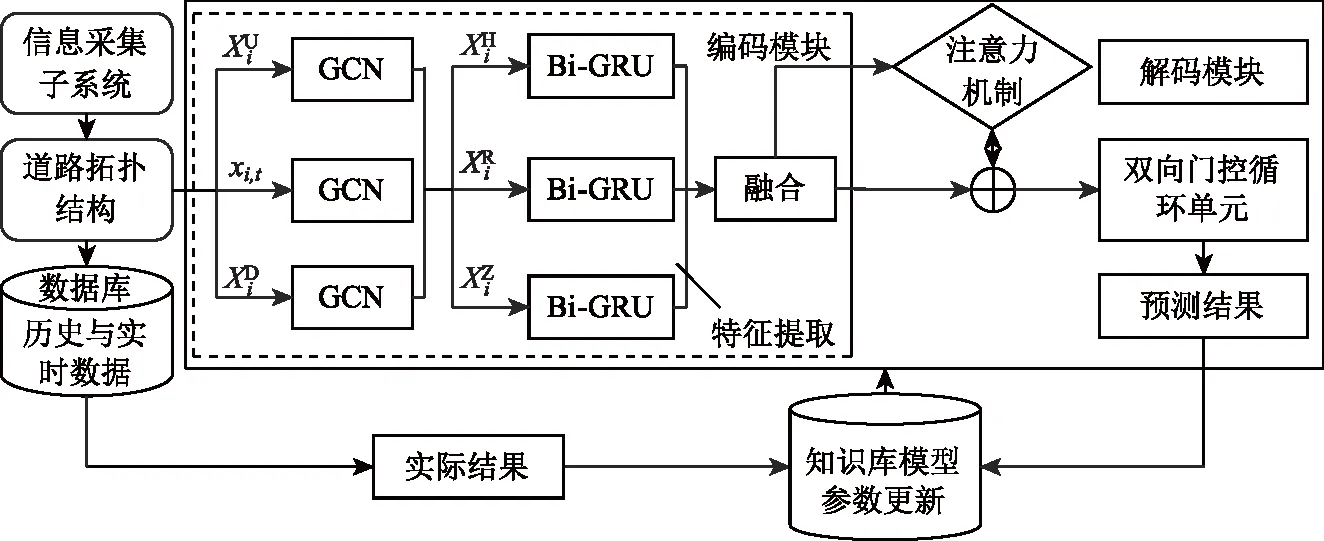
图1 预测系统结构Fig.1 Structure of prediction system

1.1 预测系统原理

预测系统基本原理为：

(1)由信息采集子系统采集的实时交通流信息存储在数据库中，并计算处理供系统使用。

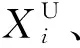
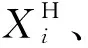
(4)采用注意力机制获取各特征值的权重，将提取的包含空间特征的时间序列数据加权融合后带入GRU模型，得到路段交通流多步预测值。

(5)将预测值和随后采集到的交通流实时值存入知识库中，更新预测模型中相关参数值。

1.2 预测路段(断面)空间数据选取

断面i交通流参数影响其未来l个时段预测值Xi，t+l=(xi，t+1，xi，t+2，…，xi，t+l)T∈Rl的空间数据为：

(1)上游路段。考虑到高速公路各路段(基本单元)较长，对于短时交通流预测，只有“车辆以最大速度抵达被预测路段的”上游路段的交通流参数对预测产生影响，本研究对受到影响的上游路段数u1定义为：

vmax，i-1，i-2+li-1，i/vmax，i-1，i)>=T·k]，

(1)

(2)下游路段。下游出现拥堵时主线出现反向传播情景，从而影响预测截面i的交通流参数，对于预测第k步参数xi，t+k，可能影响预测断面的下游路段数u2定义为：

li+u2-1，i+u2/wmax，i+u2-1，i+u2)>=T·k]，

(2)

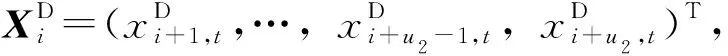
1.3 预测路段时间数据选取

预测路段时间数据分为时间临近性特征参数(实时数据)和周期性特征参数(历史数据)两部分：

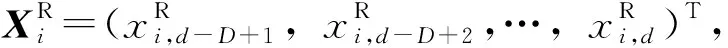
2 基于注意力机制交通流的Seq2Seq预测模型

2.1 特征提取

(1)空间特征提取。采用GCN方法进行空间特征提取[4，17-18]，利用K阶邻域矩阵对第1节中所述高速公路网络中的每个截面流量数据的时空进行融合。对于截面i可能受到的上下游空间影响路段数u1和u2，定义其K阶路段集合为λi(K){j∈[i-u1，i+u2]}。为模仿拉普拉斯矩阵，对于邻接矩阵A添加单位矩阵I，其K阶邻域矩阵可通过计算A+I的K次幂得到：

(3)

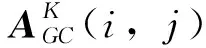
(4)

对可能影响本路段的上下游时间序列进行图卷积操作，通过下式完成全部截面信息更新：

(5)

式(5)中截面i的更新过程见式(6)：

[xi，t-n+1，…，xi，t]，

(6)

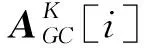
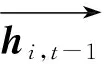
(7)

(8)

(9)

(10)

式中，GRU(·)为非线性映射函数，为t-1时段正反向隐藏层状态；Vt，V′t，bt分别为t时段网络自学习的正反隐状态权重和偏置。式(8)～(10)分别表示临近、日周期、周周期的时序特征，将以上Bi-GRU的输出进行加权融合，得到综合时间序列特征：

Hf=WhHh+WrHr+WzHz+bf，

(11)

式中，Hf为融合后影响因素状态集合；Wh，Wr，Wz，bf分别为各自特征的权重及偏置；Hh，Hr，Hz分别为临近、日周期、周周期时序特征中不同时间段隐层状态的集合。

2.2 预测模型输入(特征向量)计算

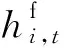
(12)

(13)

(14)

2.3 预测值计算

将解码器上一时段预测值xi，t+l-1、隐藏状态si，t+l-1和当前时段的注意力向量ci，t+l作为GRU模型的输入来更新当前时段交通流隐藏状态，经过vy线性变换得到当前交通流参数预测值：

si，t+l=f1(si，t+l-1，xi，t+l-1，ci，t+l)，

(15)

(16)

式中，f1为解码器GRU模型的非线性映射函数；by为模型自学习的偏置。

2.4 模型参数动态更新

对于第l步的预测值x′i，t+l，使用均方根误差(RMSE)最小化为预测模型参数确定和动态实时更新的依据，具体采用Adam优化器梯度下降法进行迭代训练：

(17)

第t步预测模型参数θt更新步骤为：

(1)计算第t步梯度gt。

(2)计算gt指数移动平均mt和纠偏值m1t，其中为β1梯度指数遗忘因子或衰减率：

mt=β1mt-1+(1-β1)gt，

(18)

(19)

(3)计算gt平方的指数移动平均vpt和纠偏值vp1t，其中β2为梯度平方的指数衰减率：

(20)

(21)

(4)更新参数：

(22)

式中，α为学习率；ε为避免除数变为0的设置数。

3 应用分析

3.1 试验背景

以京港澳高速涿州—保定北为试验对象，该段含6对出入口匝道和2个与其他高速互通的立交桥，主线单向4车道，长度为76.4 km，大车限速值为100 km/h，小车限速值为120 km/h，反向传播速度为25 km/h。依据设置在门架上的视频检测器、各匝道出入口和互通式立交桥进行基本单元(路段)划分，如表1所示。数据由高速公司通过视频软件处理提供，2020年10月至12月间，前49 d为训练集，后14 d为测试集。断面交通上下游影响分别按车辆最大限速和反向传播速度计算确定，如徐水断面预测粒度为20 min 时，上游对其影响最大长度为40 km，至廊涿立交，取4段路(基本单元)，长度分别为14.2，2.8，4.3，13.7 km；下游对其影响最多8.4 km，至保津互通，取1段路(基本单元)，长度为16.2 km。

表1 路段划分和长度(单位：km)Tab.1 Section divisions and lengths (unit：km)

试验基于Pytorch框架，采用32个大小相同的卷积核计算，其中批大小为64，学习率为0.001，Dropout为0.5，迭代100次，并将数据进行Min-Max归一化处理，预测未来时段长度Tp设置为0.5 h，例如2020-11-26T08：00—08：25，历史数据中分别设置h，r，z为6，2，2，如图2所示，其中Th为当前时段前3 h，Tr为前2 d相同时段，Tz为前2周相同时段。

图2 预测模型中输入输出示范Fig.2 Demonstration of input and output in forecasting model

3.2 试验结果及分析

以2020年11月26日徐水门架断面为例，图3(图中 0为时间08：00)为采用不同时间粒度的2步流量预测值与真实值对比，图4和5分别为自由流和拥堵下多步流量预测值与真实值对比，其中步长为1～4步，预测效果评价指标为平均绝对误差(MAE)、均方误差(MSE)和平均绝对百分比误差(MAPE)。可以看出：

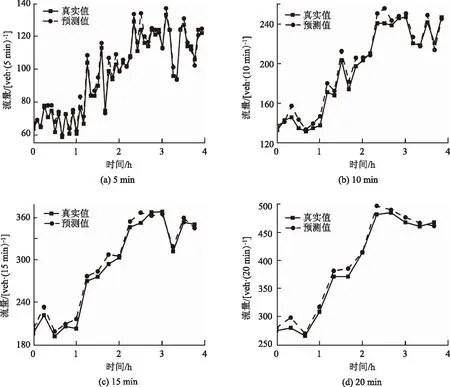
图3 不同时间粒度预测值与真实值对比Fig.3 Comparison of forecast and actual values at different time intervals

图4 自由流状态下预测指标对比Fig.4 Comparison of forecast indicators in free flow state

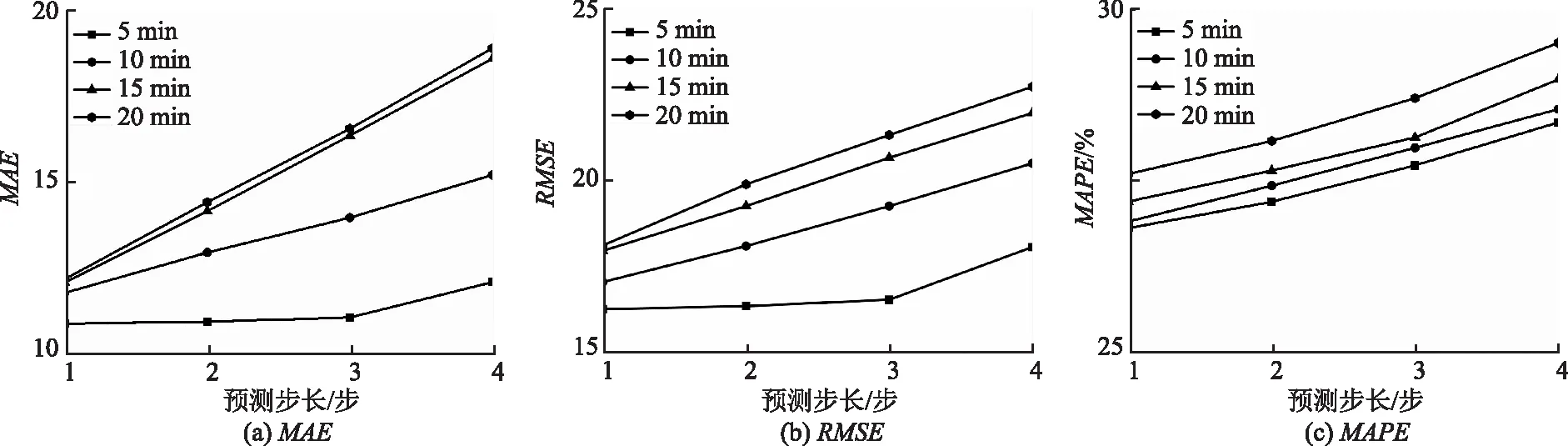
图5 拥堵下预测指标对比Fig.5 Comparison of forecast indicators in congestion state

(1)预测值和真实值之间偏差较小，预测拟合曲线基本反映了未来一段时间交通流的变化趋势，表明了本研究交通流多步预测方法的适用性。同时由图3～5可看出，随粒度的增加，预测精度稍显下降，这是因为随时间粒度的增大，交通流间差异性降低，进而模型捕获交通流时空差异性的能力逐渐减小所致。

(2)预测精度随着预测步长的增加逐渐减小，这是因为本研究交通流多步预测步长均不小于5 min，精度得到了保障。但作为高度非线性系统，随着预测步数的增大，后续趋势是否发生转变，只能依据原有趋势进行外推。而多步预测方法由于充分利用注意力机制和Bi-GRU捕获时间特性，采用图卷积充分捕获空间影响的特性，捕捉交通流时空差异性，较好地依据当前状态预测未来短期趋势，偏差较小，且时间粒度为5～10 min时，3步内的预测结果均在合理范围内。

(3)不同交通状态对预测精度产生影响。不同状态下随着预测步长的增加，评价指标均呈增加趋势，验证了“预测是利用原有趋势外推，误差会逐渐增加”的现象。自由流状态各指标值均小于拥堵交通状态下各指标值，这是因为交通流作为时空分布不均衡的高度非线性系统，拥堵下交通流波动较大，增加了预测的难度。虽然精度降低，但由于本研究多步预测方法充分考虑时空特性，很好地适应交通波动，预测精度依然在合理范围内，无论是一般状态还是拥堵状态，短时交通流预测均能取得较高精度，满足实时管理控制需要。

3.3 与其他方法对比分析

以5 min为时间粒度进行不同预测方法对比试验，其中方法1为本研究交通流多步预测方法；方法2为“不考虑上下游路段，其他模型计算同本交通流多步预测方法”，本研究简称为不考虑空间特征方法；方法3为采用图卷积注意力模型的方法；采用Seq2Seq模型为方法4。图6和7分别为自由流状态和拥堵状态下的流量预测值与真实值对比。可以看出：

图6 自由流状态下不同方法预测指标对比Fig.6 Comparison of forecast indicators in free flow state with different methods

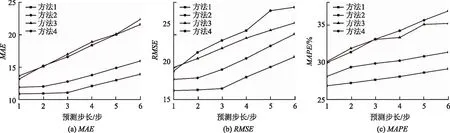
图7 拥堵状态下不同方法预测指标对比Fig.7 Comparison of forecast indicators in congestion state with different methods

(1)在各种预测方法中，无论是不同的预测步数，还是交通流处于何种状态，基于深度学习的方法1和2精度高，而方法3和4没有综合各种深度学习的优缺点，使其精度较低，特别是在多步预测时。

(2)本研究方法预测精度最高，这是因本研究方法不仅利用双门控循环单元提取时间特征，还考虑了上下游影响范围并利用图卷积网络提取空间特征，更好地挖掘交通流量时空特性，使预测模型更能高度映射内部的非线性关系，能够满足工程实际需要。

(3)随着预测步数的增加，本研究方法误差增长趋势更加缓慢，这是因深度学习并非要学习更多的数据信息，无用信息过多反而会影响模型精度。利用最大限速和反向传播速度计算得到上下游影响范围，将其作为预测模型的输入。同时基于注意力的Seq2Seq策略取得精确的权重值，提升了多步预测精度，进一步显示了本研究方法在多步预测中的优势。

4 结论

综合交通流空间分布特征和周期性特点，建立了高速公路短时交通流Bi-AGCGRU-Seq2Seq多步预测模型，通过试验予以分析验证，证明了本研究交通流多步预测方法的有效性并能够满足多步预测精度的要求。本研究仅是高速公路交通流预测的初步研究，尚需针对拥堵下交通流非线性特点，结合其波动大的特征研究进一步提高预测精度的改进方法，以期对高速公路拥堵下的预判及控制提供决策支持。