基于驾驶人有限理性的交织区换道行为决策
2023-11-15车松珊钱勇生曾俊伟魏谞婷
车松珊,钱勇生,曾俊伟,魏谞婷
(兰州交通大学 交通运输学院,甘肃 兰州 730070)
0 引言
随着道路系统不断发展,路网结构不断精密,匝道、互通式立交和交叉口的数量急剧上升,越来越多由两股或多股车流组成的交织区域成为道路系统的重要瓶颈路段,其交通紊乱状态远高于其他基本路段。研究表明,制订交织区交通控制策略不仅可以改善交织区内部交通状况,还可以大幅提高整个路网通行效率[1],精确揭示交织区的交通运行特性是检验管控效率的有效途径。
近年来,国内外学者针对交织区交通流较为常见的分析方法包括回归分析法、理论解析法和微观交通流仿真等。回归分析法通过采集区域交通流数据,进一步建立评价指标和拟合模型,如孙剑等[2]通过对HCM各版本模型分析,新增了重要因素的函数形式,提出了改进的回归模型,用于交织车辆和非交织车辆的速度预测,该方法虽简单、直观,但需采集大量有关数据进行统计,模型普适性较差且不利于分析车辆行为特征;以间隙接受模型为代表的理论解析法,最初由Lertworawanich等[3]等利用线性规划的思想,计算不同类型交织区的通行能力;Xu等[4]应用可接受间隙模型融入车道变化中预测实时最大流量,但该类模型存在较多假设前提,计算复杂,由于简化了交通运行规则,不易反映交织区交通流运行特性。随着计算机技术的蓬勃发展,仿真手段具有更强的可操作性和可拓展性。对于交织区域,复杂的车辆行为是导致交通紊乱的直接原因,其中元胞自动机(Cellular Automata,CA)作为一种微观离散的仿真方法,成为分析、模拟交通流车辆动力学行为的主要手段。Xiang等[5]修改了换道规则,引入动态换道概率,提出了BL-STCA模型;潘守政等[6]将换道行为进一步划分,探究交通波的同步机理;Kong等[7]考虑对不同车辆驾驶行为的差异性,构建改进的元胞自动机模型;谢济铭等[8]基于Gaussian分布模型的换道概率提出交织区域分区CA模型。
然而针对交织区交通流建模研究中,考虑到驾驶决策者由于个体属性、心理特征、对行驶环境感知的不同,跟驰和换道行为均表现出较大差异。Ni等[9]基于连续分布函数,制定CA模型中车辆加速度规则;马新露等[10]引入驾驶决策者特征参数,建立驾驶行为异质性的合流区仿真模型,但其中建模思想都将决策者视为完全理性行为,无法反映决策者的主观偏好和风险态度。针对上述问题,本研究提出了一种基于前景价值理论的交织区交通流建模方法,利用价值函数的结构特征体现驾驶决策者偏好的不确定性,此外考虑动态的换道意愿和预估车速进行模拟交织区域交通流现象的演化机理,为交通仿真和人车路协同优化提供理论和技术支持。
1 基于轨迹数据的交织区换道行为特性
交织区是在没有交通设施控制的情况下,两股或多股车流沿着相同的行驶方向进行交通流的交叉。本研究以目前常见的高速公路交织区类型—同侧A型交织区为例进行研究,因此采用美国联邦公路局开发的新一代微观仿真系统所提供的NGSIM数据集,选取其中US-101路段交织区的车辆行驶轨迹对驾驶行为特性进行分析。US-101路段采集长度约为640 m,包括5条主车道、1条辅道连接匝道汇入车道和汇出车道[11]。数据由车辆位置、速度、加速度、车型等信息组成,时间精度为0.1 s。
1.1 数据预处理
由于高空视频采集过程中受环境、测量仪器结构等检测因素影响,实际数据与公布的轨迹数据存在一定偏差。为降低该误差对分析结果的影响,采用对称指数滑动平均(Symmetric Exponential Moving Average,SEMA)滤波算法对数据进行降噪处理[12],即在固定的平滑窗口中进行加权平均计算,具体算法如式(1)~(2)所示:
(1)
m=min{3T/dt,i-1,Nn-i},
(2)
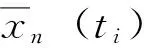
1.2 换道行为特性分析
因交织区中存在大量的汇入汇出行为,且驾驶人个体间差异化特征导致对换道环境的决策相差较大。驾驶人在换道决策前为避免潜在的冲撞风险,需考虑目标车道的前后车辆与本车辆的相对间距和速度。以轨迹数据中换道间距为例,为保证聚类算法对换道间距决策的准确性,基于NGSIM数据集车辆的实时轨迹,在车辆改变车道号前选择最近的一个横向加速度为0且之前的加速度方向与换道方向不同的点定义为换道起始点,统计此时换道车辆与目标车道相邻前车间距、后车间距,如图1所示。
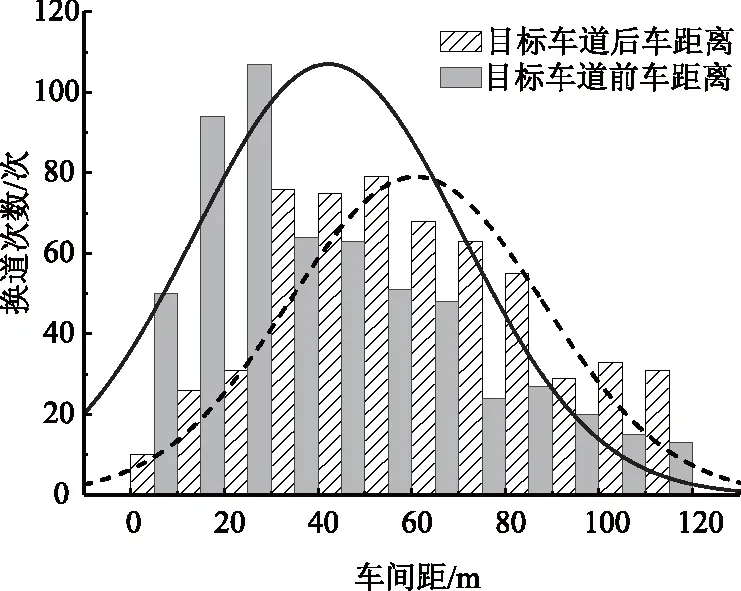
图1 换道间距统计图Fig.1 Statistical diagram of lane-changing spaces
选用模糊C-means算法对换道行为特征进行聚类分析。当目标车道相邻前后车间距均较大时,换道车辆无碰撞风险,此时难以体现驾驶人的行为差异特征。因此,本研究选取换道车辆与目标车道前车间距或后车间距较小的3种换道场景进行划分驾驶风格,其核心目标函数算法为:
(3)
式中,n为样本数;k为聚类中心;U=[uij](1≤i≤n,1≤j≤k)为隶属度矩阵;m≥1为模糊加权指数,用来控制隶属度的影响。聚类结果如图2和表1所示。
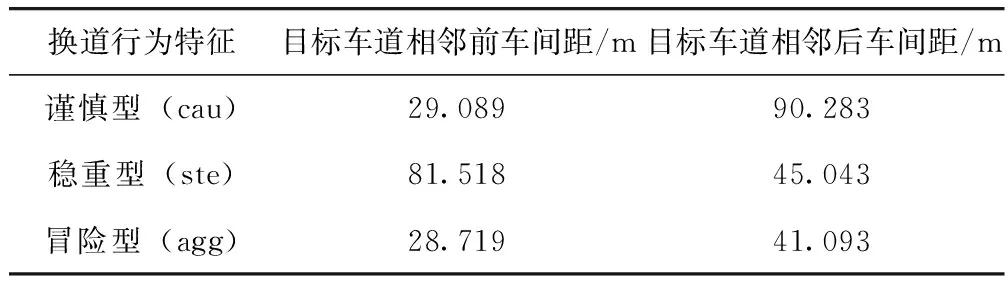
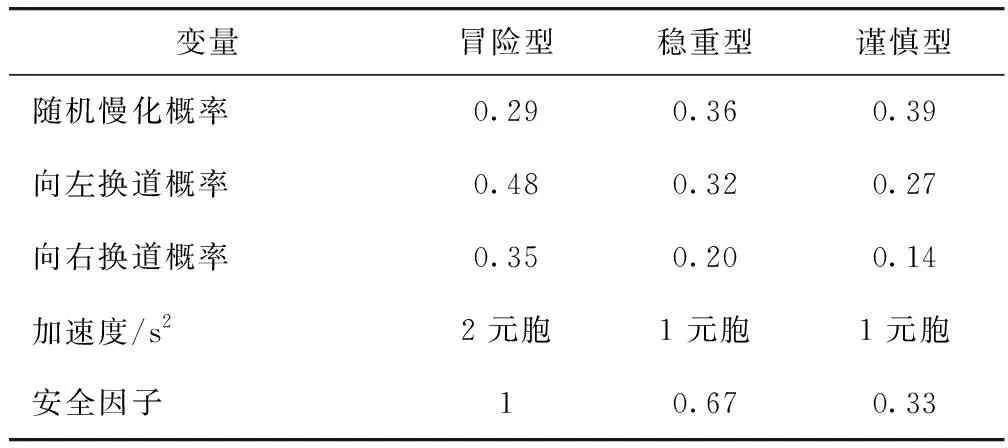
表1 模糊聚类结果分析Tab.1 Analysis of fuzzy clustering result
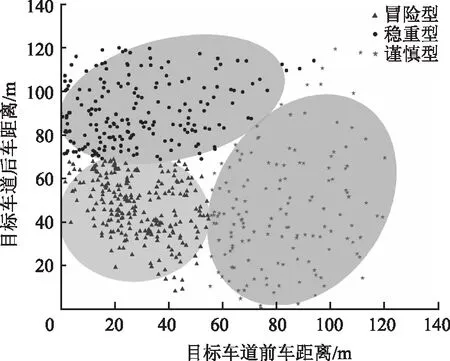
图2 FCM聚类分析结果Fig.2 FCM cluster analysis result
根据以上聚类结果可以看出在交织影响路段驾驶人个体差异对换道环境的选择影响较大,对此将驾驶人进行风格划分,匹配对应的驾驶行为,划分方式如下:
(1)对于谨慎型驾驶人。与目标车道前车间距较为离散,偏好与目标车道后车间距远大于其他类型驾驶人,此驾驶行为可以最大限度地控制换道带来的安全风险。
(2)对于稳重型驾驶人。相较于目标车道后车的安全间距,更关注与目标车道前车的行驶间距,在保证换道的基本安全条件下,崇尚较大的目标车道可加速空间。
(3)冒险型的驾驶人。在交织区域换道中较为常见,由于具有频繁汇入汇出主线的需求,往往在换道时与目标车道相邻前后车间距均较小,存在较大的安全风险。
为更精确地模拟交织区交通流现象,需针对驾驶人个体差异的不同进行交通流模型的建立。
2 仿真模型构建
经典的交通流仿真模型在换道时侧重于考虑速度-间距关系,较少针对人为的换道决策过程、驾驶人的个体差异及间距分布等展开研究。而现实环境中,驾驶人面对实时交通信息时无法采取一致无偏方式进行处理,其中对于信息的过度反应或反应不足即是有限理性驾驶行为导致[13]。因此,本研究基于不确定的驾驶行为特征,建立了考虑驾驶人有限理性的多车道交织区元胞自动机模型。由图3所示的仿真场景可见处于车道i的第j辆车与周围车辆的行驶环境。

图3 多车道交织区换道主要影响因素示意图Fig.3 Schematic diagram of main influencing factors of lane-changing in multi-lane weaving area
2.1 基于前景理论的换道行为建模
车辆在交织区的换道行为存在多元的换道需求和换道意愿。驾驶人在换道决策过程中主要受本车与邻近车辆的速度差与间距差等因素影响,进行综合决策。但目前研究多集中于驾驶人的完全理性行为,无法表现出个体差异间大换道间距被拒绝,小换道间距被接受等交通流现象。不同驾驶人面对收益和损失具有差异化的处理态度,在此不确定性条件下,本研究以有限理性理论为基础,采用前景理论的价值函数,模拟驾驶人对动态换道间距的决策过程。
2.1.1 改进价值函数
考虑到一般情况下决策者面对收益时表现为风险规避,面对损失时表现为风险偏好,原前景理论价值函数呈现“S”形曲线且决策者的风险态度系数只能取0<α,β<1。但在实际道路交通中存在大量异质性的驾驶行为,因此扩大α和β的取值范围以适应不同类型驾驶人的心理决策特性。如图4所示,将0<α,β<1扩展到α和β等于1,α和β大于1,分别对应不同类型驾驶人的有限理性决策行为,改进的价值函数如下所示[14]:
(4)
式中,λ为损失规避系数,表示决策者对损失的敏感度。xo为决策者的心理参考点,当xi-xo≥0时,表示决策者获得的收益;当xi-xo<0时,表示决策者获得的损失。α和β为风险态度系数。
2.1.2 车辆换道规则
(1)换道动机产生。车辆在交织区域的换道需求相比于普通车道更为复杂。当车辆受到前车阻挡,产生换道动机如式(5)~(6)所示:
(5)
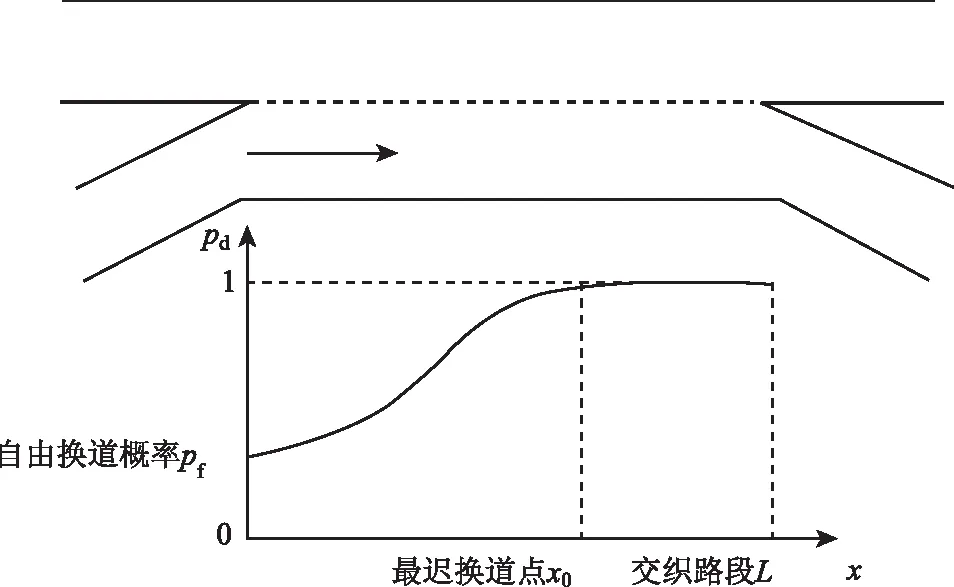
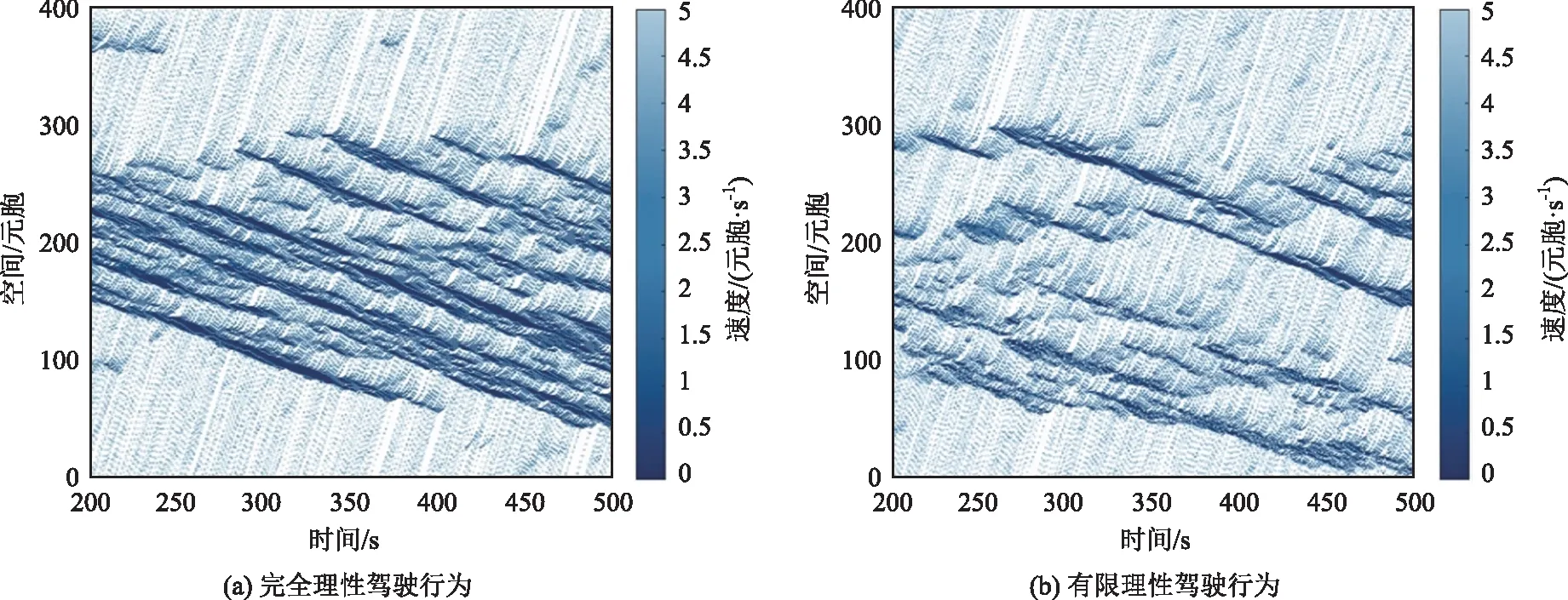
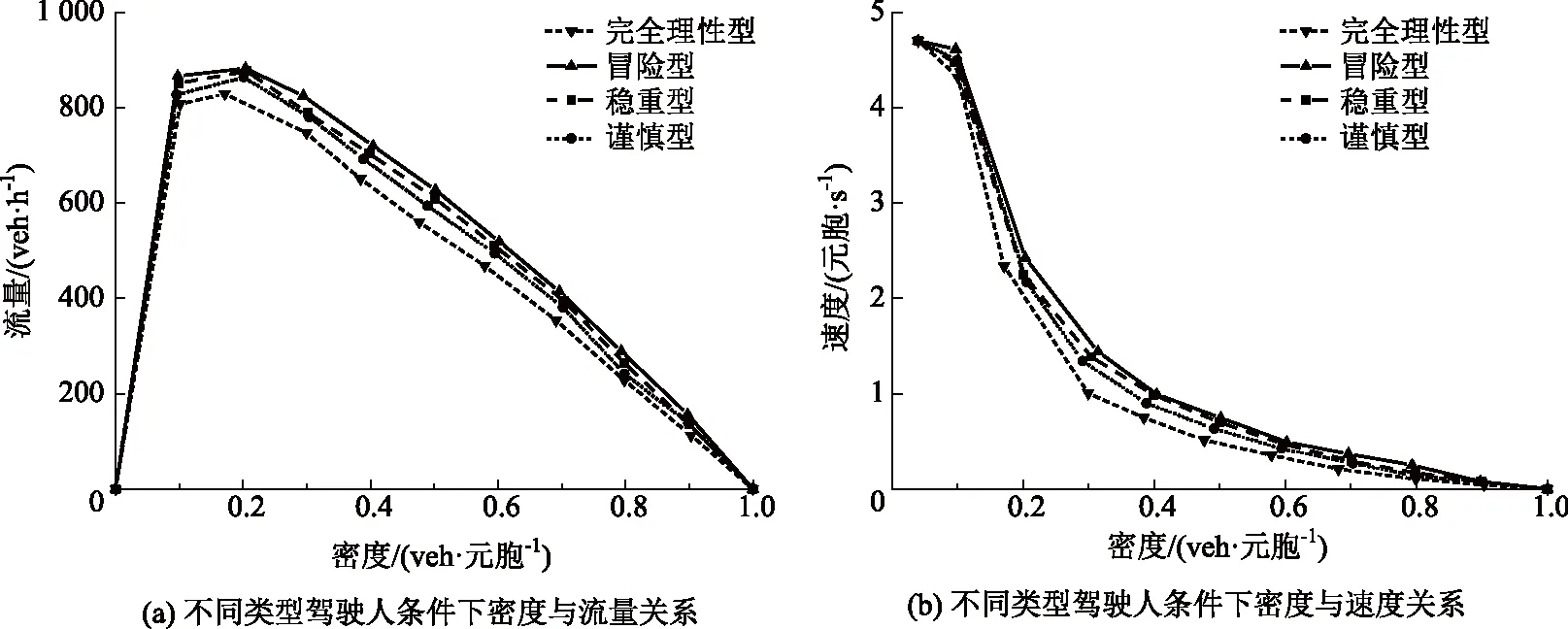
vi,j+1(t) (6) (i,j)位于主线&rand(0,1)<ψ1, (7) (i,j)位于匝道&rand(0,1)<ψ2。 (8) (2)动态换道间距感知建模。为模拟不同驾驶人对换道环境决策的差异并区别于以往研究中的完全理性个体,交织区内车辆需要在有限的距离内换至目标车道。因此,根据价值函数曲线构建驾驶人对于动态换道间距的感知效用,参考以往文献中保守的换道条件,选取vmax作为参照点[15],驾驶人对于目标车道前后间距的感知偏差如式(9)~(10)所示: (9) (10) 当Δx1和Δx2>0时为收益区间,无论驾驶人性格差异都会采取换道措施,而当Δx1和Δx2≤0时为损失区间,在此较小的换道间距中,不同类型的驾驶人对换道决策的判断具有较大差异。由此,构建有限理性的换道安全条件如式(11)~(12)所示,向右换道为: (11) 向左换道为: (12) (13) 式中通过调整风险态度系数β和损失规避系数λ可模拟不同类型驾驶人特性,当β和λ等于1时,即为STCA-I换道规则。 (14) (15) 图5 强制换道概率走势图Fig.5 Trend chart of forced lane-changing probability (4)换道执行。在自由换道条件下,车辆根据向左和向右换道概率建立换道执行条件如下: 具有汇入汇出主线需求的车辆,换道执行条件为: 基于驾驶行为特征的差异性建立预估前车动态速度的跟驰模型,通过引入安全因子γ∈(0,1)来刻画驾驶人的冒险程度。对于不同类型驾驶人在计算与前车行驶的安全间距时不再将其视为静止粒子而是会考虑前车的动态预估车速,由此反映跟驰行为的心理特征。 (1)加速规则:反映车辆在跟驰行为过程中驾驶人对于更高行驶速度的追求。 (16) (2)安全防护:当车辆与跟驰前车行驶间距小于安全间距时,为了避免碰撞而进行的确定性减速。 (17) (3)随机慢化:由于实际交通存在不确定的驾驶行为,可能导致车辆减速,因此引入随机慢化概率pslow对车辆进行不确定性减速操作。 vi,j(t+1)→min[vi,j(t)-rand(0,ai,j),0]。 (18) (4)位置更新:获得车辆速度后,对其行驶位置进行更新。 xi,j(t+1)→xi,j(t)+vi,j(t+1), (19) 式中γvi,j+1(t)为异质驾驶人预估与跟驰前车的动态间距,其中γ值越大,车辆跟驰时与前车的间距要求越低,意味着驾驶人更为冒险,γ值越小,车辆跟驰时与前车的间距要求越高,驾驶行为更偏谨慎。通过上述改进,弥补了传统跟驰模型无法模拟驾驶行为的差异化,同时又确保了车辆行驶过程中的安全性。 表2 模型参数初始化Tab.2 Initialization of model parameters 对交织区域内驾驶行为的有限理性进行时空分析,以交织现象最凸显的车道3为例绘制速度—时空分布图,如图6所示。其中图6(a)是在驾驶人均为理性驾驶人的条件下,采用STCA模型的时空分布情况;图6(b)中采用文献[17]符合现实情况的驾驶人类型比例pagg∶pste∶pcau=0.2∶0.5∶0.3,以改进后的考虑驾驶人有限理性交通流动力学模型为场景。 图6 速度的时空分布图Fig.6 Spatio-temporal distribution of velocities 图6中不同的色度值代表车辆速度的大小差异,可看出在相同的车辆密度条件下,2种仿真场景具有明显差异的时空状态。在图6(a)中,100~300元胞的交织区域出现了较多的局部堵塞,交通流频繁呈现自由流与拥堵流的转换,且拥堵范围在进行反向传播的过程中持续时间更长,如223元胞、275元胞等多处空间位置。这是由于交织区域本身具有大量的换道行为,而完全理性驾驶人只采取固定的换道间距和换道概率,造成该区域频繁的交通震荡现象。由图6(b)可知,考虑驾驶人为有限理性后堵塞现象大幅度减少,局部小范围拥堵流更快速产生相变,交织区域内色度值整体变浅。这是因为改进后的模型考虑了驾驶人的风险偏好,引入了动态换道间距感知,可根据行驶环境实时调整换道决策,有效地减少堵塞带的传播现象。 换道特性是描述交织区域交通流的重要特征,对不同类型驾驶人在各车道100~300元胞的换道频率分布进行统计分析。在不同的仿真情形下,为消除强制换道的差异化影响,初始化时将出入匝道的车辆进行平均分布,仿真输入车辆的总占有率为0.2,得出驾驶人的异质性对交织区域换道分布特性的影响。如图7所示,(a1)和(d1)为完全理性型驾驶人,(a2)和(d2)为谨慎型驾驶人,(a3)和(d3)为稳重型驾驶人,(a4)和(d4)为冒险型驾驶人。 其中图7(b)和(c)的第一个换道集中区域主要为车道2向车道3的换道频数和车道3向车道4的换道频数,通过横向整体比较可得:从内侧车道换至外测车道的换道集中区域位于交织区域中心位置偏左,而对于外侧车道换至内测车道的换道集中区域大多位于交织区域中心位置偏右,说明由于驾驶人递进的换道意图,使得汇入匝道的交织车辆倾向于提前换道,车道3尤为明显。针对不同类型驾驶人的换道特征,通过纵向比较可得:驾驶人的激进程度越大,各车道的换道集中区域均不同程度地向上游移动,由此说明,随着价值函数中风险态度系数β和损失规避系数λ的减小,可使不完全理性驾驶人在换道过程中冒险程度相应增大,选择与之对应的换道安全间距越容易,可避免车辆大幅度拥挤在最迟换道点附近,减少局部拥堵的产生。 为研究不同密度下驾驶人异质性对交织区域交通参数差异化的影响,根据各类型驾驶人设置相应的仿真环境。由于采用周期性边界条件,在仿真试验的任意时刻,车道中车辆总数并不发生变化,得到不同类型驾驶人的流量-密度折线图和速度-密度折线图,如图8所示。 图8 密度与流量及速度关系Fig.8 Relationship of density with flow and speed 由图8(a)可知,当车流密度K<0.12的条件下,交织区交通流以较大的斜率快速增大流量,且驾驶人特性对流量Q的影响较小;当车流密度K>0.8的条件下,流量随着密度的增加已近似重合。这是因为在低密度的自由流下,由于车辆间行驶间距较大、换道次数较少,所以无论是否考虑驾驶人此时的有限理性和对前车的预估车速,对整体交通流的影响并不大。而在高密度的阻塞流中,车辆间行驶间距较小,平均速度低,各类型驾驶人均无法很好地获取相对应的安全换道间隙,以此寻求换道得到更大速度或提前进入匝道。对于车流密度0.12 由图(b)可知,当处于自由流时(K<0.12),车辆间速度整体差距不大,平均速度约为128 km/s。随着密度增加,车辆的平均速度整体呈现下降趋势,但由于驾驶人的类型不同,趋势存在较大的差异性。在同一密度下速度随着驾驶人的冒险程度增大而增大,且考虑驾驶人的有限理性相比完全理性型,速度增长尤为明显。 针对交织区域换道过程的行为特征及驾驶人不确定的决策行为,本研究结合前景理论等方法提出了一种基于有限理性的交织区动力学模型,并据此进行了仿真试验,主要结论如下: (1)与固定换道概率的交通流动力学模型相比,对具有汇入汇出主线意图的驾驶决策者建立递进的换道意图,使得交织区域呈现出正态的换道分布,能有效展现车辆在交织区不同位置的换道强度。 (2)与完全理性交通流动力学模型相比,采用考虑驾驶人有限理性动力学模型模拟驾驶决策者对于换道过程中动态间距的感知,并结合跟驰心理行为考虑了前车动态预估车速,使得存在大量换道行为的交织区域仿真结果更加合理,有利于驾驶决策者做出真实的心理决策。 (3)与同质驾驶行为的交通流动力学模型相比,通过扩大决策者的风险态度和决策偏好,得出不同类型驾驶决策者在相同行驶环境下的不同交通流状态。这表明在实际道路交通中充分考虑驾驶决策者的心理并对其类型进行判断,可提升仿真模型的精度与可靠性。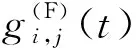

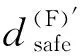

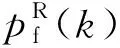
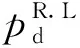
2.2 跟驰行为建模
3 数值模拟与仿真分析
3.1 仿真设置
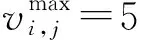
3.2 时空特性分析
3.3 换道分布特性分析
3.4 交通流特性分析
4 结论
