基于扩散滤波后正交分解的水下电场信号检测算法∗
2023-11-15甄国斌苏建业
甄国斌 刘 莎 崔 培 苏建业
(大连测控技术研究所 大连 116013)
1 引言
国外在水下隐身的技术上提升明显,仅靠传统的声学探测效果远不如前,所以目前迫切需要将更多的探测手段投入到应用中。电场信号探测在水下非声探测的领域中占有关键的地位,这些特征信号在浅海条件下相对更难隐蔽。
Ginzburg 在2002 年首次提出了基于正交基分解(OBF)的算法,可以在多种情况下帮助实现匹配滤波,后被广泛运用在磁异信号的检波流程中,本文拟将其思想运用到对水下电场信号的检测。OBF 分解算法被认为是高斯白噪声条件下对磁异信号处理的最优选择,但在实际情况下,非高斯白噪声导致算法的性能下降。所以在OBF分解前,可先进行预处理。选用扩散滤波对带噪信号做降噪处理,扩散滤波在信号梯度越大的地方扩散系数越小,使得自适应进行降噪的同时可以保护电场信号出现时的边缘特征,本文将选取合适的参数来控制低频电场信号的扩散滤波效果,再结合OBF分解提出一种新的电场信号检波算法,最后通过实际算例进行验证。
2 基于正交基分解的电磁信号检测算法
2.1 电偶极子模型
两个被距离无限小的导线∆l连接起来的电流源组成的系统被称为电偶极子[2]。电流I 与∆l 之间的关系为其中Mз被称为偶极子距。偶极子产生的电磁场含一个磁场分量Hφ和两个电场分量Er、Eθ,电场分量由Hφ求微分得到。求解矢量方程∇2H+k2H=0 得到:
其中σ是海水电导率,Mз为偶极子距。
2.2 OBF分解算法
磁异信号已被证明是由三组相互正交的基函数所构成,表示为下式[3]:
其中,μ0为真空磁导率,M 为磁矩,R0为目标位置信息,ai为基函数的权值,fi(w)是经过了施密特正交化算法后的标准正交基函数。fi(w)为已知参数所以在检波过程中可以直接求得权值a 并通过权值a进行门限判定。
将其推广至轴频电场信号的检测过程中,由三分量传感器收到的电场信号也是由三个相互正交的信号组成,分别是x 分量,y 分量,z 分量。根据电偶极子表达式,将静电场的正交模态信号表示为
其中w 表示目标的位置信息,fi(w)同样也是对三分量数据进行施密特正交化后的函数。
门限判决的关键步骤是求出ai,由于fi(w)相互正交,f1∗f1=1,f1∗f2=0,f1∗f3=0,对上式左右两边同时乘fi(w)后再积分可以得到ai的表达式:
在实际检测中,常使用滑动窗对离散数据进行卷积来达到实时检测的目的。
构造判决函数,E=,它的含义是信号S在正交分解后的能量,利用判决函数与设定的阈值进行比较,判断出是否检测到目标[6]。根据理想情况下仿真实验的归一化能量信号确定判决门限E′运用到实际检测中。综上,利用正交基分解进行检测的流程如图1。
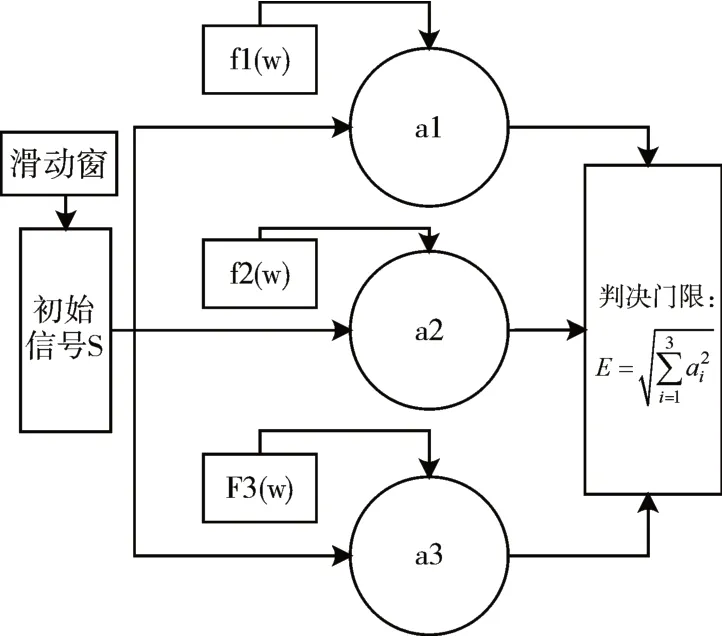
图1 正交基分解流程
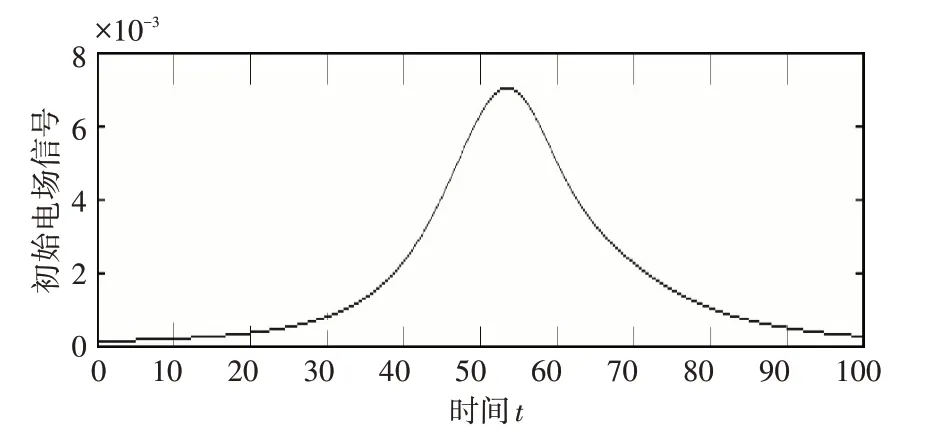
图2 初始电场信号
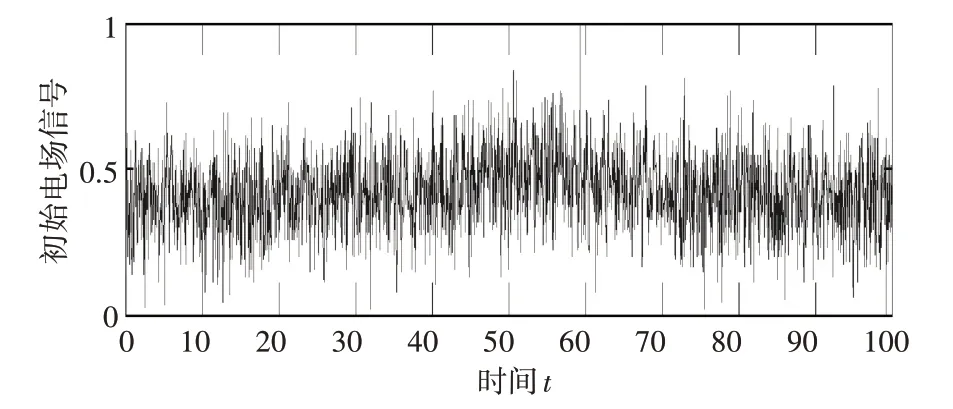
图3 含噪信号
3 基于扩散滤波的降噪算法
扩散方程在数学上应用了偏微分方程,迄今为止,信号和图像处理等技术领域中偏微分方程起到了越来越重要的作用,1990 年Perona 和Malik 把最初各向同性扩散方程中的常数扩散系数c 进化为关于梯度的单调非增函数,根据信号不同处的特征,把信号分成不同的区域,然后在区域内进行相同程度的扩散,在区域外不进行扩散,滤波模型拥有了自适应的去除噪声和保护信号边缘信息的功能[9]。
引入边缘检测算子|∇u|和新的扩散系数c(x,y,t)后的扩散方程如下:
其中u代表图像,∇表示梯度,div表示散度算子。c(x,y,t)有关于信号的梯度幅度值:
g(x)是需要进行定义的一个函数,一般采取两种形式:
或:
其中K>0,g(x)>=0,当x→∞的时候,g(x)趋近于0。K 是一个梯度阈值,当▽u 趋近于K 时,扩散过程逐渐停止;当▽u 大于K 时扩散过程还可以对边缘起到增强轮廓的作用,而当梯度阈值▽u 小于K时,起的作用与低通滤波器相同。g(x)的取值范围一般是在0~1 之间。作为一种局部自适应的扩散方法,加入了反馈的扩散系数c(x,y,t)因此可以达到在梯度变化小的地方进行扩散,为在梯度变化大的地方不进行扩散的效果。一般情况下,第一种形式降噪效果更明显,第二种形式对边缘的保护更好。
4 算法应用
1)首先在Matlab 中根据恒稳态电场公式画出电场信号曲线,之后的数据进行归一化处理。
2)加入-10dB 信噪比的高斯白噪声后,信号已经淹没在噪声中无法判别。
3)利用PM 扩散方程对带噪信号进行预处理,分别选取迭代次数为20次和300次,随着迭代次数的增加,波形越来越趋于平滑但是延迟时间会越来越大,综合考虑延迟时间、降噪效果和边缘信息,选取一个合适的参数。图4~5 降噪后已经出现趋近原信号的波形,预处理效果较好,信噪比得到一定改善。
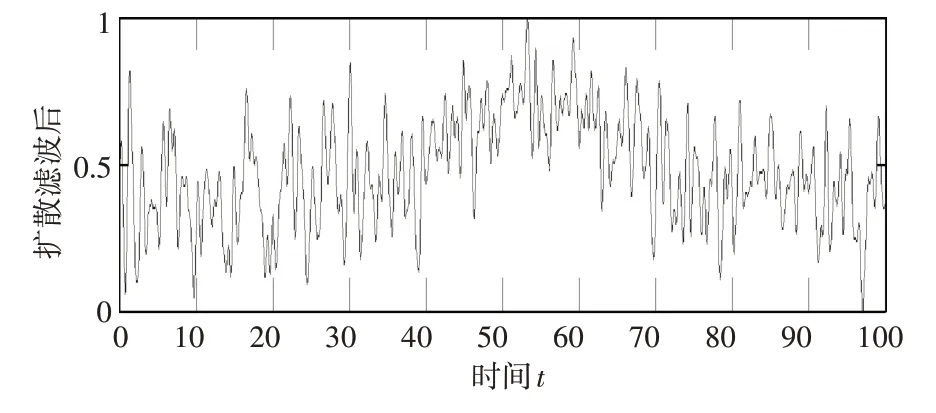
图4 迭代20次
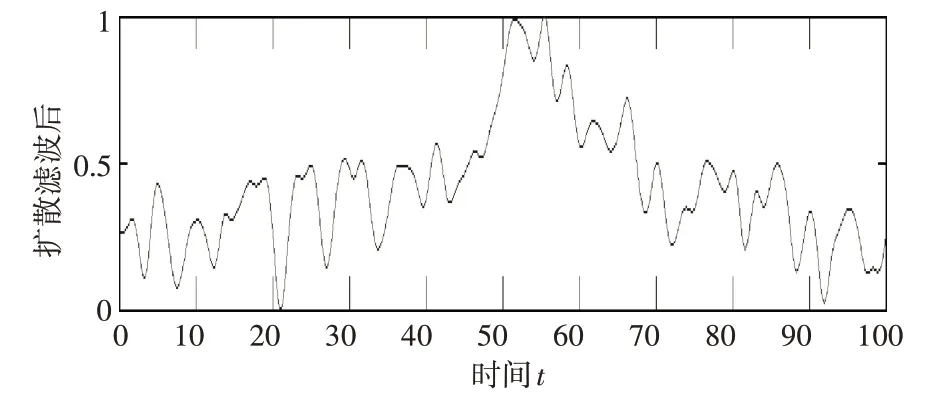
图5 迭代300次
4)对预处理后的信号进行正交基分解,求得归一化后的能量信号E 如图6。峰值时间出现在第54s,与初始信号相同,信噪比由-10dB 提升至约19.46dB,波形更加尖锐,在峰值附近的能量可以超过阈值,结果可以成功判断出电场信号。

图6 OBF分解
5 结语
本文提出的扩散滤波后正交基分解电场信号算法,通过扩散滤波预先滤除噪声,提升了信噪比,再通过正交基分解提取出能用于阈值检测的能量信号,经过仿真实验,成功判别出了电场信号。将正交基分解在磁探测中的优异性能延伸到电场领域,具有一定的实践意义。
